Министерство образования и науки Российской федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Тюменский государственный университет
Институт математики и компьютерных наук
Кафедра информатики и математики
КУРСОВАЯ РАБОТА
По дисциплине «Математический анализ»
на тему:
Дифференцирование в линейных нормированных пространствах
Выполнила: студентка 393 гр.
Жукова И.А.
Проверил: доцент кафедры МиИ
Салтанова Т.В.
Тюмень 2010
Оглавление
Введение
Основные понятия
Сильный дифференциал (дифференциал Фреше)
Слабый дифференциал (дифференциал Гато)
Формула конечных приращений
Связь между слабой и сильной дифференцируемостью
Дифференцируемые функционалы
Абстрактные функции
Интеграл
Производные высших порядков
Дифференциалы высших порядков
Формула Тейлора
Заключение1
Список литературы:
Введение
Функциональный анализ — разделматематики, в котором изучаются бесконечномерные пространства и их отображения.
Понятие нормированного пространства – одно из самых основных понятий функционального анализа. Теория нормированных пространств была построена, главным образом, С. Банахом в 20-х годах 20 века. Функциональный анализ за последние два десятилетия настолько разросся, настолько широко и глубоко проник почти во все области математики, что сейчас даже трудно определить самый предмет этой дисциплины. Однако в функциональном анализе есть несколько больших «традиционных» направлений, которые и поныне в значительной степени определяют его лицо. К их числу принадлежит дифференцирование линейных нормированных пространств.
Определение 1. Непустое множество 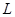 называется линейным пространством, если оно удовлетворяет следующим условиям: называется линейным пространством, если оно удовлетворяет следующим условиям:
Й. Для любых двух элементов 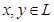 однозначно определен элемент однозначно определен элемент  , называемый их суммой, причем , называемый их суммой, причем
1. 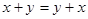 (коммутативность) (коммутативность)
2. 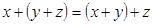 (ассоциативность) (ассоциативность)
В 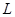 существует такой элемент 0, что существует такой элемент 0, что 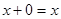 для всех для всех 
4. Для каждого  существует такой элемент существует такой элемент 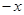 , что , что  . .
II. Для любого числа  и любого элемента и любого элемента  определен элемент определен элемент  , причем , причем
5. 
6. 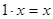
III. Операции сложения и умножения связаны между собой дистрибутивными законами:
7. 
8. 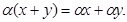
Определение 2. Линейное пространство  называется нормированным,
если на нем задана неотрицательная функция называется нормированным,
если на нем задана неотрицательная функция  , называемая нормой, удовлетворяющая условиям: , называемая нормой, удовлетворяющая условиям:
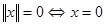

для любого  и любого числа и любого числа  ; ;
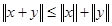
для любых 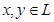 (неравенство треугольника). (неравенство треугольника).
Определение 3. Оператором называется отображение
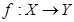 , ,
где 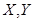 - это линейные пространства. - это линейные пространства.
Определение 4. Оператор 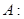  называется линейным, если для любых элементов называется линейным, если для любых элементов 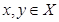 и любых чисел и любых чисел 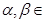 Rвыполняется равенство: Rвыполняется равенство:

Определение 5. Пусть 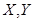 - линейные нормированные пространства, - линейные нормированные пространства,
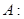  – линейный оператор, – линейный оператор,

Линейный оператор непрерывен в точке , если из того, что
, если из того, что
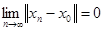 следует, что следует, что  . .
Определение 6. Линейный оператор 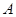 непрерывен, если он непрерывен в каждой точке непрерывен, если он непрерывен в каждой точке  . .
Определение 7. Линейный оператор называется ограниченным, если
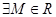 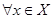 
Утверждение. Для линейного нормированного пространства непрерывность линейного оператора равносильна его ограниченности.
Определение8. Наименьшая из констант Mтаких, что  , называется нормой оператора А и обозначается , называется нормой оператора А и обозначается  . .
В частности, выполняется
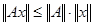
Справедливо следующее утверждение: для любого ограниченного линейного оператора
Пусть X и У — два нормированных пространства и F— отображение, действующее из X в Yи определенное на некотором открытом подмножестве О пространства X. Мы назовем это отображение дифференцируемым в данной точке , если существует такой ограниченный линейный оператор Lx , если существует такой ограниченный линейный оператор Lx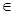 ж (X, Y),что для любого е> 0 можно найти д > 0, при котором из неравенства ||h||< д следует неравенство
ж (X, Y),что для любого е> 0 можно найти д > 0, при котором из неравенства ||h||< д следует неравенство
||F(x+ h)-F(x)-Lx
h||<е||h|| (1)
То же самое сокращенно записывают так:
А(ч + р)-А(ч)-Дч
р = щ(р)ю(2)
Из (I) следует, что дифференцируемое в точке х отображение непрерывно в этой точке. Выражение Lx
h(представляющее собой, очевидно, при каждом h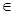 Xэлемент пространства У) называется сильным дифференциалом (или дифференциалом Фреше) отображения Fв точке х. Сам линейный оператор Lx
называется производной, точнее, сильной производной отображения Fв точке х. Мы будем обозначать эту производную символом F'(x). Xэлемент пространства У) называется сильным дифференциалом (или дифференциалом Фреше) отображения Fв точке х. Сам линейный оператор Lx
называется производной, точнее, сильной производной отображения Fв точке х. Мы будем обозначать эту производную символом F'(x).
Если отображение Fдифференцируемо в точке, то соответствующая производная определяется единственным образом. В самом деле, равенство
||L1
h— L2
h|| = o(h)для операторов
Li
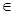 ж (X, У), i= 1, 2, ж (X, У), i= 1, 2,
возможно, лишь если L1
= L2
.
Установим теперь некоторые элементарные факты, непоcредственно вытекающие из определения производной.
Если F(x) = y0
= const, то F'(x) = О (т. е. F'(х)
в этом случае есть нулевой оператор).
Производная непрерывного линейного отображения Lесть само это отображение:
L'(x)=L(3)
Действительно, по определению имеем
L(x+ h)-L(x) = L(h).
3. (Производная сложной функции). Пусть X, У, Z— три нормированных пространства, U(x0)—окрестность точки х0
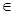 Х, F — отображение этой окрестности в У, у0
= F(x0
), V(yo
) — окрестность точки у0 Х, F — отображение этой окрестности в У, у0
= F(x0
), V(yo
) — окрестность точки у0
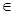 У и G— отображение этой окрестности в Z. Тогда, если отображение Fдифференцируемо в точке хо
, aGдифференцируемо в точке уо
, то отображение Н = GF(которое определено в некоторой окрестности точки х0
) дифференцируемо в точке хо
и У и G— отображение этой окрестности в Z. Тогда, если отображение Fдифференцируемо в точке хо
, aGдифференцируемо в точке уо
, то отображение Н = GF(которое определено в некоторой окрестности точки х0
) дифференцируемо в точке хо
и
H' (x0
)=G' (y0
)F' (x0
) (4)
Действительно, в силу сделанных предположений
А(ч0
+о) = А(ч0
) + Аэ (ч0
) о +о1
(о ) и
G(уо
+ з) = G(уо
) + G' (уо
) з + о2
(з).
НоF
'
(
x
0
)
иG
'(
yo
) —
ограниченные линейные операторы. Поэтому
H(х0
+ о) = G(уо
+ F' (x0
) о + о1
о ) = G(уо
) + G' (у0
) (F' (х0
) о + +о1
о)) +
+о2
(F' (x0
) о + о1
(о )) = G(у0
) + G' (уо) F' (х0
) о + о3
(о).
Если F, Gи Н — числовые функции, то формула (4) превращается в известное правило дифференцирования сложной функции.
4. Пусть Fи G— два непрерывных отображения, действующих из X в Y. Если Fи Gдифференцируемы в точке х0
, то и отображения F+ Gи aF(а — число) тоже дифференцируемы в этой точке, причем
(F+ G)'(х0
) = F'(х0
) + G'(х0
) (5)
(aF)'(x0
) = aF'(x0
).(6)
Действительно, из определения суммы операторов и произведения оператора на число сразу получаем, что
(F+G)(x0
+ h) = F(x0
+ h) + G(x0
+ h) = F(х0
) + G(х0
) + F' (х0
) h+
+G' (х0
) h+ o1
(h) и
aF (x0
+ h) = aF (x0
) + aF' (x0
) h + o2
(h),
откуда следуют равенства (5) и (6).
Слабый дифференциал (дифференциал Гато)
Пусть снова Fесть отображение, действующее из X в У. Слабым дифференциалом или дифференциалом Гато отображения Fв точке х (при приращении h)называется предел
DF(x,h)=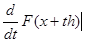 t
=0
= t
=0
= 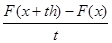  , ,
где сходимость понимается как сходимость по норме в пространстве У.
Иногда, следуя Лагранжу, выражение DF(x,h)называют первой вариацией отображения Fв точке х.
Слабый дифференциал DF(x,h)может и не быть линеен по h.Если же такая линейность имеет место, т. е. если
DF(х, h) = F'c
(х) h,
гдеF'c
(х) — ограниченный линейный оператор, то этот оператор называется слабой производной (или производной Гато).
Заметим, что для слабых производных теорема о дифференцировании сложной функции, вообще говоря, неверна.
Пусть О — открытое множество в X и пусть отрезок [х0
, х] целиком содержится в О. Пусть, наконец, Fесть отображение X в У, определенное на О и имеющее слабую производную F'c
в каждой точке отрезка [х0
, x]. Положив Дх = х — хо
и взяв произвольный функционал 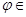 У*, рассмотрим числовую функцию У*, рассмотрим числовую функцию
f(t) = 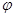 (F(x0
+tДх)), (F(x0
+tДх)),
определенную при 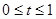 .Эта функция дифференцируема по t.Действительно, в выражении .Эта функция дифференцируема по t.Действительно, в выражении
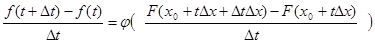
можно перейти к пределу под знаком непрерывного линейного функционала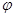 . В результате получаем . В результате получаем
F'(t) = 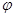 (F'c
(x0
+tДx) Дx) (F'c
(x0
+tДx) Дx)
Применив к функции fна отрезке [0, 1] формулу конечных приращений, получим
f(l) = f(0) + f'(и), где 0< и <1,
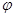 (F(x)-F(x0
))= (F(x)-F(x0
))= 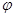 (F'c
(x0
+ и Дx) Дx)(7) (F'c
(x0
+ и Дx) Дx)(7)
Это равенство имеет место для любого функционала 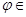 У* (величина и зависит, разумеется, от У* (величина и зависит, разумеется, от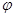 ).
Из (7) получаем ).
Из (7) получаем
|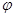 (F(x)-F(x0
))| (F(x)-F(x0
))|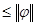   ||F'c
(x0
+ и Дx)|| ||F'c
(x0
+ и Дx)|| || Дx|| (8) || Дx|| (8)
Выберем теперь ненулевой функционал 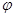 так, что так, что
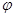 (F(х) - F(х0
)) = || (F(х) - F(х0
)) = ||
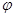 || ||
 ||
F(х) -
F(хо) || ||
F(х) -
F(хо) ||
(такой функционал 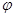 существует в силу следствия 4 теоремы Хана — Банаха (см. п. 3 § 1 гл. IV)). При этом из (8) получаем существует в силу следствия 4 теоремы Хана — Банаха (см. п. 3 § 1 гл. IV)). При этом из (8) получаем
||(F(х) - F(x)||  ||
F'c
(x0
+ и Дx)|| ||
F'c
(x0
+ и Дx)|| ||Дx|| (
Дx=
x
-
x
0
) (9) ||Дx|| (
Дx=
x
-
x
0
) (9)
Это неравенство можно рассматривать как аналог формулы конечных приращений для числовых функций. Применив формулу (9) к отображению
х —Ю А (х) — Аэс (хо
) Дч
получим следующее неравенство:
||F(x-F(хо
)
-F'c(хо
)
Дx||
  ||
F'c
(xo
+иДx)
-F'c
(x0
)|| ||
F'c
(xo
+иДx)
-F'c
(x0
)|| ||
Дx||
(10) ||
Дx||
(10)
Связь между слабой и сильной дифференцируемостью
Сильная и слабая дифференцируемость представляют собой различные понятия даже в случае конечномерных пространств. Действительно, из анализа хорошо известно, что для числовой функции
f(x) = f(x1,…,
xn
)
при n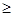 2 из существования производной 2 из существования производной
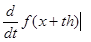
при любом фиксированном h= (f1,
...,fn
) еще не следует диф- ференцируемость этой функции, т. е. возможность представить ее приращение f(x+h)- f(x)в виде суммы линейной (по h) части и члена выше первого порядка малости относительно h.
Простейшим примером здесь может служить функция двух переменных
 (11) (11)
Эта функция непрерывна всюду на плоскости, включая точку (0,0). В точке (0,0) ее слабый дифференциал существует и равен 0, поскольку
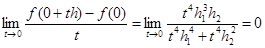
Вместе с тем этот дифференциал не является главной линейной частью приращения функции (11) в точке (0,0). Действительно, если положить h2
=h1
2
, то

Однако если отображение Fимеет сильную производную, то оно имеет и слабую, причем сильная и слабая производные совпадают. Действительно, для сильно дифференцируемого отображения имеем
А(ч + ер) — А (ч) = Аэ (ч) (ер) + о (ер) = еАэ (ч)р +о (ер) и
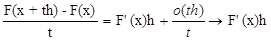
Выясним условия, при которых из слабой дифференцируемости отображения Fследует его сильная дифференцируемость.
Теорема 1. Если слабая производная F'c
(х) отображения Fсуществует в некоторой окрестности Uточки х0
и представляет собой в этой окрестности (операторную) функцию от х, непрерывную в x0
, то в точке x0
сильная производная F'(x0
) существует и совпадает со слабой.
Доказательство. По е>0 найдем д>0 так, чтобы при ||h||< д бвыполнялось неравенство:
|| F'c
(xo
+ h)-F'c
(xo
) ||  е е
Применив к отображению Fформулу (10), получим:
||
F(x0
+ h)-F(хо
) - F'c
(хо
) h||   ||F'c
(xo
+ иh)- F'c
(xo
)|| ||F'c
(xo
+ иh)- F'c
(xo
)||
||h|| е||h|| е||h||
Тем самым имеет место теорема 1, т. е. доказано как существование сильной производной F'(xо
), так и ее совпадение со слабой производной.
Дифференцируемые функционалы
Мы ввели дифференциал отображения F,действующего из одного нормированного пространства X в другое нормированное пространство У. Производная F'(х) такого отображения при каждом х — это линейный оператор из X в У, т. е. элемент пространства о(X, У). В частности, если У — числовая прямая, то F— принимающая числовые значения функция на X, т. е. функционал. При этом производная функционала Fв точке х0
есть линейный функционал (зависящий от х0
), т. е. элемент пространства X*.
Пример. Рассмотрим в действительном гильбертовом пространстве Н функционал F(x)= ||х||2
. Тогда
||x+ h||2
-||x||2
= 2(x, h) + || h||2
;
величина 2(x,h)представляет собой главную линейную (по h) часть этого выражения, следовательно,
F' (x) = F'c
(x) = 2х.
Абстрактные функции
Предположим теперь, что к числовой прямой сводится пространство аргументов X. Отображение F(x),сопоставляющее числу х элемент некоторого банахова пространства У, называется абстрактной функцией. Производная F'(х) абстрактной функции (если она существует) представляет собой (при каждом х) элемент пространства У — касательный вектор к кривой F(x).Для абстрактной функции (представляющей собой функцию одного числового аргумента) слабая дифференцируемость совпадает с сильной.
Интеграл
Пусть F— абстрактная функция действительного аргумента tсо значениями в банаховом пространстве У. Если Fзадана на отрезке [а, b], то можно определить интеграл функции Fпо отрезку [а,b]. Этот интеграл понимается как предел интегральных сумм
 , ,
отвечающих разбиениям
ф = е0
Бе1
Б ююю Бет
= иб ол
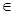 хел
бел+1
ъб хел
бел+1
ъб
при условии, что max(tk
+1
-tk
) 0. Интеграл (представляющий, собой, очевидно, элемент из Y) обозначается символом 0. Интеграл (представляющий, собой, очевидно, элемент из Y) обозначается символом
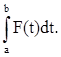
Рассуждения, в значительной мере аналогичные проводимым для функций, принимающих скалярные значения, показывают, что интеграл от функции, непрерывной на отрезке, существует; при этом он обладает свойствами обычного риманова интеграла.
Производные высших порядков
Пусть F— дифференцируемое отображение, действующее из X в У. Его производная F'(x)при каждом x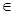 X
есть элемент из о (X, У), т. е. F'есть отображение пространства X в пространство линейных операторов о (Х, У). Если это отображение дифференцируемо, то его производная называется второй производной отображения Fи обозначается символом F".Таким образом, F"(x)есть элемент пространства о (Х, о (Х, У)) линейных операторов, действующих из X в о(X, У). Покажем, что элементы этого пространства допускают более удобную и наглядную интерпретацию в виде так называемых билинейных отображений. X
есть элемент из о (X, У), т. е. F'есть отображение пространства X в пространство линейных операторов о (Х, У). Если это отображение дифференцируемо, то его производная называется второй производной отображения Fи обозначается символом F".Таким образом, F"(x)есть элемент пространства о (Х, о (Х, У)) линейных операторов, действующих из X в о(X, У). Покажем, что элементы этого пространства допускают более удобную и наглядную интерпретацию в виде так называемых билинейных отображений.
Мы говорим, что задано билинейное отображение пространства X в пространство У, если каждой упорядоченной паре элементов х, х' из X поставлен в соответствие элемент у=В(х, х') 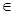 У так, что выполнены следующие условия:
У так, что выполнены следующие условия:
1. для любых  из X и любых чисел из X и любых чисел 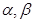 имеют место равенства: имеют место равенства:
В ( x1
+ x1
+ 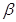 х2
, х2
,  ) = ) = В ( В (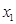 , ,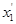 )+ )+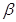 В (х2
, В (х2
, 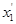 ), ),
В (x1
,   + +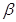 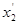 ) = ) =  В ( В (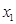 , ,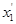 )+ )+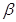 В(x1, В(x1,
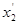 ); );
2. существует такое положительное число М, что
||В(х, х') ||  M||x|| M||x|| ||x’|| (17) ||x’|| (17)
при всех х, х'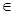 X. X.
Первое из этих условий означает, что отображение В линейно по каждому из двух своих аргументов; нетрудно показать, что второе условие равносильно непрерывности В по совокупности аргументов.
Наименьшее из чисел М, удовлетворяющих условию (17), называется нормой билинейного отображения В и обозначается ||В||.
Линейные операции над билинейными отображениями определяются обычным способом и обладают обычными свойствами.
Таким образом, билинейные отображения пространства X в пространство У сами образуют линейное нормированное пространство, которое мы обозначим В(Х2
, У). При полноте У полно и В(Х2
, У).
Каждому элементу А из пространства о(Х,о(Х,У)) можно поставить в соответствие элемент из В(Х2
, У), положив
В(х, х') = (Ах)х'.(18)
Очевидно, что это соответствие линейно. Покажем, что оно также и изометрично и отображает пространство о(X,о(Х,У)) на все пространство B(X2
,Y).Действительно, если у=В(х, х') = (Ах)х', то
||y|| ||Ax|| ||Ax|| ||x’|| ||x’|| ||A|| ||A|| ||x|| ||x|| ||x’||, ||x’||,
откуда
||B|| ||A||(19) ||A||(19)
С другой стороны, если задано билинейное отображение В, то при фиксированном x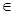 X
отображение X
отображение
х'→ (Ах)х' = В(х, х')
есть линейное отображение пространства X в У.
Таким образом, каждому x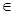 X
ставится в соответствие элемент Ах пространства о(X,У); очевидно, что Ах линейно зависит от х, т. е. билинейное отображение В определяет некоторый элемент А пространства о(Х, о(Х, У)). При этом ясно, что отображение В восстанавливается по А при помощи формулы (18) и X
ставится в соответствие элемент Ах пространства о(X,У); очевидно, что Ах линейно зависит от х, т. е. билинейное отображение В определяет некоторый элемент А пространства о(Х, о(Х, У)). При этом ясно, что отображение В восстанавливается по А при помощи формулы (18) и
||Ах||= 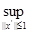 ||(Ax)x'||= ||(Ax)x'||=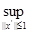 ||В(х,x') ||В(х,x')  ||B|| ||B|| ||x||, ||x||,
Откуда
||A|| ||B||(20) ||B||(20)
Сопоставляя (19) и (20), получаем||A|| = ||В||. Итак, соответствие между B(X2
,Y)и о{X, о(X,Y)), определяемое равенством (18), линейно и изометрично, а следовательно, взаимно однозначно. При этом образ пространства о(Х, о(Х, У)) есть все В(Х2
, У).
Мы выяснили, что вторая производная F"(x)есть элемент пространства о(X, о (X, У)). В соответствии с только что сказанным мы можем считать F"(x)элементом пространства В(Х2
, Y).
Очевидным образом можно ввести понятие третьей, четвертой и вообще п-й производной отображения F,действующего из X в Y,определив п-ю производную как производную от производной (п—1)-го порядка. При этом, очевидно, п-я производная представляет собой элемент пространства о(Х, о(Х, ..., о(X, У))). Повторяя рассуждения, проведенные для второй производной, можно каждому элементу этого пространства естественным образом поставить в соответствие элемент пространства N(Хп
, У)
n-линейных отображений X в У.
При этом под n-линейным отображением понимается такое соответствие y=N(x', х", ...,x(
n
)
) между упорядоченными системами (х', х", .. . , x(
n
)
) элементов из X и элементами пространства У, которое линейно по каждому из хi
при фиксированных остальных элементах и удовлетворяет при некотором М > 0 условию
|| N (x', х", ..., x(
n
)
) || М || х' || • || х" || ... || x(
n
)
||. М || х' || • || х" || ... || x(
n
)
||.
Таким образом, п-ю производную отображения Fможно считать, элементом пространства N(Xn
,У).
Дифференциалы высших порядков
Мы определили (сильный) дифференциал отображения Fкак результат применения к элементу h Х линейного оператора F'(x),т. е.
Х линейного оператора F'(x),т. е.
dF= F'(x)h
Дифференциал второго порядка определяется как
d2
F= F" (х)(h, h),
т. е. как квадратичное выражение, отвечающее отображению
F''(х) В(X2
, У)
В(X2
, У)
Аналогично дифференциалом п-го порядка называется
dn
F=F(
n
)
(x)(h,h,h),
т. е. тот элемент пространства У, в который элемент (h, h, ..., h)  переводится отображением F
(
n
)
(x).
переводится отображением F
(
n
)
(x).
Формула Тейлора
Сильная дифференцируемость отображения Fозначает, что разность
F(x+h)—F(x)
может быть представлена в виде суммы линейного члена и слагаемого, имеющего порядок выше первого относительно ||h||. Обобщением этого факта является формула, аналогичная формуле Тейлора для числовых функций.
Теорема 2. Пусть F— отображение, действующее из X в У, определенное в некоторой области О X и такое, что F(
n
)
(x) существует и представляет собой равномерно непрерывную функцию от х в О. Тогда имеет место равенство X и такое, что F(
n
)
(x) существует и представляет собой равномерно непрерывную функцию от х в О. Тогда имеет место равенство
f(x + h)-F(x) = F'(x)h +  F"(x)(h, h)+ ... F"(x)(h, h)+ ...
... +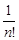 F(
n
)
(x)(h,…,h) + щ (х, h), (21) F(
n
)
(x)(h,…,h) + щ (х, h), (21)
где
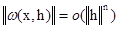
Доказательство будем вести по индукции. При n= 1 равенство (21) тривиально. Возьмем теперь произвольное фиксированное nи предположим, что равенство, получающееся из (21) заменой nна n-1, уже доказано для всех отображений, удовлетворяющих условиям теоремы, в которых nзаменено на п-1. Тогда для отображения F'имеем
F'(x+ h) = F'(x) + F"(x)h+ F"'(x)(h,h) + ... F"'(x)(h,h) + ...
… + 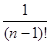 F(
n
)
(x)(h,…,h) + щ1
(х, h), (22) F(
n
)
(x)(h,…,h) + щ1
(х, h), (22)
где
||щ1
(х, h)|| = o(||h||n
-1
)
Интегрируя обе части равенства (22) по отрезку [х, x+h] и пользуясь формулой Ньютона — Лейбница (15), мы получим

 , (21) , (21)
Где
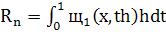 . .
из (23) получаем
А(ч+ р)-А (х)= Аэ(ч)р +  АЭ(ч)(рбр)+ ююю АЭ(ч)(рбр)+ ююю
…+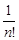 F(
n
)
(x)(h,…,h) + Rn
, причем F(
n
)
(x)(h,…,h) + Rn
, причем
||Rn
|| 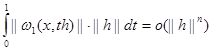
Тем самым наше утверждение доказано.
Формулу (21) называют формулой Тейлора для отображений.
Заключение
В этой работе представлены некоторые первоначальные понятия , относящиеся к нелинейному функциональному анализу, в основном к теории дифференцирования, и некоторые применения этих понятий.
Некоторые задачи, возникающие в функциональном анализе, носят существенно нелинейный характер; они приводят к необходимости развивать наряду с «линейными» и « нелинейными» функциональный анализ, т.е изучать нелинейные функционалы и нелинейные операторы в бесконечномерных пространствах.
К нелинейному функциональному анализу относится, по существу, такая классическая область математики, как вариационное исчисление, основы которого были заложены еще в XVII-XVIIIвв. в работах Бернулли, Эйлера, Лагранжа. Однако в целом нелинейный функциональный анализ представляет собой сравнительно новую область математики, пока еще далекую от своего завершения.
1. Колмогоров А.Н., Фомин С.В. - Элементы теории функций и функционального анализа. М., Наука, 1981. – 475 с.
2. Шилов Г.Е. – Дифференцирование функций в линейном пространстве. Ярославль, 1978. – 118стр.
3. Банах С. – Дифференциальное и интегральное исчисление. М.,Наука, 1972. – 424стр.
|