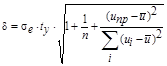Контрольная работа: Свойства линейной прогрессии
|
Название: Свойства линейной прогрессии Раздел: Рефераты по экономико-математическому моделированию Тип: контрольная работа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Министерство образования и науки Украины Донбасская государственная машиностроительная академия Контрольная работа по дисциплине: «Эконометрика» Выполнила: студентка гр. ПВ 09-1з Бурденюк Е.Н. Проверила: Гетьман И. Краматорск 2010 1. Теоретический вопрос Свойства линейной прогрессии 1. Прямая регрессии всегда проходит через центр рассеивания корреляционного поля, т.е. через точку ( 2. Из выражения Если rxy >0, то b1 >0, a острый, связь между х и у – прямая, т.е. с ростом х у возрастает. Если rxy <0, то b1 <0, a тупой связь между х и у обратная. 2. ЗадачаНайдите коэффициент эластичности для указанной модели в заданной точке x. Сделать экономический вывод.
X=2 1. Найдем производную функции 2. Найдем эластичность 3. Коэффициент эластичности для точки прогноза: X=2
Коэффициент эластичности показывает, что при изменении фактора X =2 на 1% показатель Y увеличивается на 5%. 3. Задача Для представленных данных выполнить следующее задание: 1. Провести эконометрический анализ линейной зависимости показателя от первого фактора. Сделать прогноз для любой точки из области прогноза, построить доверительную область. Найти коэффициент эластичности в точке прогноза. 2. Провести эконометрический анализ нелинейной зависимости показателя от второго фактора, воспользовавшись подсказкой. Сделать прогноз для любой точки из области прогноза, построить доверительную область. Найти коэффициент эластичности в точке прогноза. 3. Провести эконометрический анализ линейной зависимости показателя от двух факторов. Сделать точечный прогноз для любой точки из области прогноза. Найти частичные коэффициенты эластичности в точке прогноза. Производительность труда, фондоотдача и уровень рентабельности по плодоовощным консервным заводам области за год характеризуются следующими данными:
Нелинейную зависимость принять Обозначим производительность труда (грн) – Х, уровень рентабельности (%) – У. Построим линейную зависимость показателя от фактора. Найдем основные числовые характеристики. Объем выборки n=15 – суммарное количество наблюдений. Минимальное значение Х=2827, максимальное значение Х=7321, значит, производительность труда изменяется от 2827 до 7321 грн. Минимальное значение У=10.9, максимальное значение У=28.3, уровень рентабельности изменяется от 10.9 до 28.3%. Среднее значение
После того, как была построена модель, необходимо проверить ее на адекватность. Для анализа общего качества оцененной линейной регрессии найдем коэффициент детерминации: Проверим с помощью критерия Фишера. Для проверки найдем величины: Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза: Найдем полуширину доверительного интервала в каждой точке выборки xпр :
sе
– средне квадратичное отклонение выборочных точек от линии регрессии ty = критическая точка распределения Стьюдента для надежности g=0,9 и k2 =13. n =15.
или xпр – точка из области прогнозов. Прогнозируемый доверительный интервал для любого х такой Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область. Т.е. при производительности труда 5000 грн уровень рентабельности составит от 14% до 25%. Найдем эластичность. Для линейной модели
Коэффициент эластичности показывает, что при изменении х=5000 на 1% показатель y увеличивается на 0,996%. Обозначим фондоотдачу – Х, уровень рентабельности – У. Построим нелинейную зависимость показателя от фактора вида Минимальное значение Х=25.3, максимальное значение Х=49.3, значит, фондоотдача изменяется от 25.3 до 49.3грн. Минимальное значение У=10.9, максимальное значение У=28.3, уровень рентабельности изменяется от 10.9 до 28.3%. Среднее значение Дисперсия Среднеквадратическое отклонение Определим, связаны ли Х и У между собой, и, если да, то определить формулу связи. По таблице строим корреляционное поле (диаграмму рассеивания) – нанесем точки Точка с координатами По виду корреляционного поля можно предположить, что зависимость между y и x нелинейная. Пытаемся описать связь между х и у зависимостью Проверим тесноту линейной связи u и v. Найдем коэффициент корреляции: Параметры b0,
b1
находим по МНК. Проверим значимость коэффициентов bi . Значимость коэффициента b может быть проверена с помощью критерия Стьюдента:
Получили линейную модель После того, как была построена модель, необходимо проверить ее на адекватность. Для анализа общего качества оцененной линейной регрессии найдем коэффициент детерминации: Проверим с помощью критерия Фишера. Для проверки находим величины: Так как линейная модель адекватна, то и соответствующая нелинейная модель тоже адекватна. Находим параметры исходной нелинейной модели: а=b1 =-3,45; b = b0 =4,53. Вид нелинейной функции: Т.е. зависимость уровня рентабельности от фондоотдачи имеет вид: Найдем прогноз на основании модели. Выберем произвольную точку из области прогноза [25.3; 49.3], х=1 Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза: Найдем полуширину доверительного интервала в каждой точке выборки. Для этого найдем полуширину для линейной модели:
sе
– средне квадратичное отклонение выборочных точек от линии регрессии
uпр
– точка из области прогнозов. Прогнозируемый доверительный интервал для любого u такой Для нелинейной модели найдем доверительный интервал, воспользовавшись обратной заменой: Прогноз для х=1 составит от 5,31 до 22,58 с гарантией 90%. Т.е. при фондоотдаче 1 грн. уровень рентабельности составит от 5.31% до 22.58%. Найдем эластичность.
где Коэффициент эластичности для точки прогноза:
Коэффициент эластичности для точки прогноза:
Коэффициент эластичности показывает, что при изменении фондоотдачи 1 грн. на 1% уровень рентабельности увеличивается на 1.57%. Обозначим производительность труда – Х1 грн., фондоотдачу - Х2 грн, уровень рентабельности – У %. Построим линейную зависимость показателя от факторов. Найдем основные числовые характеристики. Объем выборки n=15 – суммарное количество наблюдений. Минимальное значение Х1=2827, максимальное значение Х1=7321, значит, производительность труда изменяется от 2827 до 7321грн. Минимальное значение Х2=25.3, максимальное значение Х2=49.3, значит, фондоотдача изменяется от 25.3 до 49.3грн. Минимальное значение У=10.9, максимальное значение У=28.3, уровень рентабельности изменяется от 10.9 до 28.3%. Среднее значение
Среднее значение производительности труда составляет 4862,87 грн, среднее значение фондоотдачи составляет 38.4 грн., среднее значение уровня рентабельности составляет 18.93%. Дисперсия Среднеквадратическое отклонение Прежде чем строить модель, проверим факторы на коллинеарность. По исходным данным cтроим корреляционную матрицу. Коэффициент корреляции между X1
и X2
равен 0,88. Так как Определим, связаны ли Х1, Х2 и У между собой. Для определения тесноты линейной связи найдем коэффициент корреляции
: r=
0,898. Так как Пытаемся описать связь между х и у зависимостью Параметры b0,
b1
,b2
находим по МНК. Проверим значимость коэффициентов bi . Значимость коэффициента b может быть проверена с помощью критерия Стьюдента:
Проверим адекватность. Для анализа общего качества оцененной линейной регрессии найдем коэффициент детерминации: Проверим с помощью критерия Фишера. Для проверки найдем величины: Получили модель зависимости уровня рентабельности плодоовощным консервным заводам области от производительности труда и фондоотдачи Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза: Т.е. при производительности труда 5000 грн и фондоотдаче 1 грн уровень рентабельности составит 19.84%. Найдем эластичность по каждому фактору. Для линейной модели
Коэффициент эластичности показывает, что увеличении производительности труда с 5000 грн. на 1% и при фондоотдаче 30 грн., уровень рентабельности увеличится с 19.84 грн на 1.05%. Для линейной модели
Коэффициент эластичности показывает, что при производительности труда 5000 грн. и увеличении удельного фондоотдачи с 30грн. на 1%, уровень рентабельности уменьшится с 19.84 грн на 0,06%. Для увеличения рентабельности заводов целесообразней увеличивать производительность труда при неизменной фондоотдаче. Использованная литература 1. Экономико-математические методы и прикладные модели: Учебное пособие для вузов / В.В. Федосеев, А.Н. Гармаш и др. - М.: ЮНИТИ, 1999. - 391 с. 2. Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL. Практикум: Учебное пособие для вузов. - М.: Финстатинформ, 2000.- 136 с. 3. Компьютерные технологии экономико-математического моделирования: Учебное пособие для вузов / Д.М. Дайитбегов, И.В. Орлова. - М.: ЮНИТИ, 2001. 4. Эконометрика: Учебник / Под ред. И.И. Елисеевой. - М.: Финансы и статистика, 2001. 5. Практикум по эконометрике: Учебное пособие / Под ред. И.И. Елисеевой - М.: Финансы и статистика, 2001. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
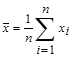 . Среднее значение производительности труда составляет 4790,53 грн, среднее значение уровня рентабельности составляет 19.41%. Дисперсия
. Среднее значение производительности труда составляет 4790,53 грн, среднее значение уровня рентабельности составляет 19.41%. Дисперсия  =0,9 Так как
=0,9 Так как