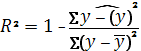Контрольная работа: Составление и решение уравнений линейной регрессии
|
Название: Составление и решение уравнений линейной регрессии Раздел: Рефераты по экономико-математическому моделированию Тип: контрольная работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ КАФЕДРА ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ КОНТРОЛЬНАЯ РАБОТА по дисциплине Эконометрика Липецк 2009 Задача 1 По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции ( Требуется: 1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии. 2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 3. Проверить выполнение предпосылок МНК. 4. Осуществить проверку значимости параметров уравнения регрессии с помощью t‑критерия Стьюдента 5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью 6. Осуществить прогнозирование среднего значения показателя 7. Представить графически: фактические и модельные значения 8. Составить уравнения нелинейной регрессии: · гиперболической; · степенной; · показательной. Привести графики построенных уравнений регрессии. 9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.
Решение 1. Уравнение линейной регрессии имеет вид: y = a + b * x . Данные, используемые для расчета параметров a иb линейной модели, представлены в табл. 1: Таблица 1
Уравнение линейной регрессии имеет вид: у= 11,78+0,76х С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличится в среднем на 76 тыс. руб. Это свидетельствует об эффективности работы предприятия. 2. Вычисленные остатки и остаточная сумма квадратов представлены в таблице 1. Дисперсию остатков
Рисунок 1 3. Проверим выполнение предпосылок МНК на основе анализа остаточной компоненты (см. табл. 1). Независимость остатков проверяется с помощью критерия Дарбина – Уотсона по формуле Для обнаружения гетероскедастичности используем тест Голдфельда – Квандта: 1) Упорядочим наблюдения по мере возрастания переменной х. 2) Разделим совокупность на 2 группы по 5 наблюдений и для каждой определим уравнение регрессии. Воспользуемся инструментом Регрессия пакета Анализ данных, полученные результаты представлены в табл. 2. Таблица 2
3) Определим остаточную сумму квадратов для первой 4) Вычислим отношение 4. Проверим значимость параметров уравнения регрессии с помощью t‑критерия Стьюдента
Рисунок 2 Табличное значение t‑критерия Стьюдента 2,30. tрасч =6,92, так как tрасч >tтабл , то коэффициент а1 значим. 5. Значение коэффициента детерминации (R – квадрат) можно найти в таблице Регрессионная статистика (рис. 2). Коэффициент детерминации/ Он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 85,7% вариации зависимой переменной (объем выпуска продукции) учтено в модели и обусловлено влиянием включенного фактора (объем капиталовложений). Значение F– критерия Фишера можно найти в таблице протокола Excel (рис. 2), Fрасч =47,83. Табличное значение F– критерия при доверительной вероятности 0,05 равно 4,46, т. к. Fрасч >Fтабл , уравнение регрессии следует признать адекватным. Определим среднюю относительную ошибку аппроксимации? в среднем расчетные значения у для линейной модели отличаются от фактических на 1% – хорошее качество модели. 6. Осуществим прогнозирование среднего значения показателя Модель зависимости объема выпуска продукции от величины капиталовложений у= 11,78+0,76х. Для того чтобы определить среднее значение фактора У при 80% максимального значения фактора Х, необходимо подставить Хпрогн =Хmax *0,8=22*0,8=17,6 в полученную модель: Упрогн =11,78+0,76*17,6=25,17 Для построения интервального прогноза рассчитаем доверительный интервал. Критерий Стьюдента (при v=n -2=10–2=8) равен 1,8595. Ширину доверительного интервала вычислим по формуле:
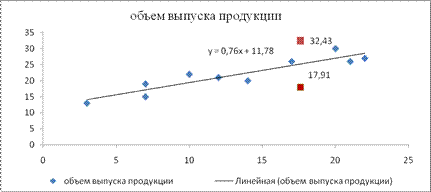
таким образом, прогнозное значение будет находиться между: Yпрогн(80 % max ) += 25,17+7,26=32,43 – верхняя граница прогноза, Yпрогн(80 % max ) – =25,17–7,26=17,91 – нижняя граница прогноза. 7. Графическое представление (рис. 3) модели парной регрессии зависимости объема выпуска продукции от объема капиталовложений: фактические и модельные значения
Рисунок 3 8. Уравнение гиперболической функции: y = a + b / x . Произведем линеаризацию путем замены Х=1/х . В результате получим линейное уравнение y = a + b Х. Рассчитаем его параметры по данным таблицы 3 Таблица 3
получим следующее уравнение гиперболической модели: ỹ =27,38–50,97/х . Уравнение степенной модели имеет вид: у=а*х b . Для линеаризации переменных произведем логарифмирование обеих частей уравнения: lgy=lg a +blgx . Обозначим Y=lgy', X=lgx, A=lga . Тогда уравнение примет вид Y=A+bX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные табл. 4: Таблица 4
Уравнение регрессии будет иметь вид: У=0,9103+0,3938*Х. Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения: ỹ=100,9103 *х0,3938 . Получим уравнение степенной модели регрессии: ỹ=8,1339*х0,3938 . Уравнение показательной кривой: ỹ=а*bx . Осуществим логарифмирование обеих частей уравнения: lgy=lg a +x*lgb . Обозначим Y=lgy', В=lgb, A=lga. Получим линейное уравнение регрессии: Y=A+Вх . Рассчитаем его параметры, используя данные табл. 5 Таблица 5
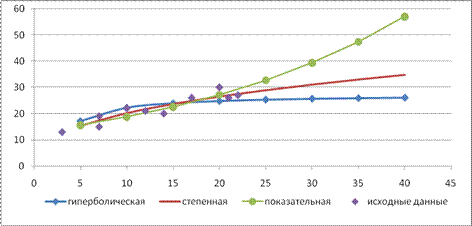
Уравнение имеет вид: У=1,11+0,0161х . Перейдем к исходным переменным х и у , выполнив потенцирование уравнения: ỹ =101,11 (10 0,0161 )х , ỹ =12,99*1,038х – уравнение показательной кривой. Графики построенных уравнений регрессии приведены на рис. 4.
Рисунок 4 9. Коэффициент детерминации: Для сравнения и выбора лучшей модели строим сводную таблицу результатов (табл. 6). Таблица 6
Вывод: на основании полученных данных лучшей является степенная модель регрессии, т. к. она имеет наибольший коэффициент детерминации R2 =0,862, т.е. вариация факторного признака У (объем выпуска продукции) на 86,2% объясняется вариацией фактора Х (объемом капиталовложений), и наименьшую относительную ошибку (в среднем расчетные значения для степенной модели отличаются от фактических данных на 0,034%). Также степенная модель имеет наибольший коэффициент эластичности, т.е. при изменении фактора на 1% зависимая переменная изменится на 0,24%, таким образом степенную модель можно взять в качестве лучшей для построения прогноза. Задача 2а и 2б Имеются два варианта структурной формы модели, заданные в виде матриц коэффициентов модели. Необходимо для каждой матрицы записать системы одновременных уравнений и проверить их на идентифицируемость. Задача 2а Решение. Запишем систему одновременных уравнений: у1= b 12 у2+ b 13 у3+ a 12 х2+ a 13 х3 у2= b 23 у3+ a 21 х1+ a 22 х2+ a 24 x4 у3 = b 32 у2+ a 31 х1+ a 32 х2+ a 33 х3 Проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации. 1) В первом уравнении три эндогенные переменные у1, у2, у3 (Н=3). В нем отсутствуют экзогенные переменные х1, х4 (D=2). Необходимое условие идентификации D+1=H, 2+1=3 выполнено. Для проверки на достаточное условие составим матрицу из коэффициентов при переменных х1 и х4 (табл. 7) Таблица 7
Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, первое уравнение идентифицируемо. 2) Во втором уравнении две эндогенные переменные у2, у3 (Н=2). В нем отсутствует экзогенная переменная х3 (D=1). Необходимое условие идентификации D+1=H, 1+1=2 выполнено. Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у1 и х3 (табл. 8) Таблица 8
Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, второе уравнение идентифицируемо. 3) В третьем уравнении две эндогенные переменные у2, у3 (Н=2). В нем отсутствует экзогенная переменная х4 (D=1). Необходимое условие идентификации D+1=H, 1+1=2 выполнено. Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у1 и х4 (табл. 9) Таблица 9
Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, третье уравнение идентифицируемо. Вывод: все уравнения системы идентифицируемы, систему можно решать. Задача 2б Решение Запишем систему уравнений: у1= b 13 у3+ a 11 х1+ a 13 х3+ a 14 х4 у2= b 21 у1+ b 23 у3+ a 22 х2+ a 24 х4 у3= b 31 у1+ a 31 х1+ a 33 х3+ a 34 х4 Проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации. 1) В первом уравнении две эндогенные переменные у1, у3 (Н=2). В нем отсутствует экзогенная переменная х2 (D=1). Необходимое условие идентификации D+1=H, 1+1=2 выполнено. Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у2 и х2 (табл. 10) Таблица 10
Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, первое уравнение идентифицируемо. 2) Во втором уравнении три эндогенные переменные у1, у2, у3 (Н=3). В нем отсутствуют экзогенные переменные х1, х3 (D=2). Необходимое условие идентификации D+1=H, 2+1=3 выполнено. Для проверки на достаточное условие составим матрицу из коэффициентов при переменных х1 и х3 (табл. 11) Таблица 11
Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, первое уравнение идентифицируемо. 3) В третьем уравнении две эндогенные переменные у1, у3 (Н=2). В нем отсутствует экзогенная переменная х2 (D=2). Необходимое условие идентификации D+1=H, 1+1=2 выполнено. Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у2 и х2 (табл. 12) Таблица 12
Определитель матрицы равен нулю (первая строка состоит из нулей). Значит, достаточное условие не выполнено, и третье уравнение нельзя считать идентифицируемым. Вывод: не все уравнения системы идентифицируемы, систему решать нельзя. Задача 2в По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов (КМНК), построить структурную форму модели вида: y1= a01 + b12 y2 + a11 x1 + e 1 y2= a02 + b21 y1 + a22 x2 + e 2
Решение Для построения модели мы располагаем информацией, представленной в табл. 13. Таблица 13. Фактические данные для построения модели
Структурная форма модели преобразуется в приведенную форму: у1= d 11 x 1+ d 12 x 2+ u 1 y 2= d 21 x 1+ d 22 x 2+ u 2 , где u1 и u2 – случайные ошибки. Для каждого уравнения приведенной формы при расчете коэффициентов d можно применить МНК. Для упрощения расчетов можно работать с отклонениями от средних уровней у=у-уср и х=х-хср . Преобразованные таким образом данные табл. 13 сведены в табл. 14. Здесь же показаны промежуточные рассчеты, необходимые для определения коэффициентов d . Таблица 14
Для нахождения коэффициентов первого приведенного уравнения можно использовать систему нормальных уравнений: Σу1 х1 =d11 Σx 1 2 + d 12 Σx 1 x 2 ; Σy 1 x 2 = d 11 Σx 1 x 2 + d 12 Σx 2 2 . Подставляя рассчитанные в табл. 14 значения сумм, получим: 174,333= 47,333d11 +28,333 d 12 471,333=28,333 d 11 +191,333 d 12 . Решение этих уравнений дает значения d11 =2,423, d12 =2,105. Первое уравнение приведенной формы примет вид: у1 =2,423х1 +2,105х2 + u 1 . Для нахождения коэффициентов второго приведенного уравнения можно использовать систему нормальных уравнений: Σу2 х1 =d21 Σx 1 2 + d 22 Σx 1 x 2 Σy 2 x 2 = d 21 Σx 1 x 2 + d 22 Σx 2 2 Подставляя рассчитанные в табл. 14 значения сумм, получим: 131,267=47,333d21 +28,333 d 22 360,767=28,333 d 21 +191,333 d 22 . Решение этих уравнений дает значения d21 =1,805, d22 =1,618. Второе уравнение приведенной формы примет вид: у2 =1,805х1 +1,618х2 + u 2 Для перехода от приведенной формы к структурной форме модели найдем х2 из второго уравнения приведенной модели: х2 =(у2 -1,805х1 )/1,618 . Подставив это выражение в первое уравнение приведенной модели, найдем структурное уравнение: у1 =2,423х1 +2,105 (у2 -1,805х1 )/1,618 =2,423х1 +1,3у2 -1,115х1 =1,3у2 +1,308х1 Таким образом, b 12 =1,3 а11 =1,308 . Найдем х1 из первого уравнения у1 =2,423х1 +2,105х2 приведенной формы: х1 =(у1 -2,105х2 )/2,423 Подставив это выражение во второе уравнение приведенной модели, найдем структурное уравнение: у2 =1,805 (у1 -2,105х2 )/2,423+1,618х2 =0,745 у1 -0,868х2 +1,618х2 =0,745у1 +0,75х2 Таким образом, b 21 = 0,745 а22 =0,75 Свободные члены структурной формы находим из уравнений: А01 =у1,ср -b12 у2,ср -а11 х1,ср =58,77 – 1,3*29,53–1,308*5,67=14,04 А02 =у2,ср -b21 у1,ср -а22 х2,ср =29,53–0,745*58,77–0,75*9,67=-5,83 Окончательный вид структурной модели: y1= a01 + b12 y2 + a11 x1 + e 1 = 14,04+1,3у2 +1,308х1 +e 1 ; y2= a02 + b21 y1 + a22 x2 + e 2 = -5,83+0,745у1 +0,75х2 + e 2 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
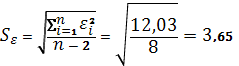 –
стандартная ошибка оценки.Построим график остатков (рис. 1)
–
стандартная ошибка оценки.Построим график остатков (рис. 1)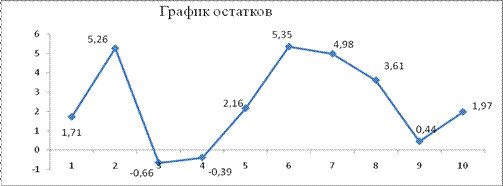
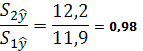 , т. к. Fнабл
=0,98, Fкр(α,к1,к2)
= Fкр(0,05,5,5)
=5,05 (из таблицы критерия Фишера), Fнабл
<Fкр,
то гетероскедастичность отсутствует, предпосылка о равенстве дисперсий остаточных величии не нарушена.
, т. к. Fнабл
=0,98, Fкр(α,к1,к2)
= Fкр(0,05,5,5)
=5,05 (из таблицы критерия Фишера), Fнабл
<Fкр,
то гетероскедастичность отсутствует, предпосылка о равенстве дисперсий остаточных величии не нарушена.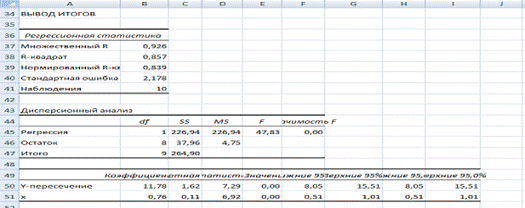
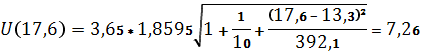 ,
,