Сліди і базиси розширеного поля. Подання точок кривоїу різних координатних системах. Складність арифметичних операцій у групах точок ЕК
Від ідеї створення криптосистем на еліптичних кривих ( ) до сьогоднішнього дня поряд із криптоаналізом цих систем фахівці безупинно і плідно працюють над підвищенням ефективності ) до сьогоднішнього дня поряд із криптоаналізом цих систем фахівці безупинно і плідно працюють над підвищенням ефективності  . .
Насамперед це відноситься до швидкодії криптосистеми або швидкості обчислень. Одним з напрямків робіт у цій сфері було вивчення і порівняльний аналіз арифметики в поліноміальному і нормальному базисах поля  . .
1. Сліди і базиси розширеного поля
Операції в розширених полях вимагають введення таких понять, як слід елемента поля та базису поля.
Нехай  - просте поле і - просте поле і  - його розширення. - його розширення.
Слідом елемента 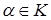 над полем над полем  називається сума сполучених елементів поля називається сума сполучених елементів поля 
 . .
Зокрема, слід елемента над полем 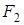 визначається сумою визначається сумою
 . .
Розширення поля Галуа 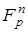 є є  -вимірним векторним простором над полем -вимірним векторним простором над полем  . Базисом цього поля називається будь-яка множина з . Базисом цього поля називається будь-яка множина з  лінійно незалежних елементів поля лінійно незалежних елементів поля  (див. лекції з дисципліни РПЕК). Кожен елемент поля подається (див. лекції з дисципліни РПЕК). Кожен елемент поля подається  -вимірним вектором з координатами з поля -вимірним вектором з координатами з поля  (або поліномом степеня (або поліномом степеня 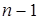 з коефіцієнтами з з коефіцієнтами з  ). Його також можна виразити як лінійну комбінацію векторів базису. ). Його також можна виразити як лінійну комбінацію векторів базису.
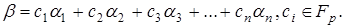
Теорема 1.
Елементи  поля поля 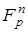 утворюють базис над полем утворюють базис над полем  тоді і тільки тоді, коли визначник матриці Вандермонда тоді і тільки тоді, коли визначник матриці Вандермонда

або визначник
 
Із множини всіляких базисів найбільш розповсюдженими є поліноміальний і нормальний базиси поля 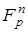 . .
Поліноміальний базис, звичайно, будується за допомогою послідовних степенів примітивного елемента поля  . Його назва пов'язана з тим, що при . Його назва пов'язана з тим, що при  всі операції в полі здійснюються за модулем мінімального полінома елемента всі операції в полі здійснюються за модулем мінімального полінома елемента  . .
Примітивний елемент  тут є утворюючим елементом мультиплікативної групи поля. слід базис розширений поле тут є утворюючим елементом мультиплікативної групи поля. слід базис розширений поле
Наприклад. Розглянемо поле 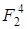 . Елементами цього поля є 16 векторів. . Елементами цього поля є 16 векторів.
Таблиця 1.
| (0000) |
(0001) |
(0010) |
(0011) |
(0100) |
(0101) |
(0110) |
(0111) |
| (1000) |
(1001) |
(1010) |
(1011) |
(1100) |
(1101) |
(1110) |
(1111) |
Використовуємо при обчисленнях поліном  (незвідний) (незвідний)
Додавання:
(0101)+(1101) = (1000).
Множення:
(0101)×(1101) =

Піднесення до степеня: 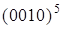
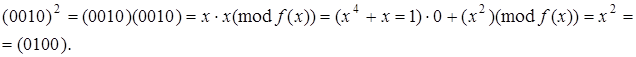 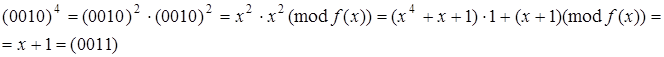 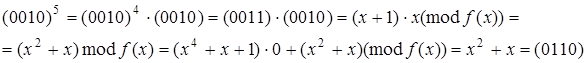
Таблиця 2 - Мультиплікативна інверсія
Мультиплікативною інверсією для  є є
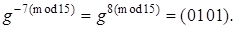
Дійсно  . .
Нормальний базис (НБ) над полем  визначається як множина сполучених елементів поля визначається як множина сполучених елементів поля  з підходящим вибором елемента з підходящим вибором елемента  . Розглянемо далі властивості НБ . Розглянемо далі властивості НБ  над полем над полем 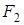 . На елемент . На елемент  тут накладається необхідна умова: тут накладається необхідна умова: . Водночас . Водночас  не обов'язково має бути примітивним. У будь-якому полі не обов'язково має бути примітивним. У будь-якому полі  існує елемент зі слідом 1, тому в будь-якому полі існує елемент зі слідом 1, тому в будь-якому полі  існує і НБ. Елементи НБ можна подати існує і НБ. Елементи НБ можна подати  -вимірними векторами. -вимірними векторами.

Зазначимо, що молодший розряд НБ звичайно записується ліворуч (на відміну від поліноміального, у якому молодший розряд прийнято записувати праворуч).
Кожен наступний елемент базису є циклічним зсувом вправо попереднього. Оскільки 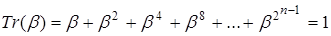 , елемент 1 поля , елемент 1 поля  визначається координатами визначається координатами  . Як бачимо, векторне подання елемента 1 поля . Як бачимо, векторне подання елемента 1 поля  в поліноміальному і нормальному базисах різні. в поліноміальному і нормальному базисах різні.
Для порівняння двійкове подання елементів у поліноміальному і нормальному базисах подано в таблиці 3.
Таблиця 2 - Двійкове подання елементів у поліноміальному і нормальному базисах
 |
 |
 |
 |
 |
 |
| 0 |
0000 |
0000 |
 |
1011 |
1110 |
| 1 |
0001 |
1111 |
 |
0101 |
0011 |
 |
0010 |
1001 |
 |
1010 |
0001 |
 |
0100 |
1100 |
 |
0111 |
1010 |
 |
1000 |
1000 |
 |
1110 |
1101 |
 |
0011 |
0110 |
 |
1111 |
0010 |
 |
0110 |
0101 |
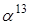 |
1101 |
1011 |
 |
1100 |
0100 |
 |
1001 |
0111 |
Довільний елемент поля в нормальному базисі подається як
 . .
Піднесення до квадрата елемента  в нормальному базисі дає в нормальному базисі дає
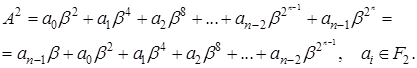
Таким чином, операція піднесення до квадрата (або витягу кореня квадратного) зводиться до циклічного зсуву вправо (або вліво) векторного подання елемента. Це одне з важливих технологічних переваг нормального базису перед поліноміальним. Іншою його перевагою є простота визначення сліду елемента. Дійсно:
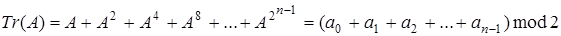 . .
Отже, слід елемента дорівнює 0 при парній вазі його векторного подання в НБ і 1 – при непарній вазі. Ця властивість радикально спрощує визначення сліду елемента у НБ.
Наприклад: елемент 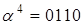 у нормальному базисі має парну вагу векторного подання. Слід цього елемента дорівнює 0 Дійсно у нормальному базисі має парну вагу векторного подання. Слід цього елемента дорівнює 0 Дійсно
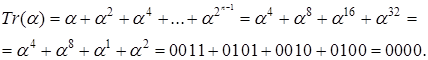
На наступній лекції ми розглядатимемо окремо т.з. оптимальний нормальний базис, який має значні переваги у швидкості та технологічності обчислень.
Під час обчислення точок з багаторазовими операціями додавання (віднімання) і подвоєння більш продуктивними є групові операції не в афінних координатах, а різного роду проективних координатах. Це дозволяє уникнути обчислення оберненого елемента в полі як самої трудомісткої операції й заощадити тимчасові обчислювальні ресурси.
У стандартних проективних координатах проективна точка 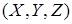 , ,  , відповідає афінній точці , відповідає афінній точці  Однорідне рівняння кривої після заміни змінних і множення на куб перемінної Однорідне рівняння кривої після заміни змінних і множення на куб перемінної  приймає вигляд приймає вигляд

(в афінних координатах рівняння кривої має вигляд
 ). ).
Точка на нескінченності  є вже одним з розв’язків даного рівняння. Зворотна точка тут, як і раніше, визначається інверсією знака є вже одним з розв’язків даного рівняння. Зворотна точка тут, як і раніше, визначається інверсією знака  координати координати
Подібно тому, як в афінних координатах, сумою точок 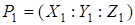 і і  при при  називається точка називається точка  , координати якої (позначення , координати якої (позначення  надалі опускається для скорочення запису) рівні: надалі опускається для скорочення запису) рівні:
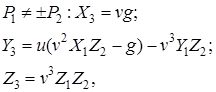
де 
Операцію підсумовування однакових точок  називають подвоєнням, а координати точки називають подвоєнням, а координати точки  дорівнюють: дорівнюють:

де 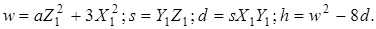
Час виконання операції додавання  і подвоєння і подвоєння 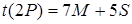 , де , де  позначає проективне подання точки. позначає проективне подання точки.
Наступний вид проективних координат - якобіанові координати.
До них можна перейти ізоморфним перетворенням координат, помноживши рівняння 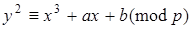 на на  , при цьому отримаємо: , при цьому отримаємо:
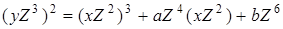 або або

де 
Сумою точок 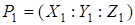 і і  при при  є точка є точка  , координати якої визначаються як: , координати якої визначаються як:
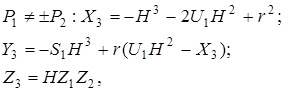
де 
При подвоєнні точки кривої отримаємо  : :

де  . .
У даному випадку час виконання складає  і і  , де , де  позначає якобіаново подання точки. позначає якобіаново подання точки.
Замість трьох якобіанових координат точки Чудновський запропонував використовувати п'ять:  Рівняння кривої описується формулою Рівняння кривої описується формулою  , а сума точок , а сума точок
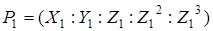 і і 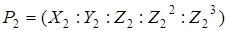
при  визначається як точка визначається як точка 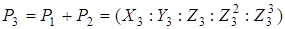 , координати Чудновського якої рівні: , координати Чудновського якої рівні:

Де

При подвоєнні точки кривої одержимо
 : :

де  . .
Час виконання складе  і і  , де , де  означає подання точки в координатах Чудновського. означає подання точки в координатах Чудновського.
Модифіковані якобіанові координати для рівняння

кривої містять чотири координати 
Сума точок  і і  при при  визначається як точка визначається як точка 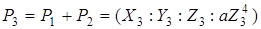 , модифіковані якобіанові координати якої дорівнюють: , модифіковані якобіанові координати якої дорівнюють:

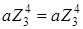 , ,
де 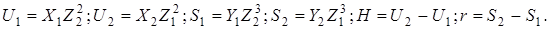
При подвоєнні точки кривої отримаємо


де 
Нарешті, можна зробити наступні оцінки. Час виконання дорівнює  і і  , де , де  означає подання точки в модифікованих якобіанових координатах. означає подання точки в модифікованих якобіанових координатах.
Формули, що визначають сумарне число  інверсій ( інверсій ( ), множень ), множень  і піднесень до квадрата і піднесень до квадрата  при додаванні і подвоєнні точок відповідно в афінних при додаванні і подвоєнні точок відповідно в афінних  , проективних , проективних  , якобіанових , якобіанових  координатах, координатах Чудновського координатах, координатах Чудновського 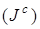 і модифікованих якобіанових координатах і модифікованих якобіанових координатах наведені в таблиці 1 (узагальнення). наведені в таблиці 1 (узагальнення).
За деякими оцінками, одна інверсія  , а піднесення до квадрата , а піднесення до квадрата  (при операціях у простому полі Галуа). Звідси стає зрозумілою доцільність переходу до проективних або до якобіанових координат, у яких операції інверсії відсутні. (при операціях у простому полі Галуа). Звідси стає зрозумілою доцільність переходу до проективних або до якобіанових координат, у яких операції інверсії відсутні.
Мінімальна обчислювальна складність додавання досягається за допомогою координат чудновського, а подвоєння – у модифікованих якобіанових координатах. Тому, звичайно, користуються змішаними координатами з метою оптимізації обчислень при багаторазовому додаванні точки.
Таблиця 3 - Число операцій множення  , піднесення до квадрата , піднесення до квадрата  й інверсій й інверсій  елементів простого поля при додаванні і подвоєнні точок у різних координатних системах елементів простого поля при додаванні і подвоєнні точок у різних координатних системах
Після обчислення точки  у змішаних координатах необхідно повернутися в афінні координати, для чого наприкінці обчислень потрібна одна інверсія. у змішаних координатах необхідно повернутися в афінні координати, для чого наприкінці обчислень потрібна одна інверсія.
|