Министерство образования и науки Российской Федерации
Федеральное агентство по образованию города Иркутска
Байкальский государственный университет экономики и права
Кафедра Информатики и Кибернетики
Распределение "хи-квадрат" и его применение
Самостоятельная работа
Автор работы:
Колмыкова Анна Андреевна
студентка 2 курса
группы ИС-09-1
Иркутск 2010
Введение
1. Распределение "хи-квадрат"
2. "Хи-квадрат" в задачах статистического анализа данных
Приложение
Заключение
Список используемой литературы
Как подходы, идеи и результаты теории вероятностей используются в нашей жизни?
Базой является вероятностная модель реального явления или процесса, т.е. математическая модель, в которой объективные соотношения выражены в терминах теории вероятностей. Вероятности используются, прежде всего, для описания неопределенностей, которые необходимо учитывать при принятии решений. Имеются в виду, как нежелательные возможности (риски), так и привлекательные ("счастливый случай"). Иногда случайность вносится в ситуацию сознательно, например, при жеребьевке, случайном отборе единиц для контроля, проведении лотерей или опросов потребителей.
Теория вероятностей позволяет по одним вероятностям рассчитать другие, интересующие исследователя.
Вероятностная модель явления или процесса является фундаментом математической статистики. Используются два параллельных ряда понятий – относящиеся к теории (вероятностной модели) и относящиеся к практике (выборке результатов наблюдений). Например, теоретической вероятности соответствует частота, найденная по выборке. Математическому ожиданию (теоретический ряд) соответствует выборочное среднее арифметическое (практический ряд). Как правило, выборочные характеристики являются оценками теоретических. При этом величины, относящиеся к теоретическому ряду, "находятся в головах исследователей", относятся к миру идей (по древнегреческому философу Платону), недоступны для непосредственного измерения. Исследователи располагают лишь выборочными данными, с помощью которых они стараются установить интересующие их свойства теоретической вероятностной модели.
Зачем же нужна вероятностная модель? Дело в том, что только с ее помощью можно перенести свойства, установленные по результатам анализа конкретной выборки, на другие выборки, а также на всю так называемую генеральную совокупность. Термин "генеральная совокупность" используется, когда речь идет о большой, но конечной совокупности изучаемых единиц. Например, о совокупности всех жителей России или совокупности всех потребителей растворимого кофе в Москве. Цель маркетинговых или социологических опросов состоит в том, чтобы утверждения, полученные по выборке из сотен или тысяч человек, перенести на генеральные совокупности в несколько миллионов человек. При контроле качества в роли генеральной совокупности выступает партия продукции.
Чтобы перенести выводы с выборки на более обширную совокупность, необходимы те или иные предположения о связи выборочных характеристик с характеристиками этой более обширной совокупности. Эти предположения основаны на соответствующей вероятностной модели.
Конечно, можно обрабатывать выборочные данные, не используя ту или иную вероятностную модель. Например, можно рассчитывать выборочное среднее арифметическое, подсчитывать частоту выполнения тех или иных условий и т.п. Однако результаты расчетов будут относиться только к конкретной выборке, перенос полученных с их помощью выводов на какую-либо иную совокупность некорректен. Иногда подобную деятельность называют "анализ данных". По сравнению с вероятностно-статистическими методами анализ данных имеет ограниченную познавательную ценность.
Итак, использование вероятностных моделей на основе оценивания и проверки гипотез с помощью выборочных характеристик – вот суть вероятностно-статистических методов принятия решений.
1.
Распределение "хи-квадрат"
С помощью нормального распределения определяются три распределения, которые в настоящее время часто используются при статистической обработке данных. Это распределения Пирсона ("хи – квадрат"), Стьюдента и Фишера.
Мы остановимся на распределении  ("хи – квадрат"). Впервые это распределение было исследовано астрономом Ф.Хельмертом в 1876 году. В связи с гауссовской теорией ошибок он исследовал суммы квадратов n независимых стандартно нормально распределенных случайных величин. Позднее Карл Пирсон (Karl Pearson) дал имя данной функции распределения "хи – квадрат". И сейчас распределение носит его имя. ("хи – квадрат"). Впервые это распределение было исследовано астрономом Ф.Хельмертом в 1876 году. В связи с гауссовской теорией ошибок он исследовал суммы квадратов n независимых стандартно нормально распределенных случайных величин. Позднее Карл Пирсон (Karl Pearson) дал имя данной функции распределения "хи – квадрат". И сейчас распределение носит его имя.
Благодаря тесной связи с нормальным распределением, χ2-распределение играет важную роль в теории вероятностей и математической статистике. χ2-распределение, и многие другие распределения, которые определяются посредством χ2-распределения (например - распределение Стьюдента), описывают выборочные распределения различных функций от нормально распределенных результатов наблюдений и используются для построения доверительных интервалов и статистических критериев.
Распределение Пирсона  (хи - квадрат) – распределение случайной величины (хи - квадрат) – распределение случайной величины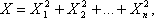 где X1, X2,…, Xn - нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение - единице. где X1, X2,…, Xn - нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение - единице.
Сумма квадратов

распределена по закону  ("хи – квадрат"). ("хи – квадрат").

Итак, распределение χ2 зависит от одного параметра n – числа степеней свободы.
Функция распределения χ2 имеет вид:
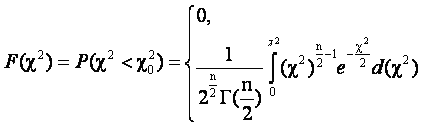
если χ2≥0. (2.7.)

Рисунок 1
Зависимость плотности вероятности φ (x) в распределении χ2 (хи – квадрат) при разном числе степеней свободы.
Моменты распределения "хи-квадрат":
M[χ2]=n
D[χ2]=2n
Распределение "хи-квадрат" используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных.
2. "Хи-квадрат" в задачах статистического анализа данных
Статистические методы анализа данных применяются практически во всех областях деятельности человека. Их используют всегда, когда необходимо получить и обосновать какие-либо суждения о группе (объектов или субъектов) с некоторой внутренней неоднородностью.
Современный этап развития статистических методов можно отсчитывать с 1900 г., когда англичанин К. Пирсон основал журнал "Biometrika". Первая треть ХХ в. прошла под знаком параметрической статистики. Изучались методы, основанные на анализе данных из параметрических семейств распределений, описываемых кривыми семейства Пирсона. Наиболее популярным было нормальное распределение. Для проверки гипотез использовались критерии Пирсона, Стьюдента, Фишера. Были предложены метод максимального правдоподобия, дисперсионный анализ, сформулированы основные идеи планирования эксперимента.
Распределение "хи-квадрат" является одним из наиболее широко используемых в статистике для проверки статистических гипотез. На основе распределения "хи-квадрат" построен один из наиболее мощных критериев согласия – критерий "хи-квадрата" Пирсона.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Критерий χ2 ("хи-квадрат") используется для проверки гипотезы различных распределений. В этом заключается его достоинство.
Расчетная формула критерия равна
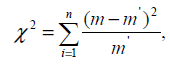
где m и m’ - соответственно эмпирические и теоретические частоты
рассматриваемого распределения;
n - число степеней свободы.
Для проверки нам необходимо сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.
При полном совпадении эмпирических частот с частотами, вычисленными или ожидаемыми S (Э – Т) = 0 и критерий χ2 тоже будет равен нулю. Если же S ( Э – Т) не равно нулю это укажет на несоответствие вычисленных частот эмпирическим частотам ряда. В таких случаях необходимо оценить значимость критерия χ2, который теоретически может изменяться от нуля до бесконечности. Это производится путем сравнения фактически полученной величины χ2ф с его критическим значением (χ2st).Нулевая гипотеза, т. е. предположение, что расхождение между эмпирическими и теоретическими или ожидаемыми частотами носит случайный характер, опровергается, если χ2ф больше или равно χ2st для принятого уровня значимости (a) и числа степеней свободы (n).
Распределение вероятных значений случайной величины χ2 непрерывно и ассиметрично. Оно зависит от числа степеней свободы (n) и приближается к нормальному распределению по мере увеличения числа наблюдений. Поэтому применение критерия χ2 к оценке дискретных распределений сопряжено с некоторыми погрешностями, которые сказываются на его величине, особенно на малочисленных выборках. Для получения более точных оценок выборка, распределяемая в вариационный ряд, должна иметь не менее 50 вариантов. Правильное применение критерия χ2 требует также, чтобы частоты вариантов в крайних классах не были бы меньше 5; если их меньше 5, то они объединяются с частотами соседних классов, чтобы в сумме составляли величину большую или равную 5. Соответственно объединению частот уменьшается и число классов (N). Число степеней свободы устанавливается по вторичному числу классов с учетом числа ограничений свободы вариации.
Так как точность определения критерия χ2 в значительной степени зависит от точности расчета теоретических частот (Т), для получения разности между эмпирическими и вычисленными частотами следует использовать неокругленные теоретические частоты.
В качестве примера возьмем исследование, опубликованное на сайте, который посвящен применению статистических методов в гуманитарных науках.
Критерий "Хи-квадрат" позволяет сравнивать распределения частот вне зависимости от того, распределены они нормально или нет.
Под частотой понимается количество появлений какого-либо события. Обычно, с частотой появления события имеют дело, когда переменные измерены в шкале наименований и другой их характеристики, кроме частоты подобрать невозможно или проблематично. Другими словами, когда переменная имеет качественные характеристики. Так же многие исследователи склонны переводить баллы теста в уровни (высокий, средний, низкий) и строить таблицы распределений баллов, чтобы узнать количество человек по этим уровням. Чтобы доказать, что в одном из уровней (в одной из категорий) количество человек действительно больше (меньше) так же используется коэффициент Хи-квадрат.
Разберем самый простой пример.
Среди младших подростков был проведён тест для выявления самооценки. Баллы теста были переведены в три уровня: высокий, средний, низкий. Частоты распределились следующим образом:
Высокий (В) 27 чел.
Средний (С) 12 чел.
Низкий (Н) 11 чел.
Очевидно, что детей с высокой самооценкой большинство, однако это нужно доказать статистически. Для этого используем критерий Хи-квадрат.
Наша задача проверить, отличаются ли полученные эмпирические данные от теоретически равновероятных. Для этого необходимо найти теоретические частоты. В нашем случае, теоретические частоты – это равновероятные частоты, которые находятся путём сложения всех частот и деления на количество категорий.
В нашем случае:
(В + С + Н)/3 = (27+12+11)/3 = 16,6
Формула для расчета критерия хи-квадрат:
χ2 = ∑(Э - Т)² / Т
Строим таблицу:
| Эмпирич. (Э) |
Теоретич. (Т) |
(Э - Т)² / Т |
| Высокий |
27 чел. |
16,6 |
6,41 |
| Средний |
12 чел. |
16,6 |
1,31 |
| Низкий |
11 чел. |
16,6 |
1,93 |
Находим сумму последнего столбца:
χ2= 9,64
Теперь нужно найти критическое значение критерия по таблице критических значений (Таблица 1 в приложении). Для этого нам понадобится число степеней свободы (n).
n = (R - 1) * (C - 1)
где R – количество строк в таблице, C – количество столбцов.
n = (R - 1) = 3-1 = 2
Для вероятности ошибки p≤0,05 и n = 2 критическое значение χ2 = 5,99.
| "Активный" |
"Старательный" |
"Дисциплинированный" |
| Мальчики |
10 |
5 |
6 |
| Девочки |
6 |
12 |
9 |
Для обработки полученных данных используем критерий хи-квадрат.
Для этого построим таблицу распределения эмпирических частот, т.е. тех частот, которые мы наблюдаем:
| "Активный" |
"Старательный" |
"Дисциплинированный" |
Итого: |
| Мальчики |
10 |
5 |
6 |
21 |
| Девочки |
6 |
12 |
9 |
27 |
| Итого: |
16 |
17 |
15 |
s=48 |
Теоретически, мы ожидаем, что частоты распределятся равновероятно, т.е. частота распределится пропорционально между мальчиками и девочками. Построим таблицу теоретических частот. Для этого умножим сумму по строке на сумму по столбцу и разделим получившееся число на общую сумму (s).
| "Активный" |
"Старательный" |
"Дисциплинированный" |
Итого: |
| Мальчики |
(21 * 16)/48 = 7 |
(21 * 17)/48 = 7.44 |
(21 * 15)/48 = 6.56 |
21 |
| Девочки |
(27 * 16)/48 = 9 |
(27 * 17)/48 = 9.56 |
(27 * 15)/48 = 8.44 |
27 |
| Итого: |
16 |
17 |
15 |
s=48 |
Итоговая таблица для вычислений будет выглядеть так:
| Категория 1 |
Категория 2 |
Эмпирич. (Э) |
Теоретич. (Т) |
(Э - Т)² / Т |
| Мальчики |
"Активный" |
10 |
7 |
1,28 |
| "Старательный" |
5 |
7,74 |
0,8 |
| "Дисциплинированный" |
6 |
6,56 |
0,47 |
| Девочки |
"Активный" |
6 |
9 |
1 |
| "Старательный" |
12 |
9,56 |
0,62 |
| "Дисциплинированный" |
9 |
8,44 |
0,04 |
| Сумма: 4,21 |
χ2 = ∑(Э - Т)² / Т
n = (R - 1), где R – количество строк в таблице.
В нашем случае хи-квадрат = 4,21; n = 2.
По таблице критических значений критерия находим: при n = 2 и уровне ошибки 0,05 критическое значение χ2 = 5,99.
Полученное значение меньше критического, а значит принимается нулевая гипотеза.
Вывод: учителя не придают значение полу ребенка при написании ему характеристики.
Критические точки распределения χ2
Таблица 1

Заключение
Студенты почти всех специальностей изучают в конце курса высшей математики раздел "теория вероятностей и математическая статистика", реально они знакомятся лишь с некоторыми основными понятиями и результатами, которых явно не достаточно для практической работы. С некоторыми математическими методами исследования студенты встречаются в специальных курсах (например, таких, как "Прогнозирование и технико-экономическое планирование", "Технико-экономический анализ", "Контроль качества продукции", "Маркетинг", "Контроллинг", "Математические методы прогнозирования", "Статистика" и др. – в случае студентов экономических специальностей), однако изложение в большинстве случаев носит весьма сокращенный и рецептурный характер. В результате знаний у специалистов по прикладной статистике недостаточно.
Поэтому большое значение имеет курс "Прикладная статистика" в технических вузах, а в экономических вузах – курса "Эконометрика", поскольку эконометрика – это, как известно, статистический анализ конкретных экономических данных.
Они необходимы специалистам для практической работы.
Я рассмотрела непрерывную вероятностную модель и постаралась на примерах показать ее используемость.
1. Орлов А.И. Прикладная статистика. М.: Издательство "Экзамен", 2004.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1999. – 479с.
3. Айвозян С.А. Теория вероятностей и прикладная статистика, т.1. М.: Юнити, 2001. – 656с.
4. Хамитов Г.П., Ведерникова Т.И. Вероятности и статистика. Иркутск: БГУЭП, 2006 – 272с.
5. Ежова Л.Н. Эконометрика. Иркутск: БГУЭП, 2002. – 314с.
6. Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. М. : Наука, 1975. – 111с.
7. Мостеллер Ф. Вероятность. М. : Мир, 1969. – 428с.
8. Яглом А.М. Вероятность и информация. М. : Наука, 1973. – 511с.
9. Чистяков В.П. Курс теории вероятностей. М.: Наука, 1982. – 256с.
10. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ, 2000. – 543с.
11. Математическая энциклопедия, т.1. М.: Советская энциклопедия, 1976. – 655с.
12. http://psystat.at.ua/ - Статистика в психологии и педагогике. Статья Критерий Хи-квадрат. Автор: Попов О.А.
|