КОНТРОЛЬНАЯ РАБОТА
на тему «Теория вероятности
»
по предмету «Математика»
Задание 1
Общее число возможных элементарных методов равно числу сочетаний из 10 по 5:
 . .
Подсчитываем число исходов, благоприятствующих нашему событию. Среди 3-х женщин две женщины могут быть выбраны 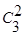 способами; при этом остальные 5–2=3 людей должны быть мужчинами. Взять же 3 мужчины из 7 можно способами; при этом остальные 5–2=3 людей должны быть мужчинами. Взять же 3 мужчины из 7 можно 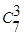 способами. Следовательно, число исходов благоприятствующих нашему событию: способами. Следовательно, число исходов благоприятствующих нашему событию:
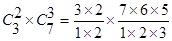 . .
Искомая вероятность равна:
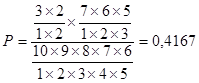 . .
Задание 2
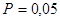 . .
Возможны следующие три случая:
А – среди трех студентов посетивших библиотеку первый заказал учебник по теории вероятностей, а два других не заказали;
В – второй студент заказал учебник по теории вероятностей, а первый и второй нет.
Вероятность каждого из этих событий по теореме умножения равны:
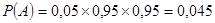 ; ;
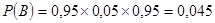 ; ;
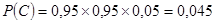 . .
Искомая вероятность по теореме сложения несовместных событий:
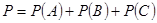 . .
Поэтому: 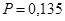 . .
Чтобы нити оказались одного цвета должны выполниться следующие события:
А – вынуть две нити красного цвета;
В – вынуть две нити белого цвета.
Вероятность каждого из этих событий по теореме умножения вероятностей будут:
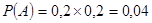 ; ;
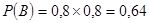 . .
Искомая вероятность по теореме сложения вероятностей: 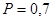 . .
Задание 3
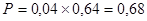 . .
I – 4б; 6кр; II – 5б; 10кр
Обозначим события А – выбранный шар белый. Можно сделать два предложения:
 – белый шар выбран из 1-го ящика – белый шар выбран из 1-го ящика
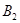 – белый шар выбран из 2-го ящика, так как ящик выбирают на удачу, то: – белый шар выбран из 2-го ящика, так как ящик выбирают на удачу, то:
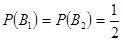 . .
Условная вероятность того, что шар будет белым и извлечен он из первого ящика будет:
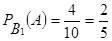 . .
Вероятность того, что белый шар будет извлечен из второго ящика:
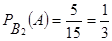 . .
Формула полной вероятности:
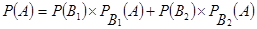 . .
Тогда вероятность того, что наугад взятый шар будет белым:
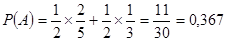 . .
Задание 4
Воспользуемся локальной теоремой Лапласа:
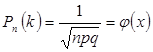 ; ;
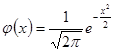 ; ;
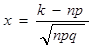 . .
В нашем случае n=600; k=25; P=0,05; q=0,95.
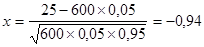 . .
Так как функция 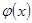 – четная, то по таблице находим: – четная, то по таблице находим:
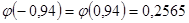 . .
Тогда 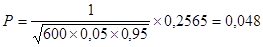 . .
Задание 5
| x |
20 |
25 |
30 |
35 |
40 |
| P |
0,2 |
0,3 |
0,2 |
0,1 |
0,2 |
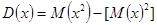 . .
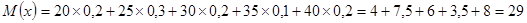 ; ;
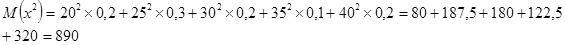 ; ;
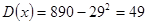 ; ;
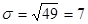 . .
Начальный момент первого порядка: 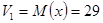 . .
Аналогично: 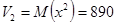 . .
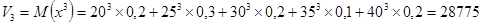 . .
Находим центральные моменты по формулам:
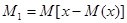 ; ;
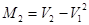 ; ;
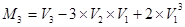 . .
Следовательно:
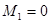 ; ;  ; ;  . .
Многоугольник распределения
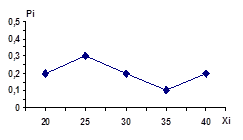
Задание 6
Распределение Х и распределение Y
| Xi
|
4 |
9 |
12 |
Yi
|
6 |
7 |
| Pi
|
0,36 |
0,24 |
0,4 |
Pi
|
0,65 |
0,35 |
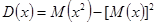 ; ;
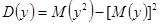 . .
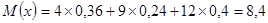 ; ;
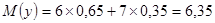 ; ;
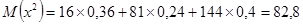 ; ;
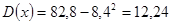 ; ;
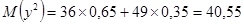 ; ;
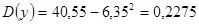 . .
Коэффициент коррекции находим по формуле:
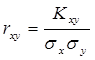 , ,
где: Kxy
– корелляционный момент связи случайных величин X и Y; 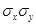 – среднеквадратические отклонения величин X и Y. – среднеквадратические отклонения величин X и Y.
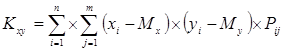 . .
Тогда:
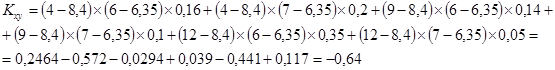 ; ;
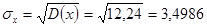 ; ;
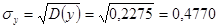 . .
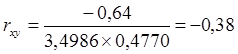 . .
Задание 7
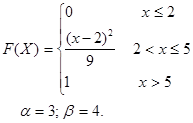 ; ; 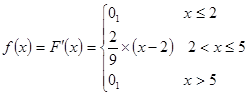 . .
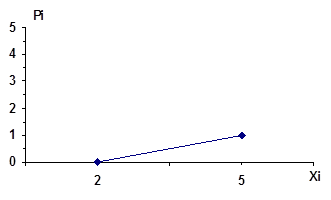
 ; ;
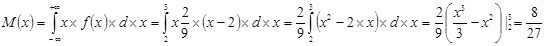 . .
Задание 8
Распределение Х и распределение Y
| Xi
|
1 |
3 |
5 |
Yi
|
12 |
13 |
15 |
| Pi
|
0,1 |
0,7 |
0,2 |
Pi
|
0,5 |
0,1 |
0,4 |
x1
=1; x2
=3; x3
=5; y1
=12; y2
=13; y3
=15; x1
+ y1
=13; x1
+ y2
=14; x1
+ y3
=16;
x2
+ y1
=15; x2
+ y2
=16; x2
+ y3
=18; x3
+ y1
=17; x3
+ y2
=18; x3
+ y3
=20;
Обозначим xi
+ yj
=7, тогда имеем следующие значения z:
z1
=13; z2
=14; z3
=15; z4
=16; z5
=17; z6
=18; z7
=20.
Соответствующие вероятности будут:
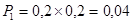 ; ;
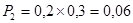 ; ;
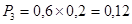 ; ;
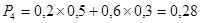 ; ;
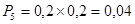 ; ;
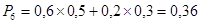 ; ;
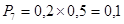 . .
Искомое распределение
| x+y |
13 |
14 |
15 |
16 |
17 |
18 |
20 |
| P |
0,04 |
0,06 |
0,12 |
0,28 |
0,04 |
0,36 |
0,10 |
Контроль:
0,04+0,06+0,12+0,28+0,04+0,36+0,1=1.
Задание 9
| Xi
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
| ni
|
1 |
2 |
3 |
4 |
5 |
10 |
6 |
5 |
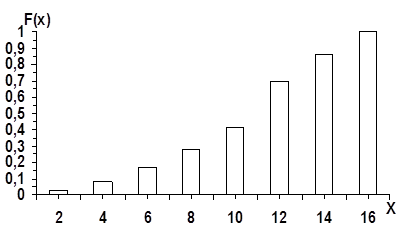
Находим значение эмпирической функции.
Вычисления выполняем в таблице.
Таблица вычислений
| Xi
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
Частота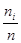 |
0,028 |
0,056 |
0,083 |
0,111 |
0,139 |
0,278 |
0,166 |
0,139 |
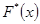 |
0,028 |
0,084 |
0,167 |
0,278 |
0,417 |
0,695 |
0,861 |
1,00 |
График эмпирической функции
Несмещенной оценкой генеральной средней является выборочная средняя:
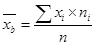 . .
Тогда:
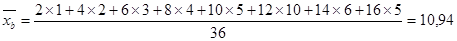 . .
Несмещенную оценку генеральной дисперсии найдем по формуле:
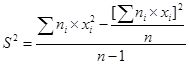
Последовательно находим:
 ; ;
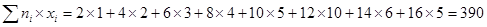 ; ;
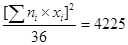 ; ;
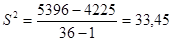 . .
Модой называют варианту, имеющую наибольшую частоту.
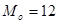 . .
Медиана:
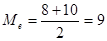 . .
Размах варьирования:
R=16–2=14.
Из соотношения 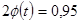 находим находим 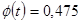 и t=1,96. и t=1,96.
Находим точность оценки по формуле:
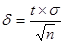 . .
Тогда:
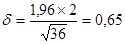 . .
Доверительный интервал таков: (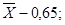  ). ).
|