«Использование обобщений при обучении математике в средней школе»
СОДЕРЖАНИЕ
Введение
Обобщение как метод научного познания в обучении математике
Методические особенности использования обобщений в изучении теоретического материала
Обобщение определений математических понятий и теорем
Подведение под понятие
Расширенные определения понятий
Расширенные теоремы-свойства понятий
Роль расширенных определений и теорем в процессе обучения
Возможные обобщения теоремы
Обобщения при решении задач на уроках математики
Обобщение в преподавании математики
Взаимосвязь обобщения и анализа
Обобщение как пример варьирования при поиске решения задач
Структурное представление технологии формирования обобщенного подхода к решению математических задач
Обобщение как эвристический прием решения нестандартных задач
Урок обобщения и систематизации знаний
Заключение
Литература
ВВЕДЕНИЕ
Известно, что математика оперирует определенными «идеальными» объектами. Однако все эти математические объекты отражают свойства материальных предметов и законы материального мира; их идеальный характер означает просто отвлечение от несущественных в момент рассмотрения свойств материальных вещей, благодаря чему исследуемые свойства выступают в наиболее общем и чистом виде. Поэтому все математические понятия и положения представляют собой знание наиболее глубоких и общих свойств реальной действительности.
В процессе познания законов природы математик пользуется особыми математическими средствами, научными методами исследования. В процессе обучения учащиеся также ставятся в положение первооткрывателей математических истин (самостоятельно или с помощью учителя) и поэтому научные методы математического исследования в то же время служат и методами учебной работы учащихся.
Основными методами математического исследования являются:
1) наблюдение и опыт;
2) сравнение;
3) анализ и синтез;
4) обобщение и специализация;
5) абстрагирование и конкретизация.
В данной курсовой работе будет изучен такой метод математического исследования, как обобщение, и выявлено его место и значение в преподавании, так как процесс изучения математики в школе неотделим от процесса ее преподавания.
ОБОБЩЕНИЕ КАК МЕТОД НАУЧНОГО ПОЗНАНИЯ В ОБУЧЕНИИ МАТЕМАТИКЕ.
Г.И. Саранцев по характеру учебно-познавательной деятельности и организации содержания материала выделяет следующие методы обучения математике:
· индуктивно-репродуктивный
(учитель создает такую ситуацию, в которой ученик воспроизводит понятие или теорему в процессе рассмотрения частных случаев. Например, посредством решения задач на выделение ситуаций, удовлетворяющих условию теоремы, или решение задачи (изучение теоремы) осуществляется по плану, предложенному учителем);
· индуктивно-эвристический
(метод предполагает самостоятельное открытие фактов в процессе рассмотрения частных случаев. Например, упражнения на умножение степеней с одинаковым основанием приводят к открытию определения произведения степеней с одинаковыми основаниями);
· индуктивно-исследовательский
(метод заключается в проведении исследований различных феноменов посредством изучения их конкретных проявлений. Например, изучая свойства четырехугольников в зависимости от наличия у них осей симметрии, приходим к таким видам четырехугольника, как прямоугольник, ромб, квадрат);
· дедуктивно-репродуктивный
(метод предполагает воспроизведение частных случаев в процессе решения задач, где используется общее положение. Например, теорема о сумме смежных углов воспроизводится посредством решения задач на нахождение одного из смежных углов, если задан другой);
· дедуктивно-эвристический
(метод заключается в открытии частностей какого-либо факта при рассмотрении общего случая. Примером проявления этого метода может служить решение любой конкретной задачи на применение какой-либо теоремы);
· дедуктивно-исследовательский
(Сутью этого метода обучения является организация исследований посредством дедуктивного развития учебного материала. Например, аксиоматический метод, метод моделирования, решение задач на применение теорем);
· обобщенно-репродуктивный
(цель достигается путем воспроизведения изученных фактов. Например, усвоение векторного метода предполагает овладение действиями перевода геометрического языка на векторный и обратно, сложения и вычитания векторов, представления вектора в виде суммы, разности векторов и т. п.);
· обобщенно-эвристический
(метод предполагает создание учителем такой ситуации, в которой ученик самостоятельно (или с небольшой помощью учителя) приходит к обобщению. Например, измеряя стороны и углы произвольных треугольников, ученики могут открыть следующую зависимость между углами и сторонами треугольника: против большей стороны треугольника лежит больший угол и наоборот);
· обобщенно-исследовательский
(метод предполагает наличие в учебном материале ситуаций, исследование которых приводит к обобщенному знанию. Например, рассматривая различные случаи расположения вписанных в окружность углов, можно прийти к известной теореме о том, что вписанный угол измеряется половиной дуги, на которую он опирается).
МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ ОБОБЩЕНИЙ В ИЗУЧЕНИИ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА
Обобщение определений математических понятий и теорем
Подведение под понятие
Важной особенностью математики как дедуктивной системы является то, что все понятия, за исключением основных, вводятся посредством определений. В определениях указываются некоторые специфические свойства понятий, называемые часто их признаками, по которым можно определить, принадлежит ли данный объект или отношение к объему этого понятия. Остальные свойства определяемых понятий устанавливаются в рассматриваемых о них теоремах. Одни из них дают достаточные условия существования данного понятия, а другие – необходимые условия существования данного понятия. Признаки понятий, выраженные посредством определений и теорем, обычно представляют собой различные простые высказывания, соединенные различными логическими операциями (связками). В каждом определении и в условии каждой теоремы признаки, дающие достаточные условия существования соответственного понятия, связаны связкой «и», т. е. образуют конъюнкцию. По этой причине, чтобы установить, принадлежит ли данный объект (или отношение) множеству объектов (или отношений), составляющих объем соответственного понятия, достаточно показать, что все его признаки имеют место в определении или условии одной из этих теорем. Деятельность, посредством которой доказывается, что определенный объект или отношение принадлежит соответственно множеству объектов или отношений, составляющих объем данного понятия, называется «подведением под понятие». В процессе решения задач почти всегда приходится устанавливать, что определенные объекты или отношения принадлежат объемам соответственных понятий, чтобы было возможно потом применить к ним теоремы, представляющие собой необходимые условия существования этих понятий. Именно этим способом, по известным свойствам данных объектов или отношений устанавливаются их другие, новые свойства.
Расширенные определения понятий
Если о некотором математическом понятии известно одно или больше определений и рассмотрены теоремы, дающие достаточные условия его существования, то отдельные конъюнкции признаков в этих определениях и теоремах образуют дизъюнкцию. Поэтому «подведение под понятие» можно алгоритмизировать. Для этой цели достаточно отдельные конъюнкции признаков в определениях и соответственных теоремах связать между собой в сложном высказывании посредством применения связки «или». Теперь достаточно проверить наличие каждой конъюнкции признаков, пока установится хотя бы одна. Такое сложное высказывание, представляющее собой дизъюнкцию признаков некоторого понятия, выраженных в отдельных определениях и теоремах, дающих достаточные условия существования этого понятия, называют расширенным определением существующего понятия.
Так как в процессе обучения сразу не рассматриваются все теоремы, дающие достаточные условия существования соответственных понятий, их расширенные определения усложняются постепенно.
Приведем пример расширенного определения параллелограмма, которое представляет собой определение типа «от рода к виду».
Четырехугольник 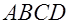 - параллелограмм
- параллелограмм  , если:
, если:
1) 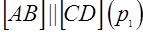 и
и 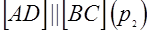 , или
, или
2) 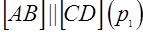 и
и 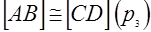 , или
, или
3) 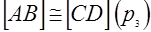 и
и 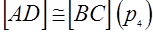 , или
, или
4) 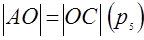 и
и 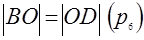 и
и 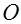 - точка пересечения диагоналей
- точка пересечения диагоналей 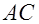 и
и 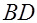 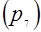 .
.
5)
Короче это расширенное определение можно записать так:
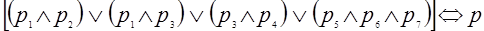 .
.
Это высказывание будет истинным в силу закона логики:
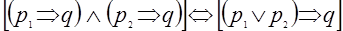 .
.
Если обозначить через 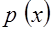 предикат, выражающий свойство четырехугольника «быть параллелограммом», то получим логическую функцию, заданную на множестве
предикат, выражающий свойство четырехугольника «быть параллелограммом», то получим логическую функцию, заданную на множестве 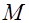 , составляющем объем родового понятия «четырехугольник». Каждый из признаков понятия «параллелограмм» можно также рассматривать как логическую функцию, заданную на том же множестве
, составляющем объем родового понятия «четырехугольник». Каждый из признаков понятия «параллелограмм» можно также рассматривать как логическую функцию, заданную на том же множестве 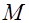 , так как каждым признаком задается свойство определенного подмножества множества
, так как каждым признаком задается свойство определенного подмножества множества 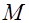 .
.
Если обозначить эти логические функции через 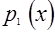 ,
, 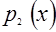 ,
, 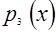 ,
, 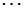 ,
, 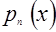 , то определение понятия «параллелограмм» можно записать в виде:
, то определение понятия «параллелограмм» можно записать в виде:
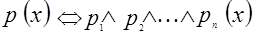 .
.
Тогда о произвольном, но фиксированном четырехугольнике 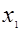 получаем высказывание: получаем высказывание:
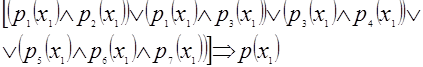 , ,
которое истинно, если истинна хотя бы одна из составляющих его дизъюнкций. В этом случае и можно утверждать, что произвольный, но фиксированный четырехугольник принадлежит множеству, представляющему объем понятия «параллелограмм».
Все, что было сказано выше об объектах, можно повторить и об отношениях, используя уже двухместные, трехместные и прочие предикаты.
Расширенные теоремы-свойства понятий
До сих пор мы рассмотрели применение теорем, дающих достаточные условия существования соответственных понятий. Рассмотрим теперь теоремы, которые дают необходимые условия существования данного понятия.
Обозначим через 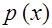 предикат «быть параллелограммом », через предикат «быть параллелограммом », через 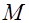 - множество, на котором определен этот предикат. Каждое необходимое свойство понятия «параллелограмм» можно рассматривать как логическую функцию, заданную на множестве - множество, на котором определен этот предикат. Каждое необходимое свойство понятия «параллелограмм» можно рассматривать как логическую функцию, заданную на множестве 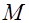 . .
Если обозначить эти логические функции через 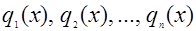 , то расширенную теорему о свойствах параллелограмма можно записать так: , то расширенную теорему о свойствах параллелограмма можно записать так:
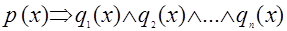 . .
Если произвольный, но фиксированный четырехугольник 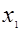 принадлежит объему понятия «параллелограмм», то в силу закона логики: принадлежит объему понятия «параллелограмм», то в силу закона логики:
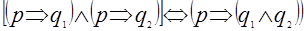
мы можем быть уверены, что 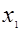 обладает свойствами обладает свойствами 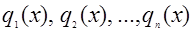 . .
Аналогичные расширенные определения и расширенные теоремы о свойствах можно поострить и для многих других понятий школьного курса математики (понятия конгруэнтности отрезков, углов, треугольников; параллельности прямых; понятия прямоугольник, ромб, квадрат, трапеция; параллельность прямой и плоскости, плоскостей; понятие корня квадратного уравнения; возрастающей и убывающей функции и т. д.).
Роль расширенных определений и теорем в процессе обучения
В процессе обучения математике целесообразно как можно чаще применять такие логические конструкции изучаемого материала, как расширенные определения и теоремы.
Чтобы лучше понять расширенных определений и расширенных теорем – свойств в обучении, отметим следующее. В традиционной методике после определения понятия рассматривались обычно весьма случайно отобранные теоремы, среди которых наряду с теоремами-признаками выступали и теоремы-свойства; при этом и те и другие теоремы не представляли собой логически организованной системы. Поэтому, применяя те или иные теоремы к решению задач, лишь немногие учащиеся оказывались способными самостоятельно использовать рассмотренное понятие или относящуюся к нему теорему при решении новых задач или изучении новых теорем.
Конструируя в процессе обучения все более широкие определения некоторого понятия или все более широкие совокупности теорем-свойств, мы тем самым устанавливаем органическую связь между свойствами понятия, отраженными в его определении, и другими свойствами, присущими только этому понятию. Доказав, что данный конкретный объект принадлежит к объему данного понятия, учащиеся актуализируют вои знания об изученном понятии, расширяют объем этих знаний, а значит, и возможности их приложения. Поэтому в процессе изучения понятий, аксиом и теорем рекомендуется сопоставлять вместе с учащимися постоянно дополняющиеся «списки», представляющие расширенные определения важнейших математических понятий или теорем-свойств.
Помимо логической организации изучаемого материала в сознании школьников, отмеченная выше методика работы с понятиями и теоремами делает сам процесс изучения математической теории более организованным и более естественным. Если учитель следует этой методике, его ученики будут ожидать, что после введения и определения нового понятия будут изучаться те его свойства, которые наряду с определение дадут возможности обнаружить это понятие в новой ситуации, а также использовать те свойства этой ситуации, которые имеют место. Если установлено наличие в ней данного понятия. Тем самым изучение теоремы и определения представляются учащимся в единой, взаимосвязанной системе, а не как случайно собранные вместе утверждения.
Возможные обобщения теоремы
Познакомимся с некоторыми способами обобщения, которые будем иллюстрировать утверждениями и задачами.
1.
Обобщение по размерности.
Известно следующее утверждение:
Если 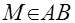 , то для любой точки , то для любой точки 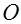 существуют такие числа существуют такие числа 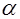 и и 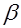 , что , что
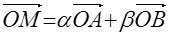 и
и 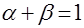 . .
Пользуясь обобщением по размерности, приходим к утверждению:
Если 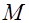 лежит в плоскости
лежит в плоскости 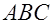 , то для любой точки
, то для любой точки 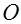 найдутся такие числа
найдутся такие числа 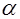 ,
, 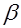 ,
, 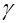 , что
, что
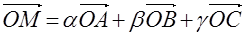 и
и 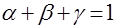 .
.
2.
Обобщение путем отбрасывания условий.
Данный способ особенно эффективен при решении задач. В частности, он используется тогда, когда не удается решить какую-либо задачу. С этой целью мы отбрасываем какое-либо условие или заменяем его на более слабое, а потом решаем новую задачу:
Доказать, что при
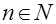 выполняется неравенство выполняется неравенство
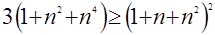 .
.
Здесь может быть отброшено условие 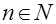 . Тогда, введя функцию
. Тогда, введя функцию 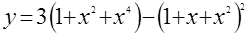 при
при 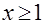 и используя производную, легко устанавливаем, что
и используя производную, легко устанавливаем, что 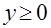 при
при 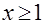 .
.
3.
Обобщение на основе рассмотрения частных случаев.
Этот метод особенно эффективен в том случае, если желательно угадать ответ. Рассмотрим известный пример:
Найти 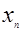 , если , если 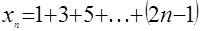 . .
Обращаемся к частным случаям:
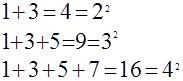
Это позволяет обобщить утверждение, высказав гипотезу, что 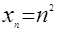 , а потом ее и доказать. , а потом ее и доказать.
4.
Обобщение на основе метода доказательства.
В ходе поиска решения задачи или доказательства теоремы мы нашли нужный метод. Анализируя метод, выясним, что он может быть использован в более общей ситуации. Это позволяет сформулировать и доказать обобщение утверждения.
Известна задача: Если в параллелограмме соединить середины смежных сторон, то полученный четырехугольник – параллелограмм.
Анализируя метод доказательства, можно получить известное обобщение.
5.
Обобщение путем изменения.
Анализируя объекты, которые входят в известное утверждение, заменяем их на другие и пытаемся сформулировать и доказать обобщения.
Обратимся к теореме Виета. В условии речь идет о трехчлене 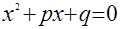 . Что можно менять? Это зависит от человека, который пытается обобщать, а точнее, какие объекты он увидит. Дело это творческое, и не существует единого рецепта. Обратимся к записи, где выделена часть объектов, которые могут быть изменены: . Что можно менять? Это зависит от человека, который пытается обобщать, а точнее, какие объекты он увидит. Дело это творческое, и не существует единого рецепта. Обратимся к записи, где выделена часть объектов, которые могут быть изменены:
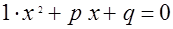
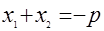
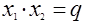
Без труда можно сформулировать возможные обобщения.
6.
Обобщение как усиление.
Этот метод поясняем на примере доказательства неравенства
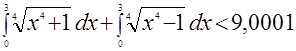 . .
Введем функцию 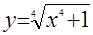 . Легко убедиться, что при . Легко убедиться, что при 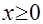 она возрастает и график является выпуклым вниз (рис. 1). она возрастает и график является выпуклым вниз (рис. 1).

рис. 1
Рассмотрим криволинейную трапецию 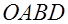 . Очевидно, что ее площадь . Очевидно, что ее площадь 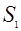 может быть вычислена по формуле может быть вычислена по формуле
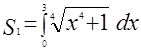 . .
Площадь криволинейного треугольника 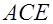 находится по формуле находится по формуле
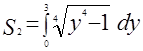 , или , или 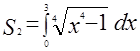 . .
Отсюда ясно, что в условии предлагается доказать, что
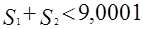 . .
Так как площадь квадрата 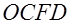 равна равна 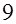 , то достаточно убедиться, что площадь криволинейного треугольника , то достаточно убедиться, что площадь криволинейного треугольника 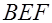 меньше меньше 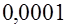 . Укажем координаты “нужных” точек: . Укажем координаты “нужных” точек:
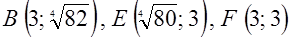 . .
Теперь рассмотрим точку 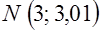 . Пользуясь выпуклостью вниз графика функции . Пользуясь выпуклостью вниз графика функции 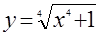 , легко убедиться, что площадь криволинейного треугольника , легко убедиться, что площадь криволинейного треугольника 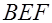 меньше площади треугольника меньше площади треугольника 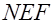 . Докажем неравенство . Докажем неравенство 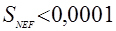 (это больше, чем нам нужно): (это больше, чем нам нужно):
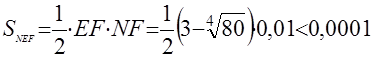 . .
Отсюда и получаем требуемое неравенство.
7.
Обобщение на основе соединения.
При данном способе обобщения новые утверждения получаются путем рассмотрения свойств объектов из разных тем (отметим, что этот метод отражен в названии наук – биофизика, биохимия, математическая биология и др.).
Известны следующие утверждения:
1. а) Если 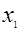 и и 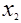 - корни трехчлена - корни трехчлена
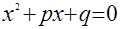 , то , то 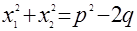 . .
б) Если 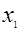 и и 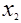 - любые числа, а - любые числа, а 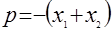 , , 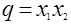 , то , то 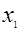 и и 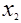 - корни уравнения - корни уравнения
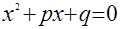 . .
2. Пусть 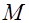 - точка касания вписанной в прямоугольный треугольник окружности с гипотенузой - точка касания вписанной в прямоугольный треугольник окружности с гипотенузой 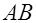 и и 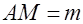 , , 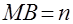 (рис. 2).
Доказать, что площадь треугольника равна
(рис. 2).
Доказать, что площадь треугольника равна 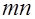 . .

рис. 2
Соединяя эти утверждения, можем сформулировать следующие задания:
Если 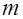 и и 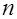 - отрезки, на которые точка касания окружности, вписанной в прямоугольный треугольник, разбивает гипотенузу, то: - отрезки, на которые точка касания окружности, вписанной в прямоугольный треугольник, разбивает гипотенузу, то:
а)
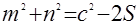 ; ;
б)
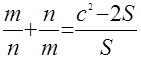 ; ;
в)
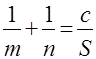 , ,
где
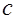 - гипотенуза, а - гипотенуза, а
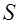 - площадь треугольника. - площадь треугольника.
ОБОБЩЕНИЯ ПРИ РЕШЕНИИ ЗАДАЧ НА УРОКАХ МАТЕМАТИКИ
Обобщение в преподавании математики
При обобщении мысленно выявляют какое-нибудь свойство, принадлежащее множеству объектов и объединяющее эти объекты воедино.
Так, например, изучение формулы n
-го члена арифметической прогрессии начинается с рассмотрения конкретных примеров на вычисление различных членов арифметической прогрессии по заданным первому ее члену и разности.
При проведении этих вычислений учащиеся используют равенства:
a2
= a1
+ d
,
a3
= a2
+ в =
(a1
+ d
) + в = a1
+ 2d
,
a4
= a3
+ в =
(a1
+ 2d
) + в = a1
+ 3d
ит. д.
Естественно, возникает полезное обобщение эти равенств в одной формуле an
=
a
1
+
d
(n
–
1), с помощью которой устанавливается более короткий способ для вычисления любого члена арифметической прогрессии.
В дальнейшем эта формула получает новое обобщение, когда устанавливается, что любая арифметическая прогрессия является линейной функцией натурального аргумента:
y
=
kx
+
b
, где x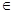 N
. N
.
Можно сказать, что обобщение выступает как переход от данного множества предметов к рассмотрению более «емкого» множества, содержащего данное.
Так, например, мы обобщаем, когда переходим от рассмотрения множества натуральных чисел к множеству дробных положительных чисел.
К обобщению могут привести: а) замена некоторой постоянной объекта переменной (треугольник 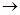 многоугольник); б) отказ от ограничения, наложенного на объект изучения многоугольник); б) отказ от ограничения, наложенного на объект изучения 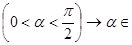 D
(D
– множество действительных чисел). D
(D
– множество действительных чисел).
Обобщение есть переход от рассмотрения единственного объекта к рассмотрению некоторого множества, содержащего этот объект в качестве своего элемента, или переход от менее емкого множества к более емкому, содержащему первоначальное.
1. Если случайно мы встречаем сумму
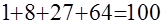 , ,
мы можем подметить, что ее можно записать в любопытной форме:
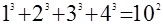 . .
Естественно возникает вопрос: часто ли сумма кубов последовательных чисел, т.е.
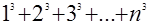 , ,
оказывается полным квадратом? Задавая этот вопрос, мы обобщаем.
Наше обобщение очень удачно: оно приводит нас от одного наблюденного факта к замечательному общему закону. Многие результаты в математике, физике и других естественных науках были найдены в результате удачного обобщения.
2. Обобщение часто может помочь решить задачу. Рассмотрим следующую стереометрическую задачу:
«Правильный октаэдр и прямая занимают в пространстве фиксированное положение. Найти плоскость, проходящую через данную прямую и делящую октаэдр на две равновеликие части». Задача эта может показаться сложной; однако достаточно небольшого знакомства с формой правильного октаэдра, чтобы прийти к следующему обобщению:
«Замкнутая поверхность, обладающая центром симметрии
, и прямая занимают в пространстве фиксированное положение. Найти плоскость, проходящую через данную прямую и делящую объем тела, ограниченного данной поверхностью, на две равновеликие части». Искомая плоскость, конечно, проходит через центр симметрии поверхности и определяется этой точкой и данной прямой. Так как октаэдр обладает центром симметрии, тем самым первоначальная задача оказывается решенной.
Конечно, нельзя не заметить, что вторая задача была более общей, чем первая, и, тем не менее, она оказалась проще. Нашим главным достижением при решении первой задачи было то, что мы придумали вторую задачу.
Придумав вторую задачу, мы выяснили роль центра симметрии; мы выделили
то свойство октаэдра, которое является существенным в данной задаче, именно – наличие у него центра симметрии.
Более общая задача может оказаться проще. Это звучит парадоксально; однако рассмотренный пример убеждает нас в истинности этого утверждения. Главное достижение при решении частной задачи состояло в том, что мы придумали общую задачу. После этого нам осталось совсем немного работы, чтобы довести задачу до конца.
Итак, в рассматриваем случае решение общей задачи явилось лишь общей частью решения частной задачи.
3. «Найти объем усеченной пирамиды с квадратным основанием, если сторона нижнего основания равна 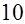 м
, сторона верхнего м
, сторона верхнего 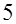 м
и высота пирамиды м
и высота пирамиды 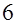 м
». Если числа м
». Если числа 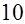 , , 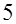 , , 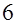 мы заменим буквами, например мы заменим буквами, например 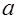 , , 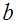 , ,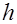 , мы тем самым обобщим задачу, более общую по сравнению с первоначальной, именно: , мы тем самым обобщим задачу, более общую по сравнению с первоначальной, именно:
«Найти объем усеченной пирамиды с квадратным основанием, если сторона нижнего основания равна 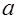 , сторона верхнего , сторона верхнего 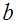 и высота пирамиды и высота пирамиды 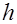 ». Подобное обобщение может оказаться очень полезным. Перейдя от задачи «в числах» к задаче «в буквах», мы приобретаем новые возможности; так, например, мы оказываемся в состоянии на данные величины как на переменные, что дает нам разнообразные возможности проверки результата. ». Подобное обобщение может оказаться очень полезным. Перейдя от задачи «в числах» к задаче «в буквах», мы приобретаем новые возможности; так, например, мы оказываемся в состоянии на данные величины как на переменные, что дает нам разнообразные возможности проверки результата.
Взаимосвязь обобщения и анализа
Рассмотрим пример зависимости обобщения и анализа. Результаты действий (как практических, так и мыслительных) над какими-либо объектами обычно определяются взаимным соотношением этих объектов и их свойств. Действия как бы служат средством для проведения анализа, с помощью которого эти соотношения устанавливаются.
На одном из экспериментальных занятий учащимся была предложена следующая задача: «Доказать, что треугольники ABO
и DCO
, заключенные между диагоналями трапеции, равновелики» (рис. 3). Наряду с этой основной задачей учащимся была предложена и другая, вспомогательная задача, менее трудная для решения и вместе с тем такая, что ее решение и решение основной задачи было основано на одном и том же принципе. В этой вспомогательной задаче требовалось доказать конгруэнтность диагоналей прямоугольника ABCD
(рис. 4).

рис. 3 рис. 4
Убедиться в конгруэнтности диагоналей прямоугольника учащимся легко, так как по существу эта задача представляет собой известную учащимся теорему, восстановить ход доказательства которой нетрудно. После этого и основная задача была быстро решена учащимися, которые сумели осуществить мысленный «перенос» хода решения вспомогательной задачи на решение основной. Общим ключом к решению этой и другой задачи оказалось использование в ходе доказательства общего основания AD
треугольников ABD
и ACD
, которое в первом случае выступало как общее основание равновеликих, а во втором – конгруэнтных треугольников ABD
и ACD
. Для отыскания решения основной задачи достаточно было установить равновеликость фигур ABD
и ACD
(связанных с треугольниками ABO
и OCD
). Достаточно было выделить это звено решения двух данных задач в качестве существенно общего свойства, т. е. совершить обобщение.
Таким образом, возможность обобщения и использования его результата – переноса – в процессе решения этих задач зависели прежде всего от мысленного включения обеих задач в единый процесс аналитико-синтетической деятельности. Успешное проведение обобщения (и переноса) было обусловлено тем, что на отдельных этапах анализа учащимися совершалось соотнесение условий основной задачи и задачи-подсказки. Результат процесса (перенос, использование задачи-подсказки) зависел, таким образом, от работы, проведенной учащимися в процессе анализа условия основной задачи. Это оказалось возможным потому, что объект изучения (основная задача) был включен в систему связей и отношений с другим известным объектом (вспомогательная задача).
Аналогичную ситуацию мы можем неоднократно наблюдать в процессе обучения математике в школе. Вернувшись к примеру с прогрессиями, нетрудно обнаружить ту же схему умственной деятельности школьника при правильно поставленной методике изучения этого вопроса. В самом деле, анализируя каждую из данных последовательностей отдельно (а затем совместно), школьник выявляет существенные свойства, общие для некоторых их этих последовательностей, свойства, позволяющие выделить их в особый класс – арифметических прогрессий и провести естественно вытекающее отсюда обобщение – сформулировать определение прогрессии.
Таким образом, обобщение с анализом являются мощным средством для выявления существенных для решения данной задачи (вопроса) свойств.
ОБОБЩЕНИЕ КАК ПРИМЕР ВАРЬИРОВАНИЯ ПРИ ПОИСКЕ РЕШЕНИЯ ЗАДАЧ
В современных условиях модернизации образования осуществляется обновление содержания и совершенствование механизмов обучения и контроля за качеством, что предполагает: принятие государственных стандартов общего образования; его разгрузку, ориентацию на потребности личности и современную жизнь страны; экспериментальную обработку нового содержания общего образования и т.д.
Говоря о творчестве в любой области деятельности человека, мы всегда обращаемся к понятию гибкости мышления, от активности формирования которого зависит темп обучения.
К числу способностей человека, дающих ему возможность успешно осуществлять творческую деятельность, Ю.М.Колягин относит:
- способность к быстрому сосредоточению и переключению внимания с сохранением его устойчивости и интенсивности на любых избранных объектах (в частности, на объекте изучения или исследования);
- способность оценивать ситуацию сразу с различных точек зрения, способность видеть больше того, что есть и что очевидно;
- способность из многообразия свойств изучаемого объекта выделить наиболее важные и существенные и в том случае, когда эти свойства существуют в скрытом виде;
- способность к открытию различных связей между объектами идеями, умение использовать логические связи для проверки достоверности сделанного вывода.
Вышеназванные способности у человека не появляются автоматически сами по себе. Одним из путей их формирования является обеспечение динамики внимания, которая осуществляется вариативностью упражнений. Это позволяет преподавателю управлять процессом внимания и ведет к формированию гибкости мышления обучаемых.
Из всех видов варьирования на занятиях по методическим дисциплинам наиболее видное место занимает варьирование содержания обучения математике, связанное с решением вопросов уровневой и профильной дифференциации обучения, что объясняется наибольшей разработанностью данного вопроса исследователями.
Нас будет интересовать варьирование условий задачи как один из способов её решения. Пути поиска решения задачи отражает Д.Пойа в своих работах, не называя термина «варьирование». Но именно этот термин обобщает его рекомендации в области поисков решения задачи.
В самом деле, поиски решения задачи начинаются с анализа условий (Что дано? Что неизвестно? В чём состоит условие?). Казалось бы, это – пустая формальность, и чтобы уяснить суть условия, достаточно внимательно прочитать задачу, может быть, не один раз. Между тем, это не так. Действительно, могут встречаться такие ситуации, когда условие задачи представлено в неявной форме, и тогда её данные могут быть записаны не полностью. Итог – «задача не решается».
Например, в геометрической задаче среди числовых данных встречается условие, когда выполняется движение фигуры. Это означает, что каждый отрезок данной фигуры перешёл в равный ему отрезок. Если представленную здесь часть условия «не заменить», то кажется, что не хватает данных для решения.
В подобных случаях рекомендуется исключить в формулировке задачи условие о движении, ученикам задать вопросы: что изменилось в задаче? Для чего было дано автором это условие?
Иногда задачу требуется иллюстрировать чертежом (особенно, если она геометрическая). При решении текстовых алгебраических задач необходимо осуществить своеобразный перевод на чисто математический язык уравнений (иногда неравенств).
Всё названное – представление условия задачи и его запись в разных вариантах. Примеры варьирования условий задачи можно продолжить.
Иногда условие задачи или теоремы таково, что её можно разбить на несколько задач. Например:
«Доказать, что если при пересечении двух прямых третей либо равны внутренние накрест лежащие углы, либо равны соответственные углы, либо сумма внутренних односторонних углов равна 180, то прямые параллельны» (известная теорема).
Эта задача фактически состоит из трёх задач, условие каждой из которых начинается после очередного слова «либо»; а заключение – одно. Конечно, такую задачу целесообразно разбить на три разные, а затем показать, как может быть осуществлено обобщение результатов задачи.
Полезно тут же сформулировать задачу, обратную данной. Это тоже будут три разные задачи, условия которых одинаковы (две параллельные прямые пересечены третьей). А заключения различные.
Так путём варьирования формулировки задачи можно показать учащимся, как возможности обобщения задач, так и возможности разбития их на несколько.
Иногда частные случаи позволяют выявить следствия из задачи или теоремы. Например, следствие теоремы. «В равнобедренном треугольнике углы при основании равны» является предложение: «В равностороннем треугольнике все углы равны».
Наконец, условия задачи проанализированы, заключение ясно, всё чётко переформулировано так, как удобно ученику в данный момент, и можно переходить к поиску решения задачи.
Что рекомендует Д.Пойа? Первое: «Известна ли вам какая-нибудь родственная задача?» Если известна, то решение предлагаемой задачи становиться «решением по образцу», и его поиск совершенно не нужен.
Вторая рекомендация Д.Пойа: «Встречалась ли вам какая-нибудь задача с тем же неизвестным?» Этот вопрос далеко не всегда приведёт к правильному ответу на него.
Допустим, что нам требуется найти высоту в треугольнике. Какой метод использовать? Вспомнить о признаках равенства треугольников? О признаках подобия? О вычислении площадей треугольников? Или использовать факт о диаметре, перпендикулярном к хорде, выполнив какие-нибудь дополнительные построения?
Чтобы прояснить наши дальнейшие действия, нужно связать условие с заключением. Как? В текстовых задачах требуется обычно составить уравнение, а может быть, неравенство или систему неравенств для того, чтобы обеспечить такую связь. В геометрии полезно начать с обращения к определениям понятий, содержащихся в условии и заключении задачи. Вопрос: «не можем ли мы указать родственную задачу?» заставляет нас обратиться к аналогам, но иногда это приводит к ошибочному пути, так как сравнение в каждом из различных случаев производиться по различным основаниям, что учащимся не всегда видно.
Например, ученику кажутся аналогичными по способу решения следующие задачи.
1. Дан угол и внутри него две точки. Построить четырёхугольник минимального периметра, у которого две смежные вершины лежат в данных точках, а две другие – на сторонах данного угла.
2. Дана прямая х и две точки А и В по разные стороны от неё. Поместить на прямой х отрезок МN = а, так, чтобы длина ломаной АМNВ была наименьшей.
Основания для такого утверждения дают следующие общие факты из содержания задачи:
- требуется построить ломаную наименьшей длины;
- даны прямые и точки, взаимное расположение которых известно;
- заметно некоторое внешнее сходство чертежей.
Между тем, первая задача решается методом симметрии, вторая – методом параллельного переноса.
Прекрасным примером варьирования является обобщение
. При различных способах обобщения изменяется эффективность выбранной преподавателем методики обучения. Все знания, умения и навыки, формируемые у учащихся в обучении математике можно разделить на следующие:
- частные (они распространяются на один математический объект или бесконечно много таких объектов, например, знание таблицы Пифагора);
- обобщенные.
Очевидно, что между частными и обобщенными знаниями, умениями и навыками нет конкретной границы, они часто проявляются в единстве. Обобщить – это значит зафиксировать общее, что имеется в конкретной теме урока, т.е. в каждом объекте рассматриваемой совокупности. Обобщение в обучении математике – это мысленное выделение общих и существенных признаков математических объектов (или способов действий с ними) и объединение их на этой основе в пределах заданной области (темы, раздела, всего учебного предмета).
Вариативность обучения математике на наш взгляд не осуществима без обобщения.
В свою очередь, понимание и овладение учащимися в полной мере основными обобщениями в математике может произойти только посредством методов вариативного обучения.
Большое внимание обобщению уделяет Г.И.Саранцев, предлагая вниманию учащихся различные приёмы использования обобщения и конкретизации на примерах решения задач.
Структурное представление технологии формирования обобщенного подхода к решению математических задач
.
| Этапы |
Задачи |
Средства |
Результаты |
Диагностирование |
| 1 |
Выявление исходного уровня сформированности обобщенного подхода к решению задач по математике |
Разработать системы задач и заданий, ориентированных на формирование у учащихся обобщенного подхода к решению задач по математике. Развитие мыслительных операций классификаций, сравнения, систематизации, обобщения |
Технологические (учебные) карты, раскрывающие структуру деятельности учащихся по поиску решения задач. |
Умение отыскивать ход мыслительных операций при выборе способа решения математических задач. |
Математические диктанты, устные и письменные ответы, тестирование. |
| 2 |
Формирование методологических умений (общеучебных) |
Разработать модель управления формированием у учащихся обобщенного подхода к решению задач по математике |
Комплекс учебно-исследовательских заданий, структурно-логические схемы, диагностические материалы и критерии для определения уровня сформированности обобщенного подхода к решению задач по математике. |
Выделить главное, не оставляя без внимания второстепенное, владеть общим подходом к решению учебных задач. |
Диагностические работы, уроки-семинары по конструированию поиска решения задач. |
| 3 |
Решение задач на производственном уровне |
Использовать модель управления формированием у учащихся обобщенного подхода к решению задач по математике на продвинутом уровне |
Система задач для развития умений и навыков решать задачи на продвинутом уровне |
Использовать альтернативные способы решения задач, адаптировать теоретические знания к конкретным практическим ситуациям |
Педагогический эксперимент по апробации эффективности исследуемых технологий формирования у учащихся обобщенного подхода к решению задач по математике. |
| 4 |
Проведение практикумов по решению задач и эксперименту |
Раскрытие значимости технологии формирования обобщенного подхода к решению задач по математике |
Структурно-логические схемы, учебные карты, методические рекомендации |
Умения: осуществлять анализ при решении задач, пользоваться логическими операциями: синтез, сравнение, обобщение, определять последовательность действий в каждом конкретном случае |
Письменные диагностические работы. Научно-практическая конференция учащихся по теме исследования. |
ОБОБЩЕНИЕ КАК ЭВРИСТИЧЕСКИЙ ПРИЕМ РЕШЕНИЯ НЕСТАНДАРТНЫХ ЗАДАЧ
Решение многих некоторых задач предполагает использование эвристических приемов группы парадигмы
. Под парадигмой
понимается система приемов формоизменения текста условия задачи, с помощью которых учащийся по существу заменяет текст условия задачи в определенном смысле эквивалентным ему, но позволяющим в то же время быстрее обнаружить решение. Такая замена может осуществляться по преимуществу тремя путями.
1. Посредством соблюдения правил построения составных знаков математического языка из более простых выражений (синтаксическая парадигма).
К данному типу относятся следующие приемы: выражение одной переменной через другую, введение вспомогательной неизвестной, идентификация того или иного геометрического объекта в различных конфигурациях, реконструкция целого по частям, разбиение целого на части, инверсия – расположение рассматриваемых объектов в особом порядке, облегчающем решение.
2. Через переформулирование условия задачи на основе учета связей между знаками исходного языка описания заданной ситуации и их значениями (семантическая парадигма
). Сущность приемов, относящихся к данному типу, состоит в переходе от исходной к равносильной задаче путем перевода текста исходной задачи на другой язык, например, с естественного на символический при решении текстовых задач, или нахождение новой интерпретации заданных условий в рамках того же языка.
3. На основе использования логических законов контрапозиции и исключенного третьего (логическая парадигма
). Здесь в основном используется метод доказательства от противного, а также приведение контрпримера или подтверждающего примера.
Можно выделить вторую группу эвристических приемов, используемых при решении нестандартных задач, - группу эксперимента
. Если в предыдущем случае поиск решения задачи осуществлялся в основном за счет внешней модификации ее условия, без изменения самой задачной ситуации, то эвристические приемы второй группы предполагают активное вмешательство реципиента в ситуацию, описанную в задаче, которое осуществляется посредством анализа и экспериментального исследования взаимоотношений между данными и искомыми этой задачи. В данную группу входят следующие эвристические приемы: рассмотрение частных случаев (неполная индукция), использование предельного перехода, метод математической индукции, групповой анализ, различные дополнительные построения в геометрических задачах, метод малых изменений, использование соображений симметрии, применение свойств монотонности или непрерывности функций и другие.
Зачастую при решении нестандартной задачи используется не один эвристический прием, а сразу несколько, причем, может быть, из разных групп. Часто при решении задач наряду используются эвристические приемы группы парадигмы – метод от противного и идентификация геометрических объектов в рамках различных конфигураций. Каждый из затронутых выше эвристических приемов позволяет реализовать определенный набор мыслительных операций (анализ, синтез, обобщение, аналогию и т.п.). Для полноценного умственного развития учащихся при обучении математике целесообразно предусмотреть использование максимального количества различных эвристик.
Урок обобщения и систематизации знаний
Уроки обобщения и систематизации знаний проводятся по окончанию изучения темы или раздела учебного материала. Основное их назначение заключается в усвоении связей и отношений между понятиями, теоремами, в формировании целостного представления у учащихся об изученном материале. Наиболее сложным в подготовке такого урока является организация повторения, выбор средств систематизации и обобщения знаний и умений школьников. Следует иметь в виду, что логика обобщающего повторения содержательнее логики первоначального изучения учебного материала. Она предполагает выделение связей между основным и второстепенным, между блоками главного, а также во второстепенном материале. Среди средств систематизации и обобщения знаний и умений школьников особое место занимают упражнения, выполнение которых основано на актуализации всего комплекса знаний и умений, подлежащих систематизации, упражнения, ориентированные на углубление и расширение знаний, на применение обобщений в различных конкретных ситуациях. К упражнениям такого вида относят упражнения на составление таблиц, схем, на классификацию понятий, на выявление отношений между понятиями, на составление «родословных» понятий и теорем.
Следует иметь в виду, что обобщающие уроки могут заключать не только пройденную тему, но и изучение исходного материала из разных разделов.
В уроке обобщения и систематизации знаний выделяют следующие структурные элементы:
1) сообщение темы, цели, задачи урока и мотивации учебной деятельности школьников;
2) воспроизведение и коррекция опорных знаний;
3) повторение и анализ основных фактов, событий, явлений;
4) повторение, обобщение и систематизация понятий, усвоение соответствующей системы знаний, ведущих идей и основных теорий.
Рассмотрим конкретный пример урока обобщения и систематизации знаний.
Урок на тему «Иррациональные уравнения» (10 класс)
Цель: обобщить и систематизировать способы решения иррациональных уравнений и умения применять их в различных ситуациях.
Основными методами решения иррациональных уравнений являются:
1) метод возведения обеих частей уравнения в одну и ту же степень, т. е. замена уравнения 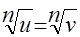 уравнением уравнением 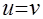 ; ;
2) метод введения новой переменной.
Однако зачастую иррациональные уравнения решаются с помощью рассуждений, основанных на анализе структуры уравнения, путем установления множества допустимых значений неизвестного, извлечения корня 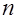 -ной степени из степени с показателем -ной степени из степени с показателем 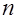 , на основе теорем равносильности. Отметим и то, что иррациональные уравнения могут содержать один, два и больше корней, причем они могут быть одной степени или разных степеней. Проиллюстрируем сказанное конкретными примерами. , на основе теорем равносильности. Отметим и то, что иррациональные уравнения могут содержать один, два и больше корней, причем они могут быть одной степени или разных степеней. Проиллюстрируем сказанное конкретными примерами.
1. Решите уравнения:
а) 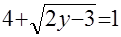 ; ;
б) 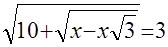 ; ;
в) 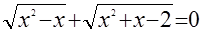 . .
Исследование структуры уравнения а) показывает, что оно не имеет корней, так как 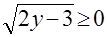 , и потому , и потому 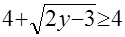 ; в случае б) имеем ; в случае б) имеем 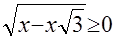 при допустимых значениях при допустимых значениях 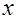 и и 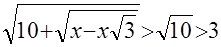 . Анализ структуры уравнения в) показывает, что его решением является каждое значение . Анализ структуры уравнения в) показывает, что его решением является каждое значение 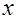 , для которого одновременно , для которого одновременно 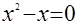 и и 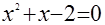 . Этому требованию удовлетворяет . Этому требованию удовлетворяет 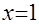 . .
2. Решите уравнения:
а) 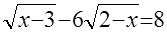 ; ;
б) 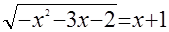 . .
Подкоренные выражения просты, поэтому целесообразно, прежде всего, выявить множество допустимых значений неизвестного. Легко установить, что область определения уравнения а) – пустое множество, а потому уравнение не имеет решений. В случае б) уравнение может иметь решение при 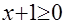 , т. е. при , т. е. при 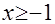 . Учитывая, что левая часть уравнения имеет смысл при . Учитывая, что левая часть уравнения имеет смысл при 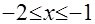 , получаем, что уравнение имеет единственный корень: , получаем, что уравнение имеет единственный корень: 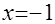 . .
3. Решите уравнения:
а) 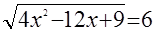 ; ;
б) 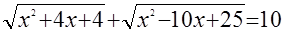 . .
Уравнения а) и б) можно записать соответственно в виде:
а) 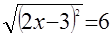 ; ;
б) 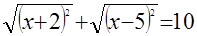 , ,
которые, в свою очередь, равносильны уравнениям:
а) 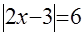 ; ;
б) 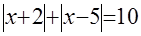 . .
Решим уравнение б), для чего воспользуемся методом интервалов:
1) при 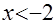 уравнение уравнение 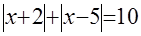 равносильно уравнению равносильно уравнению 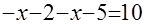 , корнем которого является , корнем которого является 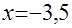 ; ;
2) если 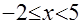 , то исходное уравнение равносильно уравнению , то исходное уравнение равносильно уравнению 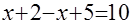 или или 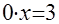 , которое не имеет решений; , которое не имеет решений;
3) при 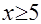 уравнение уравнение 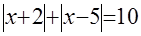 преобразуется в уравнение преобразуется в уравнение 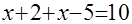 , или , или 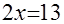 , откуда , откуда 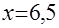 . .
Часто решение иррациональных уравнений основывается на возведении обеих частей уравнения в одну и ту же степень. Рассмотрим, например, решение уравнения 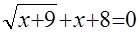 . Запишем данное уравнение в виде . Запишем данное уравнение в виде 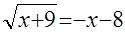 и возведем обе его части в квадрат. Получим и возведем обе его части в квадрат. Получим
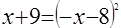 , ,
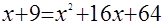 , , 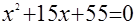 , ,
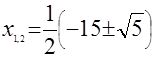 . .
Так как при возведении обеих частей уравнения в одну и ту же степень возможно появление посторонних корней, то обязательна проверка найденных корней. Число 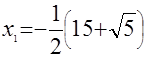 удовлетворяет исходному уравнению, а число удовлетворяет исходному уравнению, а число 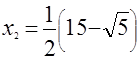 нет. нет.
Уравнение 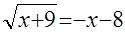 можно решить с применением теорем равносильности. Известно, что уравнение можно решить с применением теорем равносильности. Известно, что уравнение 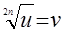 равносильно системе равносильно системе
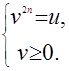
Заданное уравнение равносильно системе 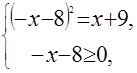
которая имеет единственное решение 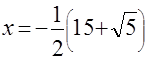 . .
К решению исходного уравнения можно было бы применить и метод введения новой переменной. Запишем данное уравнение в виде 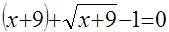 . Положив . Положив 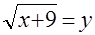 , получаем , получаем 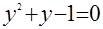 . Продолжение решения не вызывает трудностей. . Продолжение решения не вызывает трудностей.
Рассмотрим еще пример уравнения, содержащего квадратные, кубические и другие корни.
Решите уравнения:
а) 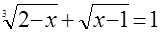 ; ;
б) 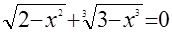 . .
Положив в уравнении а) 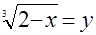 и и 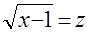 , приходим к системе уравнений , приходим к системе уравнений 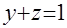 и и 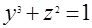 , откуда , откуда 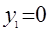 , , 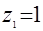 ; ; 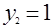 , , 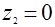 ; ; 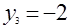 , , 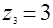 . .
Подставив в одно из равенств значения 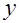 или или 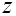 , получим , получим 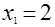 , , 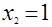 , , 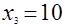 . .
Область допустимых значений уравнения б) такова: 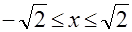 . Если . Если 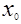 - корень уравнения, то - корень уравнения, то 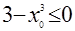 , или , или  . Но . Но 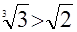 , следовательно, уравнение б) не имеет решений. , следовательно, уравнение б) не имеет решений.
Систематизация и обобщение указанных способов решения иррациональных уравнений и составляет содержание рассматриваемого урока. Осуществляется она в процессе выполнения следующих упражнений:
1.
Назовите, какие из данных уравнений иррациональные:
а) 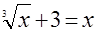 ; ;
б) 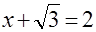 ; ;
в) 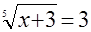 ; ;
г) 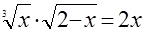 ; ;
д) 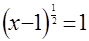 ; ;
е) 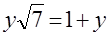 . .
Иррациональные уравнения, содержащие только квадратные корни.
2.
Решите каждое из уравнений:
а) 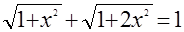 ; ;
б) 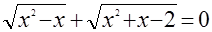 . .
3.
Решите уравнения:
а) 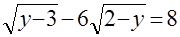 ; ;
б) 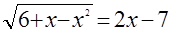 . .
4.
Решите уравнения:
а) 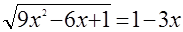 ; ;
б) 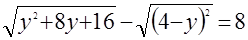 . .
5.
Дано уравнение 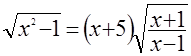 . Почему и где в нижеуказанных в связи с его решением рассуждениях «потерян» корень? . Почему и где в нижеуказанных в связи с его решением рассуждениях «потерян» корень?
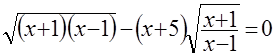 , ,
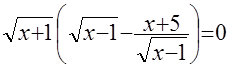 , ,
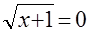 , , 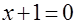 , , 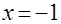 , ,
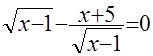 , , 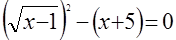 , ,
 , , 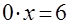 . Решений нет. . Решений нет.
Найдите «потерянный» корень.
6.
Дано уравнение 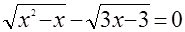 . Прокомментируйте следующие его решения: . Прокомментируйте следующие его решения:
а) 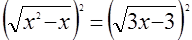 , , 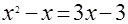 , , 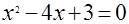 , , 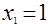 , , 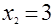 ; ;
б) 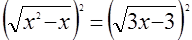 , ,  , , 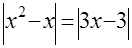 . .
а. 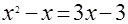 , , 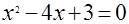 , , 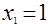 , , 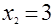 ; ;
б. 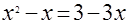 , , 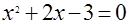 , , 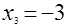 , , 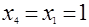 . .
7.
Решите уравнения:
а) 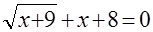 ; ;
б) 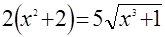 . .
8.
Решите уравнения:
а) 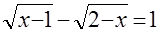 ; ;
б) 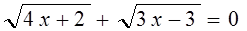 . .
Иррациональные уравнения, содержащие квадратные, кубические и другие корни.
9.
Решите уравнения:
а) 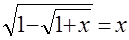 ; ;
б) 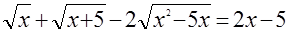 . .
Учитывая сложность темы «Иррациональные уравнения», для обобщающего урока целесообразно планировать сдвоенный урок. Формы выполнения упражнений могут быть различны: выполнение упражнений у доски, комментированное решение, самостоятельная работа и т. д.
ЗАКЛЮЧЕНИЕ
Следует отметить, что включение учащихся в деятельность по отысканию обобщений математических фактов играет большую роль в воспитании качеств творческой личности. При этом ученики учатся самостоятельно ставить и решать новые для них задачи, учатся продуктивному умственному труду. Кроме того, такая деятельность способствует лучшему усвоению знаний, обнаружению связей между ними, учит рассматривать определенные факты, закономерности с более общей точки зрения, с позиции общих закономерностей, что чрезвычайно важно при изучении математики.
ЛИТЕРАТУРА.
1. Саранцев Г. И. «Упражнения в обучении математике». – М.: Просвещение, 1995.
2. Саранцев Г. И. «Общая методика преподавания математики» - М.: Просвещение, 1999.
3. Оганесян В. А., Колягин Ю.М., Луканкин Г. Л., Саннинский В. Я. «Методика преподавания математики в средней школе». – М.: Педагогика, 1976.
4. Пойа Д. «Как решать задачу?».
5. Зильберберг Н. И. «Урок математики. Подготовка и проведение». – М.: Просвещение, 1996.
6. Епишева О. Б., Крупич В. И. «Учить школьников учиться математике».
7. Пичурин Л. Ф. «Воспитание учащихся при обучении математике».
|