ВВЕДЕНИЕ
В различных направлениях проводятся теоретические исследования в области экономической динамики. Все динамические макромодели, как аналитические, так и допускающие лишь количественные исследования, можно условно разделить на две группы. К первой относятся модели экономического роста, ко второй - модели экономического цикла или, в более широком смысле, экономических колебаний.
Изучением экономических циклов занимались такие выдающиеся экономисты как Самуэльсон Пол (труды по проблемам моделирования экономического цикла, экономико-математическим методам измерения полезности и др. Лауреат Нобелевской премии (1970)), Джон Хикс - английский экономист; труды в области моделирования экономического роста, теории спроса, цен. Лауреат Нобелевской премии (1972).
Целью данной работы является теоретическое и практическое изучение модели экономического цикла Самуэльсона-Хикса.
Актуальность моей темы обуславливается тем, что на данный момент мировая экономика переживает кризис.
Перед данной работой ставятся следующие задачи: определение понятия экономического цикла; рассмотрение линейных конечно-разностных уравнений второго порядка и их применение в экономике; изучение модели взаимодействия мультипликатора-акселератора; анализ модели экономического цикла Самуэльсона-Хикса и ее применение.
При работе над курсовой были использованы доступные для изучения материалы учебных пособий по экономике, математическому анализу, работы ведущих экономистов и математиков, справочные издания, научные и аналитические статьи, опубликованные в Интернет - изданиях.
ГЛАВА 1. АНАЛИЗ ЭКОНОМИЧЕСКОГО ЦИКЛА
1.1Понятие экономического цикла
Теория экономического цикла исследует причины, вызывающие изменение экономической активности общества. Она исследует, почему равенство совокупного предложения совокупному спросу достигается при разной степени использования производственных мощностей и трудовых ресурсов. Теория экономических циклов наряду с теорией экономического роста объясняет характер развития экономики во времени. Обобщающим показателем величины и направления изменения экономической активности служит уровень использования производственного потенциала страны. Статистические данные свидетельствуют, что изменение показателей, характеризующих результаты национальных хозяйств, изменяются не монотонно, а колебательно (циклически). На рис.1 показаны темпы прироста ВВП в четырех наиболее успешно развивавшихся во второй половине ХХ в. странах.
 [1] [1]
Рис. 1 Годовые темпы прироста ВВП США, Великобритании, ФРГ и Канады в 1951-1992 гг. (%%)
Направление и степень изменения показателя или совокупности показателей, характеризующих развитие народного хозяйства, определяют как экономическую конъюнктуру. Поэтому теорию экономических циклов называют также теорией конъюнктуры. Под экономическим циклом подразумевается период развития экономики между двумя одинаковыми состояниями конъюнктуры.
При более подробном анализе экономический цикл делят на четыре фазы.
1. Рецессия (кризис)
. В этой стадии производство сокращается, (темпы прироста становятся отрицательными), растет безработица и снижается совокупный спрос.
2. Депрессия
. Национальный доход продолжает снижаться, но темпы падения замедляются; поэтому кривая темпов прироста "поворачивается" вверх.
3. Оживление
Переход от падения производства к его увеличению; постепенное возвращение экономики к состоянию, соответствующему равновесному росту.
4. Экспансия
(пик/бум) Национальный доход растет, несмотря на полную занятость. Увеличивается спрос на инвестиции, безработица снижается ниже естественного уровня. Повышаются уровень цен, ставка заработной платы и ставка процента. Неизбежным следствием такого развития событий является переход от роста к спаду. .
Исходной фазой экономического цикла является кризис. Речь идет об общем периодическом кризисе перепроизводства. В этот момент наблюдается падение уровня и темпов экономического роста, сокращения масштабов выпуска изделий. Происходят массовые банкротства промышленных и торговых предприятий. Быстро растет безработица, сокращается заработная плата. В обществе нарушаются кредитные связи, расстраивается рынок ценных бумаг, падают курсы акций. Все предприниматели испытывают острую потребность в деньгах для уплаты быстро образовавшихся долгов и поэтому норма банковского процента значительно возрастает.
Затем наступает фаза депрессии. Тогда приостанавливается спад производства, а вместе с теми снижение цен. Постепенно уменьшаются запасы товаров. Из-за не значительного спроса увеличивается масса свободного денежного капитала и ставка банковского процента снижается до минимума. Уменьшаются цены на средства производства и удешевляется кредит, что способствует возобновлению расширенного воспроизводства на новой технической основе. В следующей фазе- оживлении -производство расширяется, размеры товарных запасов устанавливаются на уровне, необходимом для бесперебойного снабжения рынка. Начинается не большое повышение цен, сокращаются масштабы безработицы; возрастает спрос на денежный капитал и ставка процента увеличивается.
В период экспансии выпуск продукции превышает предкризисный уровень. Сокращается безработица. С расширением покупательского спроса возрастают цены на товары. Повышается прибыльность производства. Увеличивается спрос на кредитные средства и соответственно возрастает норма банковского процента. Графически экономический цикл может быть представлен в виде синусоиды (рис.2), где крайние точки (максимум и минимум) уровня экономической активности характеризуют экономический бум и кризис.
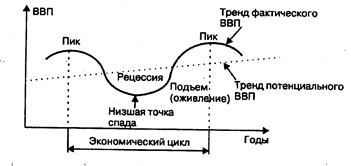 [2] [2]
Рис. 2. Стилизованные фазы экономического цикла
1.2 Модель взаимодействия мультипликатора-акселератора
Мультипликатор
— это коэффициент, выражающий соотношение между приростом дохода и вызывающим этот прирост увеличением объема инвестиций. Он показывает зависимость прироста национального дохода от прироста инвестиций. Мультипликатор увеличивается в том случае, когда потребители склонны использовать прирост их доходов для наращивания потребления. Напротив, он уменьшается, если усиливается склонность потребителей к накапливанию сбережений.
Рост частных инвестиций будет вызывать увеличение дохода, а сокращение инвестиций - его уменьшение, потому что инвестиции – это часть чистого национального продукта; если стоимость одной части возрастает, то мы должны предположить рост стоимости целого. Инвестируемые капиталовложения – как любые капиталовложения из независимых расходов государства или семьи – это капиталовложения повышенной мощности, выполняющие двойную полезную работу.[3]
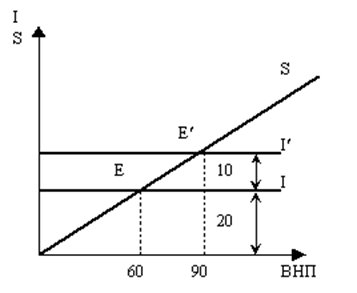
Рис. 3. Графическое изображение мультипликатора
Математически мультипликатор в наиболее общем виде выглядит:
k * ΔI= ΔY, (1)
где k – коэффициент мультипликации; ∆I - изменение инвестиций; ∆Y - изменение дохода.
Сущность принципа акселерации
заключается в следующем: возросший доход, полученный в результате возрастания первоначальных инвестиций, вызывает рост спроса на потребительские товары. Отрасли, производящие потребительские товары, начинают расширяться, а это, в свою очередь, приводит к росту спроса на товары производственного назначения, т.е. на средства производства. Причем изменения в спросе на потребительские товары вызывают гораздо более резкие изменения в спросе на товары производственного назначения. Это связано со специфическими особенностями воспроизводства основного капитала. Последний требует единовременных крупных затрат, которые возмещаются постепенно в течение длительного периода. Поэтому в случае необходимости расширения существующих или строительства новых предприятий затраты на создание нового основного капитала превосходят стоимость выпускаемой продукции. Отсюда следует, что принцип акселерации показывает, как в силу цепной зависимости между отраслями изменения в спросе на потребительские товары вызывают более сильные изменения в производстве средств производства, или капитальных товаров.
Математически принцип акселерации в наиболее общем форме выглядит:
I =  (Yt
-Yt-1
), (2) (Yt
-Yt-1
), (2)
где I — индуцированные инвестиции; Yt
— доход в период t; Yt-1
- доход в предшествующий ему период;  — коэффициент акселерации. — коэффициент акселерации.
Математически принцип мультипликатора – акселератора можно записать:Yt
= Ct
+ It
+ Gt
, (3)
где – Yt
- национальный доход; Ct
- объем потребления; It
- индуцированные чистые инвестиции в частном секторе; Gt
- автономные инвестиции (государственные расходы); t - индексы дискретного периода времени. Кроме того, считаются выполненными соотношения
Ct
= kYt
- 1
, (4)
It
=  (Ct
– Ct
- 1
), (5) (Ct
– Ct
- 1
), (5)
Gt
= const, (6)
где k - коэффициент мультипликации;  - коэффициент акселерации. - коэффициент акселерации.
Запаздывание, равное одному периоду, одновременно присутствует в процессах мультипликации и акселерации, которые описываются линейными зависимостями (4) - (5).
Эффект мультипликатора-акселератора показывает механизм самоподдерживающихся циклических колебаний экономической системы.
Рост инвестиций на определенную величину может увеличить национальный доход на многократно большую величину вследствие эффекта мультипликатора. Возросший доход, в свою очередь, вызовет в будущем опережающий рост инвестиций вследствие действия акселератора. Эти производные инвестиции, являясь элементом совокупного спроса, порождают очередной мультипликационный эффект, который снова увеличит доход, побуждая тем самым предпринимателей к новым инвестициям. Но не будем забывать, что как и эффект мультипликатора может действовать «в обратную сторону», так и эффект акселератора-мультипликатора может вызывать многократно большее снижение инвестиций, нежели изменение дохода (реального ВВП).
Таким образом, взаимодействие мультипликатора и акселератора порождает непрерывный и прогрессирующий рост выпуска продукции или дохода.
Если теоретически взаимодействие мультипликатора и акселератора допускает взрывоопасные колебания, то на практике взрывов не происходит, поскольку колебания дохода наталкиваются на определенные границы. Верхний предел роста национального дохода задается уровнем полной занятости. Ударившись об этот «потолок» рост реального дохода прекращается. Тогда производные инвестиции сокращаются до нуля, что в свою очередь, приводит к сокращению общего спроса и дохода. В своем падении национальный доход наталкивается на нижний предел, определяемый величиной амортизационных отчислений для простого восстановления основного капитала. Отрицательно чистые капиталовложения не могут превышать величины «изношенного» капитала. Достигнув этого уровня отрицательные инвестиции не меняются, а значит, сокращение дохода замедляется, а это, в свою очередь, ведет к сокращению отрицательных чистых капиталовложений, что обусловливает рост дохода, а за ним и индуцированных инвестиций. Таким образом, когда национальный доход достигает верхней или нижней границы, он меняет движение на противоположное, что исключает как взрыв, так и полное затухание цикла.
Рассмотрим механизм взаимодействия мультипликатора и акселератора на условном числовом примере. Пусть величина национального дохода в базовом и в двух предшествующих ему периодах равна 120. Базовый уровень автономных инвестиций - 48, предельная склонность к потреблению и акселератор постоянны и равны, соответственно, 0,6 и 0,7. Предположим, что в периоде 1 автономные инвестиции возросли с 48 до 60 и в дальнейшем сохранялись на этом уровне. Результаты данного инвестиционного всплеска отразим в Таблице 1.
Таблица 1 Пример действия эффекта мультипликатора-акселератора
| Период |
Сt
= MPC yt-1
|
It
a |
It
ин
= b(yt
– yt-1
) |
yt
= Ct
+ It
a+ It
ин
|
| 0 |
72 |
48 |
0 |
120 |
| 1 |
72 |
60 |
0 |
132 |
| 2 |
79,2 |
60 |
8,4 |
147,6 |
| 3 |
88,6 |
60 |
10,9 |
159,5 |
| 4 |
95,7 |
60 |
8,3 |
164 |
| 5 |
98,4 |
60 |
3,2 |
161,6 |
| 6 |
97 |
60 |
-1,7 |
155,3 |
| 7 |
93,2 |
60 |
-4,4 |
148,8 |
| 8 |
89,3 |
60 |
-4,6 |
144,7 |
| 9 |
86,8 |
60 |
-2,9 |
143,9 |
| 10 |
86,3 |
60 |
-0,6 |
145,7 |
| 11 |
87,4 |
60 |
1,3 |
148,7 |
| 12 |
87,2 |
60 |
2,1 |
149,3 |
| 13 |
89,6 |
60 |
0,4 |
150 |
| 14 |
90 |
60 |
0,5 |
150,5 |
| 15 |
90,3 |
60 |
0,4 |
150,7 |
| 16 |
90,4 |
60 |
0,1 |
150,5 |
| 17 |
90,3 |
60 |
-0,1 |
150,2 |
| 18 |
90,1 |
60 |
-0,2 |
149,9 |
| 19 |
89,9 |
60 |
-0,2 |
149,7 |
| 20 |
89,8 |
60 |
-0,1 |
149,7 |
| 21 |
89,8 |
60 |
0 |
149,8 |
В периоде 1 национальный доход увеличился на величину прироста автономных инвестиций (ΔI1
a = 12) и составил 132. Данное обстоятельство привело в периоде 2 к увеличению объема совокупного потребления до 79,2 и к появлению индуцированных инвестиций в размере 8,4. Это означает, что здесь действуют и мультипликатор и акселератор.
В периоде 3 объем производных инвестиций достиг максимального значения (Itин
= 10,9), поскольку в предыдущем периоде произошел максимальный прирост национального дохода (Δу2
= y2
- y1
= 15,6). В дальнейшем (периоды 4 и 5) величина индуцированных капиталовложений уменьшалась из-за падения темпов прироста национального дохода в периодах 3 и 4. Более того, начиная с периода 6, производные инвестиции приняли отрицательное значение. Это объясняется снижением уровня дохода в предшествующем периоде (I6ин
= -1,7, поскольку Δу5
= y5
- y4
= 15,6). Совокупное потребление продолжало возрастать и в периоде 5 достигло максимальной величины (98,4), поскольку в предыдущем периоде национальный доход был максимален (164). В дальнейшем, с 6 по 10 период происходило снижение объема потребления.
Табличные данные отражают затухающие колебания национального дохода, совокупного потребления и производных инвестиций. Если бы действовал только один мультипликатор, то при данном варианте автономного инвестирования система устремилась бы к новому равновесному состоянию. Подключение акселератора привело к волнообразным колебаниям экономической системы.
В данном числовом примере мультипликатор и акселератор фигурируют в качестве постоянных величин. В реальной экономической жизни не существует постоянных коэффициентов мультипликации и акселерации в силу действия таких переменных факторов, как научно-технический прогресс, сальдо торгового баланса, товарные запасы, степень монополизации производства и т. д.
1.3 Линейные конечно-разностные уравнения и их применение в экономике
Динамика объектов различной природы часто описывается уравнениями вида
xt
= F
(xt
-1
, xt
-2
, ... , xt
-n
),(7)
связывающими состояние объекта xt
в любой момент времени t
с состояниями в предшествующие моменты времени. Решение уравнения (7) n
-го порядка определено однозначно, если заданы n
так называемых начальных условий. Обычно в качестве начальных условий рассматриваются значения xt
при t
= 0, 1,..., n
- 1.
Подставляя начальные значения xn
-1
, ... , x
1
, x
0
и t
= n
в качестве аргументов функции в правой части (7), находим xn
; используя найденное значение и подставляя теперь xn
, xn
-1
, ... , x
2
x
1
и t
= n
+ 1 в качестве аргументов функции, находим xn
+1
, и т.д. Процесс может быть продолжен до тех пор, пока не будут исчерпаны все представляющие интерес значения t
.
В модели экономических циклов Самуэльсона-Хикса используются конечно-разностные уравнения вида xt
= a
1
xt
-1
+ a
2
xt
-2
+ f
(t
) - линейные конечно-разностные уравнения второго порядка, являющиеся частным видом уравнения (7). Они называются однородными, еслиf
(t
) = 0 при любых t
, неоднородными - в противном случае. И для нахождения, и для исследования свойств решения однородного уравнения
xt
= a
1
xt
-1
+ a
2
xt
-2 ,
(8)
используется так называемое характеристическое уравнение
 - a
1 - a
1 - a
2 ,
(9)
- a
2 ,
(9) 
Обозначим его корни  1
, 1
,  2
и запишем 2
и запишем

В теории конечно-разностных уравнений[4]
доказывается, что при  1 1
  2
решение уравнения (8) описывается равенством 2
решение уравнения (8) описывается равенством
 , (10) , (10)
где A
1
и A
2
- постоянные, определяемые начальными условиями.
Если же  1
= 1
=  2
= 2
=  , то решение имеет вид , то решение имеет вид
 , (11) , (11)
Решение уравнения (8) зависит от значения дискриминанта  характеристического уравнения (9). характеристического уравнения (9).
Рассмотрим возникающие при этом случаи.1. D
> 0. Характеристическое уравнение имеет два различных вещественных корня. Решение описывается равенством (10); если оба корня положительны, то обе компоненты решения - монотонные геометрические прогрессии. Если имеются отрицательные корни, то каждому из них отвечает знакочередующаяся составляющая решения (10).2. D
= 0. Характеристическое уравнение имеет совпадающие вещественные корни, и решение имеет вид (11).
3. D
< 0. Характеристическое уравнение имеет пару сопряженных комплексных корней:  1,2
= 1,2
=   i i
 . .
Равенство (10) при этом справедливо, но неудобно для использования, так как вещественный процесс при этом описывается как сумма комплексных составляющих. Более удобную форму решения можно получить, используя тригонометрическое представление корней:  1,2
= g
(cos 1,2
= g
(cos  sin sin ), где ), где  Такое представление позволяет описать решение уравнения (8) равенством Такое представление позволяет описать решение уравнения (8) равенством
 , (12) , (12)
где B
1
и B
2
- постоянные, определяемые начальными условиями.
Таким образом, при D
< 0 решение носит характер колебаний, амплитуда которых возрастает (при g
> 1) или убывает (при g
< 1);
Решение уравнения (8) называют равновесным, если значение xt
не изменяется во времени. Подстановкой в уравнение (8) можно убедиться, что xt
= 0 есть равновесное решение. Равновесное решение называется устойчивым, если xt
 0 при t 0 при t
  ; в противном случае оно называется неустойчивым. Равенства (10) и (11) показывают, что решение будет устойчивым в том и только в том случае, если оба корня характеристического уравнения по модулю меньше единицы. В случае D
< 0 условию устойчивости соответствует g
< 1, так как ; в противном случае оно называется неустойчивым. Равенства (10) и (11) показывают, что решение будет устойчивым в том и только в том случае, если оба корня характеристического уравнения по модулю меньше единицы. В случае D
< 0 условию устойчивости соответствует g
< 1, так как  при этом необходимым и достаточным условием устойчивости является a
2
> -1. По теореме Виета при этом необходимым и достаточным условием устойчивости является a
2
> -1. По теореме Виета  1 1
 2
= -a
2
, так что условие a
2
> -1 необходимо и в случае D
> 0, но здесь оно не является достаточным. Система неравенств 2
= -a
2
, так что условие a
2
> -1 необходимо и в случае D
> 0, но здесь оно не является достаточным. Система неравенств

дает необходимое и достаточное условие устойчивости для данного случая. Для этого требуется, чтобы выполнялось неравенство 
Систему можно заменить одним неравенством

Объединяя все полученные результаты, условие устойчивости можно представить в виде двойного неравенства
 ,(13) ,(13)
Уравнение модели экономических циклов Самуэльсона-Хикса имеет вид уравнения (8), при этом 
Заметим, что Cy
 0 и 0 и   0 в силу экономического содержания этих параметров. Согласно теореме Виета, 0 в силу экономического содержания этих параметров. Согласно теореме Виета,
 ,(14) ,(14)
Условие D
= 0, разделяющее колебательные и неколебательные решения, теперь имеет вид

При  характеристическое уравнение имеет вещественные корни. Из неотрицательности параметров Cy
и характеристическое уравнение имеет вещественные корни. Из неотрицательности параметров Cy
и  и равенств (14) следует, что оба корня неотрицательны и обе компоненты решения (10) изменяются монотонно. При и равенств (14) следует, что оба корня неотрицательны и обе компоненты решения (10) изменяются монотонно. При  решение носит колебательный характер. решение носит колебательный характер.
Условие устойчивости (13) теперь принимает вид

т.е. представляет собой систему неравенств

На рис. 4. устойчивому движению соответствуют области I (монотонное движение) и II (колебательное движение). Неустойчивому движению соответствуют области III (колебательное движение) и IV (монотонное). Области V соответствуют синусоидальные колебания с постоянной амплитудой.
 [5] [5]
Рис. 4. Стилизованные фазы экономического цикла
Разностные уравнения играют большую роль в экономической теории. Многие экономические законы доказывают с помощью именно этих уравнений, они используются в тех случаях, когда запаздывание оказывает существенное влияние на рассматриваемые процессы. В социально – экономических науках в целях простоты модели, связанные с запаздыванием, записывают в виде разностных уравнений, то есть в виде уравнений с дискретным временем. Наиболее широкое распространение разностные уравнения в экономической теории
Применение разностных уравнений в экономике представлено в моделях:
1. Модель рынка с запаздыванием сбыта.
2. Рыночная модель с запасами.
3. Динамическая модель Леонтьева.
4. Модель экономического цикла Самуэльсона – Хикса.
ГЛАВА 2. МОДЕЛЬ САМУЭЛЬСОНА-ХИКСА И ЕЕ ПРИМЕНЕНИЕ
2.1 Модель Самуэльсона-Хикса
Модель Самуэльсона-Хикса включает в себя только рынок благ, и поэтому уровень цен и ставка процента предполагаются неизменными; объем предложения благ совершенно эластичен.
Объем потребления домашних хозяйств в текущем периоде зависит от величины их дохода в предшествующем периоде
Ct
= Ca,t
+ Cy
yt
-1
,
где Ca
- автономное потребление.
Предприниматели осуществляют автономные инвестиции, объем которых при заданной ставке процента фиксирован, и индуцированные инвестиции, зависящие от прироста совокупного спроса в предшествующем периоде
It
= Ia,t
+  (yt
-1
- yt
-2
). (yt
-1
- yt
-2
).
На рынке благ установится динамическое равновесие, если
 ,(15) ,(15)
гдеAt
= С
a
,t
+ Ia
,t
.
Уравнение (15) является неоднородным конечно-разностным уравнением второго порядка, характеризующим динамику национального дохода во времени.
Уравнение (9.1) является неоднородным конечно-разностным уравнением второго порядка, характеризующим динамику национального дохода во времени.
При фиксированной величине автономных расходов (At
= A
= const) в экономике достигается динамическое равновесие, когда объем национального дохода стабилизируется на определенном уровне  , т.е.yt
= yt
-1
= yt
-2
= ... = yt-n
= , т.е.yt
= yt
-1
= yt
-2
= ... = yt-n
=  , где n
- число периодов с неизменной величиной автономных расходов. , где n
- число периодов с неизменной величиной автономных расходов.
Из уравнения (15) следует, что  = A
/(1 - Cy
). = A
/(1 - Cy
).
Посмотрим, какова будет динамика национального дохода, если в состоянии динамического равновесия изменится величина автономного спроса.
 Освободимся от неоднородности в уравнении (15). Значения yt
и Освободимся от неоднородности в уравнении (15). Значения yt
и  удовлетворяют равенству (15), поэтому можно записать следующее однородное конечно-разностное уравнение второй степени с постоянными коэффициентами: удовлетворяют равенству (15), поэтому можно записать следующее однородное конечно-разностное уравнение второй степени с постоянными коэффициентами:
 , , (16) (16)
где  yt yt
 yt
- yt
-  . .
Так как yt
=  + yt
, то направление изменения yt
определяется направлением изменения + yt
, то направление изменения yt
определяется направлением изменения  yt
. yt
.
Из теории решения дифференциальных и конечно-разностных уравнений следует, что характер изменения  yt
зависит от значения дискриминанта характеристического уравнения. Поскольку в данном случае дискриминант равен (Cy
+ yt
зависит от значения дискриминанта характеристического уравнения. Поскольку в данном случае дискриминант равен (Cy
+  )2
- 4 )2
- 4 , то динамика национального дохода зависит от предельной склонности к потреблению, определяющей величины мультипликатора и акселератора. , то динамика национального дохода зависит от предельной склонности к потреблению, определяющей величины мультипликатора и акселератора.
Если (Cy
+  )2
- 4 )2
- 4 > 0, то изменение yt
происходит монотонно; при (Cy
+ > 0, то изменение yt
происходит монотонно; при (Cy
+  )2
- 4 )2
- 4 < 0 оно будет колебательным. Следовательно, график функции < 0 оно будет колебательным. Следовательно, график функции  , изображенный на рис. 5, отделяет множество сочетаний Cy
, , изображенный на рис. 5, отделяет множество сочетаний Cy
,  , обеспечивающих монотонное изменение yt
, от множества комбинаций из значений Cy
, , обеспечивающих монотонное изменение yt
, от множества комбинаций из значений Cy
,  , приводящих к колебаниям yt
. , приводящих к колебаниям yt
.
Устремляется ли значение yt
к некоторой конечной величине или уходит в бесконечность, зависит от значения последнего слагаемого характеристического уравнения. Если  < 1, то равновесие установится на определенном уровне. При < 1, то равновесие установится на определенном уровне. При  > 1 нарушенное 1 раз равновесие больше не восстановится. Когда > 1 нарушенное 1 раз равновесие больше не восстановится. Когда  = 1 , тогда значение yt
будет колебаться с постоянной амплитудой. = 1 , тогда значение yt
будет колебаться с постоянной амплитудой.
 [6] [6]
Рис. 5. Четыре областисочетаний Cy
, 
В результате все множество сочетаний Cy
и  оказалось разделенным на пять областей, как это показано на рис. 5. Если значения Cy
и оказалось разделенным на пять областей, как это показано на рис. 5. Если значения Cy
и  указывают на область I, то после нарушения равновесия в результате изменения автономного спроса значение yt
монотонно устремится к новому равновесному уровню указывают на область I, то после нарушения равновесия в результате изменения автономного спроса значение yt
монотонно устремится к новому равновесному уровню  При значениях Cy
и При значениях Cy
и  , находящихся в области II, национальный доход достигнет нового равновесного уровня, пройдя через затухающие колебания. Сочетания значений Cy
и , находящихся в области II, национальный доход достигнет нового равновесного уровня, пройдя через затухающие колебания. Сочетания значений Cy
и  , расположенные справа от перпендикуляра, опущенного из точки B
на ось абсцисс, соответствуют нестабильному равновесию. Когда сочетания значений Cy
, , расположенные справа от перпендикуляра, опущенного из точки B
на ось абсцисс, соответствуют нестабильному равновесию. Когда сочетания значений Cy
,  указывают на область III, тогда динамика yt
приобретает характер взрывных колебаний. Комбинации значений Cy
, указывают на область III, тогда динамика yt
приобретает характер взрывных колебаний. Комбинации значений Cy
,  в области IV приводят к тому, что после нарушения равновесия yt
монотонно устремляется в бесконечность. И наконец, если акселератор равен единице, то при любом значении предельной склонности к потреблению в случае нарушения равновесия возникают равномерные незатухающие колебания yt
. в области IV приводят к тому, что после нарушения равновесия yt
монотонно устремляется в бесконечность. И наконец, если акселератор равен единице, то при любом значении предельной склонности к потреблению в случае нарушения равновесия возникают равномерные незатухающие колебания yt
.
2.2 Практическое применение модели Самуэльсона-Хикса
Пример
Заданы функция потребления домашних хозяйств: Ct
= 50 + 0,8yt
-1
и функция спроса предпринимателей на автономные и индуцированные инвестиции: It
= 250 +  (yt
-1
- yt
-2
). В течение некоторого времени до периода t
0
включительно экономика находится в динамическом равновесии при спросе предпринимателей на автономные инвестиции в объеме 250 ден. ед. Это значит, что в каждом периоде производилось 1500 ед. благ, из которых 50 + 0,8·1500 = 1250 потребляют домашние хозяйства. С периода t
1
предприниматели решили, что объем автономных инвестиций должен равняться 350 ден. ед. Как в результате реализации этого решения будет меняться величина совокупного спроса (следовательно, и национального дохода) при четырех различных сочетаниях Cy
, (yt
-1
- yt
-2
). В течение некоторого времени до периода t
0
включительно экономика находится в динамическом равновесии при спросе предпринимателей на автономные инвестиции в объеме 250 ден. ед. Это значит, что в каждом периоде производилось 1500 ед. благ, из которых 50 + 0,8·1500 = 1250 потребляют домашние хозяйства. С периода t
1
предприниматели решили, что объем автономных инвестиций должен равняться 350 ден. ед. Как в результате реализации этого решения будет меняться величина совокупного спроса (следовательно, и национального дохода) при четырех различных сочетаниях Cy
,  , представленных на рис. 9.4 точками a
(Cy
= 0,8; , представленных на рис. 9.4 точками a
(Cy
= 0,8;  = 0,25), b
(Cy
= 0,8; = 0,25), b
(Cy
= 0,8;  = 0,75), c
(Cy
= 0,8; = 0,75), c
(Cy
= 0,8;  = 1,2) и d
(Cy
= 0,8; = 1,2) и d
(Cy
= 0,8;  = 2,3), показано в табл. 9.1-9.4. = 2,3), показано в табл. 9.1-9.4.

Рис. 6. Динамика национального дохода после изменения автономного спроса при различных сочетаниях Cy
, 
Таблица 2.1Динамика национального дохода при Cy
= 0,8;  = 0,25 = 0,25
| t |
C |
Ia
|
Iin
|
y |
| 0 |
1250 |
250 |
0 |
1500 |
| 1 |
1250 |
350 |
0 |
1600 |
| 2 |
1330 |
350 |
25 |
1705 |
| 3 |
1414 |
350 |
26,25 |
1790,3 |
| 4 |
1482,2 |
350 |
21,31 |
1853,5 |
| 5 |
1532,8 |
350 |
15,82 |
1898,6 |
| 6 |
1568,9 |
350 |
11,28 |
1930,2 |
| 7 |
1594,1 |
350 |
7,89 |
1952,0 |
| 8 |
1611,6 |
350 |
5,46 |
1967,1 |
| 9 |
1623,7 |
350 |
3,76 |
1977,4 |
| 10 |
1631,9 |
350 |
2,59 |
1984,5 |
| 11 |
1637,6 |
350 |
1,77 |
1989,4 |
| 12 |
1641,5 |
350 |
1,22 |
1992,7 |
| 13 |
1644,2 |
350 |
0,83 |
1995,0 |
| 14 |
1646,0 |
350 |
0,57 |
1996,6 |
| 15 |
1647,3 |
350 |
0,39 |
1997,7 |
| 16 |
1648,1 |
350 |
0,27 |
1998,4 |
| 17 |
1648,7 |
350 |
0,18 |
1998,9 |
| 18 |
1649,1 |
350 |
0,13 |
1999,2 |
| 19 |
1649,4 |
350 |
0,09 |
1999,5 |
| 20 |
1649,6 |
350 |
0,06 |
1999,6 |
| ... |
... |
... |
... |
... |
Таблица 2.2Динамика национального дохода при Cy
= 0,8;  = 0,75 = 0,75
| t |
C |
Ia
|
Iin
|
y |
| 0 |
1250 |
250 |
0 |
1500 |
| 1 |
1250 |
350 |
0 |
1600 |
| 2 |
1330 |
350 |
75 |
1755 |
| 3 |
1454 |
350 |
116,3 |
1920,3 |
| 4 |
1586,2 |
350 |
123,9 |
2060,1 |
| 5 |
1698,1 |
350 |
104,9 |
2153,0 |
| 6 |
1772,4 |
350 |
69,7 |
2192,1 |
| 7 |
1803,7 |
350 |
29,3 |
2183,0 |
| 8 |
1796,4 |
350 |
-6,8 |
2139,5 |
| 9 |
1761,6 |
350 |
-32,6 |
2079,0 |
| 10 |
1713,2 |
350 |
-45,4 |
2017,9 |
| 11 |
1664,3 |
350 |
-45,9 |
1968,4 |
| 12 |
1624,7 |
350 |
-37,1 |
1937,6 |
| 13 |
1600,1 |
350 |
-23,1 |
1927,0 |
| 14 |
1591,6 |
350 |
-8,0 |
1933,7 |
| 15 |
1596,9 |
350 |
5,0 |
1951,9 |
| 16 |
1611,5 |
350 |
13,7 |
1975,2 |
| 17 |
1630,2 |
350 |
17,5 |
1997,6 |
| 18 |
1648,1 |
350 |
16,8 |
2014,9 |
| 19 |
1662,0 |
350 |
13,0 |
2024,9 |
| 20 |
1669,9 |
350 |
7,5 |
2027,4 |
| 21 |
1671,9 |
350 |
1,9 |
2023,8 |
| 22 |
1669,1 |
350 |
-2,7 |
2016,3 |
| 23 |
1663,1 |
350 |
-5,6 |
2007,5 |
| 24 |
1656,0 |
350 |
-6,7 |
1999,3 |
| 25 |
1649,5 |
350 |
-6,1 |
1993,4 |
| 26 |
1644,7 |
350 |
-4,5 |
1990,2 |
| 27 |
1642,2 |
350 |
-2,4 |
1989,8 |
| 28 |
1641,8 |
350 |
-0,3 |
1991,5 |
| 29 |
1643,2 |
350 |
1,3 |
1994,5 |
| 30 |
1645,6 |
350 |
2,2 |
1997,9 |
| ... |
... |
... |
... |
... |
Таблица 2.3Динамика национального дохода при Cy
= 0,8;  = 1,2 = 1,2
| t |
C |
Ia
|
Iin
|
y |
| 0 |
1250 |
250 |
0 |
1500 |
| 1 |
1250 |
350 |
0 |
1600 |
| 2 |
1330 |
350 |
120 |
1800 |
| 3 |
1490 |
350 |
240 |
2080 |
| 4 |
1714 |
350 |
336 |
2400 |
| 5 |
1970 |
350 |
384 |
2704 |
| 6 |
2213,2 |
350 |
364,8 |
2928 |
| 7 |
2392,4 |
350 |
268,8 |
3011,2 |
| 8 |
2459,0 |
350 |
99,8 |
2908,8 |
| 9 |
2377,0 |
350 |
-122,9 |
2604,2 |
| 10 |
2133,3 |
350 |
-365,6 |
2117,8 |
| 11 |
1744,2 |
350 |
-583,7 |
1510,5 |
| 12 |
1258,4 |
350 |
-728,7 |
879,7 |
| 13 |
753,8 |
350 |
-756,9 |
346,9 |
| 14 |
327,5 |
350 |
-639,5 |
38,0 |
| 15 |
80,4 |
350 |
-370,6 |
59,89 |
| 16 |
97,8 |
350 |
26,1 |
474,0 |
| 17 |
429,2 |
350 |
497,0 |
1276,2 |
| 18 |
1071,0 |
350 |
962,7 |
2383,6 |
| 19 |
1956,9 |
350 |
1328,9 |
3635,8 |
| 20 |
2958,7 |
350 |
1502,6 |
4811,3 |
| 21 |
3899,0 |
350 |
1410,5 |
5659,6 |
| 22 |
4577,7 |
350 |
1017,9 |
5945,6 |
| 23 |
4806,5 |
350 |
343,2 |
5499,7 |
| 24 |
4449,8 |
350 |
-535,1 |
4264,7 |
| 25 |
3461,8 |
350 |
-1482,0 |
2329,8 |
| ... |
... |
... |
... |
Таблица 2.4Динамика национального дохода при Cy
= 0,8;  = 2,3 = 2,3
| t |
C |
Ia
|
Iin
|
y |
| 0 |
1250 |
250 |
0 |
1500 |
| 1 |
1250 |
350 |
0 |
1600 |
| 2 |
1330 |
350 |
230 |
1910 |
| 3 |
1578 |
350 |
713 |
2641 |
| 4 |
2162,8 |
350 |
1681,3 |
4194,1 |
| 5 |
3405,3 |
350 |
3572,1 |
7327,4 |
| ... |
... |
... |
... |
... |
ЗАКЛЮЧЕНИЕ
Рассмотренная модель Самуэльсона-Хикса дает возможность сделать выводы о причинах и факторах возникновения эндогенных (самогенерирующихся) циклических колебаний в экономической системе. Несмотря на абстрактный характер допущений, принимаемых в моделях колебательных процессов, нельзя не отметить строгость и прозрачность выводов, получаемых на основе анализа.В теоретических исследованиях экономической динамики, которые могут быть отнесены к традиционным направлениям экономической науки, наибольшее внимание уделяется инвестиционному поведению. Последнее представляется в виде определенной зависимости между размерами инвестиций и характеристиками состояния экономической системы - прибылью, доходом, занятостью, ставкой процента и т.д.
Однако реальные колебательные процессы с большой условностью можно считать циклическими, имея в виду лишь последовательное чередование стадий цикла, а не строгую периодичность этих стадий. Чтобы дать более реалистическое описание таких процессов, необходимо создать модели, позволяющие выявить иррегулярную, хаотическую динамику экономических переменных. В последнее время появились работы, в которых делаются попытки построения плотность детерминированных динамических моделей с хаотическим поведением траекторий.Последовательные теоретические построения в данной области должны включать прежде всего объяснение внутренних экономических механизмов развития, выявление движущих сил, поведенческих мотивов и средств реализации изменений в экономических системах.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
Учебники и учебные пособия
1.Красс М.С. Математика для экономических специальностей./Учебник. М.:ИНФРА-М, 1998.
2. Гальперин В.М. Макроэкономика. СПб.: Экономическая школа, 1997.
3. Станковская И.К., И.А. Стрелец. Экономическая теория: учебник –3-е изд., испр. – М.:Эксмо, 2007. –448 с.
4. Боярский А.Я. Математика для экономистов. М.: Госстатиздат, 1961.
5. Кремер Н.Ш., Путко Б.А., Тришнин И.М., Фридман М.Н. Высшая математика для экономистов./ Учебное пособие для вузов./ Под ред. проф. Н.Ш. Кремера. М.: Банки и биржи, ЮНИТИ, 1997. 439 с.
6. Крушевский А.В. Справочник по экономико-математическим моделям и методам. Киев: Техника, 1982.
Источники из Интернета
1.http://www.spbki.ru/rus/parts/microeconomics
2.job.finec.ru/rus/parts/macroeconomics/chap9/9_1/9_1.html
[1]
Гальперин В.М. Макроэкономика. СПб.: Экономическая школа, 1997.
[2]
Гальперин В.М. Макроэкономика. СПб.: Экономическая школа, 1997.
[3]
Красс М.С. Математика для экономических специальностей./Учебник. М.:ИНФРА-М, 1998.
[4]
http://www.spbki.ru/rus/parts/macroeconomics/chap9/gl9.html
[5]
job.finec.ru/rus/parts/macroeconomics/chap9/9_1/9_1.html
[6]
http://www.spbki.ru/rus/parts/macroeconomics/chap9/9_2/9_2_1.html
|