СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. КРАТКОЕ ОПИСАНИЕ ООО «ДУБРОВЧАНКА+»
1.1 Историческая справка
1.2 Характеристика предприятия
1.3 Организационная структура и статистические данные
2. ПРИМЕНЕНИЕ МЕТОДОВ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ РЕШЕНИИ ЭКОНОМИЧЕСКИХ ЗАДАЧ
2.1 Понятие линейного программирования
2.2 Построение и решение ЭММ на примере ООО «Дубровчанка+»
3. ПРИМЕНЕНИЕ ТЕОРИИ ТРАНСПОРТНОЙ ЗАДАЧИ К РАБОТЕ ООО «ДУБРОВЧАНКА+»
3.1 Сущность транспортной задачи
3.2 Решение транспортной задачи на примере ООО «Дубровчанка+»
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
Различные технико-экономические и экономические производственные задачи, начиная от оптимальной загрузки станка и раскройки стального листа или полотна ткани до анализа межотраслевого баланса и оценки темпов роста экономики страны в целом, приводят к необходимости решения тех или иных задач линейного программирования.
На сегодняшний день это является важным инструментом экономического анализа: позволяет получить четкое представление о состоянии предприятия, охарактеризовать и количественно описать его внутреннюю структуру и внешние связи. Таким образом, экономико-математическое моделирование работы предприятия, фирмы, основанное на анализе его деятельности, должно обогащать этот анализ результатами и выводами, полученными после решения соответствующих задач.
Часто эксперимент с математической моделью может заменить реальный эксперимент, который либо слишком дорог, либо невозможен по тем или иным причинам. Все это и дает весомую актуальность применению задач линейного программирования в современных экономических условиях и данной курсовой работе как его частному случаю.
Целью работы стали систематизация теоретических данных по выбранной теме и их применение на конкретном предприятии. Для достижения этой цели были поставлены следующие задачи:
- рассмотреть сущность задач линейного программирования;
- выявить основные методы линейного программирования при решении экономических задач, изучить алгоритм построения экономико-математических моделей;
- применить теоретические положения построения ЭММ и транспортной задачи к статистическим данным ООО «Дубровчанка+», а также их решения в виде расчета плана максимизации прибыли и минимизации расходов на перевозку продукции потребителям.
Исходя из этого, объектом исследования в рамках курсовой работы стала область применения методов линейного программирования при решении экономических задач, а предметом – ее применение на конкретном предприятии.
Все это и дало обоснование для следующего структурирования работы. Курсовая работа содержит введение, где дается обоснование актуальности выбранной для исследования темы, формируются цели, задачи, объект и предмет исследования, отражены структура работы, а также теоретическая и информационная база, использованная при ее написании.
Основная часть данной курсовой работы, решающая поставленные цели и задачи, состоит из двух разделов. Так, первый из них «Краткое описание ООО «Дубровчанка+» включает в себя при этом подразделы «Историческая справка», «Характеристика предприятия» и «Организационная структура и статистические данные».
Второй раздел носит название «Применение методов линейного программирования при решении экономических задач» и включает в себя подразделы «Понятие линейного программирования» и «Построение и решение ЭММ на примере ООО «Дубровчанка+».
Третий «Применение теории транспортной задачи к работе ООО «Дубровчанка+» раскрывает понятие транспортной задачи, методику ее построения и решения в подразделе «Сущность транспортной задачи» и описывает механизм его применения на конкретном предприятии.
В заключении освещаются основные теоретические положения по исследуемой теме, а также обобщаются результаты проведенной работы.
Информационной базой для написания курсовой работы послужили популярные учебные пособия отечественных авторов: Алесинской Т.В. - Учебное пособие по решению задач по курсу «Экономико-математические методы и модели», А.И. Орлова – «Теория принятия решений», «Исследование операций в экономике» под редакцией Н.Ш. Кремера и другие.
1. КРАТКОЕ ОПИСАНИЕ ООО «ДУБРОВЧАНКА+»
1.1 Историческая справка
ООО «Дубровчанка+» является наследником одного из старейших предприятий Пензенской области - Городищенского деревоперерабатывающего завода, основанного в 1939 году.
История завода начиналась с работы объединения кустарей и ремесленников г. Городище в разных по своему профилю промартелях. Так, еще до Великой Отечественной войны в шорном и сапожном цехах работало лишь 18 человек. В годы войны к ним прибавились валяльный, кожевенный, жестяной и столярный цеха.
17 ноября 1971 года решением Пензенского Облисполкома предприятие было переименовано в «Городищенский деревоперерабатывающий завод» (ДОЗ), именно с этого периода начинается его интенсивное строительство, а численность занятых на производстве рабочих достигает более 700 человек.
Основной специализацией предприятия стал выпуск мебели различного назначения и мебельных деталей. Гарнитуры для кухни, выпускаемые в Городище, были востребованы как среди населения Пензенской, так и других областей. А полумягким стульям и табуретам был присвоен в свое время государственный Знак качества.
Однако помимо производства мебели, ДОЗ занимался лесоразработками, ежегодно заготавливая 18 тысяч кубометров древесины, изготовлением кирпича и резной сувенирной продукции.
С 2001 года после технического перевооружения предприятия и оснащения цехов современными деревообрабатывающими станками зарубежного и отечественного производства предприятие приступило к выпуску качественной мебели современного дизайна и высокой экологической чистоты, пиломатериалов и поганажа.
1.2 Характеристика предприятия
На сегодняшний день ООО «Дубровчанка +» располагается на территории в 19 гектаров, обладает мебельными цехами общей площадью 8500 квадратных метров, собственным лесозаготовительным, лесопильным и сушильным участками. Заготовка ежегодно арендуемого леса позволяет в полной мере обеспечивать производство мебели из отборной древесины, производить пиломатериалы хвойных и лиственных пород на продажу. За последние годы на предприятии также налажено производство погонажа (вагонки, половой рейки, блок-хауса).
Серийно изготавливаемая продукция представлена наборами мебели для кухни с фасадами из пластика и массива древесины, угловыми скамьями, табуретками, обеденными столами, кроватями и другими изделиями[1]
. Помимо серийных моделей, организовано производство мебели по индивидуальным проектам.
Удобное географическое расположение предприятия позволяет производить отгрузку продукции автомобильным и железнодорожным транспортом в любую точку России, ближнего и дальнего зарубежья. Кроме всего этого, для заказчиков и покупателей подмосковного и близлежащих к нему регионов недавно открыто представительство в Москве, так же полно демонстрирующее всю гамму мебельной продукции.
Основной упор в развитии предприятия сейчас делается на поддержание и развитие надежных партнерских отношений с заказчиками, внедрение новых технологий с целью постоянного совершенствования качества и снижения стоимости выпускаемой продукции, расширение ассортимента и разработку новых моделей мебельной продукции, отвечающих высоким требованиям покупателей.
Таблица 1
Основные виды продукции ООО «Дубровчанка +»
| Наименование изделия
|
Габаритные размеры, мм
|
Ед.изм.
|
| Кухня "Добровчанка-Н8" (угловая, без раковины, фасад - массив, постформинг) |
2400*1600 |
к-т. |
| Шкаф навесной 2-х дверный (фасад - массив) |
800*320*720 |
шт. |
| Шкаф-стол однодверный (фасад - массив) |
400*600*850 |
шт. |
| Шкаф навесной однодверный стекло (фасад - массив) |
400*320*420 |
шт. |
| Шкаф-стол с ящиком на 400 (фасад - массив) |
400*600*850 |
шт. |
| Шкаф-стол на 800 (фасад - массив) |
800*600*850 |
шт. |
| Шкаф-стол под мойку (без крышки, без раковины, массив) |
800*600*850 |
шт. |
| Шкаф навесной однодверный (фасад - массив) |
400*320*720 |
шт. |
| Шкаф-стол угловой (фасад - массив) |
800*800*850 |
шт. |
| Шкаф навесной угловой (фасад - массив) |
600*600*720 |
шт. |
| Шкаф навесной открытый |
200*300*720 |
шт. |
| Шкаф навесной 2-х дверный, массив, стекло |
800*320*720 |
шт. |
| Кухня "Дубровчанка-Н3" (без раковины, фасад - массив, постформинг) |
2000*600*2085 |
к-т. |
| Стол обеденный, пластик |
800*600*750 |
шт. |
| Стол обеденный "Ладога", пластик |
110*600*750 |
шт. |
| Стол обеденный из массива |
1200*670*750 |
шт. |
| Стол обеденный раскладной, пластик |
800*600(1200*800)*750 |
шт. |
| Табурет кухонный, массив |
320*320*450 |
шт. |
| Табурет кухонный, пластик |
320*320*450 |
шт. |
| Табурет кухонный, мягкий |
320*320*450 |
шт. |
| Скамья угловая |
1540*1130*800 |
шт. |
| Кровать подростковая 2-х ярусная |
1985*750*1650 |
шт. |
| Кроватка детская, массив |
1255*670*900 |
шт. |
| Комод из массива |
800*560*850 |
шт. |
| Прикроватная тумбочка |
505*400*555 |
шт. |
| Стул мягкий (шинил) |
шт. |
| Матрац ватный (кровать подр. 2-х ярусная) |
шт. |
| Матрац ватный (кроватка детская) |
шт. |
| П/материал хвойных пород необрезной |
м3
|
| П/материал лиственных пород необрезной |
м3
|
| Евровагонка |
м3
|
1.3 Организационная структура и статистические данные
Организационная структура предприятия представлена на схеме:

В настоящее время ООО «Дубровчанка+» располагается на территории в 19 га, обладает мебельными цехами общей площадью 8500 квадратных метров, лесозаготовительным, лесопильным и сушильным участками. Здесь производится более 40 видов мебельной продукции, на предприятии занято порядка 120 человек со средней заработной платой 6000-7000 рублей. Средний объем производства составляет около 1000 единиц продукции в месяц, которая реализуется как среди потребителей Пензенской области, так и других регионов: Самарской, Саратовской, Тамбовской, Московской и других областей. Объемы лесозаготовки для собственного производства и к реализации составляют примерно 10 000-13000 кубометров древесины в год.
2. ПРИМЕНЕНИЕ МЕТОДОВ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ РЕШЕНИИ ЭКОНОМИЧЕСКИХ ЗАДАЧ
2.1 Понятие задачи линейного программирования
Временем рождения линейного программирования принято считать 1939г., когда была напечатана брошюра Л.В. Канторовича «Математические методы организации и планирования производства» [2]. Поскольку методы, изложенные им, были мало пригодны для ручного счета, а быстродействующих вычислительных машин в то время не существовало, работа Л.В. Канторовича осталась почти не замеченной. Свое второе рождение линейное программирование получило в начале пятидесятых годов с появлением ЭВМ. Тогда началось всеобщее увлечение линейным программированием, вызвавшее в свою очередь развитие других разделов математического программирования.
Таким образом, линейное программирование - область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной (целевой) функции многих переменных при наличии линейных ограничений, т. е. равенств или неравенств, связывающих эти переменные [1].
Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид:




В этом случае говорят, что задача представлена в канонической форме. При этом система линейных уравнений и неравенств, определяющая допустимое множество решений задачи W, называется системой ограничений задачи линейного программирования, а линейная функция f(Х) называется целевой функцией или критерием оптимальности. В частном случае, если I= Ш, то система состоит только из линейных неравенств, а если I= M, то – из линейных уравнений.
Итак, характерные черты задач линейного программирования следующие:
1) показатель оптимальности f(X) представляет собой линейную функцию от элементов решения X = (x1
, x2
, ..., xn
);
2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.
Любую задачу линейного программирования можно свести к задаче в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот.
Правило приведения задачи линейного программирования к каноническому виду состоит в следующем:
1) если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции;
2) если в ограничениях правая часть отрицательна, то следует умножить это ограничение на -1;
3) если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства;
4) если некоторая переменная xk
не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными:  , где , где  - свободный индекс,
- свободный индекс,  . .
При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели таких свойств, как пропорциональность и аддитивность. Пропорциональностьозначает, что вклад каждой переменной в целевой функции и общий объем потребления соответствующих ресурсов должен быть прямо пропорционаленвеличине этой переменной. Аддитивностьозначает, что целевая функция и ограничения должны представлять собой сумму вкладов от различных переменных [4].
Исходя из отмеченных выше особенностей задач линейного программирования, можно наметить следующую общую схему формирования экономико-математической модели:
- выбор некоторого числа переменных величин, заданием числовых значений которых однозначно определяется одно из возможных состояний исследуемого объекта или явления;
- выражение взаимосвязей, присущих исследуемому объекту (явлению), в виде математических соотношений (уравнений, неравенств); эти соотношения образуют систему ограничений задачи;
- количественное выражение выбранного критерия оптимальности в форме целевой функции;
- математическое формулирование задачи как задачи отыскания экстремума целевой функции при условии выполнения ограничений, накладываемых па переменные [1].
Говоря о математических моделях задач линейного программирования, выделяют, как правило, несколько основных видов задач:
- задачи по определению оптимального ассортимента продукции (в качестве критериев оптимальности в них могут быть использованы прибыль, себестоимость, номенклатура производимой продукции и затраты станочного времени);
- задачи по использованию мощностей оборудования (обычно поставлены так, чтобы израсходовать все отведенное время работы машины, т.е. обеспечить полную загрузку машины, при этом количество выпускаемой продукции каждого вида должно быть, по крайней мере, не менее Nj
;
- задачи по минимизации дисбаланса на линии сборки (что по существу эквивалентно максимизации выпуска изделий);
- задачи составления кормовой смеси (задача о диете);
- задачи составления жидких смесей (класс моделей, аналогичных рассмотренным выше, возникает при решении экономической проблемы, связанной с изготовлением смесей различных жидкостей с целью получения пользующихся спросом готовых продуктов);
- задачи о раскрое или о минимизации обрезков (состоят в разработке таких технологических планов раскроя, при которых получается необходимый комплекс заготовок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму);
- транспортные задачи (по распределению ресурсов, находящихся у mпроизводителей (поставщиков), nпотребителям этих ресурсов) [3].
Обобщая их, можно сделать следующие выводы.
1. Ограничения в задачах линейного программирования могут быть выражены как равенствами, так и неравенствами.
2. Линейная функция может стремиться как к максимуму, так и к минимуму.
3. Переменные в задачах всегда неотрицательны.
Для решения задач линейного программирования в настоящее время используются несколько основных методов. Среди них:
- графический метод (используемый обычно для решения задач линейного программирования, представленных в стандартном виде, если число переменных в целевой функции и системе ограничений не более двух);
- симплексный метод (стандартный метод решения задач линейного программирования с любым числом переменных, основанный на переходе от одного опорного плана к другому, при котором значение целевой функции улучшается (по крайней мере, не ухудшается);
- решение задач линейного программирования с использованием приложения MSExcel[1].
2.2 Построение и решение ЭММ на примере ООО «Дубровчанка+»
Пользуясь статистическими данными деятельности предприятия, составим экономико-математическую модель задачи по определению оптимального ассортимента продукции.
| Наименование изделия
|
Габаритные размеры, мм
|
Ед.изм.
|
Цена, руб.
|
Усл.
обознач.
|
| Кухня "Добровчанка-Н8" (угловая, без раковины, фасад - массив, постформинг) |
2400*1600 |
к-т. |
13000-00 |
A |
| Шкаф навесной 2-х дверный (фасад - массив) |
800*320*720 |
шт. |
1300-00 |
B |
| Стол обеденный "Ладога", пластик |
110*600*750 |
шт. |
1200-00 |
C |
| Кровать подростковая 2-х ярусная |
1985*750*1650 |
шт. |
4300-00 |
F |
| Комод из массива |
800*560*850 |
шт. |
4450-00 |
G |
Для производства пяти видов продукции (в таблице) ООО «Дубровчанка +» использует древесину двух видов. Нормы затрат ресурсов на одно изделие каждого вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:
| Ресурсы |
Нормы затрат ресурсов |
Общее кол-во ресурсов |
| А |
B |
C |
F |
G |
Древесина, м3
I Вид
|
1,5
|
0,08
|
0,06
|
0,2
|
0,2
|
350
|
| IIВид |
0,2 |
0,05 |
0,04 |
0,2 |
0,1 |
130 |
| Трудоемкость, чел. - часы |
3,3 |
0,4 |
0,3 |
1 |
1,2 |
1100 |
| Прибыль от реализации, тыс. руб. |
13000 |
1300 |
1200 |
4300 |
4450 |
Определим, сколько единиц каждого изделия следует изготавливать предприятию, чтобы прибыль от их реализации была максимальной.
Решение:
Обозначим изделие каждого вида соответственно a, b, c, f, g. Тогда на изготовление всей продукции уйдет (1,5a+0,08b+0,06c+0,2f+0,2g) м3
древесины Iвида и (0,2a+0,05b+0,04c+0,2f+0,1g) м3
древесины IIвида. Так как запасы этих ресурсов не превышают 350 и 130 м3
соответственно, то
1,5a+0,08b+0,06c+0,2f+0,2g ≤ 350
0,2a+0,05b+0,04c+0,2f+0,1g ≤ 130
Трудоемкость производства этих изделий равна
(3,3a+0,4b+0,3c+1f+1,2g). Значит,
3,3a+0,4b+0,3c+1f+1,2g≤ 1100
Итак, система ограничений имеет вид:
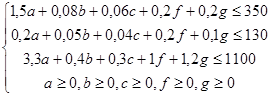
А прибыль будет выражена функцией
F=13000a+1300b+1200c+4300f+4450g
Чтобы найти решение задачи, воспользуемся MSExcel.
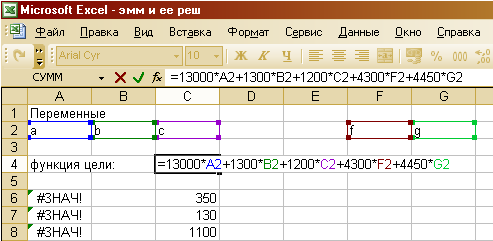
Целевую функцию зададим выражением:
=13000*A2+1300*B2+1200*C2+4300*F2+4450*G2
А систему ограничений так:
=1,5*A2+0,08*B2+0,065*C2+0,2*F2+0,2*G2
=0,2*A2+0,05*B2+0,04*C2+0,2*F2+0,1*G2
=3,3*A2+0,4*B2+0,3*C2+1*F2+1,2*G2
Открыв в меню «Сервис» команду «Поиск решения», заполним открывшееся окно: установим целевую ячейку, равную максимальному значению, определим ячейки-переменные, значения которых искомы, установим систему ограничений по имеющимся запасам сырья и располагаемой трудоемкости.
После этого в окне «Параметры» установим флажок в ячейку «Линейная модель» и выберем кнопку «Выполнить».
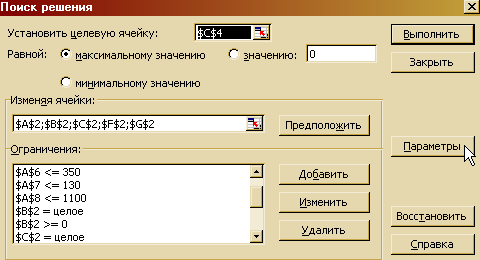
В результате решения получаем данные об оптимальном ассортименте продукции:
| Переменные |
| 160 |
0 |
20 |
429 |
114 |
| функция цели: |
4456000 |
| 349,9 |
350 |
| 130 |
130 |
| 1099,8 |
1100 |
Итак, чтобы получить максимальную прибыль 4 456 000 рублей при имеющихся запасах сырья и существующей трудоемкости получаемой продукции, предприятию следует производить 160 единиц товара вида А, 0 – вида В, 20 – вида С, 429 - вида Fи 114 – вида G.
3. ПРИМЕНЕНИЕ ТЕОРИИ ТРАНСПОРТНОЙ ЗАДАЧИ К РАБОТЕ ООО «ДУБРОВЧАНКА+»
3.1 Сущность транспортной задачи
Транспортная задача является представителем класса задач линейного программирования и поэтому обладает всеми качествами линейных оптимизационных задач, но одновременно она имеет и ряд дополнительных полезных свойств, которые позволили разработать специальные методы ее решения. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
Под термином «транспортные задачи» понимается широкий круг задач не только транспортного характера. Общим для них является, как правило, распределение ресурсов, находящихся у mпроизводителей (поставщиков), по nпотребителям этих ресурсов. Различают два типа транспортных задач: но критерию стоимости (план перевозок оптимален, если достигнут минимум затрат на его реализацию) и по критерию времени (план оптимален, если на его реализацию затрачивается минимум времени) [2].
Наиболее часто встречаются следующие задачи, относящиеся к транспортным:
- прикрепление потребителей ресурса к производителям;
- привязка пунктов отправления к пунктам назначения;
- взаимная привязка грузопотоков прямого и обратного направлений;
- отдельные задачи оптимальной загрузки промышленного оборудования;
- оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.

где n – количество пунктов отправления,
m – количество пунктов назначения,
аi
– запас продукции в пункте отправления Ai
( ) [ед. прод.], ) [ед. прод.],
bj
– спрос на продукцию в пункте назначения Bj
(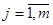 ) [ед. прод.], ) [ед. прод.],
cij
– тариф (стоимость) перевозки единицы продукции из пункта отправления Ai
в пункт назначения Bj
[руб. / ед. прод.],
xij
-
количество продукции, перевозимой из пункта отправления Ai
в пункт назначения Bj
[ед. прод.],
L(Х) – транспортные расходы на перевозку всей продукции [руб.].
Целевая функция представляет собой общие транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте.
Рассмотрим экономико-математическую модель прикрепления пунктов отправления к пунктам назначения. Имеются mпунктов отправления груза и объемы отправления по каждому пункту a1
, a2
,...,am
. Известна потребность в грузах b1
, b2
,...,bn
по каждому из
nпунктов назначения. Задана матрица стоимостей доставки по каждому варианту cij
,   . Необходимо рассчитать оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i-го пункта отправления (от поставщика) в каждый j-ый пункт назначения (до потребителя) xij
с минимальными транспортными издержками. . Необходимо рассчитать оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i-го пункта отправления (от поставщика) в каждый j-ый пункт назначения (до потребителя) xij
с минимальными транспортными издержками.
В общем виде исходные данные представлены в табл. 3.1. Строки транспортной таблицы соответствуют пунктам отправления (в последней клетке каждой строки указан объем запаса продукта ai
), а столбцы — пунктам назначения (последняя клетка каждого столбца содержит значение потребности bj
). Все клетки таблицы (кроме тех, которые расположены в нижней строке и правом столбце) содержат информацию о перевозке из i-го пункта в j-й: в правом верхнем углу находится цена перевозки единицы продукта, а в левом нижнем — значение объема перевозимого груза для данных пунктов.
Таблица 3.1
Исходные данные

Транспортная задача называется закрытой, если суммарный объем отправляемых грузов  равен суммарному объему потребности в этих грузах по пунктам назначения равен суммарному объему потребности в этих грузах по пунктам назначения  :
:
 (3.1) (3.1)
Если такого равенства нет (потребности выше запасов или наоборот), запасу называют открытой, т.е.:
 (3.2)
(3.2)
Для написания модели необходимо все условия (ограничения) и целевую функцию представить в виде математических уравнении.
Все грузы из i-х пунктов должны быть отправлены, т.е.:
 ,
, (3.3) (3.3)
Все j-е пункты (потребители) должны быть обеспечены грузами в плановом объеме:
 ,
, (3.4)
(3.4)
Суммарные объемы отправления должны равняться суммарным объемам назначения (3.1). Должно выполняться условие неотрицательности переменных:  ,
,  ,
,  . Перевозки необходимо осуществить с минимальными транспортными издержками (функция цели): . Перевозки необходимо осуществить с минимальными транспортными издержками (функция цели):
 (3.5) (3.5)
Вместо матрицы стоимостей перевозок (cij
) могут задаваться матрицы расстояний. В таком случае в качестве целевой функции рассматривается минимум суммарной транспортной работы. Как видно из выражения (3.1), уравнение баланса является обязательным условием решения транспортной задачи. Поэтому, когда в исходных условиях дана открытая задача, то ее необходимо привести к закрытой форме. В случае, если
- потребности по пунктам назначения превышают запасы пунктов отправления, то вводится фиктивный поставщик с недостающим объемом отправления;
- запасы поставщиков превышают потребности потребителей, то вводится фиктивный потребитель с необходимым объемом потребления.
Варианты, связывающие фиктивные пункты с реальными, имеют нулевые оценки. После введения фиктивных пунктов задача решается как закрытая.
Транспортным задачам присущи следующие особенности:
- распределению подлежат однородные ресурсы;
- условия задачи описываются только уравнениями;
- все переменные выражаются в одинаковых единицах измерения;
- во всех уравнениях коэффициенты при неизвестных равны единице;
- каждая неизвестная встречается только в двух уравнениях системы ограничений.
Транспортные задачи могут решаться симплекс-методом. Однако перечисленные особенности позволяют для транспортных задач применять более простые методы решения.
Опорный план является допустимым решением транспортной задачи и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов: метод северо-западного угла, метод минимального элемента и метод Фогеля. «Качество» опорных планов, полученных этими методами, различается: в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла – наихудшее.
Все существующие методы нахождения опорных планов отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода.
1. Диагональный метод, или метод северо-западного угла. При этом методе на каждом шаге построения первого опорного плана заполняется левая верхняя клетка (северо-западный угол) оставшейся части таблицы. При таком методе заполнение таблицы начинается с клетки неизвестного x11
и заканчивается в клетке неизвестного xmn
, т. е. идет как бы по диагонали таблицы перевозок.
2. Метод наименьшей стоимости. При этом методе на каждом шаге построения опорного плана первою заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф. Если такая клетка не единственная, то заполняется любая из них[2]
.
Кроме рассмотренных выше способов иногда используется, так называемый метод Фогеля. Суть его состоит в следующем: в распределительной таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится, как и ранее.
Существующий алгоритм решения транспортных задач (метод потенциалов) предполагает, что целевая функция стремится к минимуму. Однако существуют ситуации, когда в рамках транспортной модели требуется максимизировать целевую функцию, например, общий доход, объем продаж, прибыль, качество выполняемых работ и т.д.
В этом случае в модель вместо искомой целевой функции L(Х) вводится целевая функция
L1(
X)=-L(Х),
в которой тарифы умножаются на (-1). Таким образом, максимизация L(Х) будет соответствовать минимизации L1
(Х) [2]. Если в задаче идет речь о том, что из каждого пункта отправления можно перевозить продукцию нескольких видов, то при построении модели можно использовать один из следующих вариантов:
- каждому виду продукции должна соответствовать одна транспортная матрица;
- все виды продукции представлены в одной общей матрице с использованием запрещающих тарифов в клетках, связывающих разные виды продукции.
3.2 Решение транспортной задачи на примере ООО «Дубровчанка+»
Применяя теорию транспортной задачи к показателям работы ООО «Дубровчанка +», составим следующую транспортную задачу. Итак, на трех складах предприятия (назовем их С1
, С2
, С3
) сосредоточена продукция вида А в количествах 20, 14 и 38 единиц соответственно. Этот груз необходимо перевезти трем заказчикам – ООО «Пензмебкредит», ЗАО «Кузнецк-дизайн» и ТД «Столица» в количествах 44, 23, 5 единиц соответственно. Тарифы перевозок единицы груза каждого из складов потребителям задаются матрицей:
Cij
= 
Необходимо построить экономико-математическую модель задачи и составить такой план перевозок, при котором общая стоимость перевозок стала бы минимальной.
Решение:
В качестве начального этапа построения ЭММ исходный объем перевозки от i-го поставщика к j-му потребителю обозначим через аij. Заданные мощности поставщиков и спросы потребителей накладывают ограничения на значения неизвестных aij
. Так, например, объем груза, отправляемого с первого склада, должен быть равен мощности этого поставщика. Поэтому уравнения баланса имеют вид:
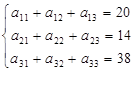
А чтобы спрос каждого из потребителей был удовлетворен, подобные уравнения баланса имеют вид:
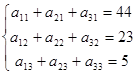
При этом суммарные затраты Fна перевозку составят:
F=143а11
+135а12
+1400а13
+104а21
+178а22
+1362а23
+102а31
+180а32
+1360а33
Для решения задачи воспользуемся пакетом MSExcelприложения MicrosoftOffice, расположив данные следующим образом (выделенные клетки – искомые значения переменных):
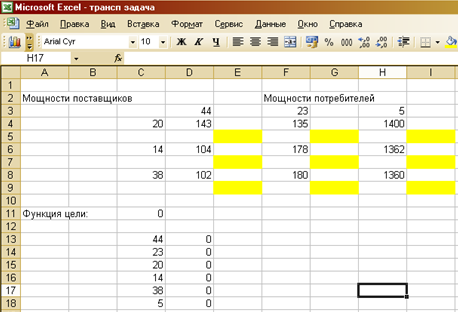
При этом целевая функция будет задана выражением:
=В4*У5+А4*П5+В6*У7+А6*П7+В8*У9+А8*П9+Р4*Ш5+Р6*Ш7+Р8*
Ш9
А система ограничений примет вид:
44=E5+E7+E9
23=G5+G7+G9
5=I5+I7+I9
20=E5+G5+I5
14=E7+G7+I7
38=E9+G9+I9
Выберем в меню «Сервис» команду «Поиск решения» и заполним открывшееся окно:

После этого в диалоговом окне «Параметры» установим флажок в ячейку «Линейная модель» и выберем кнопку «Выполнить».
В результате решения получаем оптимальный план перевозок:
 Мощности поставщиков Мощности поставщиков |
Мощности потребителей |
Запасы, к-т |
 ООО «Пензмебкредит» ООО «Пензмебкредит» |
 ЗАО «Кузнецк-дизайн» ЗАО «Кузнецк-дизайн» |
ТД «Столица» |
| С1
|
143
0
|
135
20
|
1400
0
|
20 |
| С2
|
 104 104
 14 14
|
178
 0 0
|
1362
0
|
14 |
| С3
|
102
30
|
180
3
|
1360
5
|
38 |
| Потребность, к-т |
44 |
23 |
5 |
72 |
Он означает, что с первого склада потребителю ЗАО «Кузнецк-дизайн» будет поставлено 20 единиц продукции, со второго – 14 единиц заказчику ООО «Пензмебкредит». Недопоставленные в соответствии с объемом спроса этого потребителя 30 единиц продукции будут привезены с третьего склада. Оттуда же будет поставлено 3 единицы продукции в ЗАО «Кузнецк-дизайн» и 5 единиц – в ТД «Столица». Затраты на транспортировку по данному плану составят 14 556 рублей.
ЗАКЛЮЧЕНИЕ
Необходимость решения задач линейного программирования на современных предприятиях очевидна. Построение и решение экономико-математических, а также транспортных задач позволяет, в свою очередь, решать различные технико-экономические и экономические производственные задачи, будь то проблема оптимальной загрузки станка и раскройки стального листа или анализ межотраслевого баланса и оценки темпов роста экономики страны в целом.
В данной курсовой работе были систематизированы теоретические положения по теме применения методов линейного программирования при решении экономических задач, рассмотрена сущность задач линейного программирования, выявлены основные методы решения задач линейного программирования, изучен алгоритм построения ЭММ.
Изученные теоретические положения были применены на конкретном предприятии – ООО «Дубровчанка+» в построении ЭММ по определению оптимального ассортимента продукции – был рассчитан такой план производства, при котором наблюдалась бы максимальная прибыль при располагаемом запасе ресурсов и трудоемкости технологического процесса.
Постановка и решение транспортной задачи на основе статистических данных ООО «Дубровчанка+» позволила определить оптимальный минимизирующий расходы план перевозок продукции к потребителям.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Алесинская Т.В. Учебное пособие по решению задач по курсу «Экономико-математические методы и модели». Таганрог: Изд-во ТРТУ, 2002.
2. Исследование операций в экономике. По ред. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 2010.
3. А.И. Орлов Теория принятия решений: Учебное пособие. - М.: Издательство «Март», 2004.
[1]
Основные виды изготавливаемой продукции с их габаритными размерами представлены в Таблице 1.
[2]
Замечание. В диагональном методе не учитываются величины тарифов, в методе же наименьшей стоимости эти величины учитываются, и часто последний метод приводит к плану с меньшими общими затратами, хотя это и не обязательно.
|