Министерство образования и науки Украины
Министерство образования и науки АР Крым
Малая академия наук школьников Крыма «Искатель»
Секция математики
Керченский городской филиал
Производная и ее применение для решения прикладных задач
Работу выполнил:
Коваленко Александр,
учащийся 11-Б класса
керченского учебно-воспитательного
комплекса общеобразовательной
школы
I-II ступеней- морской технический лицей
Научный руководитель:
Герасимова Валентина Леонидовна,
учитель математики,
учитель-методист
КУВК ош – МТЛ
Керчь 2008
Содержание
Введение
1. Производная и ее применение для решения прикладных задач
1.1 Исторические сведения
1.2 Понятие производной, ее геометрический и физический смысл
1.3 Дифференциал
2. Перечень прикладных задач
3. Примеры решения прикладных задач
3.1 Исследование функций и построение их графиков.
3.2 Нахождение наибольшего и наименьшего значения функции, решение прикладных задач (задач на оптимум).
3.3 Определение периода функции
3.4 Нахождение приближенных значений функции
3.5 Нахождение величины угла между прямыми и кривыми.
3.6 Разложение на множители и упрощение выражений.
3.7 Вычисление суммы
3.8 Сравнение чисел и доказательство неравенств
3.9 Решение неравенств
3.10 Доказательство тождеств
3.11. Решение уравнений
3.12 Решение систем уравнений
3.13 Отбор кратных корней уравнения
3.14 Вычисление пределов функции с помощью правила Лопиталя
3.15 Решение физических задач, связанных с нахождением скорости, ускорения и т.д.
3.16 Решение экономических задач
3.17 Разложение функций в ряд с помощью формулы Тейлора
3.18 Задача о линеаризации функции
Заключение
Список литературы
Введение
Из всех теоретических успехов знания вряд
ли какой-нибудь считается столь высоким три-
умфом человеческого духа, как изобретение ис-
числения бесконечно малых во второй половине
XVII века.
Ф. Энгельс
Тема исследовательской работы выбрана не случайно, поскольку применение производной позволяет более эффективно решать многие задачи повышенной сложности. Применение производной для решения задач требует от учащихся нетрадиционного мышления. Следует отметить, что знание нестандартных методов и приемов решения задач способствует развитию нового, нешаблонного мышления, которое можно успешно применять также и в других сферах человеческой деятельность (вычислительная техника, экономика, физика, химия и т.д.) Это доказывает актуальность данной работы.
Целью работы было: изучение применения производной для решения задач по алгебре и началам анализа, физике, экономике; углубление и расширение знаний по теме «Производная».При изучении изменяющихся величин очень часто возникает вопрос о скорости, о быстроте происходящего изменения. Так мы говорим о скорости движения самолета, поезда, автобуса, ракеты, о скорости падения камня, вращения шкива и т.д. Можно говорить о скорости выполнения определенной работы, о скорости протекания химической реакции, о быстроте роста населения в данном городе. О скорости можно говорить по отношению к любой величине, которая изменяется с течением времени. Для всего этого используется понятие производной.
Физические производные величины:
υ(t) = х/
(t) – скорость
a (t)=υ/
(t) - ускорение
J
(t) = q/
(t) - сила тока
C(t) = Q/
(t) - теплоемкость
d(l
)=m/
(l
) - линейная плотность
K (t) = l
/
(t) - коэффициент линейного расширения
ω (t)= φ/
(t) - угловая скорость
а (t)= ω/
(t) - угловое ускорение
N(t) = A/
(t) - мощность
Дифференциальное исчисление широко применяется для экономического анализа как математический аппарат. В экономике очень часто требуется найти наилучшее или оптимальное значение показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т. д. Каждый показатель представляет собой функцию от одного или нескольких аргументов. Таким образом, нахождение оптимального значения показателя сводится к нахождению экстремума функции.
Производная в экономических формулах:
П (t) = υ/
(t) - производительность труда,
где
υ (t) - объем продукции
J(x) = y/
(x) - предельные издержки производства,
где
y– издержки производства в зависимости от объема выпускаемой продукции
x.
В работе рассмотрены прикладные задачи, способы решения которых можно использовать для решения нестандартных задач по алгебре и началам анализа, при подготовке к государственной итоговой аттестации, внешнему независимому оцениванию. Достаточно большое число задач раскрывают потенциальные возможности анализа бесконечно малых величин.
1. Производная и ее применение для решения прикладных задач
1.1 Исторические сведения
Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у Евклида. Ряд таких задач был решен Архимедом, разработавшим способ проведения касательной, примененный им к спирали, но применимый для других кривых. Основное понятие дифференциального исчисления – понятие производной – возникло в XVII в. В связи с необходимостью решения ряда задач из физики, механики и математики. Дифференциальное исчисление было создано Ньютоном и Лейбницем на основе двух задач: 1) о разыскании касательной к произвольной линии2) о разыскании скорости при произвольном законе движенияЕще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда. В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.
1.2 Понятие производной, ее геометрический и физический смыслПонятие производной
Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b), и пусть х0
- произвольная точка этого промежутка
Дадим аргументу x приращение ∆x, тогда функция y = f(x) получит приращение ∆y = f(x + ∆x) - f(x). Предел, к которому стремится отношение ∆y / ∆x при ∆x → 0, называется производной от функции f(x).
y'(x)=
Геометрический смысл производной состоит в том, что она равна угловому коэффициенту касательной. Рассмотрим график функции  (рис.). Видно, (рис.). Видно,
что  , т.е. это отношение равно угловому , т.е. это отношение равно угловому
коэффициенту секущей mm. Если  , то секущая, , то секущая,
поворачиваясь вокруг точки М, в пределе переходит в
касательную  , так как касательная является предельным , так как касательная является предельным
положением секущей, когда точки пересечения сливаются.
Таким образом,  . .
Уравнение касательной
 , где , где  - координаты точки касания, а - координаты точки касания, а  - текущие координаты точки касательной прямой. - текущие координаты точки касательной прямой.
Физический смысл производной
заключается в скорости изменения функции.
Пусть s
= s
(t
) — закон прямолинейного движения. Тогда v
(t
0
) = s
'(t
0
) выражает мгновенную скорость движения в момент времени t
0
. Вторая производная a
(t
0
) = s
''(t
0
) выражает мгновенное ускорение в момент времени t
0
.Вообще производная функции y
= f
(x
) в точке x
0
выражает скорость изменения функции в точке x
0
, то есть скорость протекания процесса, описанного зависимостью y
= f
(x
).
13 Дифференциал
Пусть дана функция  и и  - внутренняя точка её области определения. Придадим аргументу приращение - внутренняя точка её области определения. Придадим аргументу приращение  и рассмотрим приращение функции и рассмотрим приращение функции
Если это приращение  можно представить в виде можно представить в виде  где величина
где величина  не зависит от приращения не зависит от приращения , а , а  - бесконечно малая при - бесконечно малая при  величина, имеющая больший порядок малости, чем величина, имеющая больший порядок малости, чем  , то произведение , то произведение  называется дифференциалом функции называется дифференциалом функции  в точке в точке  и обозначается и обозначается  . .
Перечень прикладных задач:
-составление уравнения касательной к графику функции;
-нахождение угла между пересекающимися прямыми, между графиками функций;
-исследование и построение графиков функций;
-решение задач на оптимум;
-преобразование алгебраических выражений;
-разложение многочлена на множители;
-доказательство тождеств;
-вычисление сумм;
-решение уравнений;
-приближенные вычисления и оценка погрешностей;
-доказательство неравенств и тождеств;
-решение систем уравнений;
-решение задач с параметрами;
-отбор кратных корней уравнения;
-сравнение величин;
-определение периода функции;
-нахождение пределов функции с помощью правила Лопиталя;
-разложение функций в ряд с помощью формулы Тейлора;
-приближенное решение уравнений методом проб, хорд и касательных;
-линеаризация алгебраических функций и многое другое.
3. Примеры решения прикладных задач
3.1 Исследование функций и построение их графиков
Пример 1
Исследовать и построить график функции

Решение.
1. Функция существует для всех  . .
2. Функция не является ни четной, ни нечетной,
так как
 
,
то есть  и и  . .
3. В точке х=0 функция имеет разрыв в точке х=0.
При этом  
4. Находим производную:  и приравниваем ее к нулю: и приравниваем ее к нулю:
 . Точка . Точка  будет критической. будет критической.
Проверим достаточные условия экстремума в точке  . Так как знаменатель производной всегда положителен, то достаточно проследить за знаком числителя. Получаем: . Так как знаменатель производной всегда положителен, то достаточно проследить за знаком числителя. Получаем:  при при  и и  при при  . Следовательно, в точке . Следовательно, в точке  функция имеет минимум, ее значение в точке функция имеет минимум, ее значение в точке  . .
5. Точек пересечения с осью ОY нет, так как данная функция не определена при х=0. Чтобы найти точки пересечения кривой с осью ОХ, нужно решить уравнение  . .
Тогда  или или  . .
Получим, что при  функция убывает; х= функция убывает; х= y=0; y=0;  функция убывает; при функция убывает; при  функция убывает; при х= функция убывает; при х=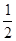 функция имеет минимум y=3; при функция имеет минимум y=3; при  функция возрастает. функция возрастает.
График данной функции представлен на рисунке.
Кривая, рассмотренная в этой задаче называется «Трезубец Ньютона».
3.2 Нахождение наибольшего и наименьшего значения функции, решение прикладных задач (задач на оптимум)
Пример 1
Из бревна, имеющего радиус R, сделать балку наибольшей прочности.
Решение:
Составляем функцию, выражающую необходимое условие.
В данной задаче высота балки (представляющей собой прямоугольник, вписанный в окружность радиуса R и ширины х), равна  . Поэтому прочность такой балки равна . Поэтому прочность такой балки равна  . При этом х изменяется от 0 до 2R. . При этом х изменяется от 0 до 2R.
Функция  обращается в нуль при х=0 и х=2R и положительна между этими значениями. Значит она имеет максимум, лежащий между 0 и 2R. Но производная этой функции обращается в нуль при х=0 и х=2R и положительна между этими значениями. Значит она имеет максимум, лежащий между 0 и 2R. Но производная этой функции  обращается в нуль на отрезке обращается в нуль на отрезке 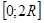 лишь при лишь при  . Это и есть оптимальное значение ширины b балки. Высота h балки такой ширины равна . Это и есть оптимальное значение ширины b балки. Высота h балки такой ширины равна  и отношение и отношение  равно равно  . Именно такое отношение высоты вытесываемой балки к ее ширине предписывается правилами производства строительных работ. . Именно такое отношение высоты вытесываемой балки к ее ширине предписывается правилами производства строительных работ.
Пример 2
Требуется построить открытый цилиндрический резервуар вместимостью  . Материал имеет толщину d. Какими должны быть размеры резервуара (радиус основания и высота), чтобы расход материала был наименьшим? . Материал имеет толщину d. Какими должны быть размеры резервуара (радиус основания и высота), чтобы расход материала был наименьшим?
Решение.
Радиус основания внутреннего цилиндра обозначим через х, высоту внутреннего цилиндра через h. Объем дна и стенки резервуара

С другой стороны, по условию  , откуда , откуда 
Подставляя в (*), находим

Полученную функцию  нужно исследовать на экстремум при х>0: нужно исследовать на экстремум при х>0:

Единственный положительный корень производной – это точка  Она и дает решение задачи. При этом Она и дает решение задачи. При этом 
3.3 Определение периода функции
Пример 1.
Является ли периодической функция  ? ?
Решение
Воспользуемся следующим утверждением: если дифференцируемая в каждой точке числовой прямой функция имеет период Т, то ее производная также имеет период Т.
Предположим, что данная функция  является периодической с периодом Т. Применяя формулу является периодической с периодом Т. Применяя формулу
 , ,
получаем
 где где  . .
Имеем

Поскольку по предположению функция  имеет период Т, то функция имеет период Т, то функция  , а следовательно, и функция , а следовательно, и функция 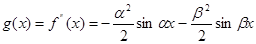 также имеют период Т. также имеют период Т.
Значит, и функция 
Также имеет период Т. Отсюда следует, что существует число  , ,  , такое, что Т= , такое, что Т= . Аналогично показывается, что существует число . Аналогично показывается, что существует число  , такое, что Т= , такое, что Т= . .
Но тогда 
т.е. число  является рациональным, что неверно. Следовательно данная функция НЕ является периодической. является рациональным, что неверно. Следовательно данная функция НЕ является периодической.
3.4 Нахождение приближенных значений функции
Пример 1.
Найти приращение и дифференциал функции в точке х=2 при  и при и при  . Найдите абсолютную и относительные погрешности, которые мы допускаем при замене приращения функции ее дифференциалом. . Найдите абсолютную и относительные погрешности, которые мы допускаем при замене приращения функции ее дифференциалом.
Решение

При х=2 и  имеем имеем

Абсолютная погрешность 
Относительная погрешность  то есть относительная погрешность будет около 4%. то есть относительная погрешность будет около 4%.
При х=2 и  имеем имеем

Абсолютная погрешность  а относительная погрешность а относительная погрешность  то есть относительная погрешность будет уже около 0,4%. то есть относительная погрешность будет уже около 0,4%.
Пример 2
Пользуясь понятием дифференциала функции вычислите приближенно изменение, претерпеваемое функцией  при изменении х от значения 5 к значению 5,01. при изменении х от значения 5 к значению 5,01.
Решение.
В данном случае будем считать х=5, а  . Изменение функции . Изменение функции

3.5 Нахождение величины угла между прямыми и кривыми.
Углом между графиками функций  и и  в точке их пересечения называется угол между касательными к их графикам в этой точке (рис.). в точке их пересечения называется угол между касательными к их графикам в этой точке (рис.).
Пример 1.
Найти угол между графиками функций  и и 
в точке их пересечения (с положительной абсциссой).
Решение.
Абсциссы точек пересечения данных графиков удовлетворяют уравнению

И тем самым следующей системе: 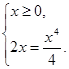
Отсюда находим, что графики функций пересекаются в двух точках, абсциссы которых равны 0 и 2. Найдем тангенсы углов наклона касательных к обоим графикам функций в точке с абсциссой, равной 2. Имеем

Отсюда  и и  Так как Так как  , то уравнения касательных к графикам функций , то уравнения касательных к графикам функций  и и  в точке (2;2) соответственно имеют вид в точке (2;2) соответственно имеют вид
 и и 
т.е.
 и и 
Следовательно величина угла  между касательными удовлетворяют уравнению между касательными удовлетворяют уравнению

и тем самым графики функций  и и  в точке с абсциссой х=2 пересекаются под углом, равным в точке с абсциссой х=2 пересекаются под углом, равным 
3.6 Разложение на множители и упрощение выражений.
Пример 1.
Разложить на множители выражение
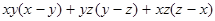 . .
Решение:
Считая х переменной величиной, рассмотрим функцию  . Имеем . Имеем  . .
Так как  , ,
то отсюда заключаем, что
 . .
Получаем  , где С не зависит от х, но зависит от y и z. , где С не зависит от х, но зависит от y и z.
Так как последнее равенство верно при любом х, то, полагая, например, в нем х=0 и учитывая, что  , найдем , найдем  . .
Таким образом,

Итак, 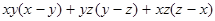 = = . .
Пример 2.
Упростить выражение

Решение
Считая х переменной величиной, рассмотрим функцию

Тогда, дифференцируя ее, имеем
 . .
Отсюда находим, что  , где С не зависит от х, но может зависеть , где С не зависит от х, но может зависеть
от y и z. Полагая, например, х=0, получаем
 . .
Поскольку  , то С=0. , то С=0.
Следовательно,  . .
3.7 Вычисление суммы
Пример 1.
Найти сумму

Решение:
Пусть  . .
Так как
 , ,
 , то , то
 . .
Поскольку  есть сумма первых есть сумма первых  членов геометрической прогрессии со знаменателем х, членов геометрической прогрессии со знаменателем х,  , то , то
 . .
Так как  , то , то
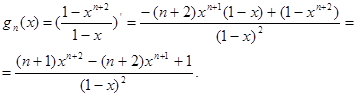

3.8 Сравнение чисел и доказательство неравенств
При доказательстве неравенств или для сравнения двух чисел полезно перейти к общему функциональному неравенству.
Пример 1.
Сравнить  и и  . .
Решение.
Рассмотрим функцию  . .
Так как
 , ,
 , ,
То функция  возрастает на интервале возрастает на интервале  . .
Таким образом,

И, следовательно,  < < . .
Пример 2.
Какое из чисел больше:  или или  ? ?
Решение.
Рассмотрим функцию  Так как Так как  и и  при при  то функция то функция 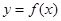 возрастает на множестве всех действительных чисел. Поэтому возрастает на множестве всех действительных чисел. Поэтому  , т.е. , т.е. 
Пример 3.
Докажите, что  при при  . .
Доказательство:
Рассмотрим функцию  при при  и и  . .
При  , ,  . .
Находим  и и  : : ; ; 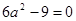 ; ;
 ; ;
  . В точке . В точке   =6, то есть =6, то есть  имеет минимум, равный имеет минимум, равный  . При . При  функция функция  убывает от убывает от  до до  , а при , а при   , то есть функция возрастает. При , то есть функция возрастает. При   , что и доказывает неравенство. , что и доказывает неравенство.
3.9 Решение неравенств
Пример 1.
 . .
Решение
Найдем участки возрастания и убывания функции  . Производная . Производная 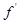 этой функции равна этой функции равна  . Так как дискриминант квадратного трехчлена . Так как дискриминант квадратного трехчлена  является отрицательным числом и коэффициент при является отрицательным числом и коэффициент при  этого квадратного трехчлена больше нуля, то для каждого действительного х имеем неравенство этого квадратного трехчлена больше нуля, то для каждого действительного х имеем неравенство  . .
Таким образом, функция 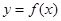 является непрерывной и возрастающей на всей числовой прямой; поэтому ее график может пересекать ось ОХ только в одной точке. Учитывая, что является непрерывной и возрастающей на всей числовой прямой; поэтому ее график может пересекать ось ОХ только в одной точке. Учитывая, что  , заключаем, что решениями данного неравенства являются все числа х из промежутка , заключаем, что решениями данного неравенства являются все числа х из промежутка  . .
Пример 2.
Докажите неравенство  (при (при  ). ).
Доказательство.
При х=0 неравенство справедливо.
Рассмотрим функцию  и найдем ее производную: и найдем ее производную:
 Производная обращается в нуль при Производная обращается в нуль при 
При  то есть функция монотонно убывает. При то есть функция монотонно убывает. При  то есть функция монотонно возрастает. При то есть функция монотонно возрастает. При 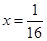 функция имеет минимум, равный нулю. функция имеет минимум, равный нулю.
Таким образом, при   значит значит  . .
Пример 3.
Доказать, что при  имеет место неравенство имеет место неравенство 
Решение.
Найдем участки возрастания и убывания функции

Так как  то то
 при при 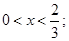
 при при 
 при при 
Функция  непрерывна на непрерывна на  поэтому она возрастает на отрезке поэтому она возрастает на отрезке  и убывает на промежутке и убывает на промежутке  Отсюда заключаем, что точка Отсюда заключаем, что точка  является точкой локального максимума функции является точкой локального максимума функции  (рис.). (рис.).
Так как  и и 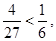 то неравенство доказано. то неравенство доказано.
3.10 Доказательство тождеств
Пример 1.

Решение
Рассмотрим функцию
 . .
При х=1 имеем  . Пусть . Пусть  ; тогда ; тогда
 и и

Поэтому  следовательно, функция следовательно, функция  при при  является тождественно равной постоянной. Чтобы найти эту постоянную, вычислим, например, является тождественно равной постоянной. Чтобы найти эту постоянную, вычислим, например,  ; имеем: ; имеем:
 . .
Таким образом, данное тождество доказано для всех  . .
3.11. Решение уравнений
Пример 1.

Решение
Переписав данное уравнение в виде
 , заметим, что его корнями являются абсциссы точек пересечения или касания графиков функций , заметим, что его корнями являются абсциссы точек пересечения или касания графиков функций  и и  . .
Для выяснения взаимного расположения графиков этих функций найдем их точки экстремумов.
Так как  , то эта функция достигает своего наименьшего значения, ровно 1, в точке х=1. Область существования функции , то эта функция достигает своего наименьшего значения, ровно 1, в точке х=1. Область существования функции  состоит из всех х таких, что состоит из всех х таких, что  . Так как . Так как

то  при при  , ,
 при при 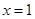 , ,
 при при  . .
Так как функция  непрерывна на непрерывна на  , то отсюда заключаем, что функция , то отсюда заключаем, что функция  возрастает на промежутке возрастает на промежутке  и убывает на промежутке и убывает на промежутке  . Следовательно, точка х=1 является наибольшим значением функции . Следовательно, точка х=1 является наибольшим значением функции  на ее области существования. на ее области существования.
Таким образом, при любом 
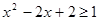 , ,
 . .
Следовательно уравнение имеет один единственный корень х=1.
Взаимное расположение графиков показано на рисунке.
3.12 Решение систем уравнений
Пример 1.
Решить систему уравнений

Решение.
Перепишем данную систему в виде

Из первого уравнения этой системы следует, что ее решениями могут быть такие пары чисел (х,y), для каждого из которых y>0. Тогда эти пары чисел должны удовлетворять неравенству х>y>0, что следует из второго уравнения системы. Пусть  тогда из первого уравнения системы находим, что тогда из первого уравнения системы находим, что  Подставляя во втором уравнении системы Подставляя во втором уравнении системы  вместо х и вместо х и  вместо y, получаем вместо y, получаем

или

Так как

то уравнение  имеет не более одного корня. Нетрудно заметить, что число t=1 является корнем. Отсюда находим, что решением данной системы может быть только пара чисел х=2 и y=1. имеет не более одного корня. Нетрудно заметить, что число t=1 является корнем. Отсюда находим, что решением данной системы может быть только пара чисел х=2 и y=1.
3.13 Отбор кратных корней уравнения
Применение производной позволяет не только убедиться в существовании кратных корней (если они есть), но и дать способ отобрать все кратные корни, отделив их от простых корней. Имеет место следующее утверждение:
Наибольший общий делитель многочленов  и и  имеет своими корнями лишь корни многочлена имеет своими корнями лишь корни многочлена  , причем только те из них, которые имеют кратность не меньше 2. Каждый их этих кратных корней многочлена , причем только те из них, которые имеют кратность не меньше 2. Каждый их этих кратных корней многочлена  является корнем наибольшего общего делителя кратности на единицу ниже. Простые корни многочлена является корнем наибольшего общего делителя кратности на единицу ниже. Простые корни многочлена  не являются корнями наибольшего общего делителя многочленов не являются корнями наибольшего общего делителя многочленов  и и  . .
Отсюда вытекает следующее правило для нахождения кратных корней уравнения:
1. Находим  . .
2. Находим наибольший общий делитель многочленов  и и  . .
3. Находим корни наибольшего общего делителя многочленов  и и  . .
Каждый из найденных корней наибольшего общего делителя многочленов  и и  является корнем многочлена является корнем многочлена  , причем кратность этого корня на единицу больше его кратности в наибольшем общем делителе. , причем кратность этого корня на единицу больше его кратности в наибольшем общем делителе.
Отметим, что если наибольший общий делитель многочленов  и и  есть константа, то уравнение есть константа, то уравнение  =0 не имеет кратных корней. =0 не имеет кратных корней.
Пример 1.
Решить уравнение
 . .
Решение.
Рассмотрим многочлен

производная которого равна

Найдем наибольший общий делитель многочленов  и и  . .
Имеем

Рис.1. - наибольший общий делитель многочленов
Таким образом, наибольший общий делитель многочленов  и и  равен х-1 (с точностью до постоянного множителя). равен х-1 (с точностью до постоянного множителя).
Так как х=1 является простым корнем наибольшего общего делителя, что число х=1 будет двукратным корнем данного уравнения, и, значит, многочлен  делится без остатка на делится без остатка на 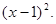 Разделив Разделив  на на  , находим, что , находим, что  Следовательно, корни исходного уравнения- это числа Следовательно, корни исходного уравнения- это числа  и х=6 и только они. и х=6 и только они.
3.14 Вычисление пределов функции с помощью правила Лопиталя
Раскрытие неопределенностей типа  и и  . Пусть однозначные функции . Пусть однозначные функции  и и  дифференцируемы при дифференцируемы при  причем производная причем производная  не обращается в нуль. не обращается в нуль.
Если  и и  - обе бесконечно малые или бесконечно большие при - обе бесконечно малые или бесконечно большие при  т.е. если частное т.е. если частное  представляет в точке х= представляет в точке х= неопределенность типа неопределенность типа  или или  , то , то  при условии, что предел отношения производных существует (правило Лопиталя). Правило применимо и в случае, когда при условии, что предел отношения производных существует (правило Лопиталя). Правило применимо и в случае, когда  . .
Если частное  вновь дает неопределенность в точке х= вновь дает неопределенность в точке х= одного из двух упомянутых типов и одного из двух упомянутых типов и  и и  удовлетворяют всем требованиям, ранее сформулированным для удовлетворяют всем требованиям, ранее сформулированным для  и и  , то можно перейти к отношению вторых производных и т.д. , то можно перейти к отношению вторых производных и т.д.
Пример 1.

Пример 2.
Вычислить  (неопределенность типа (неопределенность типа 
Приведя дроби к общему знаменателю, получим:
 (неопределенность типа (неопределенность типа 
Прежде чем применить правило Лопиталя, заменим знаменатель последней дроби эквивалентной ему бесконечно малой 
Получим:
 (неопределенность типа (неопределенность типа 
По правилу Лопиталя

Далее, элементарным путем находим:

3.15 Решение физических задач, связанных с нахождением скорости, ускорения и т.д.
Пример 1.
Дано уравнение прямолинейного движения тела:  , где S- путь, пройденный телом, м; t- время, с. Найдите скорость тела в момент времени t=1 c. , где S- путь, пройденный телом, м; t- время, с. Найдите скорость тела в момент времени t=1 c.
Решение.
Скорость это производная пути по времени. Значит: 
Подставив значение времени получим: 
Пример 2.
Точка движется по закону  . Найти скорость и ускорение через 2 с после начала движения (движение считать прямолинейным). . Найти скорость и ускорение через 2 с после начала движения (движение считать прямолинейным).
Решение.
Скорость это производная пути по времени. Значит:  . .
Подставив значение времени получим 
Пример 3.
Тело движется прямолинейно по закону  Найти его кинетическую энергию через 5 с после начала движения, если масса тела 3 кг. Найти его кинетическую энергию через 5 с после начала движения, если масса тела 3 кг.
Решение.
Формула нахождения кинетической энергии:  . .
Найдем скорость тела. 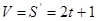 , ,  . .
Кинетическая энергия тела составит:  . .
3.16 Решение экономических задач
Пример 1.
Выбрать оптимальный объем производства фирмой, функция прибыли которой может быть смоделирована зависимостью:
π(q) = R(q) - C(q) = q2
- 8q + 10
Решение:
π'(q) = R'(q) - C'(q) = 2q - 8 = 0 → qextr
= 4
При q < qextr
= 4 → π'(q) < 0 и прибыль убывает
При q > qextr
= 4 → π'(q) > 0 и прибыль возрастает
При q = 4 прибыль принимает минимальное значение.
Каким же будет оптимальный объем выпуска для фирмы? Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (p(q = 8) = p(q = 0) = 10), то оптимальным решением будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и / или оборудования. Если же фирма способна производить больше 8 единиц, то оптимальным для фирмы будет выпуск на пределе своих производственных мощностей.
Пример 2.
Кривая спроса задана выражением  , где , где  - объем продаж; - объем продаж;  - цена товара в условных единицах. Объем продаж составляет 10 000. Определите, каким должно быть изменение цены товара, чтобы объем продаж возрос на 1%. - цена товара в условных единицах. Объем продаж составляет 10 000. Определите, каким должно быть изменение цены товара, чтобы объем продаж возрос на 1%.
Решение.
Определим цену  , соответствующую объему продаж , соответствующую объему продаж 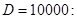

Для оценки изменения цены товара воспользуемся формулой приближенных вычислений  По условию задачи По условию задачи  составляет 1% от 10000 или 10000/100=100. Найдем значение составляет 1% от 10000 или 10000/100=100. Найдем значение 

Тогда  Таким образом, для увеличения объема продаж на 1% цена товара должна быть снижена приблизительно на 0,105 у.е. Таким образом, для увеличения объема продаж на 1% цена товара должна быть снижена приблизительно на 0,105 у.е.
3.17 Разложение функций в ряд с помощью формулы Тейлора
1) Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.(Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности).
2) Пусть х- любое значение из этой окрестности, но х а.
Тогда между точками х и а найдется такая точка , что справедлива формула:

- это выражение называется формулой Тейлора, а выражение:

называется остаточным членом в форме Лагранжа.
При  получаем формулу Маклорена: получаем формулу Маклорена:

где  , , 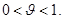
Пример 1.
Многочлен  разложить по целым положительным степеням бинома х-2. разложить по целым положительным степеням бинома х-2.
Решение.

Отсюда: 
Следовательно,  или или

Пример 2.
Функцию  разложить по степени бинома х+1 до члена, содержащего разложить по степени бинома х+1 до члена, содержащего 
Решение
 для всех n, для всех n,  Следовательно , Следовательно ,
 где где 
Пример 3
Разложить функцию  в ряд Маклорена. в ряд Маклорена.
Решение.
Как известно, этот интеграл нельзя выразить через элементарные функции. Для отыскания разложения данного интеграла в ряд Маклорена необходимо разложить подынтегральную функцию в степенной ряд, а затем почленно проинтегрировать (степенной ряд сходится равномерно на любом отрезке, лежащем внутри промежутка сходимости, поэтому его можно проинтегрировать почленно).
3.18 Задача о линеаризации функции
По всей вероятности, исторически задача стояла так: «Написать уравнение касательной к графику функции 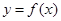 в точке с абсциссой в точке с абсциссой  ». Дело в том, что ученым (в частности вычислителям) надо было в случае довольно «громоздкой» зависимости между переменными заменить в окрестности некоторой точки эту зависимость более простой. А самой простой является линейная зависимость. Поэтому вместо сформулированной выше задачи выдвинулись требования: «Заменить данную функцию линейной функцией в окрестности точки ». Дело в том, что ученым (в частности вычислителям) надо было в случае довольно «громоздкой» зависимости между переменными заменить в окрестности некоторой точки эту зависимость более простой. А самой простой является линейная зависимость. Поэтому вместо сформулированной выше задачи выдвинулись требования: «Заменить данную функцию линейной функцией в окрестности точки  ». Эта идея занимала Тейлора. В случае, если эта замена давала вычислителям большие погрешности, ставилась задача замены данной функции в окрестности точки ». Эта идея занимала Тейлора. В случае, если эта замена давала вычислителям большие погрешности, ставилась задача замены данной функции в окрестности точки  квадратичной функцией, многочленом третьей степени, четвертой и т.д.- до тех пор, пока не получалась нужная точность вычислений. Эта идея имеет простой геометрический смысл: при замене данной функции линейной в окрестности точки квадратичной функцией, многочленом третьей степени, четвертой и т.д.- до тех пор, пока не получалась нужная точность вычислений. Эта идея имеет простой геометрический смысл: при замене данной функции линейной в окрестности точки  рассматривается касательная рассматривается касательная  , при замене квадратичной- соприкасающаяся парабола, при замене многочленом третьей степени- соприкасающаяся кубическая парабола и т.д. , при замене квадратичной- соприкасающаяся парабола, при замене многочленом третьей степени- соприкасающаяся кубическая парабола и т.д.
Замена данной функции линейной получила название линеаризации. Поскольку не было явно сформулировано понятие предела (это уже IX век), то на основе интуиции бесконечно малые «более высоких порядков» просто отбрасывались.
Пример 1.
Замените данную функцию линейной вблизи нуля:

Решение.
Если  , то , то  так же стремятся к нулю, поэтому ими можно пренебречь, то есть отбросить. В результате получаем так же стремятся к нулю, поэтому ими можно пренебречь, то есть отбросить. В результате получаем 
Пример 2.
Замените данную функцию линейной вблизи нуля:

Решение.
Отбрасываем в числителе и знаменателе х в степени выше первой: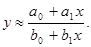
Умножим числитель и знаменатель дроби на двучлен, сопряженный со знаменателем:

Отбрасываем в числителе и знаменателе х в степени выше первой. Будем иметь
 или или 
Заключение
В ходе написания работы были использованы такие ключевые понятия дифференциального исчисления как производная, дифференциал, геометрический и физический смысл производной, касательная к графику функции и многое другое, которые используются для решения прикладных задач в математике, физике, экономике.
Цель данной работы - которые решаются с помощью производной.
Список использованной литературы:
1. Терешин Н.А., Терешина Т.Н. «2000 задач по алгебре и началам анализа. 10 кл./
-М.:Аквариум, К.: ГИППВ, 2000. 256 с. Стр.192-193; 216-217; 194; 200; 240.
2. Ф.Ф.Нагибин «Экстремумы»/- М. «Просвещение» 1966 г. Стр. 30-35.
3. Виленкин Н.Я. «Функция в природе и технике»: Кн. для внеклас. чтения IX-X кл. – 2-е изд., испр. –М.: Просвещение, 1985. – 192 с. Стр.88; 94.
4. О.Н. Афанасьева «Сборник задач по математике для техникумов» - М.:Наука 1992.-208 с. Стр.84.
5. Н.В. Мирошин «Сборник задач с решениями для поступающих в вузы.» - М.: ООО «Издательство Астрель» 2002.-832 с. Стр.496.
6. Вавилов В.В. «Задачи по математике. Начала анализа.»-М.: Наука.Гл. ред.физ.-мат.лит., 1990.-608 с. Стр. 411;412-413; 413-414; 416-417; 419-420; 432-433; 422; 423; 424; 430; 365.
7. Мышкис А.Д. «Лекции по высшей математике» Изд. «Наука» 1967 г. Стр. 135.
8. Глейзер Г.И. «История математики в школе» - М.: Просвещение, 1983 г. Стр. 42.
9. Волькенштейн В.С. «Сборник задач по общему курсу физики» М., 1979 г.
10. «Математический энциклопедический словарь.»/Гл.ред. Ю.В.Прохоров.-М:Сов.энциклопедия, 1988.-847 с.
11. «Задачник по курсу математического анализа». ч.II. Под ред. Н.Я.Виленкина.-М: «Просвещение», 1971.
12. «Задачи и упражнения по математическому анализу для втузов.»/Под ред. Б.П.Демидовича- М: Физматгиз, 1963 г. 472 стр.
13. «Элементы высшей математики»: сб. заданий для практ. занятий: Учеб. Пособие/ С.В.Сочнев.-М: Высш.шк., 2003 г.- 192 с.
|