ПРОСТОЕ ДОКАЗАТЕЛЬСТВО
ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА
Файл: FERMA-UVar
© Н.М. Козий, 2007
Авторские права защищены свидетельствами Украины
№ 22108 и № 27312
Великая теорема Ферма формулируется следующим образом: диофантово уравнение (http: // soluvel. okis. ru/evrika. html):
Аn+ Вn = Сn/1/
где n - целое положительное число, большее двух, не имеет решения в целых положительных числах.
Суть Великой теоремы Ферма не изменится, если уравнение /1/ запишем следующим образом:
Аn = Сn - Вn/2/
Уравнение /2/ рассматриваем как параметрическое уравнение n - ной степени с параметром A и переменными Bи С.
Уравнение /2/ запишем в следующем виде:
Аn = (С0,5n) 2 -(В0,5n) 2 /3/
Обозначим:
В0,5n =V/4/
С0,5n =U/5/
Отсюда:
Вn=V2 /6/
Сn =U2 /7/
В = /8/ /8/
С =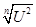 /9/ /9/
Тогда из уравнений /2/, /6/ и /7/ следует:
Аn = Сn - Вn =U2-V2/10/
Уравнение /10/ в соответствии с известной зависимостью для разности квадратов двух чисел запишем в виде:
Аn=(U-V) ∙(U+V) /11/
Для доказательства великой теоремы Ферма используем метод замены переменных. Обозначим:
U-V=X/12/
Из уравнения /12/ имеем:
U=V+X/13/
Из уравнений /11/, /12/ и /13/ имеем:
Аn=X∙ (V+X+V) =X∙(2V+X) = 2VX+X2 /14/
Из уравнения /14/ имеем:
Аn - X2=2VХ /15/
Отсюда:
V=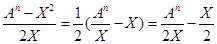 /16/ /16/
Из уравнений /13/ и /16/ имеем:
U=  /17/ /17/
Из уравнений /8/, /9/, /16/ и /17/ имеем:
В=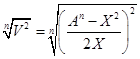 /18/ /18/
C = /19/ /19/
Из уравнений / 18/ и /19/ следует, что необходимым условием для того чтобы числа В и С были целыми, является делимость числа А на число X, т.е. число Xдолжно быть одним из множителей, входящих в состав множителей числа А. Другими словами, число А должно быть равно:
A = N∙ X, /20/
где N - простое или составное целое положительное число.
Из уравнений / 18/ и /19/ следует, что необходимым условием для того чтобы числа В и С были целыми, является также одинаковая четность чисел Aи X: оба числа должны быть четными или оба нечетными.
Из уравнений / 18/, /19/ и /20/ следует:
В= /21/ /21/
C= /22/ /22/
Обозначим:
P =  /23/ /23/
Q =  /24/ /24/
Тогда:
B =  /25/ /25/
С = /26/ /26/
Из уравнений /23/ и /24/ имеем:
Q = 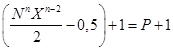 /27/ /27/
Таким образом, из уравнений /26/ и /27/ следует:
С =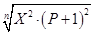 /28/ /28/
Из анализа уравнений /25/ и /28/ следует. Что поскольку разность между числами Pи Qравна всего лишь:
Q- P = P + 1 - P = 1,
то по меньшей мере одно из чисел В или С является дробным числом.
Если допустить, что число В - целое число, например равно:
B = 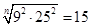 , то: , то:
С =  - дробное число. - дробное число.
Таким образом, одно из чисел В или С - дробное число.
Следовательно, великая теорема Ферма не имеет решения в целых положительных числах.
В частном случае, если показатель степени n =2, из формул /18/ и/19/ имеем:
 B=V= B=V= ; C=U= ; C=U=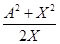 . /29/ . /29/
При условии, что числа Aи Xимеют одинаковую четность и число Xявляется делителем числа A, по формулам /22/ определяются пифагоровы числа Bи Cдля числа A.
|