Министерство образования и науки Российской Федерации
Филиал ГОУ ВПО « Сочинский государственный университет
туризма и курортного дела» в г. Омске Омской области
кафедра менеджмента
СТАТИСТИКА
ПИСЬМЕННАЯ КОНСУЛЬТАЦИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению контрольных работ для студентов заочной и очно-заочной форм обучения
Старший преподаватель: БЕЛОЗЕРОВА Е. А.
2010г.
СОДЕРЖАНИЕ
1.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ И СХЕМЫ РЕШЕНИЙ ПРАКТИЧЕСКИХ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ №1 ПО РАЗДЕЛУ «ТЕОРИЯ СТАТИСТИКИ» КУРСА «СТАТИСТИКА»
3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ И СХЕМЫ РЕШЕНИЙ ПРАКТИЧЕСКИХ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ №2 ПО РАЗДЕЛУ «СТАТИСТИКА ПРЕДПРИЯТИЯ» КУРСА «СТАТИСТИКА»
4. ЛИТЕРАТУРА И УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данная консультация предлагается в помощь студентам 2 курса заочной и очно-заочной форм обучения. В ней представлены методические указания и схемы решений практических заданий контрольной работы № 1 по разделу «Теория статистики» курса «Статистика» и контрольной работы № 2 по разделу «Статистика предприятия» курса «Статистика».
Студенты выполняют контрольную работу по одному из двух рекомендованных вариантов.
Варианты с заданиями контрольных работ представлены в пособии «Статистика: Методические указания по выполнению контрольных работ / Сост. Е, А. Белозерова – Омск: ФСГУТ и КД в г. Омске, 2004. -37с.» и выдаются в библиотеке филиала.
Каждый вариант контрольной работы № 1 включает теоретический вопрос и восемь практических задач. Каждый вариант контрольной работы № 2 предусматривает обязательное выполнение трех из восьми практических заданий (№2, №3, №4).
Приступая к решению конкретной задачи, необходимо понять ее условия и требования. При решении задач нельзя ограничиваться записью одних ответов на задачи. Надо показать в контрольной работе ход решения каждой задачи, применение тех или иных формул, по полученным результатам сделать выводы. Расчеты показателей, таблицы, их наименование и единицы измерения, а также соответствующие выводы, предусмотренные задачами, следует составлять четко и точно.
При составлении таблиц следует руководствоваться правилами и требованиями к составлению статистических таблиц, приведенными в учебниках по курсу «Теория статистики».
Средние, относительные величины в процентах должны исчисляться с точностью до одной сотой; индексы, доли единицы и коэффициенты – с точностью до одной тысячной.
Контрольную работу следует выполнять грамотно, аккуратно, без сокращения слов, оставляя поля и свободное место для возможных замечаний и рецензий преподавателя. В конце работы необходимо указать перечень использованной литературы и учебных пособий, дату выполнения и свою подпись.
Требования к оформлению.
Выполненные задания располагаются по представленному порядку. В конце работы необходимо указать перечень использованной литературы и учебных пособий, дату выполнения и свою подпись. На титульном листе располагается следующая информация: название дисциплины, Ф.И.О. студента, курс, группа, номер контрольной работы, номер выбранного варианта и номера выполненных заданий по порядку в следующем виде:
Контрольная работа по статистике №
Вариант №
|
| Задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| Оценка |
Сроки выполнения.
Выполненная контрольная работа подписывается студентом и сдается на проверку преподавателю на кафедру менеджмента в установленные сроки, как правило, за 10дней до начала сессии. Проверка контрольной работы преподавателем осуществляется в течение недели после ее сдачи. Контрольная работа должна быть зачтена к началу экзаменационной сессии.
Критерии оценки контрольной работы.
При соответствии контрольной работы требованиям методических указаний, правильных и полных ответов на вопросы, верно решенных задачах, преподаватель ставит на титульном листе «Зачтено» и подпись. Если в результате проверки обнаружены существенные ошибки, неполный объем или низкое качество оформления работы, она возвращается студенту для доработки или переделки. Замечания преподавателя в письменном виде на полях работы и на титульном листе представляются студенту. На титульном листе ставится «Доработать» или «Переделать» и подпись. После доработки или переделки контрольная работа повторно сдается на проверку преподавателю. По результатам повторной проверки студент защищает исправленную работу – поясняет работу над ошибками, отвечает на возникающие у преподавателя вопросы по существу выполняемых заданий.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И СХЕМЫ РЕШЕНИЙ ПРАКТИЧЕСКИХ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ №1 ПО РАЗДЕЛУ «ТЕОРИЯ СТАТИСТИКИ» КУРСА «СТАТИСТИКА»
ЗАДАЧА 1
Имеются следующие данные о проценте выполнения норм выработки тридцатью рабочими ремонтной бригады:
Выполнение норм выработки рабочими (%):
96 95 98 98 112 115 114 106 102 111
100 95 110 102 104 106 101 112 97 107
105 104 103 102 107 108 102 108 106 103
Требуется построить интервальный вариационный ряд распределения рабочих по нормам выработки, выделив 4 группы с равными интервалами. Сделайте выводы.
РЕШЕНИЕ:
(См. учебное пособие В. М. Гусарова «Статистика», М.: ЮНИТИ - ДАНА, 2003, с.39-45).
1) Группировочный признак – норма выработки, минимальное значение выполнения нормы выработки рабочими (XMIN
) – 95%, максимальное значение (XMAX
) – 115%, число групп дано в условии n = 4, отсюда определим величину равновеликого интервала (i):
=(XMAX
- XMIN
): 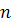 ; ; 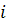 =(115-95):4=5% =(115-95):4=5%
2) Зная величину интервала, определим границы групп по нормам выработки рабочих (в %). Нижней границей первой группы является минимальное значение признака в совокупности XMIN
=95%, верхняя граница получается путем прибавления величины интервала 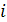 =5% к нижней границе. Нижней границей следующей группы служит верхняя граница предыдущей группы, а верхняя граница данной группы больше ее нижней границы на величину интервала: =5% к нижней границе. Нижней границей следующей группы служит верхняя граница предыдущей группы, а верхняя граница данной группы больше ее нижней границы на величину интервала:
1 группа – от 95 до 100 (XMIN
+ 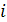 ; 95%+5%) ; 95%+5%)
2 группа – от 100 до 105 (100% +5%)
3 группа – от 105 до 110 (105%+5%)
4 группа – от 110 до 115 (110%+5%)
3) В таблице 1 построим ряд распределения рабочих по нормам выработки путем подсчета частот
(
fi
)
- абсолютного значения числа рабочих в каждой группе. В графе 1 указываются по порядку варианты (
xi
)
- значения признака в границах группы (нормы выработки), а в графе 2 – абсолютное число единиц (рабочих), входящих в данный интервал (частоты fi
):
Таблица 1
Распределение рабочих ремонтной бригады по выполнению норм выработки
Группы рабочих по выполнению норм выработки, %
(варианты xi
)
|
Число рабочих, чел
(частотыfi
)
|
Структура рабочих по нормам выработки
(частости wi
= fi
/∑fi
)
|
Сумма накопленных частот,
(кумулятивные частоты Si
)
|
| в долях единицы |
Удельный вес в % к итогу |
| 1 |
2 |
3 |
4 |
5 |
95-100
100-105
105-110
110-115
Итого
|
7
10
8
5
30
|
0,233
0,333
0,267
0,167
1,000
|
23,3
33,3
26,7
16,7
100,0
|
7
17 (7+10)
25 (17+8)
30 (25+5)
-
|
4) Определим структуру распределения рабочих бригады по выполнению норм выработки. Структура распределения выражается относительными величинами (частостями)
и определяется в долях единицы (графа 3) или в процентах (графа 4). Частость или число рабочих в долях единицы определяется делением частоты соответствующей группы на сумму частот: wi
= fi
/ ∑fi
, частость в процентах или удельный вес группы в общей численности совокупности определяется умножением соответствующей доли на 100%. Так, доля рабочих в общей численности рабочих бригады:
в первой группе w1
= f1
/ ∑fi
= 7:30=0,233 или удельный вес рабочих первой группы в общей численности рабочих бригады составил 23,3%;
во второй группе w2
= f2
/ ∑fi
=10:30=0,333 или 33,3% и т. д.Сумма долей равна 1, сумма удельных весов равна 100%.
5) Кроме обычных частот в вариационном ряду рассчитывают нарастающим итогом накопленные (кумулятивные) частоты
, по которым строят суждение о том, какое число единиц в совокупности обладает значением признака «не более» или «не менее» определенного. Рассчитаем кумулятивные частоты (графа 5) путем последовательного суммирования частот ряда: S1
= 7; S2
= 7+10 = 17; S3
= 17+8 = 25; S4
= 25+5 = 30.
ВЫВОД.
По данным ряда распределения можно сделать вывод о характере распределения рабочих по выполнению норм выработки и их структуре:
1) наибольшее число рабочих – 10 человек или 33,3% от общего числа выполняют норму выработки от 100 до 105%,
2) затем по численности следует группа из 8 человек (26,7% от общего числа), которые выполняют норму выработки от 105 до 110%.
Кумулятивные частоты распределения показывают, что:
1) из всей численности рабочих ремонтной бригады норму выработки, не превышающую 100%, выполняют 7 человек или 23,3% рабочих бригады;
2) у 17 человек (56,6% от численности бригады) норма выработки не превышает 105%;
3) у 25 рабочих (83,3% от численности рабочих бригады) норма выработки не превышает 110%;
4) 5 рабочих, составляющих 16,7% от общей численности бригады выполняют норму выработки от 110 до 115%.
Таким образом, в ремонтной бригаде норму выработки перевыполняют 23 человека, что составляет 76,7% от числа рабочих в бригаде.
ЗАДАЧА 2
Имеются следующие данные о выпуске трех видов продукции предприятием за 2008-2009гг.:
| Вид продукции |
Выпуск продукции в 2009г., тыс. руб. |
Выполнение бизнес-плана в 2009г., % |
Выпуск продукции в 2008г., тыс. руб. |
| бизнес-план |
факт |
| 1 |
2 |
3 |
4 |
5 |
| А |
2850 |
102,5 |
2710 |
| Б |
2720 |
98,3 |
2560 |
| В |
3350 |
3420 |
3100 |
| Всего |
Определите: 1.Недостающие показатели в таблице.
2.Фактическую структуру продукции за 2008г. и 2009г.
3.Относительные величины динамики производства продукции в 2009 году по сравнению с 2008 годом (по плану и фактически).
По исходным и полученным данным постройте аналитическую таблицу, укажите виды относительных величин и сформулируйте выводы.
РЕШЕНИЕ
(представим в аналитической таблице 2)
( См. учебное пособие В. М. Гусарова «Статистика», М.: ЮНИТИ - ДАНА, 2003, с.39-45).
1) Определим недостающие в таблице показатели:
а) Фактическое производство
продукции А в 2009г. (Ф1
) найдем из формулы:
ОВВП = (Ф1
/П1
)×100% (1),
где ОВВП – относительная величина выполнения плана
Ф1
– фактический уровень показателя в отчетном периоде
П1
– запланированный уровень показателя в отчетном периоде
Следовательно, недостающий показатель фактического производства
продукции А в 2009г.:
Ф1
= (П1
×ОВВП)/100%, Ф1
= (2850×102,5)/100% = 2921,25 тыс.руб.
б) Запланированный уровень производства
продукции Б в 2009г. (П1
) также найдем из формулы (1):
П1
= (Ф1
/ОВВП)×100%, П1
= (2720×100%)/98,3 = 2767,04 тыс.руб.
Таблица 2
Оценка изменения выпуска продукции предприятием за 2008-2009г.
| Вид проду кции |
Выпуск продукции в 2009г., тыс.руб. |
Выпол нение бизнес-плана в 2009г., %
(ОВВП)
|
Выпуск продук ции в 2008г., тыс.руб.
(Ф0
)
|
Удельный вес продукции по факту,% к итогу |
Темпы роста 2009г. к 2008г., % |
| бизнес-план (П1
) |
Факт
(Ф1
)
|
| 2008г. |
2009г. |
по плану |
по факту |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| А |
2850,0
|
2921,2 |
102,5
|
2710,0
|
32,4 |
32,2 |
105,2 |
107,8 |
| Б |
2767,0 |
2720,0
|
98,3
|
2560,0
|
30,6 |
30,0 |
108,1 |
106,3 |
| В |
3350,0
|
3420,0
|
102,1 |
3100,0
|
37,0 |
37,8 |
108,1 |
110,3 |
| Всего |
8967,0 |
9061,2 |
101,1 |
8370,0 |
100,0 |
100,0 |
107,1 |
108,3 |
в) Степень выполнения бизнес-плана
выпуска продукцииВ (графа4)определим по формуле (1):
ОВВП = (3420/3350)×100% = 102,1%
г) Общий объем производства продукции за 2009г.
(итоговая строка) составил: по плану Σ П1
= 2850 + 2767,04 + 3350 = 8967,04 тыс.руб.
по факту Σ Ф1
= 2921,25 + 2720 + 3420 = 9061,25 тыс.руб.
Степень выполнения плана
по всем видам продукции за 2009г. (итоговая строка графы 4) составляет:
ОВВП = (ΣФ1
/ΣП1
)×100% = (9061,25/8967,04)×100% = 101,1%
д) Фактическое производство
по всем видам продукции за 2008г. (итоговая строка графы5):
ΣФ0
= 2710 + 2560 +3100 = 8370 тыс.руб.
где Ф0
– фактическое производство в базисном периоде, которым является 2008г. по отношению к отчетному 2009г.
2) Определим фактическую структуру
продукции по формуле:
ОВС = (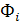 / Σ / Σ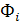 )×100% (2), )×100% (2),
статистика таблица контрольная работа
где ОВС – относительная величина структуры (удельный вес части в целом)
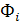 – абсолютная величина части целого (производство отдельных видов продукции) – абсолютная величина части целого (производство отдельных видов продукции)
Σ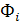 – абсолютная сумма частей целого (общий выпуск продукции) – абсолютная сумма частей целого (общий выпуск продукции)
а) За 2008г. (графа 6 по графе 5) удельный вес отдельных видов продукции в общем объеме выпуска по формуле (2
)составил:
Уд. вес продукции А = (2710/8370)×100% = 32,4%
Уд. вес продукции Б = (2560/8370)×100% = 30,6%
Уд. вес продукции В= (3100/8370)×100% = 37,0%
Итого: 100,0%
б) За 2009г. (графа 7 по графе 3) удельный вес отдельных видов продукции в общем объеме выпуска по формуле (2)
составил:
Уд. вес продукции А = (2921,25/9061,25)×100% = 32,2%
Уд. вес продукции Б = (2720/9061,25)×100% = 30%
Уд. вес продукции В = (3420/9061,25)×100% = 37,8%
Итого: 100,0%
3) Определим относительные величины плановой и фактической динамики
.
а) Относительная величина плановой динамики или планового задания (ОВПЗ) –
это темп роста по плану (графа 8), определяется как отношение запланированного уровня на отчетный период (П1
) к фактическому уровню базисного периода (Ф0
):
ОВПЗ= (П1
/Ф0
)×100% (3)
В 2009 г. по сравнению с 2008г. запланированные темпы роста выпуска отдельных видов продукции по формуле (3)
составили:
для продукции А ОВПЗА
= (2850/2710)×100% = 105,2%
для продукции Б ОВПЗБ
= (2767,04/2560)×100% = 108,1%
для продукции В ОВПЗВ
= (3350/3100)×100% = 108,1%
для всех видов продукции ОВПЗ2009
= (8967,04/8370)×100% = 107,1%
б) Темп фактического роста (Тр
) или относительная величина динамики (ОВД)
– это соотношение фактических уровней одного и того же показателя в отчетном и базисном периодах (графа 9), определяется по формуле:
Тр = (Ф1
/Ф0
)×100% (4)
Фактические темпы роста выпуска продукции в 2009г. по сравнению с 2008г.по формуле (4) составили:
продукции А: Тр
= (2921,25/2710)×100% = 107,8%
продукции Б: Тр
= (2720/2560)×100% = 106,3%
продукции В: Тр
= (3420/3100)×100% = 110,3%
всех видов продукции: Тр
= (9061,25/8370)×100% = 108,3%
Выводы:
1. План выпуска всех видов продукции в целом на предприятии в 2009 году перевыполнен на 1,1%, в том числе по продукции А на 2,5%, по продукции В на 2,1%, а по продукции Б план выпуска не выполнен на 1,7% ( по графе 4).
2. В 2009 г. по сравнению с 2008г. планировался рост общего объема выпуска продукции на 7,1%, в том числе рост выпуска продукции А - на 5,2%, продукции Б - на 8,1%, продукции В также на 8,1% (по графе 8).
3. Фактически выпуск продукции в 2009 году по сравнению с 2008 годом увеличился на 8,3%, в том числе продукции А - на 7,8%, продукции Б - на 6,3%,продукции В - на 10,3% (по графе 9).
4. Удельный вес в общем объеме выпуска продукции за 2008г. составил: продукции А -32,4%, продукции Б – 30,6%, продукции В – 37,0% (по графе 6).Существенных структурных сдвигов в выпуске продукции на предприятии в 2009г. по сравнению с 2008г. не наблюдалось, так удельный вес продукции А в общем объеме выпуска в 2009г. составил 32,2% (было 32,4%), продукции Б – 30,0% (было 30,6%), продукции В – 37,8% (было37,0%).
ЗАДАЧА 3
Имеются следующие данные о стоимости продукции и ее выработке рабочими в разных бригадах (таблица 3):
Таблица 3
Стоимость и выработка продукции рабочими в разных бригадах
| Номер бригады |
Стоимость произведенной продукции, тыс.руб.
(М = х ×
f
)
|
Число рабочих, чел.
(
f
)
|
Выработка
на одного рабочего,
тыс. руб.
(х)
|
| А |
1 |
2 |
3 |
1
2
3
|
460
650
700
|
23
26
25
|
20
25
28
|
| Итого (∑) |
1810 |
74 |
- |
На основе приведенных данных определите среднюю выработку на одного рабочего в целом по трем бригадам, используя данные:
А) граф 1 и 2;
Б) граф 1 и 3;
В) граф 2 и 3.
Укажите виды средних и сделайте выводы.
РЕШЕНИЕ:
(См. учебное пособие В. М. Гусарова «Статистика», М.: ЮНИТИ - ДАНА, 2003, с.56-66).
1) В зависимости от исходных данных среднее значение того или иного признака может рассчитываться по-разному. Чтобы установить формулу расчета для конкретного варианта данных, необходимо определить исходное соотношение средней
для осредняемого признака, в нашем примере этим признаком является показатель «средняя выработка». Независимо от исходных данных, средняя выработка одного рабочего может быть получена через следующее соотношение:
_ Стоимость произведенной продукции (М)
Средняя выработка (х
)= ______________________________________
Численность рабочих (
f
)
2) По данным граф 1 и 2 известны и числитель (М), и знаменатель (f) логической формулы, следовательно, нужна формула средней агрегатной:
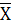 = ΣМ / Σ
f
; = ΣМ / Σ
f
;
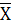 = (460+650+700)/(23+26+25) = 1810/74 = 24,5 (тыс.руб.) = (460+650+700)/(23+26+25) = 1810/74 = 24,5 (тыс.руб.)
3) По данным граф 1 и 3 известен только числитель (М) логической формулы и неизвестен знаменатель (f), но даны отдельные варианты (х), следовательно, применим среднюю гармоническую взвешенную:
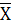 = ΣМ / Σ(М / х); = ΣМ / Σ(М / х);
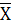 =(460+650+700)/(460/20+650/25+700/28)=1810/74 = 24,5 (тыс. руб.) =(460+650+700)/(460/20+650/25+700/28)=1810/74 = 24,5 (тыс. руб.)
4) По данным граф 2 и 3 известен знаменатель логической формулы (f) и отдельные варианты (х), но неизвестен числитель логической формулы (М), следовательно, применим среднюю арифметическую взвешенную:
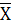 = Σх
f
/ Σ
f
; = Σх
f
/ Σ
f
;
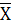 =(20×23+25×26+28×25)/(23+26+25)= 1810/74 =24,5 (тыс.руб.) =(20×23+25×26+28×25)/(23+26+25)= 1810/74 =24,5 (тыс.руб.)
Вывод.
Средняя выработка на одного рабочего по трем бригадам составила 24,5 тыс. руб. Для определения средней выработки на одного рабочего по разным вариантам исходных данных использовались разные формулы средних, но получился один и тот же ответ - 24,5 тыс. руб., так как для разных условий данных каждый раз реализовывалось одно и то же исходное соотношение средней. Это объясняется тем, что на базе научного статистического метода расчета средних величин, для каждого конкретного показателя, используемого в социально-экономических расчетах, можно исчислить только одно истинное значение средней.
ЗАДАЧА 4
Для оценки выпуска продукции предприятиями области проведена 10%-ная механическая выборка, в результате чего установлено (таблица 4):
Таблица 4
Распределение предприятий области по выпуску продукции
Группы предприятий по выпуску продукции,
млн. руб.
|
Число предприятий |
| До 30 |
3 |
| 30 - 50 |
18 |
| 50 - 70 |
11 |
| 7 0- 90 |
6 |
| Свыше 90 |
2 |
| Итого: |
40 |
Определите характеристики ряда распределения предприятий по выпуску продукции:
1. Средний выпуск продукции, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Сделайте вывод.
2. Структурные средние: моду и медиану, сделайте вывод.
3. С вероятностью 0,954 определите: а) ошибку выборки среднего выпуска продукции и границы, в которых будет находиться средний выпуск продукции предприятий в целом по области; б) пределы доли предприятий с выпуском продукции свыше 70 млн.руб. Сделайте выводы.
РЕШЕНИЕ:
(См. учебное пособие В. М. Гусарова «Статистика», М.: ЮНИТИ - ДАНА, 2003, с.59-62, с.68-80, с.90-104).
1) Рассчитаемсредний выпуск продукции на одно предприятии
по средней арифметической взвешенной для интервального ряда распределения,
используя в расчетах способ моментов.
а) На первом этапе определим величины открытых интервалов (первый и последний), условно приравняв их к величинам примыкающих интервалов (второй и предпоследний), и найдем неизвестные границы интервалов. По значениям признака второго интервала величина интервала составляет: 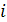 =50-30 = 20 (млн. руб.), из предпоследнего интервала: =50-30 = 20 (млн. руб.), из предпоследнего интервала: 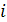 =90-70=20 (млн. руб.). Отсюда неизвестная (нижняя) граница первого интервала равна разности между верхней границей и величиной интервала: 30-20=10; неизвестная (верхняя) граница последнего интервала равна сумме нижней границе этого интервала и величины интервала: 90+20 = 110. =90-70=20 (млн. руб.). Отсюда неизвестная (нижняя) граница первого интервала равна разности между верхней границей и величиной интервала: 30-20=10; неизвестная (верхняя) граница последнего интервала равна сумме нижней границе этого интервала и величины интервала: 90+20 = 110.
б) На втором этапе определим центры интервалов (Хц) – в таблице графа 3:
Х1
= (10+30)/2 =20; Х2
= (30+50)/2 =40; Х3
= (50+70)/2 = 60; Х4
= (70+90)/2 = 80; Х5
= (90+110)/2 = 100 (графа 3).
Для вычисления показателей построим расчетную таблицу (таблица5).
Таблица 5
Расчет среднего выпуска продукции и среднего квадратического отклонения способом моментов
| Группы предприятий по выпуску продукции, млн.руб. Х |
Число предприятий
f
|
Расчетные показатели |
| Хц |
Х1
=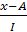
|
Х1
f |
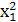 |
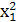 f f |
S |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| До 30(10-30) |
4 |
20 |
-2 |
-8 |
4 |
16 |
4 |
| 30-50 |
15 |
40 |
-1 |
-15 |
1 |
15 |
19 |
| 50-70 |
11 |
60
|
0 |
0 |
0 |
0 |
30 |
| 70-90 |
7 |
80 |
+1 |
+7 |
1 |
7 |
37 |
| Свыше 90 (90-110) |
3 |
100 |
+2 |
+6 |
4 |
12 |
40 |
| Итого |
40 |
- |
- |
-10 |
- |
50 |
- |
в) Средний выпуск продукции
способом моментов
определяется по формуле:
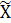 = =
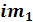 +
A
, +
A
,
где 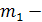 момент первого порядка: момент первого порядка: 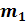 = =
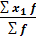 ; ;
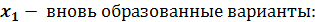
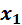 = =
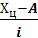 ; А=60 – это варианта, расположенная в середине ряда; ; А=60 – это варианта, расположенная в середине ряда; 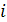 =20 – это величина интервала (для рядов с равными интервалами). =20 – это величина интервала (для рядов с равными интервалами).
Вновь образованные варианты ( ) рассчитаны в графе 4 таблицы. ) рассчитаны в графе 4 таблицы.
Определим условный момент 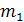 : :
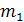 = = 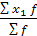 = =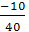 = -0,25; = -0,25;
тогда средний выпуск продукции на одно предприятие в выборочной совокупности составит:
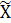 = = 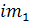 + A = 20 ×(- 0,25) + 60 = 55 (млн. руб.) + A = 20 ×(- 0,25) + 60 = 55 (млн. руб.)
2) Среднее квадратическое отклонение способом моментов
определяется по формуле:
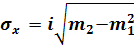 ; ;
где 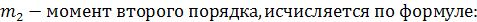  = =
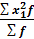 Промежуточные расчеты для момента второго порядка выполнены в графах 6 и7 таблицы. Промежуточные расчеты для момента второго порядка выполнены в графах 6 и7 таблицы.
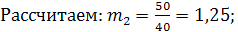 отсюда среднее квадратическое отклонение составит: отсюда среднее квадратическое отклонение составит: 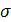 х
=20 х
=20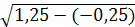 2
= =21,79 (млн. руб.) 2
= =21,79 (млн. руб.)
Дисперсия способом моментов
определяется по формуле: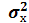 = =
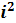 ( (
 - -
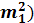 ; ;
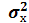 =
(21,79)2
= 474,80 =
(21,79)2
= 474,80
3) Определим коэффициент вариации
. Коэффициент вариации (V) представляет собой удельный вес среднего квадратического отклонения в среднем значении признака:
V= 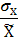 ×100%; V= ×100%; V= 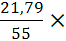 100% = 39,54%. 100% = 39,54%.
Коэффициент вариации дает сравнительную оценку вариации и характеризует однородность совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Выводы:
Средний выпуск продукции по сорока предприятиям области составил 55 млн. руб.
Среднее квадратическое отклонение 21,79 млн. руб. показывает, что выпуск продукции каждого предприятия отклоняется от среднего выпуска продукции всех предприятий в выборке в среднем в ту и другую сторону на 21,79 млн. руб. и колеблется в пределах от 33,21 млн. руб. до 76,79 млн. руб. (55±21,79).
Значение коэффициента вариации 39,54% свидетельствует о значительной степени разнообразия предприятий по выпуску продукции.
4) Определим структурные средние. Мода (Мо)
– наиболее часто встречающееся значение признака в совокупности. В интервальном вариационном ряду с равными интервалами мода находится внутри модального интервала (это интервал с наибольшей частотой) и определяется по формуле:
Mo = 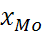 + + 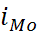 × × 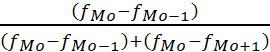
где 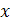 Мо
– нижняя граница модального интервала Мо
– нижняя граница модального интервала
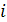 Мо
– величина модального интервала Мо
– величина модального интервала
fМо
– частота модального интервала (наибольшая)
fМо-1
– частота предмодального интервала
fМо+1
– частота послемодального интервала
Мода находится в интервале с наибольшей частотой, т.е. в интервале 30-50, т.к. fМо
= fmax
= 15. Нижняя граница модального интервала ХМо
= 30, интервал модального интервала 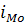 =20, , частота предмодального интервала fМ0-1
= 4, частота послемодального интервала fМо+1
= 11. =20, , частота предмодального интервала fМ0-1
= 4, частота послемодального интервала fМо+1
= 11.
Подставим найденные параметры в формулу моды:
Мо
= 30+20×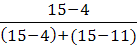 =30+ =30+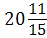 =44,67 (млн. руб.) =44,67 (млн. руб.)
5) Медиана (Ме)
– это вариант, который находится в середине упорядоченного ряда, и делит его на две равные по числу единиц части со значениями признака меньше медианы и со значениями признака больше медианы. В интервальном вариационном ряду медиана находится в медианном интервале, которому соответствует накопленная частота, равная или превысившая полусумму частот ряда, и определяется по формуле:
Me = 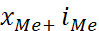 × × 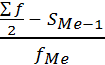
где 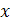 Ме
- нижняя граница медианного интервала Ме
- нижняя граница медианного интервала
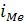 – медианный интервал – медианный интервал
Σf / 2 – полусумма частот ряда
SМе-1
– накопленная частота предмедианного интервала
fМе
– частота медианного интервала
По накопленным частотам в графе 8 определяем, что накопленная частота SМе
= 30 превысила полусумму частот ряда (Σf/2 = 20). Следовательно, нижняя граница медианного интервала 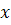 Ме
= 50, медианная частота fМе
= 11, накопленная частота предмедианного интервала SМе-1
= 19. Подставим все параметры в формулу медианы и определим: Ме
= 50, медианная частота fМе
= 11, накопленная частота предмедианного интервала SМе-1
= 19. Подставим все параметры в формулу медианы и определим:
Ме = 50+20×(20-19) / 11 = 50+20×1/11 = 51,82 (млн. руб.)
Выводы:
1. Средний выпуск продукции у большинства предприятий области составляет 44,67 млн. руб. (Мо).
2. У половины предприятий области (50%) средний выпуск продукции не превышает 51,82 млн. руб., а у другой половины (50%) средний выпуск продукции выше 51,82 млн. руб. (Ме).
6) С вероятностью 0,954 определим ошибку выборки
среднего выпуска продукции на одно предприятие и границы
, в которых будет находиться генеральная средняя выпуска продукции предприятий области.
Из условия известно: =40 предприятий – численность выборочной совокупности; =400 предприятий – численность генеральной совокупности (при 10-% выборке); 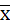 =55 млн. руб.- выборочная средняя; =55 млн. руб.- выборочная средняя; 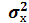 =
474,80 – выборочная дисперсия; Р=0,954 – заданная вероятность ошибки выборки. =
474,80 – выборочная дисперсия; Р=0,954 – заданная вероятность ошибки выборки.
а) Ошибка выборки при механическом способе отбора
определяется по формуле:
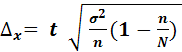 ; ;
где t=2 – коэффициент доверия при вероятности Р=0,954 (коэффициент доверия определяется по математико-статистической таблице значений интеграла вероятностей); отсюда:
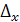 =2 =2 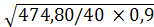 =6,54 млн.руб. =6,54 млн.руб.
Определим нижнюю и верхнюю границы генеральной средней
.
Нижняя граница:
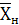 = = 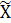 - -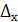 ; ; 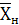 = 55-6,54=48,46 млн.руб. = 55-6,54=48,46 млн.руб.
Верхняя граница:
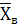 = =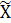 + +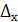 ; ; 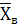 =55+6,54=61,54 млн.руб. =55+6,54=61,54 млн.руб.
Вывод:
С вероятностью 0,954 можно утверждать, что средний выпуск продукции предприятий области в генеральной совокупности будет находиться в пределах от 48,46 млн. руб. до 61,54 млн. руб. или 48,46 млн. руб. ≤ 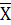 ≤ 61,54 млн. руб. ≤ 61,54 млн. руб.
7) Определим пределы доли предприятий
с выпуском продукции свыше 70 млн. руб.
Выборочная доля
(доля предприятий с выпуском продукции свыше 70 млн. руб. среди обследованных предприятий) равна:
W=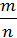 ; ;
где m=8 (это число предприятий с выпуском продукции свыше 70 млн.руб. в выборочной совокупности, определяется по условию задачи); n=40 (численность выборочной совокупности); отсюда выборочная доля: W=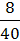 = 0,2 или 20%. = 0,2 или 20%.
Предельная ошибка выборочной доли
определяется по формуле:
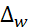 = t = t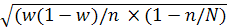 ; ; 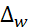 =2× =2× 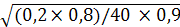 =0,12или 12% =0,12или 12%
Генеральная доля 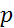 = = 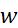 ± ± 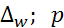 =0,2±0,12 или =0,2±0,12 или 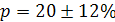 , или , или
8%≤ 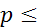 32% 32%
Вывод:
С вероятностью 0,954 можно утверждать, что доля предприятий с выпуском продукции свыше 70 млн. руб. среди всех предприятий области колеблется от 8 до 32%.
ЗАДАЧА 5
Имеются данные, характеризующие списочную численность работников фирмы на начало каждого квартала отчетного года (таблица 6). Используя взаимосвязь показателей динамики, определите:
1. Уровни ряда динамики (округлять до целых) и недостающие в таблице цепные показатели.
2. Среднесписочную численность, средний абсолютный прирост, средние темпы роста и прироста численности персонала за отчетный год. Сделайте вывод.
Таблица 6
| Дата |
Списочная численность персонала, чел. |
Цепные показатели динамики |
| Абсолютный прирост, чел. |
Темп роста, % |
Темп прироста, % |
|1%| прироста, чел. |
| 1.01 |
х |
х |
х |
х |
| 1.04 |
9
|
4,20
|
| 1.07 |
99,6
|
| 1.10 |
0,9
|
| 1.01 следующего года |
436
|
РЕШЕНИЕ (
представим в аналитической таблице 7)
(См. учебное пособие В. М. Гусарова «Статистика», М.: ЮНИТИ - ДАНА, 2003, с.106-109, с.113-128).
1. Используя исходные формулы расчета аналитических показателей динамики и их взаимосвязь, определим уровни ряда динамики и недостающие в таблице цепные показатели.
1) Формула абсолютного содержания 1-го % прироста
: 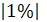 = =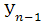 /100, где n – это число уровней ряда динамики. /100, где n – это число уровней ряда динамики.
На 1.04 этот показатель составил: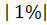 =4,20; отсюда недостающий уровень на начало года =4,20; отсюда недостающий уровень на начало года 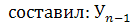 = =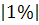 ×100 = 4,20×100 = 420 чел. ×100 = 4,20×100 = 420 чел.
2) Формула абсолютного прироста
: 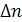 = = 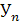 - - 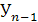 . Абсолютный прирост на 1.04 составил: . Абсолютный прирост на 1.04 составил: 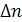 = 9 , отсюда недостающий уровень на 1.04 составил: = 9 , отсюда недостающий уровень на 1.04 составил:
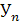 = = 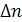 + +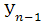 = 420 + 9 = 429 чел. = 420 + 9 = 429 чел.
3) Формула цепного темпа роста
: 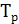 = =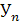 / /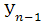 ×100 . На 1.07 темп роста ×100 . На 1.07 темп роста 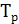 =99,6%; отсюда недостающий уровень на 1.07 составил: =99,6%; отсюда недостающий уровень на 1.07 составил:
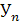 = =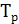 × ×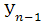 / 100 = 0,996 × 429 = 427 чел. / 100 = 0,996 × 429 = 427 чел.
Таблица 7
Динамика списочной численности персонала фирмы за отчетный год
| Дата |
Списочная численность персонала, чел. |
Цепные показатели динамики |
| Абсолютный прирост, чел. |
Темп роста, % |
Темп прироста, % |
|1%| прироста, чел. |
| 1.01 |
420 |
х |
х |
х |
х |
| 1.04 |
429 |
9
|
102,1 |
2,1 |
4,20
|
| 1.07 |
427 |
-2 |
99,6
|
-0,4 |
4,29 |
| 1.10 |
431 |
4 |
100,9 |
0,9
|
4,27 |
| 1.01 следующего года |
436
|
5 |
101,2 |
1,2 |
4,31 |
4) Формула темпа прироста
: 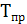 = = 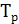 - 100% или - 100% или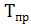 = =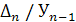 ; известен темп прироста на 1.10: ; известен темп прироста на 1.10: 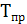 = 0,9%, отсюда на 1.10 темп роста составил: = 0,9%, отсюда на 1.10 темп роста составил: 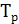 = =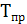 + 100% =0,9 + 100 = 100,9%, по темпу роста определим неизвестный уровень на эту же дату: + 100% =0,9 + 100 = 100,9%, по темпу роста определим неизвестный уровень на эту же дату: 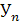 = =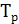 × ×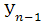 / 100 =1,009×427 = 431 чел. / 100 =1,009×427 = 431 чел.
5) Цепные показатели динамики определим по исчисленным уровням ряда на основе исходных логических формул показателей динамики:
Формула цепного абсолютного прироста
: 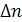 = = 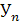 - - 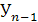
Формула цепного темпа роста
: 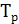 = =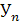 / /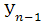 ×100 ×100
Формула цепного темпа прироста
: 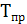 = = 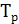 - 100% или - 100% или 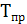 = = 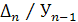
Формула абсолютного содержания 1-го % прироста:
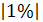 = =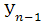 / 100 или / 100 или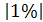 = =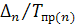
Вывод:
В течение отчетного года каждый квартал, кроме 2-го квартала (на начало 3-го квартала), наблюдается рост численности персонала фирмы как в абсолютном, так и в относительном выражении. Во втором квартале численность персонала сократилась на 2 человека или на 0,4% по сравнению с первым кварталом. Наибольший прирост численности персонала наблюдался в первом квартале, по сравнению с четвертым кварталом предыдущего года численность персонала в первом квартале отчетного года увеличилась на 9 человек или на 2,1%. Абсолютное содержание 1-го % прироста увеличивалось в течение всего отчетного года.
2.
Определим среднесписочную численность, средний абсолютный прирост, средние темпы роста и прироста численности персонала
за отчетный год.
1) Так как уровни ряда динамики представлены на дату, этот ряд является моментным рядом динамики
и его уровни нельзя суммировать. Для расчета среднего уровня моментного ряда применяется формула средней хронологической
:
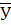 = ( = (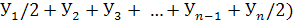 / /
(n-1); отсюда средняя списочная численность
персонала фирмы за отчетный год составила:
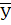 = (420/2 + 429 + 427 + 431 + 436/2) / (5-1) = 429 чел. = (420/2 + 429 + 427 + 431 + 436/2) / (5-1) = 429 чел.
2) Средний абсолютный прирост
рассчитывается по формуле: 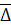 = =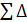 / (n-1); отсюда средний квартальный прирост численности персонала составил: / (n-1); отсюда средний квартальный прирост численности персонала составил:
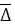 = (9 + (-2) +4 + 5) / 4 = 4 чел. = (9 + (-2) +4 + 5) / 4 = 4 чел.
3) Средний темп роста
рассчитывается двумя тождественными способами по формуле средней геометрической:
1-й способ: 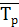 = = 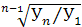 ×100% ×100%
2-ой способ: 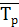 = =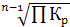 × 100%, где × 100%, где 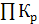 - произведение цепных коэффициентов роста; - произведение цепных коэффициентов роста;
Среднеквартальный темп роста численности персонала фирмы исчислим первым способом:
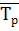 = = 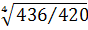 ×100% = 100,94%, соответственно среднеквартальный темп прироста составит 0,94%. ×100% = 100,94%, соответственно среднеквартальный темп прироста составит 0,94%.
Вывод
: Средняя списочная численность персонала фирмы за отчетный год составила 429 человек, в каждом квартале года происходило увеличение списочной численности персонала в среднем на 4 человека или на 0,94 %.
ЗАДАЧА 6
Себестоимость и объем продукции предприятия характеризуются следующими данными:
| Изделия |
Себестоимость единицы продукции, руб. |
Выработано продукции, тыс.шт. |
План
Z0
|
Факт
Z1
|
План
q0
|
Факт
q1
|
| СП-2 |
20 |
23 |
90 |
80 |
| МК-1 |
10 |
9 |
120 |
150 |
Определите:
1. Индивидуальные индексы себестоимости продукции.
2. Общий индекс затрат на продукцию.
3. Общий индекс себестоимости продукции.
4. Общий индекс физического объема продукции.
5. Абсолютное изменение затрат на производство продукции за счет изменения физического объема продукции и себестоимости. Покажите взаимосвязь индексов.
РЕШЕНИЕ
(См. учебное пособие В. М. Гусарова «Статистика», М.: ЮНИТИ - ДАНА, 2003, с.143-162, с.172-179).
1) Индивидуальные индексы
себестоимости продукции определим по формуле:
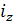 = Z1
/ Z0 = Z1
/ Z0
Подставив числовые значения, получим индивидуальные индексы себестоимости: а) изделия СП-2 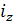 = 23/20 = 1,15 или 115,0%; б) изделия МК-1 = 23/20 = 1,15 или 115,0%; б) изделия МК-1 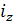 = 9/10 = 0,9 или 90,0%. = 9/10 = 0,9 или 90,0%.
Вывод:
фактическая себестоимость единицы изделия СП-2 выросла на 3 руб. или на 15,0%, а изделия МК-1 снизилась 1 руб. или на 10,0% по сравнению с планом.
2) Общий индекс затрат на продукцию
определим по формуле агрегатного индекса:
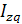 = ΣZ1
q1
/ ΣZ0
q0
= (23×80+9×150) / (20×90+10×120) = 3190/3000 = 1,063 или 106,3%. = ΣZ1
q1
/ ΣZ0
q0
= (23×80+9×150) / (20×90+10×120) = 3190/3000 = 1,063 или 106,3%.
Разность между числителем и знаменателем индекса характеризует изменение затрат на продукцию в абсолютном выражении:
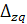 = ΣZ1
q1
- ΣZ0
q0
= 3190-3000 = 190 тыс. руб. = ΣZ1
q1
- ΣZ0
q0
= 3190-3000 = 190 тыс. руб.
ВЫВОД:
фактические затраты на всю произведенную продукцию превысили плановое задание на 6,3% или на 190 тыс. руб.
3) Общий индекс себестоимости продукции
определим по формуле агрегатного индекса:
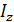 = Σz1
q1
/ Σz0
q1
= (23×80+9×150) / (20×80+10×150) = 3190/3100 = =1,029 или 102,9%. = Σz1
q1
/ Σz0
q1
= (23×80+9×150) / (20×80+10×150) = 3190/3100 = =1,029 или 102,9%.
Абсолютную величину изменения затрат на продукцию
за счет изменения себестоимости получим как разность между числителем и знаменателем общего индекса себестоимости:
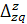 = ΣZ1
q1
– ΣZ0
q1
= 3190-3100 = 90 тыс. руб. = ΣZ1
q1
– ΣZ0
q1
= 3190-3100 = 90 тыс. руб.
Вывод:
фактическая себестоимость всех изделий по сравнению с планом выросла в среднем на 2,9%, вследствие чего затраты на производство продукции увеличились на 90 тыс. руб.
4) Общий индекс физического объема продукции
определим по формуле агрегатного индекса:
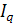 = Σq1
Z0
/ Σq0
Z0
= (80×20+150×10) / (90×20+120×10) = =3100/3000 = 1,033 или 103,3% = Σq1
Z0
/ Σq0
Z0
= (80×20+150×10) / (90×20+120×10) = =3100/3000 = 1,033 или 103,3%
Разность между числителем и знаменателем индекса показывает изменение абсолютной величины затрат на продукцию
за счет изменения физического объема продукции:
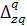 = Σq1
Z0
– Σq0
Z0
= 3100 – 3000 = 100 тыс. руб. = Σq1
Z0
– Σq0
Z0
= 3100 – 3000 = 100 тыс. руб.
Вывод:
физический объем фактически произведенной продукции по сравнению с планом увеличился в среднем на 3,3%, вследствие чего затраты на продукцию выросли на 100 тыс. руб.
Путем подстановки значений рассчитанных индексов проверим их взаимосвязь: 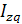 = = 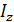 × × 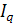 или или 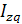 = 1,033 ×1,029 = 1,063 или 106,3%. = 1,033 ×1,029 = 1,063 или 106,3%.
Проверка взаимосвязи абсолютного изменения результативного показателя за счет отдельных факторов:
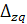 = = 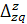 + + 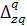 = 90 + 100 = 190 тыс. руб. = 90 + 100 = 190 тыс. руб.
Проверка показала правильность произведенных расчетов.
ЗАДАЧА 7
Имеются данные по предприятию за два периода:
Вид
продукции
|
Выпуск продукции в фактических ценах, тыс. руб. |
Изменение объема выпущенной продукции в отчетном периоде по сравнению с базисным, % |
Базисный
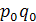
|
Отчетный
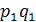
|
А
Б
В
|
562
780
644
|
589
810
677
|
+5,0
+7,2
+3,8
|
Определите общие индексы: физического объема продукции, выпуска продукции, цен. Сделайте вывод.
РЕШЕНИЕ
(См. учебное пособие В. М. Гусарова «Статистика», М.: ЮНИТИ - ДАНА, 2003, с.152-154, с.172-179).
1) Общий индекс физического объема продукции в данном примере нельзя исчислить по формуле агрегатного индекса, так как не достает данных. Известна стоимость выпуска продукции, т.е. результативный показатель за базисный период (q0
P0
) и за отчетный период (q1
P1
).
Так как известно изменение физического объема продукции, можно получить индивидуальные индексы физического объема продукции:
по изделию А: 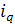 = 100+5 = 105,0% или 1,05; = 100+5 = 105,0% или 1,05;
по изделию Б: 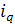 = 100+7,2 = 107,2% или 1,072; = 100+7,2 = 107,2% или 1,072;
по изделию В: 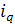 = 100+3,8 = 103,8% или 1,038. = 100+3,8 = 103,8% или 1,038.
В соответствии с исходными данными общий индекс физического объема
продукции рассчитывается по формуле среднего арифметического из индивидуальных индексов:
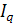 = Σ = Σ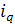 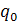 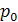 / Σ / Σ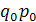 = (1,05×562 +1,072×780 +1,038×644) / (562 + 780 +644) = (1,05×562 +1,072×780 +1,038×644) / (562 + 780 +644)
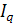 = 2094,8 / 1986 = 1,055 или 105,5%. = 2094,8 / 1986 = 1,055 или 105,5%.
2) Общий индекс выпуска (стоимости) продукции
находим по формуле агрегатного индекса:
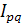 = Σ = Σ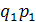 / Σ / Σ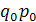 = (589+810+677) / (562+780+644) = 2076/1986 = 1,045 или 104,5%. = (589+810+677) / (562+780+644) = 2076/1986 = 1,045 или 104,5%.
3) Общий индекс цен
определим, используя взаимосвязь индексов:
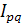 = = 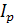 × × 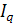 , тогда , тогда 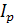 = = 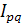 / / 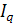 = 1,045/1,055 = 0,991 или 99,1%. = 1,045/1,055 = 0,991 или 99,1%.
Вывод.
В отчетном периоде по сравнению с базисным физический объем производства всей продукции увеличился на 5,5%, цены снизились в среднем на 0,9%, в результате действия этих факторов выпуск продукции вырос на 4,5%.
ЗАДАЧА 8
Имеются следующие данные по трем группам рабочих с разным стажем работы:
| Стаж работы, лет |
Число рабочих |
Средняя заработная плата, руб. |
Среднее квадратическое отклонение заработной платы, руб. |
До 5
5-10
Более 10
|
10
15
25
|
4500
6000
8000
|
120
200
500
|
Определите:
1. Среднюю заработную плату для всей совокупности рабочих.
2. Общую дисперсию и среднее квадратическое отклонение заработной платы.
3. Коэффициент детерминации для оценки доли колеблемости заработной платы в зависимости от изменения стажа работы.
4. С помощью эмпирического корреляционного отношения определите степень влияния стажа работы на вариацию заработной платы. Сделайте выводы.
РЕШЕНИЕ
(представим в расчетной таблице 8)
(См. учебное пособие В. М. Гусарова «Статистика», М.: ЮНИТИ - ДАНА, 2003, с.80-84,).
Таблица 8
Расчет дисперсии групповых средних (межгрупповой дисперсии) средней заработной платы рабочих
Стаж работы лет
Х
|
Число рабо
чих
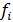
|
Средняя заработная плата, тыс. руб.
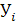
|
Среднее квад
ратическое
отклонение заработной платы, тыс. руб.
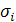
|
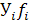 |
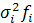 |
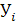 - -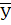 |
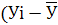 )2
× )2
×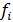 |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
До 5
5-10
Более 10
|
10
15
25
|
4,5
6,0
8,0
|
0,120
0,200
0,500
|
45
90
200
|
0,144
0,600
6,25
|
-2,2
-0,7
1,3
|
48,400
7,350
42,250
|
| Итого |
50 |
- |
- |
335 |
6,994 |
- |
98,000 |
1) Общая средняя
заработная плата рабочих определяется по расчетным данным таблицы 8 по средней арифметической взвешенной:
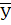 = = 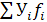 / /  = 335 / 50 = 6,7 тыс. руб. или 6700 рублей. = 335 / 50 = 6,7 тыс. руб. или 6700 рублей.
2) Определим среднюю из групповых дисперсий (
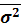 ),
которая характеризует вариацию, возникающую под влиянием случайных факторов, кроме признака-фактора, положенного в основание группировки, так как групповые дисперсии характеризуют лишь случайную вариацию в каждой отдельной группе. Средняя из групповых дисперсий определяется по формуле: ),
которая характеризует вариацию, возникающую под влиянием случайных факторов, кроме признака-фактора, положенного в основание группировки, так как групповые дисперсии характеризуют лишь случайную вариацию в каждой отдельной группе. Средняя из групповых дисперсий определяется по формуле:
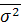 = =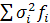 / /  = 6,994 / 50 = 0,1399 = 6,994 / 50 = 0,1399
3) Определим межгрупповую дисперсию (
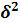 ),
которая отражает вариацию изучаемого результативного признака, возникающую под влиянием признака-фактора, положенного в основание группировки: ),
которая отражает вариацию изучаемого результативного признака, возникающую под влиянием признака-фактора, положенного в основание группировки:
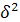 = =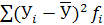 / /  = 98 / 50 = 1,96 = 98 / 50 = 1,96
4) Общая дисперсия
(
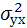 )
характеризует вариацию результативного признака, возникающую под влиянием всех факторов в данной совокупности, и рассчитывается по правилу сложения дисперсий: )
характеризует вариацию результативного признака, возникающую под влиянием всех факторов в данной совокупности, и рассчитывается по правилу сложения дисперсий:
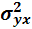 = =
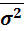 + +
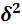
Общая дисперсия заработной платы рабочих составила:  = 0,139 + 1,96 = 2,099 = 0,139 + 1,96 = 2,099
Отсюда среднее квадратическое отклонение
заработной платы по всей совокупности рабочих:
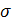 = = 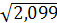 = 1,449 тыс. руб. или 1449 рублей = 1,449 тыс. руб. или 1449 рублей
Вывод:
Средняя заработная плата каждого рабочего отклоняется от общей средней заработной платы всех рабочих в среднем в ту и другую сторону на 1449 рублей и колеблется в пределах от 5251 руб. до 8149 руб.
5) Коэффициент детерминации
показывает долю общей колеблемости результативного признака, вызванную действием факторного признака, положенного в основание группировки, и рассчитывается по формуле:
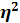 = =
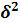 / /
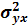
Отсюда, коэффициент детерминации составил:
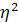 =1,96 / 2,099 = 0,934 или 93,4%. =1,96 / 2,099 = 0,934 или 93,4%.
Вывод:
Различия в уровнях заработной платы рабочих на 93,4% обусловлены стажем работы (факторным признаком) и на 6,6% - влиянием других факторов.
5) Эмпирическое корреляционное отношение
оценивает тесноту зависимости вариации результативного признака (У) от вариации факторного признака (Х), положенного в основание группировки, и принимает значения в интервале 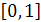 : чем ближе к 1, тем теснее связь между признаками, и наоборот. Эмпирическое корреляционное отношение – это квадратный корень из коэффициента детерминации: : чем ближе к 1, тем теснее связь между признаками, и наоборот. Эмпирическое корреляционное отношение – это квадратный корень из коэффициента детерминации:
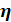 = =
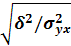
Отсюда, эмпирическое корреляционное отношение составило:
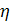 = = 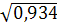 = 0,966 = 0,966
Вывод:
Эмпирическое корреляционное отношение близко к 1, что означает сильную зависимость вариации заработной платы рабочих от стажа.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И СХЕМЫ РЕШЕНИЙ ПРАКТИЧЕСКИХ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ №2 ПО РАЗДЕЛУ «СТАТИСТИКА ПРЕДПРИЯТИЯ» КУРСА «СТАТИСТИКА»
Пример 1 (задание 2) .
Имеются следующие данные о численности персонала на предприятии за август (табл. 1):
Таблица 1
| Числа месяца |
Состояло по списку каждый день |
Явилось на работу каждый день |
Число целодневных простоев на каждый день |
С 1-го по 4-е
С 7-го по 8-е
С 9-го по 11-е
С 14-го по 18-е
С 21-го по 25-е
С 28-го по 31-е
|
420
422
430
432
425
431
|
420
420
427
430
420
431
|
-
97
-
-
21
-
|
Выходные и праздничные дни месяца: 5,6,12,13,19,20,26,27. Определите среднесписочную численность, среднюю явочную численность, среднее число фактически работавших за март и коэффициент использования средней списочной численности.
Решение:
1) Средняя списочная численность работников в августе составила:
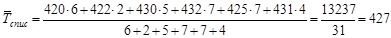 чел. чел.
2) Средняя явочная численность работников в августе составила:
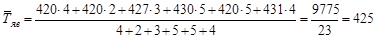 чел. чел.
3) Среднее число фактически работавших в августе составило:
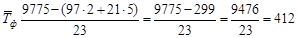 чел. чел.
4) Коэффициент использования списочного состава:
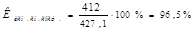
Вывод:
Ежедневно в списках предприятия за август в среднем числилось 427 человек; ежедневно на работу являлось в среднем 425 человек; среднее число фактически работавших каждый день в августе составляло 412 человек. Списочный состав в августе использовался на 96,5%, т.е. средняя численность фактически работавших на 3,5% меньше среднесписочной численности.
Пример 2 (задание 3.)
По предприятию имеются следующие данные за два месяца (таблица 2):
Таблица 2
| Показатели |
Апрель |
Май |
Выпуск продукции, в сопоставимых ценах, тыс.руб.
Среднесписочная численность ППП, чел.
в том числе рабочих, чел.
Отработано рабочими, чел.-дней.
Отработано рабочими, чел.-час.
|
4000
250
200
4000
30800
|
4410
256
210
3990
31521
|
Определите:
1) Уровни производительности труда (среднечасовой, среднедневной, среднемесячный).
2) Динамику производительности труда.
3) Прирост среднемесячной выработки в расчёте на одного работающего за счёт отдельных факторов:
1) доли рабочих в общей численности ППП;
2) средней фактической продолжительности рабочего периода;
3) средней фактической продолжительности рабочего дня.
4) Прирост объёма продукции, полученный за счёт:
1) увеличения численности ППП;
2) роста производительности труда.
Укажите взаимосвязь между показателями уровня производительности труда.
Решение:
1) С целью экономического анализа и рационализации расчётов представим исходные и расчётные показатели в аналитической таблице (таблица 3).
В таблице показана методика расчёта уровней производительности труда (строки 5,6,8,9) и показателей использования рабочего времени (строки 10,11,12). Кроме того, в таблице рассчитаны абсолютные и относительные значения прироста (снижения) указанных показателей (графы 4 и 5).
Таблица 3
Анализ динамики производительности труда и рабочего времени на предприятии за апрель-май
| Показатели |
Обозначение |
Апрель |
Май |
Абсолютное изменение гр.3 – гр.2 |
Индекс динамики %
гр.3 : гр.2
|
| А |
1 |
2 |
3 |
4 |
5 |
| 1. Выпуск продукции, тыс. руб. |
Q |
4000 |
4410 |
+410 |
110,2 |
| 2.Среднесписочная численность ППП, чел. |
T |
250 |
256 |
+6 |
102,4 |
| 3. В том числе рабочих, чел. |
L |
200 |
210 |
+10 |
105,0 |
| 4. Отработанно рабочими, чел.-дней |
- |
4000 |
3990 |
-10 |
99,8 |
| 5. Отработано рабочими, чел.-час. |
- |
30800 |
31521 |
+721 |
102,3 |
| РАСЧЕТНЫЕ ПОКАЗАТЕЛИ |
| 6. Средняя часовая выработка рабочего, руб. (стр 1 : стр 5) |
а |
129,87 |
139,91 |
+10,04 |
107,7 |
| 7. Средняя дневная выработка рабочего, руб. (стр 1 : стр 4 или стр. 6 х стр. 10) |
Wдн
|
1000,00 |
1105,26 |
+105,26 |
110,5 |
| 8. Среднемесячная выработка рабочего, руб. (стр 1 : стр 3 или стр 7 х стр 11) |
Wp
|
20000,0 |
21000,0 |
+1000,0 |
105,0 |
| 9. Среднемесячная выработка одного работника ППП, руб. (стр 1 : стр 2 или стр 8 х стр 12) |
Wпп
|
16000,00 |
17226,56 |
+1226,56 |
107,7 |
| 10.Средняя продолжительность рабочего дня, часов (стр 5 : стр4) |
b |
7,7 |
7,9 |
+0,2 |
102,6 |
| 11.Средняя продолжительность рабочего периода, дней (стр 4: стр 3) |
с |
20,0 |
19,0 |
-1,0 |
95,0 |
| 12.Доля рабочих в общей численности ППП (стр 3 : стр 2) |
d |
0,8000 |
0,8203 |
+0,0203 |
102,5 |
2) В качестве проверки исчисленных показателей используем их взаимосвязь:
1) среднемесячная выработка одного работника в апреле:
Wпппо
=a0
b0
c0
d0
= 129,87∙7,7∙20,0∙0,80≈16000 руб.
2) средняя месячная выработка одного работника в мае:
Wппп1
=а1
b1
с1
d1
=139,91∙7,9∙19,0∙0,82≈17226 руб.
Полученные результаты соответствуют рассчитанным в таблице (строка 9).
3) Аналогичная взаимосвязь существует между индексами показателей.
Индекс средней месячной выработки одного работника:
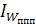 = =
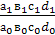 = =
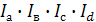 =(1,077∙1,026∙0,95∙1,25)∙100%=107,7%, =(1,077∙1,026∙0,95∙1,25)∙100%=107,7%,
что было рассчитано в таблице (графа 5).
4) Пофакторный анализ изменения средней месячной выработки в расчёте на одного работника ППП выполним на основе метода цепных подстановок.
Изменение средней месячной выработки одного работника ППП
произошло за счёт различных факторов:
1) за счёт роста среднечасовой выработки на одного рабочего на 10,4 руб.:
∆а
Wппп
=(а1
–а0
)в1
с1
d1
=10,04∙7,9∙19,0∙0,8203=1236 руб.
2) за счёт роста средней продолжительности рабочего дня на 0,2 часа:
∆в
Wппп
=а0
(в1
–в0
)с1
d1
=129,87∙0,2∙19,0∙0,8203=404 руб.
3) за счёт сокращения средней продолжительности рабочего периода на 1,0 день:
∆с
Wппп
=а0
в0
(с1
–с0
)d1
=129,87∙7,7∙(-1,0)∙0,8203= - 820 руб.
4) за счёт роста доли рабочих в общей численности персонала на 0,0203:
∆d
Wппп
=а0
в0
с0
(d1
–d0
)=129,87∙7,7∙20.0∙0,0203=406 руб.
Таким образом, прирост средней месячной выработки в расчёте на одного работника ППП составил:
∆Wппп
=∆а
Wппп
+∆в
Wппп
+∆с
Wппп
+∆d
Wппп
=1236+404–820+406 = 1226 руб., что было определено ранее в таблице 3 (строка 9 графа 4).
5) Динамика объёма продукции также зависит от динамики выработки и затрат рабочего времени или численности работников:
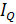 = =
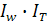
Общий прирост объёма продукции составил:
∆Q=Q1
–Q0
=W1
T1
–W0
T0
=410 тыс. руб. (строка 1 графа 4) в том числе:
1) за счёт интенсивного фактора (средней выработки одного работника ППП):
∆W
Q
(W1
–W0
)T1
=1226,56∙256≈314000 руб.
2) за счёт экстенсивного фактора (средней списочной численности ППП):
∆т
Q
(Т1
–Т0
)W0
=6∙16000=96000 руб.
Совместное влияние обоих факторов привело к увеличению объёма продукции на: 314+96=410 тыс. руб.
Значит, интенсивный фактор обеспечил 76,6% (314:410∙100%) прироста объёма продукции.
Вывод:
1. Среднемесячная выработка в расчёте на одного работника ППП в мае по сравнению с апрелем выросла в целом на 1226 руб., или на 7,7%, в том числе:
1) выросла на 1236 руб. вследствие роста среднечасовой выработки рабочих,
2) выросла на 404 руб. вследствие увеличения средней продолжительности рабочего дня,
3) выросла на 406 руб. из-за увеличения доли рабочих в общей численности работников,
4) снизилась на 820 руб. из-за сокращения средней продолжительности рабочего дня.
2. Объём выпуска продукции в мае по сравнению с апрелем увеличился на 410 тыс. руб. или на 10,2%, в том числе:
1) за счёт изменения интенсивного фактора (роста средней выработки одного работника) прирост продукции составил 314 тыс.руб. или 76,6% от общего размера прироста объёма продукции.
2) за счёт изменения экстенсивного фактора (увеличения средней списочной численности ППП) объём продукции увеличился на 96 тыс.руб., что составило 23,4% общего прироста объёма продукции.
Пример 3 (задание 4).
По предприятию имеются следующие данные (табл. 4):
Таблица 4
| Показатели |
Базисный период |
Отчётный период |
1. Объём продукции, тыс. руб.
2. Фонд заработной платы, тыс. руб.
3. Средняя списочная численность работников, чел.
|
2600
1400
210
|
2700
1380
200
|
Требуется проанализировать динамику заработной платы, производительности труда и фонд оплаты труда. Выполнить факторный анализ изменения фонда оплаты труда.
Решение:
С целью экономического анализа исходные и расчётные показатели представим в аналитической таблице 5.
Таблица 5
Анализ динамики заработной платы, производительности труда и фонда заработной платы
| Показатели |
Обозначение |
Периоды |
Абсолютное отклонение |
Индекс динамики, % |
| Базисный |
Отчётный |
| А |
1 |
2 |
3 |
4 |
5 |
| 1.Объём продукции, тыс. руб. |
Q |
2600 |
2700 |
+100 |
103,84 |
| 2.Фонд заработной платы, тыс. руб. |
F |
1400 |
1380 |
-20 |
98,57 |
| 3.Средняя списочная численность работников, чел. |
T |
210 |
200 |
-10 |
95,23 |
| РАСЧЕТНЫЕ ПОКАЗАТЕЛИ |
4.Выработка на одного человека, тыс. руб.
(стр.1 : стр. 3)
|
W |
12,381 |
13,500 |
+1,119 |
109,03 |
| 5. Средняя заработная плата на одного человека, тыс. руб. (стр. 2 : стр. 3) |
F |
6,667 |
6,900 |
+0,233 |
103,49 |
| 6.Коэффициент опережения темпа роста производительности труда по сравнению с темпом роста уровня заработной платы, % |
Коп
|
- |
105,35 |
- |
- |
1) По исходным данным определим:
1) уровни и динамику производительности труда:
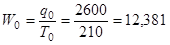 тыс. руб./чел.; тыс. руб./чел.;
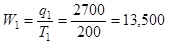 тыс. руб./чел.; тыс. руб./чел.;
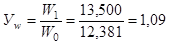 или 109% (стр. 4 табл. 5) или 109% (стр. 4 табл. 5)
2) уровни и динамику средней заработной платы:
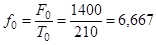 тыс. руб./чел.; тыс. руб./чел.;
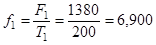 тыс. руб./чел.; тыс. руб./чел.;
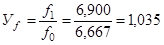 или 103,5% (стр. 5 табл. 5) или 103,5% (стр. 5 табл. 5)
2) Коэффициент опережения темпов роста производительности труда по сравнению с темпами роста заработной платы:
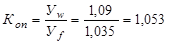 или 105,3% или 105,3%
3) Фонд заработной платы уменьшился на 20 тыс. руб. или на 1,43% (стр. 2 табл. 5), в том числе абсолютное изменение фонда заработной платы составило:
1) за счёт роста уровня средней заработной платы на 0,233 тыс. руб. прирост фонда заработной платы составил:
∆Ff
=(f1-
f0
)∙T1
=0,233∙200=46,6 тыс. руб
.
2) за счёт уменьшения численности работников на 10 человек экономия фонда оплаты труда составила:
∆Fт
=(Т1
–Т0
)∙f1
=-10∙6,667≈ - 66,6 тыс. руб.
4) Экономия фонда заработной платы на 66,6 тыс. руб. обусловлена изменением объема выпуска продукции и ростом производительности труда:
1) прирост фонда заработной платы вследствие роста объёма продукции на 3,8% составил:
∆Fтq
=F0
(Уq
-1)=1400∙(1,0384-1)=53,8
тыс. руб.
2) уменьшение фонда заработной платы вследствие роста производительности труда на 9,0%: составило:
∆Fтw
=F0
(Ут
-Уq
)=1400∙(0,952-1,038)=
- 120,4 тыс. руб.
5)
Проверим аддитивную взаимосвязь показателей:
∆F=∆Ff
+∆Fт
=46,6-66,6=-20 тыс. руб.
∆Fт
=∆Fтq
+∆Fтw
=53,8-120,4=-66,6 тыс. руб.
Результаты факторного анализа изменения фонда оплаты труда представим в таблице 6.
Таблица 6
Анализ изменения фонда заработной платы (факторы – средняя заработная плата, численность персонала, объём продукции, производительность труда)
| Показатели |
Базисный период |
Отчётный период |
| А |
1 |
2 |
1. Средняя заработная плата. руб. / чел.
2. Средняя списочная численность работников, чел.
3. Объём продукции, тыс. руб.
4. Производительность труда, руб. / чел.
|
6667
210
2600
12381
|
6900
200
2700
13500
|
5. Экономия фонда заработной платы, всего, тыс. руб. в том числе:
а) прирост за счёт роста средней заработной платы
|
-20
+46,6
|
| б) прирост за счёт роста объёма продукции |
+53,8 |
| в) экономия за счёт роста производительности труда |
-120,4 |
Вывод:
Результаты проведённого анализа позволяют сделать в целом благоприятные выводы по предприятию: наблюдается прирост объёма продукции на 3,8% при снижении численности работников на 4,8%.
Прирост производительности труда составил 9,0% при росте уровня заработной платы на 3,5%, что свидетельствует о положительной ситуации на предприятии: уровень заработной платы соответствует труду работников.
Экономия фонда оплаты труда составила 1,4% или 20 тыс. руб., то естьй можно сказать, что на его экономию повлияли как уменьшение численности работников на 10 человек, так и увеличение производительности труда на 1119 руб./чел.
Рост уровня средней заработной платы на 233 руб. и объёма продукции на 100 тыс. руб. вызвали перерасход фонда оплаты труда на 46,6 тыс. руб. и на 53,8 тыс. руб. соответственно. В то же время снижение численности персонала на 10 чел. (4,8%) и рост производительности труда на 1119 руб. (9,0%) позволили сэкономить фонд заработной платы на 120,4 тыс. руб. Основным фактором, оказавшим влияние на экономию фонда заработной платы является рост производительности труда.
Учебно-методическое обеспечение
1.
Основная литература
2. Гражданский Кодекс РФ. Части 1 и 2.
3. Белозерова Е. А. Статистика: практикум по теории статистики. Учебное пособие/ Под ред. Е. А. Белозеровой - Омск: ФСГУТ и КД в г. Омске, 2007-187 с.
4. Белозерова Е. А. Статистика предприятия. Учебное пособие (1 часть)/ Е. А. Белозерова-Омск: Филиал ГОУ ВПО «СГУТ и КД» в г. Омске Омской области, 2010-96с.
5. Гусаров В.М. Статистика. Учебное пособие для вузов. М.: ЮНИТИ-ДАНА, 2002-463 с.
6. Гусаров, В. М., Кузнецова Е. И. Статистика [Текст]: учеб. пос. для ВУЗов /В.М. Гусаров, Е.И. Кузнецова. - 2-е изд., перераб. и доп.- М.: ЮНИТИ-ДАНА, 2008.- 479 с.
7. Салин, В. Н. Социально-экономическая статистика [Текст]: учебник / В.Н. Салин, Е.П. Шпаковская.- М.: Юристъ, 2001.-560 с.
8. Теория статистики. Учебник под ред. Р.А. Шмойловой. М.: Финансы и статистика, 2002-416 с.
2.
Дополнительная литература
1. Адамов, В.Е. Экономика и статистика фирм [Текст]: учебник / В.Е. Адамов, С.Д. Ильенкова, Т.П. Сиротина. - М.: Финансы и статистика, 2002 - 288 с.
2. Белозерова Е. А. Статистика: Методические указания по выполнению контрольных работ/ Сост. Е. А. Белозерова – Омск: ФСГУТ и КД в г. Омске, 2004-37 с.
3. Белявский И.К. Статистика рынка товаров и услуг : Учебник – М. : Финансы и статистика, 2001-656с.
4. Васильева, Э. К. Статистика [Текст]: учебник / Э.К. Васильева, В.С. Лялин. - М.: ЮНИТИ - ДАНА, 2007 - 399 с.
5. Вахрушина М.А. Управленческий анализ : Учеб.пособие.-5 е-изд, стер.-М.: Изд-во”Омега –Л”, 2008-399с.
6. Вуколов, Э. А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTIKA и EXCEL [Текст]: учеб. пос. / Э.А. Вуколов - М.: ФОРУМ: ИНФРА-М, 2004 - 464 с.
7. Гиляровская, Л. Г. Комплексный экономический анализ хозяйственной деятельности [Текст]: учебник. / Л.Г. Гиляровская, Д.В. Лысенко, Д.А. Ендовицкий- М.: ТК Велби, Изд-во Проспект, 2008-360 с.
8. Голуб, Л. А. Социально-экономическая статистика [Текст]: учеб. пос. / Л.А. Голуб.- М.: Гуманит.изд.центр ВЛАДОС, 2001.- 272 с.
9. Елисеева, И. И. Статистика [Текст]: учебник / И.И. Елисеева. - М.: Проспект, 2003.- 448 с.
10. Иванов, Ю. Н. Экономическая статистика [Текст]: учебник / Ю.Н. Иванов, Т.А. Хомченко, Б.Т. Рябушкин. – М.: ИНФРА-М, 2008-480 с.
11. Кнышова, Е. Н. Экономика организации [Текст]: учебник / Е.Н. Кнышова, Е.Е. Панфилова. – М.: ФОРУМ: ИНФРА-М, 2005.- 336 с.
12. Мелкумов Я. С. Социально-экономическая статистика: Учеб. Пособие. – М.: ИНФРА – М, 2009. – 236 с. – (Высшее образование).
13. Общая теория статистики. Учебник под ред. И.И. Елисеевой. М.: Финансы и статистика, 2004-656 с.
14. Общая теория статистики. Учебник. М.Р. Ефимова, Е.В. Петрова, В.Н. Рябцев. М.: ИНФРА, 2000-416 с.
15. Октябрьский, П. Я. Статистика [Текст]: учебник / П.Я. Октябрьский. – М.: Проспект, 2003-328 с.
16. Практикум по теории статистики. Учебное пособие под ред. Р.А. Шмойловой. М.: ИНФРА, 2000-560 с.
17. Практикум по общей теории статистики. Учебное пособие. М.Р. Ефимова и др. М.: Финансы и статистика, 1999-336 с.
18. Социально-экономическая статистика: практикум под ред. В.Н. Салина, Е.П. Шпаковской. Учебное пособие. М.: Финансы и статистика, 2004-192 с.
19. Статистика: учебник/ Л.П. Харченко, В. Г. Ионин, В. В. Глинский и др.; под ред. Канд. Экон. Наук, проф. В. Г. Ионина. – 3-е изд., перераб. И доп. – М.: ИНФРА – М, 2010. – 445 с. – (Высшее образование)
20. Савицкая, Г. В. Теория анализа хозяйственной деятельности [Текст]: учеб. пос. / Г.В. Савицкая. – М.: ИНФРА-М, 2007.- 288 с.
21. Савицкая, Г. В. Методика комплексного анализа хозяйственной деятельности [Текст]: Краткий курс / Г.В. Савицкая. – 3-е изд., испр. и доп.- М.: ИНФРА-М, 2006.- 320 с.
22. Салин, В. Н. Статистика финансов [Текст]: учебник / В.Н. Салин.- М.: Финансы и статистика, 2002.- 816 с.
23. Скамай Л.Г. Трубочкина М.И. Экономический анализ деятельности предприятия : Учебник – М.: ИНФРА-М, 2007.-296с.
24. Статистика. Учебник под ред. И.И. Елисеевой. М.: Проспект, 2003-448 с.
25. Статистика финансов. Учебник под ред. В.Н. Салина. М.: Финансы и статистика, 2002-816 с.
26. Чернов В.А Экономический анализ : торговля, обшественное питание, туристический бизнес : Учебное пособие для вузов - М. : ЮНИТИ – ДАНА, 2003 -276 с.
27. Вопросы статистики. Ежемесячный научно-информационный журнал Госкомстата РФ. М.: Финансы и статистика.
28. Еженедельники: газеты «Экономика и жизнь», «Финансовая газета».
29. Вопросы статистики. Ежемесячный научно-информационный журнал. Федеральная служба по статистике. – М.: Финансы и статистика.
30. Российский статистический ежегодник [Текст]: Федеральная служба по статистике. – М.: Финансы и статистика.
31. Россия в цифрах [Текст]: краткий сборник (ежегодник). Федеральная служба по статистике.- М.: Финансы и статистика.
32. www.aup.ru Административно-Управленческий портал – Публикации по экономике, финансам, менеджменту и маркетингу.
33. www.econline.hl.ru Экономикс он-лайн. Сборник ресурсов по экономике, менеджменту и т.п.
34. www.smartcat.ru/catalogue.shtml Каталог библиотеки Кот Ученый. Все «свежее» и оригинальное.
35. www.statsoft.ru/home/download/textbook/ Учебник по статистике
36. Интернет-сай Омскстата: www.omsk.gks.ru
37. Интернет-сайт Росстата: www.gks.ru
|