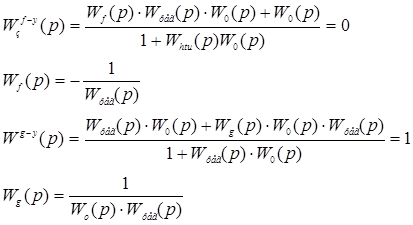Курсовая работа: Синтез астатических систем
|
Название: Синтез астатических систем Раздел: Рефераты по информатике, программированию Тип: курсовая работа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Федеральное агентство по образованию РФ ГОУ ВПО "Московский Государственный Текстильный Университет им. А.Н. Косыгина" ФИТАЭ Кафедра автоматики и промышленной электроники Курсовая работа Тема: "Синтез астатических систем" Дисциплина: "Теория Автоматического Управления" Москва 2009 Исходные данные:
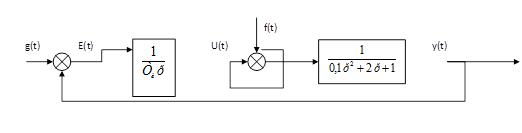
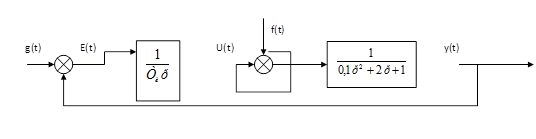
ПИ-закон 1. По заданной системе уравнений получить передаточную функцию объекта управления и составить структурную схему замкнутой САУ, считая регулятор звеном с входной величиной Е, выходной U и передаточной функцией
2. Выбрать регулятор таким образом, чтобы система обладала свойством астатизма по отношению к постоянному задающему g(t) и возмущающему f(t) воздействию. Для того чтобы система обладала астатизмом необходимо выполнение условия – величина установившейся ошибки по заданию и возмущению должна быть равна 0. Проверим это условие на регуляторах: · Выбираем П – регулятор
Т.к. величина установившейся ошибки не равна нулю, то система не обладает астатизмом,, а следовательно считать ошибку по каналу f-E нет необходимости. · Выбираем И – регулятор
Обе ошибки равны нулю следовательно система с И - регулятором является астатической. Данный регулятор нам подходит · Проверим наш ПИ – регулятор
Система так же является астатической, что является тем, что выбранный нами ПИ – регулятор подходит к условию задания. 3. Найти область значений постоянной времени регулятора для И – закона управления, обеспечивающих устойчивость системы.
Найдем передаточную функцию замкнутой системы по каналу g-y и затем выделим ее характеристическое уравнение.
Характеристическое уравнение Q(p):
Уравнение 3 порядка, следовательно, для устойчивости системы необходимо чтобы произведение внутренних коэффициентов характеристического уравнения было больше произведения внешних коэффициентов.
Следовательно область значений 4. Для И – закона регулирования найти минимальную возможную величину установившейся ошибки, если g(t)=2t и f(t)=-3t. Для определения минимальной установившейся ошибки нам необходимо узнать при каком значении постоянной времени система находится на границе устойчивости. Для этого отыщем передаточную функцию и характеристическое уравнение системы с И – регулятором. И затем найдем значение
Находим значение постоянной времени на границе устойчивости:
Найдем величину установившейся ошибки при g(t)=2t и f(t)=-3t
Поскольку задающее воздействие у нас g(t)=2t, то используя преобразование Лапласа получаем:
тогда величина установившейся ошибки будет
Подставляем полученное значение
Найдем ошибку по каналу f-E
Подставляем Тогда 5. Построить, с использованием ЭВМ, область устойчивости, на плоскости, параметров регулятора при использовании ПИ – закона, обосновать возможность и путь получения допустимой установившейся ошибки при Для построение области устойчивости необходимо найти характеристическое уравнение передаточной функции для данного регулятора.
Отсюда:
Запишем условие, при котором система находится на границе устойчивости:
Выразим зависимость
Строим область устойчивости по по лученной зависимости:
Таким образом выбирая значения параметров регулятора над границей устойчивости – мы получаем устойчивую систему, и наоборот. 6. Вычислить значения параметров ПИ – регулятора, обеспечивающих устойчивость и установившуюся ошибку в системе = 0,06 при g(t)=2t и f(t)=0
Поскольку возмущение f(t)=0, то для этого найдем передаточную функцию замкнутой системы по каналу g-E
По условию
Таким образом для получения в системе установившейся ошибке равной 0,06 необходимо задать параметру постоянной времени значение 0,03. 7. Для интегрального закона регулирования и начальных условий Для решения мы будем использовать метод Мондельштама. Для этого нам необходимо найти передаточную функцию замкнутой системы и взять характеристическое уравнение:
Получаем уравнение:
Поочередно умножаем его на
Интегрируем полученное уравнение по частям
Получаем:
Интегрируем полученное уравнение по частям
Получаем:
Из полученных уравнений составим систему уравнений:
Выбираем 8. Для найденного в пункте 7 значения постоянной времени регулятора построить с помощью ЭВМ вещественную частотную характеристику P(ω), приняв входным воздействием g(t) и входной координатой E(t)/ Для нахождения вещественной характеристики нам понадобится передаточная функция замкнутой системы по каналу g-y.
Перейдем в частотную область p=jω:
Домножаем на сопряженное знаменателю число и получаем:
Отделяем действительную часть U(ω):
При
9. По вещественной характеристике P(ω) пункта 8 построить переходной процесс E(t) при единичном ступенчатом изменении g(t) и нулевых начальных условиях методом трапециидальных частотных характеристик. Для построения переходного процесса нам необходимо разбить получившуюся вещественную характеристику на трапеции и построить переходный процесс для каждой из полученных трапеций.
1-я трапеция
2-я трапеция
3-я трапеция
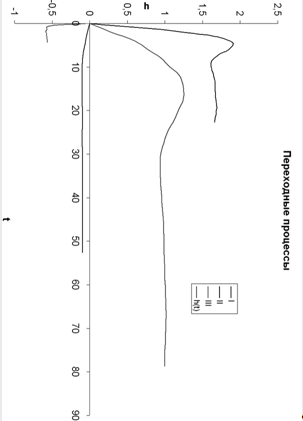
Суммируем графически полученные процесы и получаем
10. Определить время регулирования и максимальное перерегулирование в системе.
11. Разработать и начертить структурную схему комбинированной САУ, инвариантной по отношению к контролируемому возмущению Привести передаточную функцию устройства управления. Проверить выполнение условия инвариантности.
Условия инвариантности:
При выборе корректирующих звеньев в виде обратных передаточных функций возникает проблема. Она обычно связана с тем, что порядок числителя корректирующего звена становится больше порядка знаменателя. Это означает, что частотные характеристики таких звеньев являются расходящимися, что говорит о том, что физически такие звенья нереализуемы. В тех случаях, когда корректирующие звенья применять необходимо, порядок числителя этих звеньев искусственно приравнивают к порядку знаменателя, отбрасывая в числители высшие порядки. 12. Предложить и обосновать методы компенсации действия неконтролируемых возмущений, если известен класс функций, которыми они описываются. астатический автоматический управление моделирование программа
Решить проблему инвариантности можно, если известна предварительная информация о классе возмущающих воздействий. В частности, если известен математический аппарат, описывающий функцию f(t), заданный в виде решения некоторого дифференциального уравнения. Процедура синтеза предусматривает: 1. восстановление вида дифференциального уравнения по заданному решению; 2. получение характеристического уравнения; 3. выбор передаточной функции регулятора, в которой знаменатель совпадает с видом полученного характеристического уравнения. Числитель передаточной функции регулятора выбирается того же порядка, что и знаменатель; 4. неизвестные коэффициенты числителя передаточной функции регулятора определяются из условий устойчивости замкнутой системы. 13. Провести моделирование в программе MatLab. Определить настройки регулятора, обеспечивающего минимизацию времени регулирования.
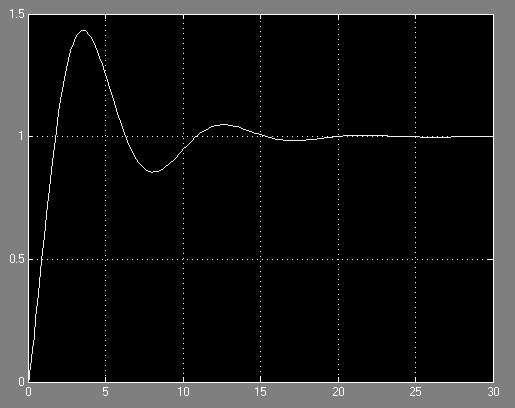
При нулевом задающем воздействии со значением регулятора, полученными в 7 пункте:
При единичном задающем воздействии:
Для снижения времени регулирования можно немного увеличить значения регулятора Так же значительно уменьшает время регулирование и
Список используемой литературы · Лекции по курсу ТАУ, Румянцев Ю.Д. · "Теория автоматического управления", Воронов А.А. · "Теория систем автоматического управления", Бесекерский В.А. Приложение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||









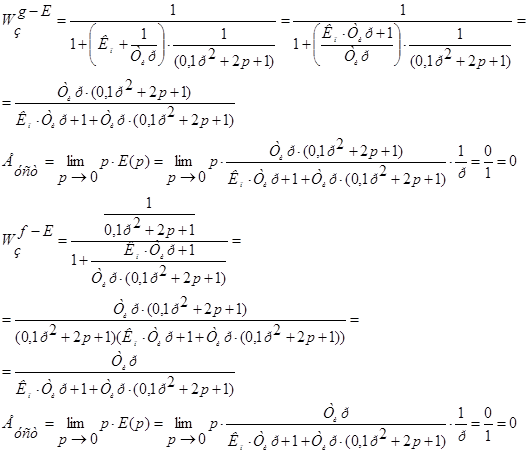














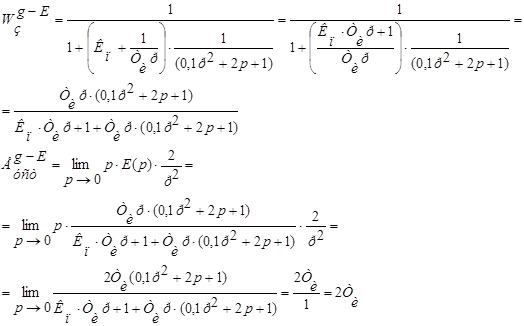

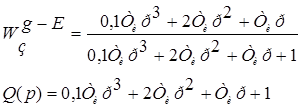







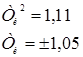




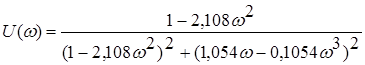








 , если
, если  , если
, если