Оглавление
Введение
1. Теоретическое обоснование методологий демографического прогнозирования:
1.1 Понятие и сущность демографических процессов
1.2 Сущность и содержание технологии социального прогнозирования в сфере демографических процессов
2. Прогнозирование демографических процессов Оренбургской области методами экстраполяции
2.1 Нахождение прогнозных значений методом скользящей средней.
2.2 Нахождение прогнозных значений методом экспоненциального сглаживания.
2.3 Нахождение прогнозных значений методом наименьших квадратов.
Заключение
Список используемой литературы
Приложение 1
Приложение 2
Приложение 3
Введение
Становление рыночных отношений сопровождается формированием нового хозяйственного механизма, в котором важная роль отводится прогнозированию и планированию экономических процессов на различных территориальных уровнях. Демографические прогнозы лежат в основе любого социального прогнозирования и планирования. В самом деле, что бы мы ни планировали на перспективу: развитие производства конкретных товаров или услуг, социальной структуры общества, включая ее структуру по размерам и составу семей, любые социальные процессы — во всех случаях, очевидно, нам прежде всего нужно будет узнать число и состав будущих участников этих социальных процессов по полу и возрасту, поскольку эти «параметры» людей оказывают сильное влияние на характер и интенсивность их деятельности и, соответственно, на характер и интенсивность социальных процессов.
Огромное влияние на развитие экономики, социальной сферы оказывает возрастная структура населения. С увеличением доли лиц трудоспособного возраста в общей численности населения увеличиваются, при прочих равных условиях, темпы, масштабы социально-экономического развития, и наоборот.
Это происходит потому, что влияние демографического фактора проявляется прежде всего посредством реализации трудового потенциала населения, который определяется численностью трудовых ресурсов, их составом, структурой – профессиональной, квалификационной, образовательной и др. Формирование трудового потенциала осуществляется в процессе воспроизводства населения. Управление воспроизводством населения осуществляется посредством разработки и реализации демографической политики, основу которой образуют демографические прогнозы. Демографическая политика – это совокупность социальных, экономических, юридических и других мероприятий, направленных на изменение процесса воспроизводства населения. Например, меры поощрения деторождения (пособия и др.) или его сдерживание. Демографическая политика тесно связана с социальной политикой.
Целью данной курсовой работы является исследование методологии построения демографических прогнозов и практическая реализация технологий прогнозирования на основе имеющихся статистических данных о демографических процессах в Оренбургской области.
Выделим следующие задачи исследования:
- Описать методы, используемые при прогнозировании демографических процессов;
- Построить региональный прогноз демографических показателей: численности постоянного населения, естественного и миграционного прироста (убыли) населения, используя методы экстарполяции;
- Проанализировать полученные результаты, сделать вывод о том какой из методов позволяет получить наиболее достоверные результаты.
Таким образом, в качестве объекта исследования выступает население Оренбургской области, а в качестве предмета – показатели, характеризующие движение населения в абсолютном исчислении.
Методологической базой работы является теория анализа временных рядов.
Работа состоит из введения, двух глав, заключения и трех приложений.
1.
Теоретическое обоснование методологий демографического прогнозирования
1.1
Понятие и сущность демографических процессов
Демография — наука о закономерностях воспроизводства населения, о зависимости его характера от социально-экономических, природных условий, миграции, изучающая численность, территориальное размещение и состав населения, их изменения, причины и следствия этих изменений и дающая рекомендации по их улучшению.
История демографической науки долгое время была связана с развитием эмпирической формы познания, ограничиваясь сбором, обработкой и интерпретации данных о населении в соответствии с практическими потребностями. Выполнение этой функции сопровождалось постоянным совершенствованием методов исследования.
Термин «демография» появился в 1855 г. в названии книги французского ученого А. Гийяра «Элементы статистики человека, или Сравнительная демография». Он рассматривал демографию в широком смысле как «естественную и социальную историю человеческого рода» или более узко как «математическое познание населений, их общего движения, физического, гражданского, интеллектуального и морального состояния».
Официальное признание понятие «демография» получило в наименовании Международного конгресса гигиены и демографии, проходившего в Женеве в 1882 г.
Демография имеет свой четко очерченный объект исследования — население. Демография изучает численность, территориальное размещение и состав населения, закономерности их изменений на основе социальных, экономических, а также биологических и географических факторов.
Единицей совокупности в демографии является человек, который обладает множеством признаков — пол, возраст, семейное положение, образование, род занятий, национальность и т. д. Многие из этих качеств меняются в течение жизни. Поэтому население всегда обладает такими характеристиками, как численность и возрастно-половая структура, семейное состояние. Изменение в жизни каждого человека приводит к изменениям в населении. Эти изменения в совокупности составляют движение населения.
Обычно движение населения подразделяют на три группы:
· естественное
Включает в себя брачность, рождаемость, смертность, изучение которых является исключительной компетенцией демографии.
· миграционное
Это совокупность всех территориальных перемещений населения, которые в конечном счете определяют характер расселения, плотности, сезонную и маятниковую подвижность населения.
· социальное
Переходы людей из одних социальных групп в другие. Этот вид движения определяет воспроизводство социальных структур населения. И именно эта взаимосвязь воспроизводства населения и изменений в социальной структуре изучается демографией.
«Естественная» или «биологическая» сущность народонаселения проявляется в его способности к постоянному самовозобновлению в процессе смены поколений в результате рождений и смертей. И этот непрерывный процесс называется воспроизводством населения.
Процессы рождаемости, смертности, а также брачности и разводимости, будучи составными частями воспроизводства населения, называются демографическими процессами.
Для изучения демографических процессов используют систему статистических показателей: все эти показатели имеют, как правило, количественное выражение, в основе которых лежат измерения демографических явлений и процессов.
Демографический анализ — основной метод обработки информации для получения демографических показателей. Наиболее распространены два типа демографического анализа.
Научно обоснованное предвидение основных параметров движения населения и будущей демографической ситуации называется демографическим прогнозом. Рассмотрим основные методы, применяемые для составления прогнозов.
1.2
Сущность и содержание технологии социального прогнозирования в сфере демографических процессов
Демографические прогнозы являются важным элементом комплексного долгосрочного социально-экономического планирования. Практически очень трудно найти какую-либо область экономики и социальной жизни, где бы при долгосрочном планировании не использовались данные демографических прогнозов.
Разработка демографических прогнозов происходит в несколько стадий.
Первая стадия – аналитическая. Ее содержание – анализ демографической ситуации в стране, регионах на начало прогнозируемого периода, оценка демографических результатов развития общества за истекший период, сопоставление их с прогнозными значениями показателей, выявление диспропорций и негативных тенденций, возникших в демографическом развитии страны.
Вторая стадия – целевая. На этой стадии обосновывается состав целей демографического прогноза. В составе целей выделяются по характеру их возникновения две группы целей.
1-ая группа – это цели, достижение которых представляет собой решение тех проблем, которые возникли в демографическом развитии страны истекшего периода.
2-ая группа целей – это цели, достижение которых предопределено изменением демографических условий в прогнозируемом периоде, характером тех требований, которые предъявит развитие экономики и социальной сферы к демографической ситуации страны в прогнозном периоде.
Третья стадия – расчетная. Ее содержание заключается в обосновании системы прогнозных показателей.
С технической точки зрения демографический прогноз выступает обычно в виде так называемого перспективного исчисления населения, т.е. расчета численности и возрастно-половой структуры, построенного на основании данных об изменениях демографических характеристик (численности населения, демографических структур, рождаемости, смертности и т.д.) в прошлом, а также с учетом принимаемых гипотез относительно их динамики в будущем. Такого рода расчеты делаются обычно в нескольких вариантах, при этом задаются границы наиболее вероятных изменений населения.
Обычно прогноз делается в трех вариантах, которые принято называть «нижним», «средним» и «верхним», причем «средний» вариант соответствует как бы наиболее вероятному ходу событий, а «нижний» и «верхний» задают внешние границы динамики демографических показателей. Варианты демографических прогнозов отражают возможное влияние экономических, социальных, экологических, внешнеэкономических, внутриполитических и других факторов на демографическую ситуацию в стране.
Важной характеристикой демографических прогнозов является их достоверность, т.е. соответствие прогнозных характеристик населения и демографических прогнозов тому, какими они будут в действительности. Достоверность демографического прогноза определяется точностью исходной демографической информации, обоснованностью принимаемых гипотез, длительностью прогнозного периода.
Демографические прогнозы разрабатываются на различные периоды времени:
· краткосрочные – на период от 1 до 10 лет;
· среднесрочные – от 10 до 25 лет;
· долгосрочные – от 25 до 50 лет;
· сверхдолгосрочные – свыше 50 лет.
С увеличением срока прогнозирования точность прогнозов снижается. По оценкам специалистов-демографов, наибольшую практическую ценность имеют прогнозы разрабатываемые на период до 20 лет.
Однако велика потребность и в разработке прогнозов с временным горизонтом свыше 20 лет, несмотря на их снижающуюся достоверность.
Она определяется тем, что для управления, регулирования экономическими и социальными процессами в стране, такими, как оптимизация размещения производительных сил, разработка генеральных схем развития городов, регионов, рационализация использования природных, трудовых ресурсов требуется информация, которая может содержаться только в долгосрочных демографических прогнозах.
При разработке демографических прогнозов наиболее часто используют следующие четыре группы методов:
1) методы экстраполяции;
2) экономико-математические методы, позволяющие разработать многофакторные динамические модели;
3) методы передвижки возрастов и когорт;
4) методы экспертных оценок.
Методы экстраполяции
. Широкое их использование при демографическом прогнозировании объясняется тем, что данные процессы в большинстве случаев достаточно инерционны в своем развитии. Методы экстраполяции применяются не только для оценки будущей численности населения, но и для расчета характеристик движения населения (например, коэффициентов рождаемости, смертности, миграции). Общий недостатокпостроенных с помощью методов экстраполяции прогнозов – это то, что они опираются на средние тенденции динамики населения, зачастую игнорируя особенности отдельных половозрастных групп.
Вторая группа методов, достаточно часто используемых при прогнозирование демографического развития - экономико-математические методы
. Итогом их применения являются динамические модели, которые позволяют учесть влияние новых факторов, проявивших себя в последние периоды. Функция исследователя-прогнозиста заключается в том, чтобы из перечня факторов, оказывающих влияние на изучаемый процесс выбрать наиболее значимые и рассчитать параметры многофакторной модели.
В составе факторов, влияющих на характер демографического развития, различают две основные группы:
первая группа - объективные факторы
, на характер действия которых система органов управления повлиять не может, например, сложившиеся традиции, религиозные представления населения, состояние международной обстановки, последствия войн, иных социальных потрясений;
вторая группа - факторы, влияние
которых в большей или меньшей степени управляемо
(например, прогресс в медицинской науке, качество медицинского обслуживания, культурно-образовательный уровень населения, уровень жизни населения по различным аспектам – жилищная обеспеченность, бытовые условия, размер доходов и др.). Влияние каждого фактора рассчитывается отдельно, после чего определяется суммарное взаимодействие всех факторов.
Существует взаимозависимость между различными факторам, т.е. с изменением характера влияния одних факторов изменяется характер влияния других. Поэтому в прогнозных расчетах используются экономико-математические методы, разрабатываются многофакторные динамические модели, в которых значения демографических показателей представлены как функции, а факторы – как аргументы. В интегральной форме совокупное влияние всех факторов может быть выражено в виде следующей формулы:

где 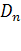 - прогнозное значение демографического показателя; - прогнозное значение демографического показателя; 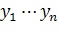 - количественные значения различных факторов в прогнозируемом периоде; - количественные значения различных факторов в прогнозируемом периоде;
n
– количество факторов, учитываемых в расчетах.
В составе прогнозируемых показателей наиболее значимы следующие: численность населения страны по годам прогнозируемого периода, темпы роста численности, структура населения, ее динамика, трудовой, экономический, потребительский потенциалы населения, жизненный фонд населения и др.
Третья группа методов демографического прогнозирования - методы передвижки возрастов
и когорт.
Они позволяют устранить недостаток методов экстраполяции – прогнозирование на основе средней тенденции динамики населения. Эти методы основаны на том, что показатели рождаемости и смертности, миграции существенно различаются у различных половозрастных групп. Основой расчета по методу передвижки возрастов служит коэффициент дожития,
достигнутый различными половозрастными группами, а основа метода когорт – коэффициент рождаемости
, достигнутый различными возрастными группами женщин или когортами.
Четвертая группа методов, достаточно широко применяемых при демографическом прогнозировании – это методы экспертных оценок
. Они незаменимы в случаях недостаточного объема статистической информации об объекте прогнозирования, а также и в случаях, когда в новом периоде на изучаемый процесс начинают оказывать влияние новые факторы, влияние которых изучить по данным за предыдущие периоды невозможно.
Рассмотрим применение методов демографического прогнозирования на примере демографических процессов Оренбургской области.
2. Прогнозирование демографических процессов Оренбургской области методами экстраполяции
В современных условиях развития рыночных отношений, реализации принципов федерализма, становления местного самоуправления возрастает роль региональных демографических прогнозов. Состав демографических факторов, характер их влияния своеобразны для каждого региона. Для одних огромное значение имеет миграционный фактор (Ставропольский край, Ростовская область), для других – природно-климатический (Север России), для третьих – последствия событий прошлых лет (Центральные районы России), для четвертых – национальные особенности (Юг России) и др. Региональные демографические прогнозы разрабатываются на уровне крупных, средних и малых регионов.
В качестве исходных показателей для прогнозирования демографических процессов в Оренбургской области, возьмем показатели:
- численности постоянного населения на 1 января;
- число родившихся и умерших человек за год (естественное движение населения);
- число прибывших и выбывших человек за год (миграционное движение населения), представленные на сайте Федеральной службы государственной статистики РФ.
Рассчитаем прогнозные значения данных показателей, используя методы экстраполяции: скользящих средних, экспоненциального сглаживания, метод наименьших квадратов. Прогноз должен иметь высокую точность, ошибка прогноза будет тем меньше, чем меньше период (срок) упреждения и чем больше база прогноза.
Период (срок) упреждения - это интервал времени, на который разрабатывается прогноз. База прогноза - это статистическая информация за ряд лет, на которую мы опираемся при построении расчетов. Срок упреждения должен составлять не более 1/3 базы прогноза. В данной работе будем использовать базы прогноза за 19-20 лет и находить прогнозные значения на трехлетний период.
Для оценки точности прогнозов, построенных методом экстраполяции, существуют несколько способов.
Таблица 1
Формулы оценки точности прогнозов методом экстраполяции.
| Средняя абсолютная оценка |
Средняя квадратическая оценка |
Средняя относительная ошибка |
Δ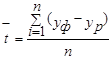
|
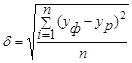 |
ε
=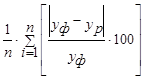 |
| Интерпретация значений |
| Чем ближе к нулю, тем выше точность прогноза |
ε <10 точность высокая
10<ε <20 хорошая
20<ε <50 удовлетворительная
ε >50 неудовлетворительная
|
2.1
Нахождение прогнозных значений методом скользящей средней
Одним из наиболее старых и широко известных методов сглаживания временных рядов является метод скользящих средних. Применяя этот метод, можно элиминировать случайные колебания и получить значения, соответствующие влиянию главных факторов. Сглаживание с помощью скользящих средних основано на том, что в средних величинах взаимно погашаются случайные отклонения. Это происходит вследствие замены первоначальных уровней временного ряда средней арифметической величиной внутри выбранного интервала времени. Полученное значение относится к середине выбранного периода. Затем период сдвигается на одно наблюдение, и расчет средней повторяется, причем периоды определения средней берутся все время одинаковыми. Таким образом, в каждом случае средняя центрирована, т.е. отнесена к серединной точке интервала сглаживания и представляет собой уровень для этой точки.
Данный метод используется при краткосрочном прогнозировании. Его рабочая формула:
 , если n
= 3 (1) , если n
= 3 (1)
гдеt
+ 1
– прогнозный период; t
– период, предшествующий прогнозному периоду (год, месяц и т.д.); yt
+1
– прогнозируемый показатель; – скользящая средняя за два периода до прогнозного; n
– число уровней, входящих в интервал сглаживания; yt
– фактическое значение исследуемого явления за предшествующий период; yt
-1
– фактическое значение исследуемого явления за два периода, предшествующих прогнозному. – скользящая средняя за два периода до прогнозного; n
– число уровней, входящих в интервал сглаживания; yt
– фактическое значение исследуемого явления за предшествующий период; yt
-1
– фактическое значение исследуемого явления за два периода, предшествующих прогнозному.
Для временного ряда показателя «Численность населения на 1 января» определим величину интервала сглаживания: n
=3. Исходные данные представлены в приложении 1. Рассчитаем скользящую среднюю для первых трех периодов:
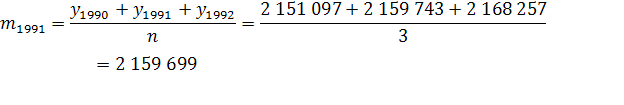
Далее рассчитываем скользящую среднюю для следующих трех периодов:
 и т.д. и т.д.
Составим таблицу расчетов (полностью в приложении 1).
Таблица 2
Расчет прогнозного значения численности населения в Оренбургской области методом скользящей средней.
| Годы |
Численность населения Оренбургской области на 1 января, человек |
Скользящая средняя m |
Расчет средней относительной ошибки
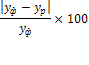
|
| 1990 |
2 151 097 |
- |
- |
| 1991 |
2 159 743 |
2 159 699 |
0,00 |
| 1992 |
2 168 257 |
2 170 201 |
0,09 |
| … |
| 2006 |
2 137 850 |
2 137 920 |
0,00 |
| 2007 |
2 125 503 |
2 127 452 |
0,09 |
| 2008 |
2 119 003 |
2 118 679 |
0,02 |
| 2009 |
2 111 531 |
2 115 267 |
- |
| итого |
43 528 625 |
0,85 |
| прогноз |
| 2010 |
2 116 188 |
2 114 949 |
| 2011 |
2 117 127 |
| 2012 |
2 115 261 |
| Средняя относительная ошибка ɛ |
0,05 |
Средняя абсолютная ошибка Δ
|
299 |
Средняя квадратическая ошибка 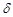 |
1 478 |
Рассчитав скользящую среднюю для всех периодов, построим прогноз на 2010 год по формуле (1):
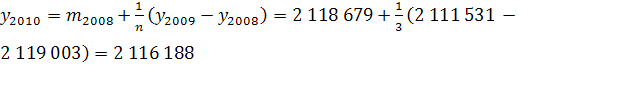
Определяем скользящую среднюю для 2009 года:
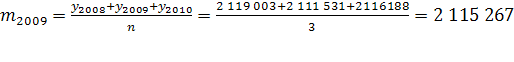 , ,
и строим прогноз на 2011 год:
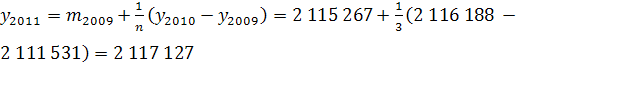 . .
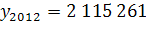 чел. чел.
В таблице 2 приведены расчетные данные для определения средней относительной ошибки. Найдем ее значение, разделив на число уровней (n
=18):
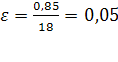 , что соответствует высокой точности прогноза. , что соответствует высокой точности прогноза.
Расчетные таблицы для определения прогнозных значений других демографических показателей приведены в приложении 1. Полученные результаты представим в таблице.
Таблица 3
Прогнозные значения абсолютных показателей родившихся, умерших, прибывших и выбывших в Оренбургской области, полученные методом скользящей средней.
| Абсолютный показатель, человек |
2006 |
2007 |
2008 |
Прогноз на 2009 |
Прогноз на 2010 |
Прогноз на 2011 |
Δ
|
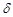 |
ε
|
| Родившиеся |
23335 |
25776 |
26947 |
25 743 |
25 754 |
26 125 |
-85 |
594 |
2,20 |
| Умершие |
31 583 |
31 000 |
30 904 |
31 130 |
31 087 |
31 026 |
32 |
795 |
2,02 |
| Абсолютный показатель, человек |
2007 |
2008 |
2009 |
Прогноз на 2010 |
Прогноз на 2011 |
Прогноз на 2012 |
Δ
|
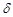 |
ε
|
| Прибывшие |
31 949 |
25 570 |
28 053 |
29 352 |
28 091 |
28 078 |
11 |
2177 |
5 |
| Выбывшие |
33 225 |
29 085 |
25 603 |
28 144 |
28 457 |
27 506 |
32 |
1161 |
2,05 |
Величины средних оценок и средней относительной ошибки позволяют считать точность прогноза достаточно высокой.
2.2 Нахождение прогнозных значений методом экспоненциального сглаживания
Метод экспоненциального сглаживания наиболее эффективен при разработке среднесрочных прогнозов. Он приемлем при прогнозировании только на один период вперед.
Рабочая формула метода экспоненциального сглаживания:
 (2) (2)
где t
– период, предшествующий прогнозному; t
+1
– прогнозный период; 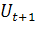 - прогнозируемый показатель; - прогнозируемый показатель;  - параметр сглаживания; - параметр сглаживания; 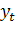 -фактическое значение исследуемого показателя за период, предшествующий прогнозному; -фактическое значение исследуемого показателя за период, предшествующий прогнозному; 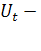 экспоненциально взвешенная средняя для периода, предшествующего прогнозному. экспоненциально взвешенная средняя для периода, предшествующего прогнозному.
При прогнозировании данным методом возникает два затруднения:
1) выбор значения параметра сглаживания α
;
2) определение начального значения U
о
.
От величины α
будет зависеть, как быстро снижается вес влияния предшествующих наблюдений. Чем больше α
, тем меньше сказывается влияние предшествующих лет. Если значение α
близко к единице, то это приводит к учету при прогнозе в основном влияния лишь последних наблюдений; если близко к нулю, то веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения. Таким образом, если есть уверенность, что начальные условия, на основании которых разрабатывается прогноз, достоверны, следует использовать небольшую величину параметра сглаживания (α→0). Когда параметр сглаживания мал, то исследуемая функция ведет себя как средняя из большого числа прошлых уровней. Если нет достаточной уверенности в начальных условиях прогнозирования, то следует использовать большую величину α, что приведет к учету при прогнозе в основном влияния последних наблюдений.
Точного метода для выбора оптимальной величины параметра сглаживания α
нет. В отдельных случаях автор данного метода профессор Браун предлагал определять величину α,
исходя из длины интервала сглаживания. При этом α
вычисляется по формуле:
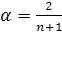 (3) (3)
где n
– число наблюдений, входящих в интервал сглаживания.
Задача выбора U
о
(экспоненциально взвешенного среднего начального) решается следующими путями:
1) если есть данные о развитии явления в прошлом, то можно воспользоваться средней арифметической, и U
о
равен этой средней арифметической;
2) если таких сведений нет, то в качестве U
о
используют исходное первое значение базы прогноза Y
1
.
Также можно воспользоваться экспертными оценками.
Используем метод экспоненциального сглаживания для составления прогнозных значений. Величина параметра сглаживания для показателя численности населения составит: 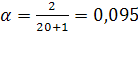 , для показателей «число родившихся» и «число умерших», «число прибывших» и «число выбывших»: , для показателей «число родившихся» и «число умерших», «число прибывших» и «число выбывших»:  . Значения близки к нулю, следовательно, веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения. . Значения близки к нулю, следовательно, веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения.
Определяем начальное значение U
о
для показателя численности населения двумя способами:
1 Способ (средняя арифметическая): 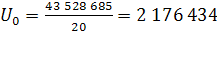
2 Способ (первое значение базы прогноза):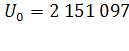
Рассчитываем экспоненциально взвешенную среднюю для каждого года, используя формулу 2, занесем результаты в таблицу.
Таблица 4
Расчет прогнозного значения численности населения Оренбургской области методом экпоненциального сглаживания.
| года |
Численность постоянного населения на 1 января, человек |
Экспоненциально взвешенная средняя Ut |
Расчет средней относительной ошибки
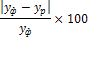
|
| I способ |
II способ |
I способ |
II способ |
| 1 |
1990 |
2 151 097 |
2176434 |
2 151 097 |
1,18 |
0,00 |
| 2 |
1991 |
2 159 743 |
2174021 |
2 151 097 |
0,66 |
0,40 |
| 3 |
1992 |
2 168 257 |
2172661 |
2 151 920 |
0,20 |
0,75 |
| … |
| 19 |
2008 |
2 119 003 |
2175920 |
2 171 738 |
2,69 |
2,49 |
| 20 |
2009 |
2 111 531 |
2170499 |
2 166 716 |
2,79 |
2,61 |
| прогноз |
2010 |
2 164 883 |
2 161 460 |
| итого |
43 528 685 |
27,20 |
29,84 |
| Средняя относительная ошибка ɛ |
1,36 |
1,49 |
Средняя абсолютная ошибка Δ
|
-6064 |
5441 |
Средняя квадратическая ошибка 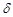 |
33749 |
36868 |
Величина средней относительной ошибки при расчете 2-м способом выше, но оба значения свидетельствуют о высокой точности прогноза.
Данные о прогнозных значениях показателей других демографических показателей, представим в таблице (расчет полученных параметров в Приложении 2).
Таблица 5
Прогнозные значения абсолютных показателей родившихся и умерших, прибывших и выбывших в Оренбургской области, полученные методом экспоненциального сглаживания.
| Абсолютный показатель, человек |
2006 |
2007 |
2008 |
Прогноз на 2009 |
Δ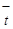
|
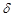 |
ε
|
| I способ определения экспоненциально взвешенного среднего начального |
| Родившиеся |
23 335 |
25 776 |
26 947 |
23 915 |
-135 |
3 275 |
9,94 |
| Умершие |
31 583 |
31 000 |
30 904 |
30 754 |
64 |
2 571 |
8,14 |
| II способ определения экспоненциально взвешенного среднего начального |
| Родившиеся |
23 335 |
25 776 |
26 947 |
25 150 |
-4296 |
5 386 |
20,14 |
| Умершие |
31 583 |
31 000 |
30 904 |
29 557 |
1 241 |
2 965 |
14,91 |
| I способ определения экспоненциально взвешенного среднего начального |
| Прибывшие |
31 949 |
25 570 |
28 053 |
37 366 |
-3539 |
15857 |
35,27 |
| Выбывшие |
33 225 |
29 085 |
25 603 |
36311 |
-2070 |
8458 |
20,04 |
| II способ определения экспоненциально взвешенного среднего начального |
| Прибывшие |
31 949 |
25 570 |
28 053 |
41 292 |
-16856 |
19228 |
49,84 |
| Выбывшие |
33 225 |
29 085 |
25 603 |
38 162 |
-8348 |
9757 |
24,83 |
Так же как и с показателем численности населения, величина средней относительной ошибки при расчете 2-м способом выше, что свидетельствует о нецелесообразности применения первого значения базы прогноза в качестве экспоненциально взвешенной U
о
.
В целом точность прогноза для показателей естественного движения населения находится в границах высокой точности, для показателей миграционного движения точность прогноза удовлетворительная.
2.3 Нахождение прогнозных значений методом наименьших квадратов
демографический прогноз население численность
Сущность метода наименьших квадратов состоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчетными величинами. Расчетные величины находятся по подобранному уравнению – уравнению регрессии.
Чем меньше расстояние между фактическими значениями и расчетными, тем более точен прогноз, построенный на основе уравнения регрессии. Теоретический анализ сущности изучаемого явления, изменение которого отображается временным рядом, служит основой для выбора кривой. Иногда принимаются во внимание соображения о характере роста уровней ряда. Для нахождения прогнозных значений численности населения часто предполагается, что рост идет в геометрической прогрессии, и тогда сглаживание производится по показательной функции.
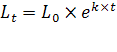 (4) (4)
где 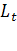 - численность населения в прогнозный период; - численность населения в прогнозный период; 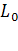 - численность населения в период, предшествующий прогнозному; е
- основные натурального логарифма; k
- общий коэффициент прироста населения, выраженный в долях единиц, рассчитанный по формуле: - численность населения в период, предшествующий прогнозному; е
- основные натурального логарифма; k
- общий коэффициент прироста населения, выраженный в долях единиц, рассчитанный по формуле: 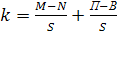 (5) (5)
где M
- число родившихся за период; N
– число умерших за период; П
- число прибывших за период; В
– число выбывших за период; S
– средняя численность населения за период; t- период, на который разрабатывается прогноз.
Согласно имеющимся данным, численность населения Оренбургской области на 1 января 2008 года составила 2 119 003 чел., на 1 января 2009 – 2 111 531 чел., за 2008 год родилось 26 947 чел., умерло 30 904 чел., 25 570 чел. прибыло и 29 085 чел. выбыло. Рассчитаем численность населения в 2010-2012 гг. при условии, что коэффициент общего прироста населения (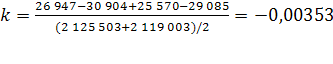 ) останется неизменным на всем протяжении прогнозных лет: ) останется неизменным на всем протяжении прогнозных лет:
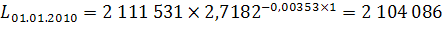 чел. чел.
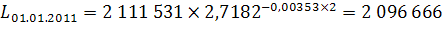 чел. чел.
 чел. чел.
Сглаживание временных рядов методом наименьших квадратов служит для отражения закономерности развития изучаемого явления. В аналитическом выражении тренда время рассматривается как независимая переменная, а уровни ряда выступают как функция этой независимой переменной. Ясно, что развитие явления зависит не от того, сколько лет прошло с отправного момента, а от того, какие факторы влияли на его развитие, в каком направлении и с какой интенсивностью. Развитие явления во времени выступает как результат действия этих факторов.
Правильно установить тип кривой, тип аналитической зависимости от времени – одна из самых трудных задач предпрогнозного анализа.
Подбор вида функции, описывающей тренд, параметры которой определяются методом наименьших квадратов, производится в большинстве случаев эмпирически, путем построения ряда функций и сравнения их между собой по величине среднеквадратической ошибки, вычисляемой по формуле:
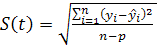 (6) (6)
где  – фактические значения ряда динамики; – фактические значения ряда динамики; – расчетные (сглаженные) значения ряда динамики; n
– число уровней временного ряда; р
– число параметров, определяемых в формулах, описывающих тренд. – расчетные (сглаженные) значения ряда динамики; n
– число уровней временного ряда; р
– число параметров, определяемых в формулах, описывающих тренд.
С помощью программы Excel проверим предположение о том, что изменение численности населения в Оренбургской области, хорошо апроксимируется экспоненциальной линией тренда.

Рис. 1. Динамика численности населения в Оренбургской области с экспоненциальной линией тренда.
Видно, что разница между фактическими и сглаженными значениями данного ряда очень велика. Невысокий коэффициент достоверности аппроксимации также подтверждает, что использовать данный тип тренда нецелесообразно.
Наибольшее приближение к фактическим уровням данного динамического ряда дает функция полинома второй степени.
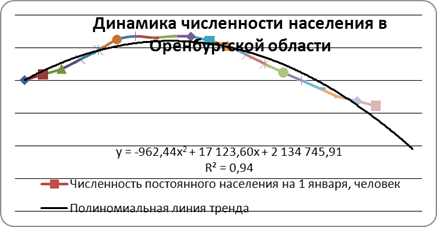
Рис. 2. Динамика численности населения в Оренбургской области с полиномиальной линией тренда.
При использовании уравнения полинома третьей степени, коэффициент аппроксимации увеличивается до 0,97, но при этом усложняется и сама модель, что может отрицательно сказаться на ее прогностических возможностях.
Уравнение регрессии примет вид:
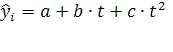 (7) (7)
 - выровненные, т.е. лишенные колебаний, уровни тренда для лет с номером i
; а -
это средний (выровненный) уровень тренда на момент или период, принятый за начало отсчета времени, т.е. t
=
0;
b
-
это средний за весь период среднегодовой прирост, который изменяется равномерно со средним ускорением, равным 2с; c
-
константа, главный параметр параболы II порядка. - выровненные, т.е. лишенные колебаний, уровни тренда для лет с номером i
; а -
это средний (выровненный) уровень тренда на момент или период, принятый за начало отсчета времени, т.е. t
=
0;
b
-
это средний за весь период среднегодовой прирост, который изменяется равномерно со средним ускорением, равным 2с; c
-
константа, главный параметр параболы II порядка.
Параметры a
,
b
и c
оцениваются методом наименьших квадратов и отвечают принципу максимального правдоподобия: сумма квадратов отклонений фактических уровней от тренда (от выровненных по уравнению тренда уровней) должна быть минимальной для данного типа уравнения.
На диаграмме уравнение тренда имеет вид: 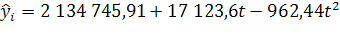 ,
где ,
где  =0 в 1990г. =0 в 1990г.
При этом нумерация периодов начинается с t
=1. Однако рациональнее начало отсчета времени перенести в середину ряда, т.е. при нечетном п -
на период (момент) с номером (п +
1 )/2, а при четном числе уровней ряда - на середину между периодом с номером n
/2
и (n/2)+1. Расчет параметров тренда при переносе отсчета времени на середину ряда приведен в приложении 3. Тогда уравнение тренда принимает вид: 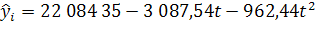 , где , где  =0,5 в 2000г. =0,5 в 2000г.
За период 1990-2009г показатель численности населения в Оренбургской области убывал в номинальной оценке ускоренно, со средним ускорением 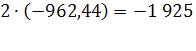 человек за год; средняя убыль населения за весь период составила 3 087 человек; средний уровень численности населения на середину периода был равен 22 084 35 чел. человек за год; средняя убыль населения за весь период составила 3 087 человек; средний уровень численности населения на середину периода был равен 22 084 35 чел.
Для оценки надежности тренда необходимо оценить надежность его главного параметра – ускорения. Средняя ошибка репрезентативности выборочной оценки параметра с
вычисляется по формуле:
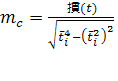 (8) (8)
Где S
(
t
)
– оценка генерального показателя колеблемости, учитывающая потерю степеней свободы и определяемая по формуле 6.
Используя данные приложения 3, найдем искомые величины:
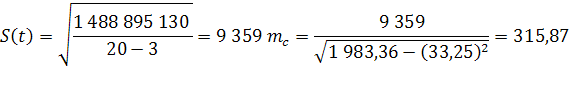
Отношение параметра с
(половина ускорения) к его средней ошибке - это t-критерий Стьюдента: 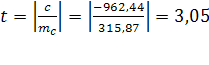
Табличное значение критерия Стъюдента 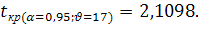 Фактическая величина критерия больше табличного, следовательно, вероятность нулевой гипотезы (о равенстве параметра с
нулю) чрезвычайно мала. Достоверно известно, что тренд существовал, и что численность населения Оренбургской области снижалась не случайно. Фактическая величина критерия больше табличного, следовательно, вероятность нулевой гипотезы (о равенстве параметра с
нулю) чрезвычайно мала. Достоверно известно, что тренд существовал, и что численность населения Оренбургской области снижалась не случайно.
Прогноз по этой модели заключается в подстановке в уравнение тренда номера периода, который прогнозируется. Для 2010 года период времени t
= 10,5, прогнозное значение составит:
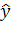 2010
= 2010
=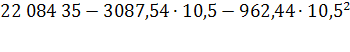 =2 069 907 чел. =2 069 907 чел.
Полученное прогнозное значение является точечным и не учитывает колеблемость уровней показателя.
При прогнозе с учетом случайной колеблемости учитывается как вызванная колеблемостью ошибка репрезентативности выборочной оценки тренда, так и колебания уровней в отдельные периоды (моменты) относительно тренда.
Общая формула средней ошибки прогноза положения параболического тренда на период с номером 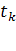 от середины базы расчета тренда имеет вид: от середины базы расчета тренда имеет вид:
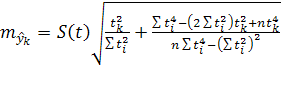 (9) (9)
Средняя ошибка тренда на 2010 год равна:
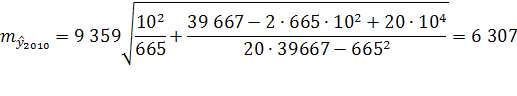
Вероятность того, что фактическая ошибка не превысит одного среднего квадратического отклонения, т.е. m
равна при нормальном распределении 0,68. Чтобы получить доверительный интервал прогноза линии тренда с большей вероятностью, например с вероятностью 0,95,среднюю ошибку нужно умножить на величину t-критерия Стъюдента для вероятности 0,95 и n
-
p
степеней свободы.
Получаем вероятную ошибку:
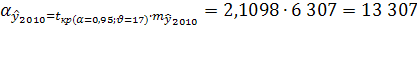
с вероятностью 95% можно утверждать, что тренд численности населения в Оренбургской области в 2010 году проходит в границах 2 069 907±13 307 или от 2 056 600 до 2 083 214 человек.
Определив ошибку репрезентативности выборочной оценки тренда, и колебания уровней в отдельные периоды (моменты) относительно тренда, получаем единую формулу средней ошибки прогноза конкретного отдельного уровня:
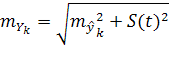 (10) (10)
Для искомого прогнозного значения: 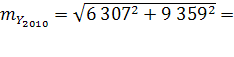 11 286 11 286  . .
Таким образом, для прогнозного значения показателя численности населения на 1 января 2010 года определены границы доверительного интервала 2 046 096 – 2 093 718 человек.
Аналогично рассчитываем прогнозные значения на 2011-2012 годы:
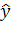 2011
=2 045 646 чел. 2011
=2 045 646 чел. 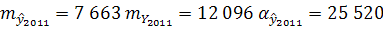
Доверительный интервал: (2 020 126; 2 071 166).
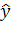 2012
=2 019 459 чел. 2012
=2 019 459 чел. 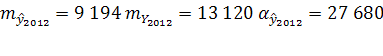
Доверительный интервал: (1 991 780; 2 047 138)
Средняя относительная ошибка 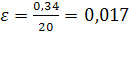 , что свидетельствует о высокой точности прогноза. , что свидетельствует о высокой точности прогноза.
Расчет прогнозных значений для других показателей приведен в приложении 3, сведем полученные результаты в общую таблицу:
Таблица 5
Прогнозные значения абсолютных показателей родившихся и умерших, прибывших и выбывших в Оренбургской области, полученные методом наименьших квадратов.
| Абсолютный показатель, человек |
2006 |
2007 |
2008 |
Прогноз на 2009 |
Прогноз на 2010 |
Прогноз на 2011 |
Δ
|
 |
ε
|
| Родившиеся |
23335 |
25776 |
26947 |
29 253 |
31 220 |
33 395 |
0 |
1135 |
4,13 |
| Умершие |
31 583 |
31 000 |
30 904 |
30 190 |
29 392 |
28 470 |
0 |
1420 |
3,69 |
| Абсолютный показатель, человек |
2007 |
2008 |
2009 |
Прогноз на 2010 |
Прогноз на 2011 |
Прогноз на 2012 |
Δ
|
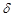 |
ε
|
| Прибывшие |
31 949 |
25 570 |
28 053 |
29 586 |
31 144 |
33 202 |
0,11 |
3499 |
7,68 |
| Выбывшие |
33 225 |
29 085 |
25 603 |
24 352 |
22 589 |
20 826 |
0 |
2437 |
5,17 |
Величины относительной ошибки свидетельствуют о высокой точности прогноза. По имеющимся данным видно, что при наметившихся тенденциях естественный прирост населения в прогнозируемые годы увеличится (увеличение рождаемости и снижение смертности), как и миграционный прирост.
Для сравнения полученных результатов составим сводную таблицу по всем применяемым методам:
| Численность постоянного населения на 1 января, человек |
| МСС |
МЭС |
МНК |
| 2007
|
2 125 503 |
2 125 503 |
2 125 503 |
| 2008
|
2 119 003 |
2 119 003 |
2 119 003 |
| 2009
|
2 111 531 |
2 111 531 |
2 111 531 |
| прогноз
|
| 2010
|
2 116 188 |
2 164 883 |
2 069 907 |
| 2011
|
2 117 127 |
2 045 646 |
| 2012
|
2 115 261 |
2 019 459 |
| Ср. абсолют. оценка |
299 |
-6064 |
0,38 |
| Ср. квадрат. оценка |
1 478 |
33749 |
8628 |
| Ср. относит. ошибка |
0,05 |
1,36 |
0,017 |
| Число родившихся, чел. |
Число умерших, чел. |
| МСС |
МЭС |
МНК |
МСС |
МЭС |
МНК |
| 2 006
|
23335 |
23335 |
23335 |
31 583 |
31 583 |
31 583 |
| 2 007
|
25776 |
25776 |
25776 |
31 000 |
31 000 |
31 000 |
| 2 008
|
26947 |
26947 |
26947 |
30 904 |
30 904 |
30 904 |
| прогноз
|
| 2 009
|
25 743 |
23 915 |
29 253 |
31 130 |
30 754 |
30 190 |
| 2 010
|
25 754 |
31 220 |
31 087 |
29 392 |
| 2 011
|
26 125 |
33 395 |
31 026 |
28 470 |
| Ср. абсолют. оценка |
-85 |
-135 |
0 |
32 |
64 |
0 |
| Ср. квадрат. оценка |
594 |
3 275 |
1135 |
795 |
2 571 |
1420 |
| Ср. относит. ошибка |
2 |
9,94 |
4,13 |
2,02 |
8,14 |
3,69 |
| Число прибывших, человек |
Число выбывших, человек |
| МСС |
МЭС |
МНК |
МСС |
МЭС |
МНК |
| 2007
|
31 949 |
31 949 |
31 949 |
33 225 |
33 225 |
33 225 |
| 2008
|
25 570 |
25 570 |
25 570 |
29 085 |
29 085 |
29 085 |
| 2009
|
28 053 |
28 053 |
28 053 |
25 603 |
25 603 |
25 603 |
| прогноз
|
| 2010
|
29 352 |
37 366 |
29 586 |
28 144 |
36311 |
24 352 |
| 2011
|
28 091 |
31 144 |
28 457 |
22 589 |
| 2012
|
28 078 |
33 202 |
27 506 |
20 826 |
| Ср. абсолют. оценка |
11 |
-3539 |
0,11 |
32 |
-2070 |
0 |
| Ср. квадрат. оценка |
2 177 |
15857 |
3499 |
1 161 |
8458 |
2437 |
| Ср. относит. ошибка |
5 |
35,27 |
7,68 |
2 |
20,04 |
5,17 |
Как видно из таблицы, значения средней квадратической оценки средней относительной ошибки у показателей минимальны для метода скользящей средней, и в целом данный метод дает хорошие результаты при прогнозировании демографических процессов. Кроме того, метод прост в использовании, что открывает широкие возможности для его применения. Метод наименьших квадратов более сложен в работе, но позволяет получить также достоверные результаты при условии подбора вида линии тренда, хорошо аппроксимирующей исходный динамический ряд.
Применение метода экспоненциального сглаживания целесообразно только при условии использования среднего уровня ряда в качестве начального значения экспоненциальной взвешенной. Но и в этом случае, полученные результаты являются самыми ненадежными по сравнению с прогнозированием другими методами.
Следует отметить, что прогнозирование методами экстраполяции основывается на использовании простого методологического аппарата и часто используется для получения будущих оценок социально-экономических процессов. Оправдано их использование и в частности при построении демографических прогнозов, поскольку процессы естественного и миграционного движения достаточно инерционны и не подвержены резким скачкам в уровнях.
Заключение
В соответствии с поставленными задачами в данной работе были исследованы 4 группы методов, используемых при прогнозировании демографических процессов:
1) методы экстраполяции;
2) экономико-математические методы, позволяющие разработать многофакторные динамические модели;
3) методы передвижки возрастов и когорт;
4) методы экспертных оценок.
Опираясь на имеющиеся в распоряжении данные, для практической части работы, была выбрана первая группа методов. В результате чего были построены прогнозные оценки показателей, характеризующих естественное и миграционное движения населения в Оренбургской области, с помощью трех методов экстраполяции:
- метод скользящей средней;
- метод экспоненциального сглаживания;
- метод наименьших квадратов.
Сравнив полученные результаты, сделаем вывод о целесообразности применения для прогнозирования метода скользящей средней и метода наименьших квадратов. Метод экспоненциального сглаживания позволил найти менее точные прогнозные оценки по сравнению с другими методами.
Метод наименьших квадратов позволил определить, что наилучшее приближение к исходным уровням временных рядов дает функция параболы II порядка для всех показателей, кроме «Числа выбывших, человек» - для него лучшей аппроксимацией является линейный тренд.
Для показателя «постоянного населения», «Число прибывших» и «Число выбывших» найдены прогнозные значения и определены границы доверительных интервалов на 2010, 2011,2012 годы.
Для показателей «Числа родившихся» и «Числа умерших» найдены прогнозные значения и определены границы доверительных интервалов на 2009, 2010,2011 годы.
Полученные абсолютные данные могут использоваться для формирования демографической политики, а также прогнозирования социально-экономических процессов.
Список использованных источников и литературы
1. Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование: Учебник. — М.: Финансы и статистика, 2001. — 228 с.
2. Артамонова И. А., Краснопевцева Б. В. Учебное пособие «Теория управления». Москва: МИИГАик, 2003.-86с.
3. Ахметов Р. Ш. Демографические процессы в Оренбургской области: вчера, сегодня, завтра – Региональный портал образовательного сообщества Оренбуржья http://www.orenport.ru/
4. Борисов В. А. Демография Учебник для вузов 2-е изд., исправленное— М.: Издательский дом NOTABENE, 1999, 2001. — 272 с.
5. Добров Г.М. Рабочая книга по прогнозированию. - М.: 1998
6. Концепция демографической политики Оренбургской области на период до 2025 года. Портал органов государственной власти Оренбуржья http://www.orenburggov.ru/magnoliaPublic/regportal/Info/SocialServices/dempolit/Main.html
7. Кузьмин А.И. Курс лекций "Основы демографии". Лекция 6 Основные показатели демографии. http://www.humanities.edu.ru/db/msg/47074
8. Курбатов В.И. Социальная работа: Учебное пособие. – М.: Издательско-торговая корпорация «Дашков и К», Ростов н/Д: Наука – Пресс, 2007 – 480с.
9. Луков В.А. Социальное проектирование. - М.: 1997. – 282 с.
10. Медков В. М. Демография: Учебное пособие. Серия «Учебники и учебные пособия». - Ростов-на-Дону: «Феникс», 2002. - 448 с.
11. Новикова Н.В., Поздеева О.Г. Прогнозирование национальной экономики: Учебно-методическое пособие. Екатеринбург: Изд-во Урал. гос. экон. ун-та, 2007. - с.138
12. Областной статистический ежегодник. 2009: Стат.сб./Территориальный орган Федеральной службы государственной статистики по Оренбургской области.- Оренбург. 2009. – 525 с.
13. Основы социальной работы: Учеб. пособие для студ. высш. учеб. заведений / Под ред. Н.Ф. Басова. – М.: Издательский центр «Академия», 2004. – 288 с.
14. Прогнозирование и планирование в условиях рынка./ Под редакцией Т.Г. Морозовой, А.В.Пулькина. М.: ЮНИТИ – ДИАНА, 20001 г., 318 с.
15. Сафронова В.М. Прогнозирование и моделирование в социальной работе: Учеб. пособие для студ. высш. учеб. заведений. – М.: Издательский центр «Академия», 2002. – 192с.
16. Смагина И. В. «Статистический анализ демографических процессов в Орловской области на фоне депопуляции населения России»: автореферат диссертации соискание ученой степени кандидата экономических наук www.econ.msu.ru/cmt2/lib/a/839/File/Smagina.doc
17. Смирнова И.В. Демография: Учебно-методическое пособие для студентов специальности «Государственное и муниципальное управление» / филиал СЗАГС в г. Калуга. – Калуга, 2004. – 138 с.
18. Теория управления. Учебник / Уколов В.Ф., Масс А.М., Быстряков И.К. - М.: Экономика, 2003. - 576 с.
19. Указ Президента РФ № 1351 от 9 октября 2007 года «Об утверждении Концепции демографической политики Российской Федерации на период до 2025 года»
20. Черныш Е.А., Молчанова и др. Прогнозирование и планирование. М., 2001 г.
21. Шмойлова Р.А, Минашкин В. Г. Теория статистики- Финансы и Статистика: 2009г., 656стр. Яковлева А.В. Эконометрика: конспект лекций ЭКсмо, 2008
22. Материалы сайтов www.demographia.ru, wikipedia.org.
Приложение 1
Расчет прогнозных значений абсолютного показателя родившихся методом скользящей средней.
| годы |
Число родившихся, человек |
Скользящая средняя m |
Расчет средней относительной ошибки
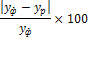
|
| итого |
37,38 |
| 1990 |
33 311 |
- |
- |
| 1991 |
30 177 |
30 327 |
0,50 |
| 1992 |
27 494 |
27 273 |
0,80 |
| 1993 |
24 148 |
25 367 |
5,05 |
| 1994 |
24 458 |
23 813 |
2,64 |
| 1995 |
22 833 |
22 913 |
0,35 |
| 1996 |
21 449 |
21 724 |
1,28 |
| 1997 |
20 890 |
21 430 |
2,58 |
| 1998 |
21 951 |
20 998 |
4,34 |
| 1999 |
20 154 |
21 193 |
5,16 |
| 2000 |
21 475 |
21 163 |
1,45 |
| 2001 |
21 861 |
22 279 |
1,91 |
| 2002 |
23 500 |
22 934 |
2,41 |
| 2003 |
23 442 |
23 508 |
0,28 |
| 2004 |
23 583 |
23 162 |
1,79 |
| 2005 |
22 460 |
23 126 |
2,97 |
| 2006 |
23 335 |
23 857 |
2,24 |
| 2007 |
25 776 |
25 353 |
1,64 |
| 2008 |
26 947 |
26 155 |
| прогноз 2009 |
25 743 |
26 148 |
| прогноз 2010 |
25 754 |
| прогноз 2011 |
26 125 |
| Средняя относительная ошибка |
2,20 |
| Средняя абсолютная ошибка |
-85 |
| Средняя квадратическая ошибка |
594 |
| Расчет прогнозных значений абсолютного показателя умерших методом скользящей средней. |
| итого |
22,64 |
| 1990 |
20 933 |
- |
| 1991 |
22 469 |
22 507 |
0,17 |
| 1992 |
24 120 |
24 991 |
3,61 |
| 1993 |
28 383 |
27 916 |
1,65 |
| 1994 |
31 244 |
29 887 |
4,34 |
| 1995 |
30 033 |
29 949 |
0,28 |
| 1996 |
28 570 |
28 938 |
1,29 |
| 1997 |
28 210 |
28 406 |
0,70 |
| 1998 |
28 439 |
29 006 |
1,99 |
| 1999 |
30 368 |
30 187 |
0,59 |
| 2000 |
31 755 |
31 472 |
0,89 |
| 2001 |
32 293 |
32 360 |
0,21 |
| 2002 |
33 031 |
32 772 |
0,79 |
| 2003 |
32 991 |
32 781 |
0,64 |
| 2004 |
32 321 |
32 819 |
1,54 |
| 2005 |
33 145 |
32 350 |
2,40 |
| 2006 |
31 583 |
31 909 |
1,03 |
| 2007 |
31 000 |
31 162 |
0,52 |
| 2008 |
30 904 |
31 011 |
| Прогноз 2009 |
31 130 |
31 040 |
| Прогноз 2010 |
31 087 |
| Прогноз 2011 |
31 026 |
| Средняя относительная ошибка |
2,02 |
| Средняя абсолютная ошибка |
32 |
| Средняя квадратическая ошибка |
795 |
Расчет прогнозных значений абсолютного показателя числа прибывших методом скользящей средней.
| годы |
Число прибывших за год |
Скользящая средняя m |
Расчет средней относительной ошибки
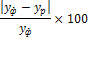
|
| итого |
75,0 |
| 1993 |
73131 |
| 1994 |
76108 |
73 160 |
3,87 |
| 1995 |
70242 |
68 229 |
2,87 |
| 1996 |
58336 |
62 100 |
6,45 |
| 1997 |
57721 |
55 832 |
3,27 |
| 1998 |
51438 |
52 475 |
2,02 |
| 1999 |
48267 |
47 730 |
1,11 |
| 2000 |
43484 |
41 538 |
4,47 |
| 2001 |
32864 |
35 192 |
7,08 |
| 2002 |
29228 |
30 611 |
4,73 |
| 2003 |
29740 |
29 556 |
0,62 |
| 2004 |
29701 |
30 921 |
4,11 |
| 2005 |
33322 |
30 912 |
7,23 |
| 2006 |
29712 |
31 661 |
6,56 |
| 2007 |
31949 |
29 077 |
8,99 |
| 2008 |
25570 |
28 524 |
11,55 |
| 2009 |
28 053 |
27 658 |
1,41 |
| Прогноз 2010 |
29 352 |
28 499 |
| Прогноз 2011 |
28 091 |
| Прогноз 2012 |
28 078 |
| Средняя относительная ошибка |
5 |
| Средняя абсолютная ошибка |
11 |
| Средняя квадратическая ошибка |
2 177 |
Расчет прогнозных значений абсолютного показателя числа выбывших методом скользящей средней.
| годы |
Число выбывших за год |
Скользящая средняя m |
Расчет средней относительной ошибки
|
| итого |
31,0 |
| 1993 |
53931 |
| 1994 |
51900 |
54 083 |
4,21 |
| 1995 |
56419 |
53 455 |
5,25 |
| 1996 |
52047 |
51 873 |
0,33 |
| 1997 |
47152 |
47 831 |
1,44 |
| 1998 |
44293 |
45 041 |
1,69 |
| 1999 |
43678 |
42 558 |
2,56 |
| 2000 |
39703 |
39 702 |
0,00 |
| 2001 |
35725 |
36 248 |
1,46 |
| 2002 |
33317 |
34 516 |
3,60 |
| 2003 |
34506 |
33 952 |
1,61 |
| 2004 |
34032 |
34 577 |
1,60 |
| 2005 |
35194 |
34 389 |
2,29 |
| 2006 |
33940 |
34 120 |
0,53 |
| 2007 |
33225 |
32 083 |
3,44 |
| 2008 |
29085 |
29 304 |
0,75 |
| 2009 |
25 603 |
27 611 |
| Прогноз 2010 |
28 144 |
27 401 |
| Прогноз 2011 |
28 457 |
| Прогноз 2012 |
27 506 |
| Средняя относительная ошибка |
2,05 |
| Средняя абсолютная ошибка |
32 |
| Средняя квадратическая ошибка |
1 161 |
Приложение 2
Расчет прогнозного значения абсолютного показателя родившихся в Оренбургской области методом экпоненциального сглаживания.
| года |
Число родившихся, человек |
Экспоненциально взвешенная средняя Ut
|
Расчет средней относительной ошибки
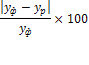
|
| Iспособ |
IIспособ |
I способ |
II способ |
| 1 |
1990 |
33311 |
24 171 |
33 311 |
27,44 |
0,00 |
| 2 |
1991 |
30177 |
25 085 |
33 311 |
16,87 |
10,39 |
| 3 |
1992 |
27494 |
25 594 |
32 998 |
6,91 |
20,02 |
| 4 |
1993 |
24148 |
25 784 |
32 447 |
6,77 |
34,37 |
| 5 |
1994 |
24458 |
25 620 |
31 617 |
4,75 |
29,27 |
| 6 |
1995 |
22833 |
25 504 |
30 901 |
11,70 |
35,34 |
| 7 |
1996 |
21449 |
25 237 |
30 095 |
17,66 |
40,31 |
| 8 |
1997 |
20890 |
24 858 |
29 230 |
19,00 |
39,92 |
| 9 |
1998 |
21951 |
24 461 |
28 396 |
11,44 |
29,36 |
| 10 |
1999 |
20154 |
24 210 |
27 751 |
20,13 |
37,70 |
| 11 |
2000 |
21475 |
23 805 |
26 992 |
10,85 |
25,69 |
| 12 |
2001 |
21861 |
23 572 |
26 440 |
7,83 |
20,95 |
| 13 |
2002 |
23500 |
23 401 |
25 982 |
0,42 |
10,56 |
| 14 |
2003 |
23442 |
23 411 |
25 734 |
0,13 |
9,78 |
| 15 |
2004 |
23583 |
23 414 |
25 505 |
0,72 |
8,15 |
| 16 |
2005 |
22460 |
23 431 |
25 313 |
4,32 |
12,70 |
| 17 |
2006 |
23335 |
23 334 |
25 027 |
0,01 |
7,25 |
| 18 |
2007 |
25776 |
23 334 |
24 858 |
9,47 |
3,56 |
| 19 |
2008 |
26947 |
23 578 |
24 950 |
12,50 |
7,41 |
| прогноз |
2009 |
23 915 |
25 150 |
| итого |
459 244 |
188,92 |
382,72 |
| Средняя относительная ошибка ɛ |
9,94 |
20,14 |
Средняя абсолютная ошибка Δ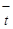
|
-135 |
-4 296 |
Средняя квадратическая ошибка 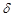 |
3 275 |
5 386 |
Расчет прогнозного значения абсолютного показателя умерших в Оренбургской области методом экпоненциального сглаживания.
| года |
Число умерших, человек |
Экспоненциально взвешенная средняя Ut
|
Расчет средней относительной ошибки
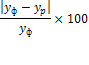
|
| Iспособ |
IIспособ |
I способ |
II способ |
| 1 |
1990 |
20933 |
29 795 |
20 933 |
2,34 |
0,00 |
| 2 |
1991 |
22469 |
28 909 |
20 933 |
28,66 |
6,84 |
| 3 |
1992 |
28 439 |
28 265 |
21 087 |
0,61 |
25,85 |
| 4 |
1993 |
28383 |
28 282 |
21 822 |
0,35 |
23,12 |
| 5 |
1994 |
31244 |
28 293 |
22 478 |
9,45 |
28,06 |
| 6 |
1995 |
30033 |
28 588 |
23 355 |
4,81 |
22,24 |
| 7 |
1996 |
28570 |
28 732 |
24 022 |
0,57 |
15,92 |
| 8 |
1997 |
28210 |
28 716 |
24 477 |
1,79 |
13,23 |
| 9 |
1998 |
28439 |
28 665 |
24 850 |
0,80 |
12,62 |
| 10 |
1999 |
30368 |
28 643 |
25 209 |
5,68 |
16,99 |
| 11 |
2000 |
31755 |
28 815 |
25 725 |
9,26 |
18,99 |
| 12 |
2001 |
32293 |
29 109 |
26 328 |
9,86 |
18,47 |
| 13 |
2002 |
33031 |
29 428 |
26 925 |
10,91 |
18,49 |
| 14 |
2003 |
32991 |
29 788 |
27 535 |
9,71 |
16,54 |
| 15 |
2004 |
32321 |
30 108 |
28 081 |
6,85 |
13,12 |
| 16 |
2005 |
33145 |
30 330 |
28 505 |
8,49 |
14,00 |
| 17 |
2006 |
31583 |
30 611 |
28 969 |
3,08 |
8,28 |
| 18 |
2007 |
31000 |
30 708 |
29 230 |
0,94 |
5,71 |
| 19 |
2008 |
30904 |
30 737 |
29 407 |
0,54 |
4,84 |
| прогноз |
2009 |
30 754 |
29 557 |
| итого |
566 111 |
154,69 |
283,29 |
| Средняя относительная ошибка ɛ |
8,14 |
14,91 |
Средняя абсолютная ошибка Δ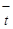
|
64 |
1241 |
Средняя квадратическая ошибка 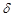 |
2 571 |
2 965 |
Расчет прогнозного значения абсолютного показателя прибывших в Оренбургской области методом экпоненциального сглаживания.
| года |
Число прибывших, человек |
Экспоненциально взвешенная средняя Ut
|
Расчет средней относительной ошибки
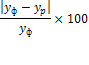
|
| Iспособ |
IIспособ |
I способ |
II способ |
| 1 |
1993 |
73131 |
44 051 |
73 131 |
39,76 |
0,00 |
| 2 |
1994 |
76108 |
47 282 |
73 131 |
37,88 |
3,91 |
| 3 |
1995 |
70242 |
50 485 |
73 462 |
28,13 |
4,58 |
| 4 |
1996 |
58336 |
52 680 |
73 104 |
9,70 |
25,32 |
| 5 |
1997 |
57721 |
53 309 |
71 463 |
7,64 |
23,81 |
| 6 |
1998 |
51438 |
53 799 |
69 936 |
4,59 |
35,96 |
| 7 |
1999 |
48267 |
53 537 |
67 881 |
10,92 |
40,64 |
| 8 |
2000 |
43484 |
52 951 |
65 702 |
21,77 |
51,09 |
| 9 |
2001 |
32864 |
51 899 |
63 233 |
57,92 |
92,41 |
| 10 |
2002 |
29228 |
49 784 |
59 859 |
70,33 |
104,80 |
| 11 |
2003 |
29740 |
47 500 |
56 455 |
59,72 |
89,83 |
| 12 |
2004 |
29701 |
45 527 |
53 487 |
53,28 |
80,08 |
| 13 |
2005 |
33322 |
43 768 |
50 844 |
31,35 |
52,58 |
| 14 |
2006 |
29712 |
42 608 |
48 897 |
43,40 |
64,57 |
| 15 |
2007 |
31949 |
41 175 |
46 765 |
28,88 |
46,38 |
| 16 |
2008 |
25570 |
40 150 |
45 119 |
57,02 |
76,45 |
| 17 |
2009 |
28053 |
38 530 |
42 947 |
37,35 |
53,09 |
| прогноз |
2010 |
37 366 |
41 292 |
| итого |
748866 |
599,6 |
845,51 |
| Средняя относительная ошибка ɛ |
35,27 |
49,74 |
Средняя абсолютная ошибка Δ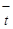
|
-3 539 |
-16 856 |
Средняя квадратическая ошибка 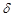 |
15 857 |
19 228 |
Расчет прогнозного значения абсолютного показателя выбывших в Оренбургской области методом экпоненциального сглаживания.
| года |
Число выбывших, человек |
Экспоненциально взвешенная средняя Ut
|
Расчет средней относительной ошибки
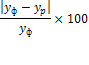
|
| Iспособ |
IIспособ |
I способ |
II способ |
| 1 |
1993 |
53931 |
40 221 |
53 931 |
25,42 |
0,00 |
| 2 |
1994 |
51900 |
41 744 |
53 931 |
19,57 |
3,91 |
| 3 |
1995 |
56419 |
42 872 |
53 705 |
24,01 |
4,81 |
| 4 |
1996 |
52047 |
44 378 |
54 007 |
14,74 |
3,77 |
| 5 |
1997 |
47152 |
45 230 |
53 789 |
4,08 |
14,08 |
| 6 |
1998 |
44293 |
45 443 |
53 052 |
2,60 |
19,77 |
| 7 |
1999 |
43678 |
45 316 |
52 078 |
3,75 |
19,23 |
| 8 |
2000 |
39703 |
45 134 |
51 145 |
13,68 |
28,82 |
| 9 |
2001 |
35725 |
44 530 |
49 874 |
24,65 |
39,60 |
| 10 |
2002 |
33317 |
43 552 |
48 302 |
30,72 |
44,98 |
| 11 |
2003 |
34506 |
42 415 |
46 637 |
22,92 |
35,16 |
| 12 |
2004 |
34032 |
41 536 |
45 289 |
22,05 |
33,08 |
| 13 |
2005 |
35194 |
40 702 |
44 038 |
15,65 |
25,13 |
| 14 |
2006 |
33940 |
40 090 |
43 055 |
18,12 |
26,86 |
| 15 |
2007 |
33225 |
39 407 |
42 043 |
18,61 |
26,54 |
| 16 |
2008 |
29085 |
38 720 |
41 063 |
33,13 |
41,18 |
| 17 |
2009 |
25603 |
37 649 |
39 732 |
47,05 |
55,18 |
| прогноз |
2010 |
36 311 |
38 162 |
| итого |
683750 |
340,73 |
422,10 |
| Средняя относительная ошибка ɛ |
20,04 |
24,83 |
Средняя абсолютная ошибка Δ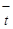
|
-2070 |
-8348 |
Средняя квадратическая ошибка 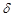 |
8458 |
9757 |
Приложение 3
Расчет параметров параболического тренда для абсолютного показателя численности населения в Оренбургской области.
| годы |
Численность населения, человек  |
Условное обозначение времениt
|
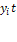 |
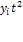 |
Тренд  |
| 1990 |
2 151 097 |
-9,5 |
-20 435 422 |
194 136 504 |
2 150 906 |
| 1991 |
2 159 743 |
-8,5 |
-18 357 816 |
156 041 432 |
2 165 143 |
| 1992 |
2 168 257 |
-7,5 |
-16 261 928 |
121 964 456 |
2 177 454 |
| 1993 |
2 182 602 |
-6,5 |
-14 186 913 |
92 214 935 |
2 187 841 |
| 1994 |
2 196 785 |
-5,5 |
-12 082 318 |
66 452 746 |
2 196 303 |
| 1995 |
2 213 038 |
-4,5 |
-9 958 671 |
44 814 020 |
2 202 840 |
| 1996 |
2 218 052 |
-3,5 |
-7 763 182 |
27 171 137 |
2 207 452 |
| 1997 |
2 215 936 |
-2,5 |
-5 539 840 |
13 849 600 |
2 210 139 |
| 1998 |
2 218 082 |
-1,5 |
-3 327 123 |
4 990 685 |
2 210 901 |
| 1999 |
2 217 558 |
-0,5 |
-1 108 779 |
554 390 |
2 209 738 |
| 2000 |
2 211 204 |
0,5 |
1 105 602 |
552 801 |
2 206 651 |
| 2001 |
2 203 616 |
1,5 |
3 305 424 |
4 958 136 |
2 201 638 |
| 2002 |
2 189 876 |
2,5 |
5 474 690 |
13 686 725 |
2 194 701 |
| 2003 |
2 176 000 |
3,5 |
7 616 000 |
26 656 000 |
2 185 839 |
| 2004 |
2 162 545 |
4,5 |
9 731 453 |
43 791 536 |
2 175 052 |
| 2005 |
2 150 407 |
5,5 |
11 827 239 |
65 049 812 |
2 162 340 |
| 2006 |
2 137 850 |
6,5 |
13 896 025 |
90 324 163 |
2 147 703 |
| 2007 |
2 125 503 |
7,5 |
15 941 273 |
119 559 544 |
2 131 141 |
| 2008 |
2 119 003 |
8,5 |
18 011 526 |
153 097 967 |
2 112 655 |
| 2009 |
2 111 531 |
9,5 |
20 059 545 |
190 565 673 |
2 092 243 |
| Итого
|
43 528 685 |
0
|
-2 053 216 |
1 430 432 259 |
2 150 906 |
Три частные производные функции: 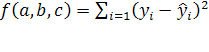 приравниваются к нулю, и после преобразований получаем систему трех уравнений с тремя неизвестными: приравниваются к нулю, и после преобразований получаем систему трех уравнений с тремя неизвестными:
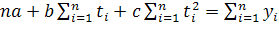 (11) (11)
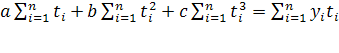 (12) (12)
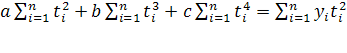 (13) (13)
При переносе начала отсчета периодов (моментов) времени в середину ряда суммы нечетных степеней номеров этих периодов 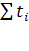 и и 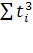 обращаются в нуль. При этом второе уравнение обращается в уравнение с одним неизвестным, откуда: обращаются в нуль. При этом второе уравнение обращается в уравнение с одним неизвестным, откуда: 
Уравнения (11) и (13) образуют систему двух уравнений с двумя неизвестными:
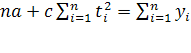 (14) (14)
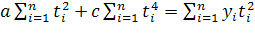 (15) (15)
Где 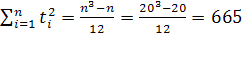 ; ; 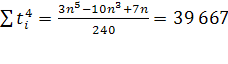
По данным таблицы вычисляем параметры:


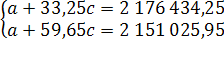
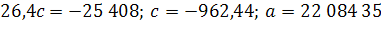
Расчет прогнозных значений показателя численности населения в Оренбургской области, величин средней относительной ошибки ɛ, среднего квадратического отклонения уровней ряда от тренда S(t).
| годы |
Числен-ность населения, человек  |
Условное обозна-
чение времениt
|
 |
 |
Тренд

|
Расчет средней относительной ошибки
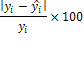
|
 |
| 1990 |
2 151 097 |
-9,5 |
90,25 |
8 145,06 |
2 150 906 |
0,01 |
36 313,11 |
| 1991 |
2 159 743 |
-8,5 |
72,25 |
5 220,06 |
2 165 143 |
0,25 |
29 158 033,30 |
| 1992 |
2 168 257 |
-7,5 |
56,25 |
3 164,06 |
2 177 454 |
0,42 |
84 590 617,73 |
| 1993 |
2 182 602 |
-6,5 |
42,25 |
1 785,06 |
2 187 841 |
0,24 |
27 446 426,15 |
| 1994 |
2 196 785 |
-5,5 |
30,25 |
915,06 |
2 196 303 |
0,02 |
232 640,71 |
| 1995 |
2 213 038 |
-4,5 |
20,25 |
410,06 |
2 202 840 |
0,46 |
104 008 801,08 |
| 1996 |
2 218 052 |
-3,5 |
12,25 |
150,06 |
2 207 452 |
0,48 |
112 370 444,03 |
| 1997 |
2 215 936 |
-2,5 |
6,25 |
39,06 |
2 210 139 |
0,26 |
33 609 785,73 |
| 1998 |
2 218 082 |
-1,5 |
2,25 |
5,06 |
2 210 901 |
0,32 |
51 569 300,84 |
| 1999 |
2 217 558 |
-0,5 |
0,25 |
0,06 |
2 209 738 |
0,35 |
61 149 881,16 |
| 2000 |
2 211 204 |
0,5 |
0,25 |
0,06 |
2 206 651 |
0,21 |
20 733 279,01 |
| 2001 |
2 203 616 |
1,5 |
2,25 |
5,06 |
2 201 638 |
0,09 |
3 911 705,33 |
| 2002 |
2 189 876 |
2,5 |
6,25 |
39,06 |
2 194 701 |
0,22 |
23 279 609,22 |
| 2003 |
2 176 000 |
3,5 |
12,25 |
150,06 |
2 185 839 |
0,45 |
96 800 266,25 |
| 2004 |
2 162 545 |
4,5 |
20,25 |
410,06 |
2 175 052 |
0,58 |
156 416 307,39 |
| 2005 |
2 150 407 |
5,5 |
30,25 |
915,06 |
2 162 340 |
0,55 |
142 389 530,26 |
| 2006 |
2 137 850 |
6,5 |
42,25 |
1 785,06 |
2 147 703 |
0,46 |
97 079 368,75 |
| 2007 |
2 125 503 |
7,5 |
56,25 |
3 164,06 |
2 131 141 |
0,27 |
31 789 121,19 |
| 2008 |
2 119 003 |
8,5 |
72,25 |
5 220,06 |
2 112 655 |
0,30 |
40 302 155,83 |
| 2009 |
2 111 531 |
9,5 |
90,25 |
8 145,06 |
2 092 243 |
0,91 |
372 021 543,38 |
| Итого
|
43 528 685
|
0
|
665
|
39 667
|
2 150 906
|
0,34
|
1 488 895 130
|
| Ср.зн.
|
2 176 434
|
33,25
|
1 983,36
|
Для показателя числа родившихся функцией тренда лучше всего аппроксимирующей временной ряд также является парабола II порядка:
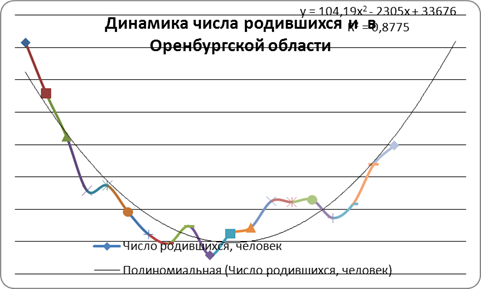
Рис. 3. Динамика числа родившихся в Оренбургской области с полиномиальной линией тренда.
Расчет параметров параболического тренда для абсолютного показателя числа родившихся в Оренбургской области.
 ; ; 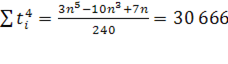
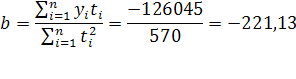
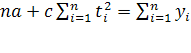 
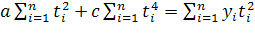 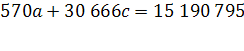
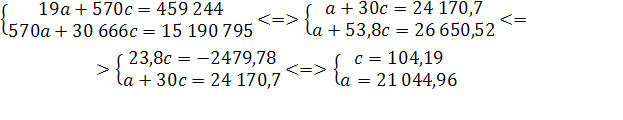
Уравнение регрессии:
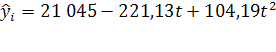 , где , где  =0 в 1999г. =0 в 1999г.
Среднее квадратическое отклонение:
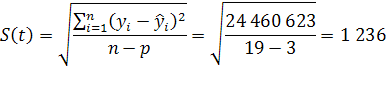
Средняя ошибка репрезентативности выборочной оценки параметра с:
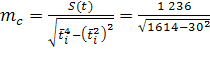 =46,27 =46,27
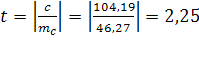 
Фактическая величина t-критерия  больше табличного больше табличного 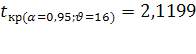 , следовательно, вероятность нулевой гипотезы (о равенстве параметра с
нулю) чрезвычайно мала. Достоверно известно, что тренд существовал, и что численность числа родившихся в Оренбургской области снижалась не случайно. , следовательно, вероятность нулевой гипотезы (о равенстве параметра с
нулю) чрезвычайно мала. Достоверно известно, что тренд существовал, и что численность числа родившихся в Оренбургской области снижалась не случайно.
Средняя ошибка прогноза положения параболического тренда на период с номером 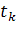 : :
 =949 =949
 =1 156 =1 156
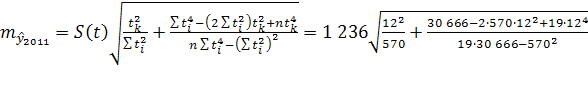 =1 390 =1 390
Средняя ошибка прогноза:
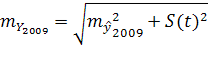 = =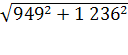 = 1 558 = 1 558
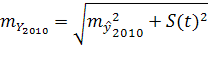 = =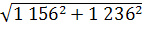 = 1 693 = 1 693
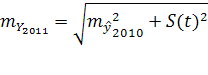 = =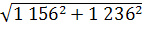 = 1 860 = 1 860
Вероятная ошибка прогноза:
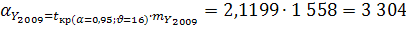

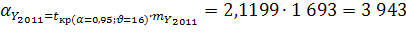
Прогнозные значения:
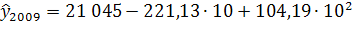 =29 253 =29 253
Доверительный интервал (25 949; 32 557)
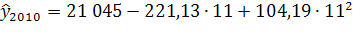 =31 220 =31 220
Доверительный интервал (27 630; 34 809)
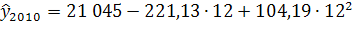 =33 395 =33 395
Доверительный интервал (29 452; 37 338)
Как видно по полученным данным, при сохранении имеющейся тенденции, число родившихся продолжит расти и вероятно в 2011 году превысит максимальный уровень в наблюдаемом периоде (1990г.)
Средняя относительная ошибка:
 прогноз обладает высокой точностью. прогноз обладает высокой точностью.
| годы |
Число родив-шихся, человек  |
Условное обозначение времениt
|
 |
 |
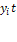 |
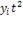 |
Тренд  |
Расчет средней относительной ошибки
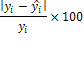
|
 |
| 1990
|
33 311 |
-9 |
81 |
6561 |
-299799 |
2698191 |
31 474,74 |
5,51 |
3 371 862,39 |
| 1991
|
30 177 |
-8 |
64 |
4096 |
-241416 |
1931328 |
29 482,33 |
2,30 |
482 561,78 |
| 1992
|
27 494 |
-7 |
49 |
2401 |
-192458 |
1347206 |
27 698,31 |
0,74 |
41 744,52 |
| 1993
|
24 148 |
-6 |
36 |
1296 |
-144888 |
869328 |
26 122,68 |
8,18 |
3 899 365,50 |
| 1994
|
24 458 |
-5 |
25 |
625 |
-122290 |
611450 |
24 755,43 |
1,22 |
88 466,04 |
| 1995
|
22 833 |
-4 |
16 |
256 |
-91332 |
365328 |
23 596,57 |
3,34 |
583 037,05 |
| 1996
|
21 449 |
-3 |
9 |
81 |
-64347 |
193041 |
22 646,09 |
5,58 |
1 433 023,95 |
| 1997
|
20 890 |
-2 |
4 |
16 |
-41780 |
83560 |
21 904,00 |
4,85 |
1 028 187,63 |
| 1998
|
21 951 |
-1 |
1 |
1 |
-21951 |
21951 |
21 370,29 |
2,65 |
337 227,71 |
| 1999
|
20 154 |
0 |
0 |
0 |
0 |
0 |
21 044,96 |
4,42 |
793 814,80 |
| 2000
|
21 475 |
1 |
1 |
1 |
21475 |
21475 |
20 928,02 |
2,55 |
299 183,03 |
| 2001
|
21 861 |
2 |
4 |
16 |
43722 |
87444 |
21 019,47 |
3,85 |
708 173,49 |
| 2002
|
23 500 |
3 |
9 |
81 |
70500 |
211500 |
21 319,30 |
9,28 |
4 755 451,14 |
| 2003
|
23 442 |
4 |
16 |
256 |
93768 |
375072 |
21 827,52 |
6,89 |
2 606 558,60 |
| 2004
|
23 583 |
5 |
25 |
625 |
117915 |
589575 |
22 544,12 |
4,41 |
1 079 278,69 |
| 2005
|
22 460 |
6 |
36 |
1296 |
134760 |
808560 |
23 469,10 |
4,49 |
1 018 287,18 |
| 2006
|
23 335 |
7 |
49 |
2401 |
163345 |
1143415 |
24 602,47 |
5,43 |
1 606 486,92 |
| 2007
|
25 776 |
8 |
64 |
4096 |
206208 |
1649664 |
25 944,23 |
0,65 |
28 300,68 |
| 2008
|
26 947 |
9 |
81 |
6561 |
242523 |
2182707 |
27 494,37 |
2,03 |
299 612,19 |
| Итого |
459 244
|
0
|
570
|
30 666
|
-126 045
|
15 190 795
|
459 244,00
|
78,37
|
24 460 623
|
| Ср. Знач. |
30
|
1614
|
Расчет параметров параболического тренда для абсолютного показателя числа умерших в Оренбургской области.
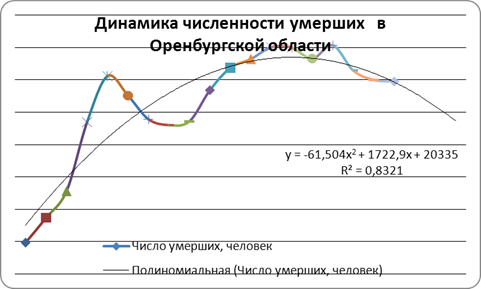
Рис. 4. Динамика числа умерших в Оренбургской области с полиномиальной линией тренда.
 ; ; 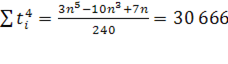
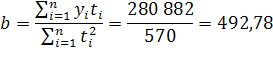
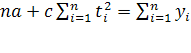 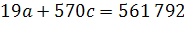
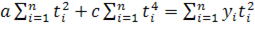 
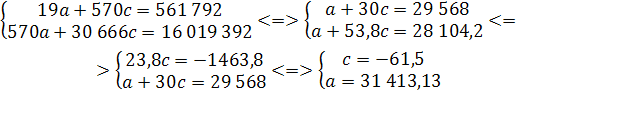
Уравнение регрессии:
 , где , где  =0 в 1999г. =0 в 1999г.
Среднее квадратическое отклонение:
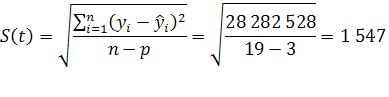
Средняя ошибка прогноза положения параболического тренда на период с номером 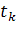 : :
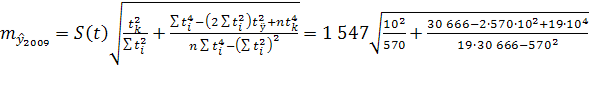 =1 187 =1 187
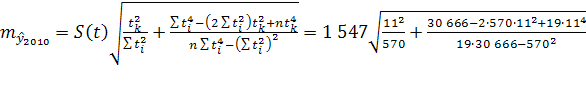 =1 447 =1 447
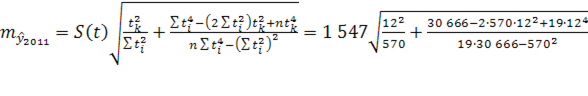 =1 739 =1 739
Средняя ошибка прогноза:
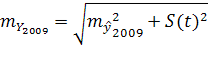 = = = 1 950 = 1 950
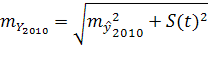 = = = 2 118 = 2 118
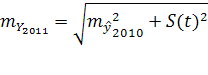 = = = 2 327 = 2 327
Вероятная ошибка прогноза:
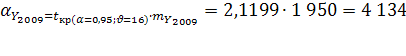
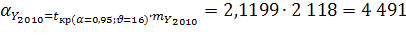
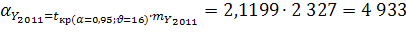
Прогнозные значения:
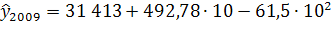 =30 190 =30 190
Доверительный интервал (26 057; 34 324)
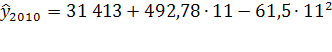 =29 392 =29 392
Доверительный интервал (25 258; 33 525)
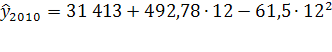 =28 470 =28 470
Доверительный интервал (24 336; 32 604)
При сохранении имеющейся тенденции, число умерших будет снижаться.
Средняя относительная ошибка:

прогноз обладает высокой точностью.
| годы |
Число умерших, человек  |
Условное обозначение времениt
|
 |
 |
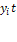 |
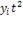 |
Тренд  |
Расчет средней относительной ошибки
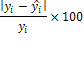
|
 |
| 1990 |
20 933 |
-9 |
81 |
6561 |
-188397 |
1695573 |
-332 202 |
5,08 |
1 130 605,29 |
| 1991 |
22 469 |
-8 |
64 |
4096 |
-179752 |
1438016 |
-188 971 |
4,74 |
1 135 606,98 |
| 1992 |
24 120 |
-7 |
49 |
2401 |
-168840 |
1181880 |
-92 113 |
3,44 |
688 882,23 |
| 1993 |
28 383 |
-6 |
36 |
1296 |
-170298 |
1021788 |
-30 557 |
7,54 |
4 582 505,41 |
| 1994 |
31 244 |
-5 |
25 |
625 |
-156220 |
781100 |
5 292 |
12,27 |
14 686 948,28 |
| 1995 |
30 033 |
-4 |
16 |
256 |
-120132 |
480528 |
23 552 |
5,24 |
2 480 753,73 |
| 1996 |
28 570 |
-3 |
9 |
81 |
-85710 |
257130 |
30 866 |
2,84 |
658 150,93 |
| 1997 |
28 210 |
-2 |
4 |
16 |
-56420 |
112840 |
32 400 |
6,99 |
3 887 057,51 |
| 1998 |
28 439 |
-1 |
1 |
1 |
-28439 |
28439 |
31 844 |
8,51 |
5 855 677,34 |
| 1999 |
30 368 |
0 |
0 |
0 |
0 |
0 |
31 413 |
3,44 |
1 092 297,71 |
| 2000 |
31 755 |
1 |
1 |
1 |
31755 |
31755 |
31 844 |
0,28 |
7 992,64 |
| 2001 |
32 293 |
2 |
4 |
16 |
64586 |
129172 |
32 400 |
0,43 |
19 694,21 |
| 2002 |
33 031 |
3 |
9 |
81 |
99093 |
297279 |
30 866 |
2,10 |
480 363,15 |
| 2003 |
32 991 |
4 |
16 |
256 |
131964 |
527856 |
23 552 |
1,79 |
349 088,78 |
| 2004 |
32 321 |
5 |
25 |
625 |
161605 |
808025 |
5 292 |
0,06 |
338,52 |
| 2005 |
33 145 |
6 |
36 |
1296 |
198870 |
1193220 |
-30 557 |
2,98 |
978 859,85 |
| 2006 |
31 583 |
7 |
49 |
2401 |
221081 |
1547567 |
-92 113 |
0,84 |
70 673,80 |
| 2007 |
31 000 |
8 |
64 |
4096 |
248000 |
1984000 |
-188 971 |
1,35 |
175 607,63 |
| 2008 |
30 904 |
9 |
81 |
6561 |
278136 |
2503224 |
-332 202 |
0,12 |
1 424,52 |
| Итого |
561 792
|
0
|
570
|
30 666
|
280 882
|
16 019 392
|
-1 008 361
|
70
|
38 282 528
|
| Ср. Знач. |
30 |
1614 |
Расчет параметров параболического тренда для абсолютного показателя числа прибывших в Оренбургской области.
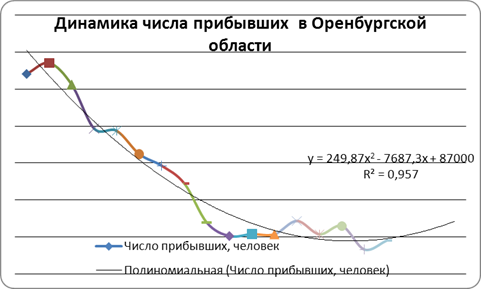
Рис. 5. Динамика числа прибывших в Оренбургской области с полиномиальной линией тренда.
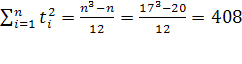 ; ; 
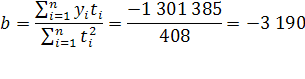
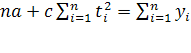 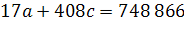
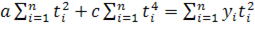 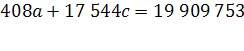
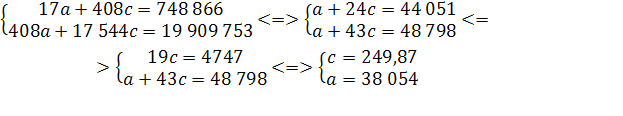
Уравнение регрессии:
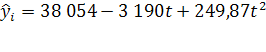 , где , где  =0 в 2001г. =0 в 2001г.
Среднее квадратическое отклонение:

Средняя ошибка прогноза положения параболического тренда на период с номером 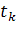 : :
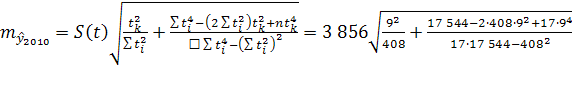 =3 171 =3 171
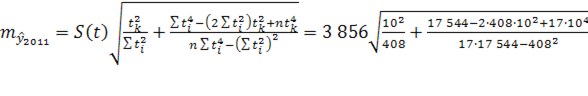 = 3 949 = 3 949
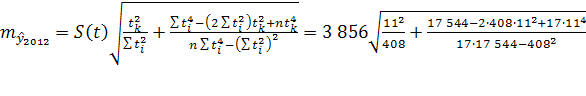 =4830 =4830
Средняя ошибка прогноза:
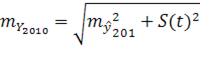 = =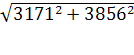 =4 992 =4 992
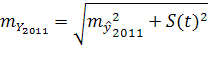 = = = 5519 = 5519
 = =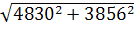 = 6 180 = 6 180
Вероятная ошибка прогноза:

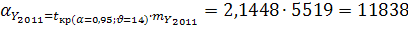
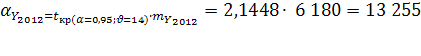
Прогнозные значения:
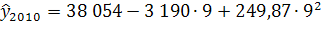 =29 586 =29 586
Доверительный интервал (18 878; 40 294)
 =31 144 =31 144
Доверительный интервал (19 306; 42 982)
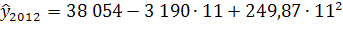 =33 202 =33 202
Доверительный интервал (19 946; 46 457)
Средняя относительная ошибка:
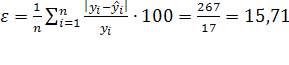 прогноз обладает высокой точностью. прогноз обладает высокой точностью.
| годы |
Число прибывших, человек  |
Условное обозначение времениt
|
 |
 |
 |
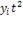 |
Тренд  |
Расчет средней относительной ошибки
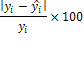
|
 |
| 1993 |
73131 |
-8 |
64 |
4096 |
-585048 |
4680384 |
79 563 |
8,80 |
41 370 292,11 |
| 1994 |
76108 |
-7 |
49 |
2401 |
-532756 |
3729292 |
72 625 |
4,58 |
12 129 198,93 |
| 1995 |
70242 |
-6 |
36 |
1296 |
-421452 |
2528712 |
66 187 |
5,77 |
16 440 106,28 |
| 1996 |
58336 |
-5 |
25 |
625 |
-291680 |
1458400 |
60 249 |
3,28 |
3 660 157,34 |
| 1997 |
57721 |
-4 |
16 |
256 |
-230884 |
923536 |
54 811 |
5,04 |
8 469 953,01 |
| 1998 |
51438 |
-3 |
9 |
81 |
-154314 |
462942 |
49 872 |
3,04 |
2 452 532,97 |
| 1999 |
48267 |
-2 |
4 |
16 |
-96534 |
193068 |
45 433 |
5,87 |
8 031 899,65 |
| 2000 |
43484 |
-1 |
1 |
1 |
-43484 |
43484 |
41 494 |
4,58 |
3 961 416,51 |
| 2001 |
32864 |
0 |
0 |
0 |
0 |
0 |
38 054 |
15,79 |
26 937 481,88 |
| 2002 |
29228 |
1 |
1 |
1 |
29228 |
29228 |
35 114 |
20,14 |
34 648 892,78 |
| 2003 |
29740 |
2 |
4 |
16 |
59480 |
118960 |
32 674 |
9,87 |
8 609 898,77 |
| 2004 |
29701 |
3 |
9 |
81 |
89103 |
267309 |
30 734 |
3,48 |
1 066 941,89 |
| 2005 |
33322 |
4 |
16 |
256 |
133288 |
533152 |
29 293 |
12,09 |
16 230 192,53 |
| 2006 |
29712 |
5 |
25 |
625 |
148560 |
742800 |
28 352 |
4,58 |
1 848 341,97 |
| 2007 |
31949 |
6 |
36 |
1296 |
191694 |
1150164 |
27 911 |
12,64 |
16 302 775,03 |
| 2008 |
25570 |
7 |
49 |
2401 |
178990 |
1252930 |
27 970 |
9,39 |
5 759 675,55 |
| 2009 |
28053 |
8 |
64 |
4096 |
224424 |
1795392 |
28 528 |
1,69 |
225 879,97 |
| Итого |
561 792 |
0 |
408 |
17 544 |
-1 301 385 |
19 909 753 |
748 866 |
131 |
208 145 637 |
| Ср. зн. |
24 |
1032 |
Расчет параметров линейного тренда для абсолютного показателя числа выбывших в Оренбургской области.
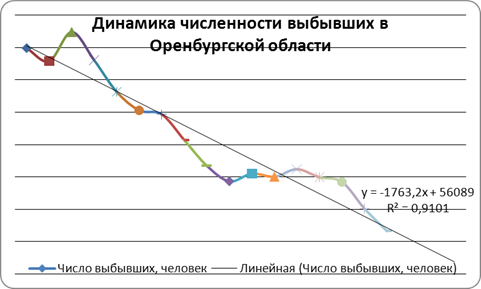
Рис. 6. Динамика числа выбывших в Оренбургской области с линейной линией тренда.
Уравнение имеет вид: 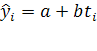 , ,
Где  - уровень тренда для периода или момента с номером - уровень тренда для периода или момента с номером  ; ;
а - свободный член уравнения, равный среднего уровню тренда для периода (момента) с нулевым номером  ; ;
b – главный параметр линейного тренда, его константа, среднее абсолютное изменение за принятую в ряду единицу времени.
Уравнения метода наименьших квадратов:
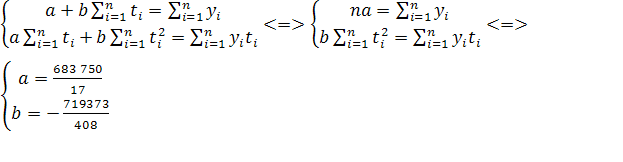
Откуда а
= 40 220,b
= -1 763
 , t=0 в 2001году , t=0 в 2001году
| годы
|
Число выбывших, человек  |
Условное обозначение времениt
|
t
2
|
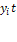 |
Тренд  |
Расчет средней относительной ошибки
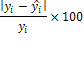
|
| 1993 |
53931 |
-8 |
64 |
-431448 |
56 563 |
4,88 |
| 1994 |
51900 |
-7 |
49 |
-363300 |
53 961 |
3,97 |
| 1995 |
56419 |
-6 |
36 |
-338514 |
51 471 |
8,77 |
| 1996 |
52047 |
-5 |
25 |
-260235 |
49 092 |
5,68 |
| 1997 |
47152 |
-4 |
16 |
-188608 |
46 826 |
0,69 |
| 1998 |
44293 |
-3 |
9 |
-132879 |
44 671 |
0,85 |
| 1999 |
43678 |
-2 |
4 |
-87356 |
42 628 |
2,40 |
| 2000 |
39703 |
-1 |
1 |
-39703 |
40 698 |
2,51 |
| 2001 |
35725 |
0 |
0 |
0 |
38 878 |
8,83 |
| 2002 |
33317 |
1 |
1 |
33317 |
37 171 |
11,57 |
| 2003 |
34506 |
2 |
4 |
69012 |
35 576 |
3,10 |
| 2004 |
34032 |
3 |
9 |
102096 |
34 092 |
0,18 |
| 2005 |
35194 |
4 |
16 |
140776 |
32 721 |
7,03 |
| 2006 |
33940 |
5 |
25 |
169700 |
31 461 |
7,30 |
| 2007 |
33225 |
6 |
36 |
199350 |
30 313 |
8,76 |
| 2008 |
29085 |
7 |
49 |
203595 |
29 276 |
0,66 |
| 2009 |
25603 |
8 |
64 |
204824 |
28 352 |
10,74 |
| Итого
|
683 750
|
0
|
408
|
-719 373
|
683 750
|
88
|
Средняя ошибка прогноза положения о тренда на период с номером 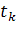 от середины базы расчета тренда имеет вид: от середины базы расчета тренда имеет вид:
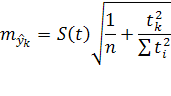
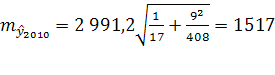 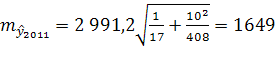

Средняя ошибка прогноза
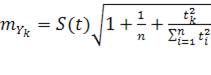
Вероятная ошибка прогноза:
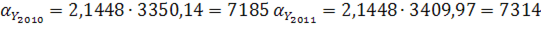
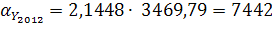
Прогнозные значения:
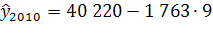 =24 352 =24 352  (17 166; 31 537) (17 166; 31 537)
 =22 589 =22 589  (15 275; 29 902) (15 275; 29 902)
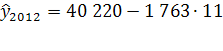 = 20 826 = 20 826  (13 383; 28 267). (13 383; 28 267).
Средняя относительная ошибка:
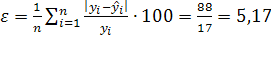
прогноз обладает высокой точностью.
|