Особливості математичних моделей мереж зв’язку
Вступ
Мережа зв'язку це складна система більш високого ієрархічного рівня порівняно з окремою системою зв'язку, математичні моделі якої розглядалися у попередніх підрозділах.
Структура мережі, тобто її топологія, визначається сукупністю пунктів (кінцевих і вузлів комутації) та каналів (ліній) зв'язку, що їх з’єднують. Призначення мережі полягає у передаванні повідомлень від джерел до споживачів інформації.
Характерним для мережі зв'язку є значна кількість джерел та споживачів інформації, а також можливих маршрутів передавання повідомлень.
Тому важливим для мережі є управління процесами передавання повідомлень із оптимальними показниками якості. Модель мережі зв'язку визначається математичним описом структури мережі, а також процесів надходження заявок до кінцевих пунктів та процесів їх обслуговування у мережі. Облуговування включає процеси розподілу інформації у вузлах комутації та процеси доставки повідомлень до споживачів визначеними маршрутами.
При цьому через значну кількість заявок, а також обмежені фізичні можливості систем комутації та каналів (ліній) зв'язку мають місце різні способи обслуговування заявок на вузлах комутації: з втратами (коли заявка одержує відмову на обслуговування), з очікуванням (коли заявка очікує звільнення лінії чи комутуючого пристрою), з обмеженим очікуванням (коли обмежено або число заявок, що очікують, або час очікування).
Таким чином, для математичного опису мереж зв'язку використовують інший математичний аппарат порівняно з описуванням просто систем зв'язку, які у згаданій структурі мережі часто використовуються для з'єднування різних вузлів.
1. Математичний опис структури мережі зв'язку
Розглянемо особливості математичного опису структури мережі зв'язку з використанням мережної математичної моделі.
При цьому як модель використовується граф 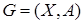 , де , де  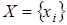 - сукупність вершин графа, які ставляться у відповідність пунктам мережі (кінцевим пунктам, вузлам комутації), а - сукупність вершин графа, які ставляться у відповідність пунктам мережі (кінцевим пунктам, вузлам комутації), а 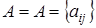 - сукупність ребер графа, які ставляться у відповідність лініям, каналам зв'язку. Відповідно до того, що канали зв’язку можуть бути однобічними та двобічними, ребра графа можуть бути орієнтованими та неорієнтованими. - сукупність ребер графа, які ставляться у відповідність лініям, каналам зв'язку. Відповідно до того, що канали зв’язку можуть бути однобічними та двобічними, ребра графа можуть бути орієнтованими та неорієнтованими.
Таким чином, як модель мережі зв'язку можуть бути використані орієнтовані, неорієнтовані, мішані графи, а також мультиграфи. Мережні моделі широко використовуються на практиці при проектуванні систем електрозв'язку, систем космічного та радіозв'язку, телетрансляційних мереж, обчислювальних комплексів, транспортних мереж.
Мережний аналіз відіграє все більше зростаючу роль, тому що за допомогою графів можна досить просто побудувати модель не тільки мережі зв’язку, але й інших складних системи.
Розширення сфери використання мережної моделі пов'язане з тим,що методи мережного аналізу дають можливість: побудувати модель складної системи як сукупність простих; скласти формально процедури для визначення якісних та кількісних характеристик системи; показати механізм взаємодії компонентів системи з метою опису останньої в термінах їїосновних характеристик; визначити, які дані необхідні для дослідження системи.
При побудові моделей мереж зручно користуватися алгебраїчним зображенням графів, що визначається топологічними матрицями та матрицями характеристик ребер графа (гілок мережі).
Топологічні матриця, що визначає структуру мережі, може задаватися у вигляді матриці суміжності та структурної матриці. Матриця суміжності (сполучення) графа 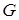 - це квадратна матриця - це квадратна матриця 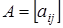 розміру розміру 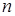 ( (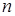 - кількість вершин графа). Вона визначаться таким чином: - кількість вершин графа). Вона визначаться таким чином:
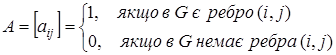 (1) (1)
Елементи головної діагоналі матриці 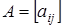 звичайно покладають рівними нулеві звичайно покладають рівними нулеві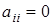 , за винятком випадків, коли в деяких вершинах є "петлі". Матриця , за винятком випадків, коли в деяких вершинах є "петлі". Матриця 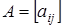 для opiєнтoванro графа несиметрична відносно головної діагоналі, симетричною вона буде лише для нeopiєнтованoго графа. для opiєнтoванro графа несиметрична відносно головної діагоналі, симетричною вона буде лише для нeopiєнтованoго графа.
Структурна матриця використовується для спрощення запису структури мережі, коли ребрам графа присвоюються спеціальні позначення, наприклад,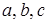 . .
Ці позначення використовуються як елементи структурної матриці. Структурна матриця графа 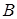 це - квадратна матриця розміру це - квадратна матриця розміру 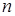 , яка визначається так: , яка визначається так:
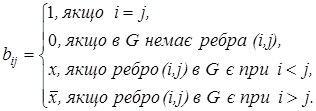 (2) (2)
Kpiм розглянутих топологічних матриць, можуть бути використані матриці інциденцій "вершини-дуги", "дуги-дуги".
Матриця кількісних характеристик ребер графа використовується для різних кількісних оцінок мережі. При цьому кожному ребру графа приписується певна вага - число, яке характеризує яку-небудь властивістъ даного ребра, наприклад, довжину, вартість, пропускну здатність, канальну ємність, час передачі іформації, надійність тощо.
Зазначені характеристики ребер графа подаються у формі відповідних квадратних матриць розміру 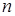 - довжин, вартостей. Якщо - довжин, вартостей. Якщо 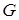 - неорієнтований граф, то yсі матриці симетричні відносно головної діагоналі. - неорієнтований граф, то yсі матриці симетричні відносно головної діагоналі.
Наприклад, для побудови матриці довжин шляхів 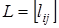 користуються таким правилом: користуються таким правилом:
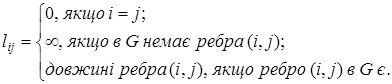 (3) (3)
Матрицю канальних ємностей ребер 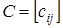 отримують за правилом: отримують за правилом:
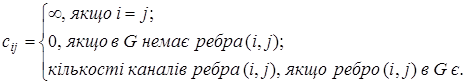 (4) (4)
Аналогічно отримують і інші матриці характеристик ребер графа. Вказані характеристики мережі можуть бути використані при розв’язанні різних задач синтезу та аналізу мереж зв'язку, зокрема, для пошуку оптимальних шляхів передавання повідомлень.
Оскільки призначення мережі зв'язку полягає у тому, щоб надавати абонентам з'єднувальні шляхи для передавання повідомлень відповідно до адреси та заданих показників якості, тому необхідно здійснювати оптимальний вибір з'єднувальних шляхів.
При цьому має здійснюватися вибір таких шляхів, щоб забезпечити найефективніше використання обладнання мережі, або забезпечити мінімально можливі довжину шляхів та кількість транзитних ділянок у шляхах, або забезпечити необхідну кількість каналів у шляхах чи максимальну швидкість передавання.
Так, при розв'язанні задач проектування мереж зв'язку виникає необхідність у пошуку множини шляхів, які існують між заданою парою вузлів зв'язку (вершин графа).
Bcі методи пошуку множини шляхів у мережі можна поділити на два класи: матричні та мережні. Матричні методи грунтуються на перетворенні різних матриць - топологічних чи матриць характеристик ребер графа, а мережні методи - на присвоєнні вершинам графа позначень, що називаються позначками (чи індексами).
Мережні методи визначення множини шляхів між заданими вузлами мережі є графічним еквівалентом матричних методів. Визначення множини шляхів базується на побудові дерева шляхів із фіксованої вершини-витоку (кореня дерева) до решти вершин-стоків графа.
2. Математичні моделі потоків заявок та процесів обслуговування у мережах зв'язку
мережа зв'язок математичний заявка
Окрім структури, математична модель мережі зв'язку повинна описувати потоки заявок та їх обслуговування у мережі. Ці процеси мають стохастичний характер. Розглянемо їх математичні моделі, що будуються на основі теорії випадкових процесів та теорії масового обслуговування.
Основні характеристики випадкових потоків заявок. Випадковий потік заявок розглядається як послідовність випадкових величин, яка може бути задана різними способами, зокрема у вигляді:
- послідовності випадкових моментів часу появи заявки 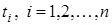 ; ;
-послідовністю випадкових інтервалів часу між заявками
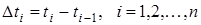 ; ;
-послідовністю випадкових чисел 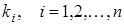 , що визначають кількість заявок на заданих інтервалах часу , що визначають кількість заявок на заданих інтервалах часу 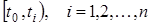 . .
При перших двох способах задання потік заявок розглядається як випадковий точковий процес, а при третьому - як випадковий цілочисельний процес 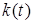 із початковим значенням із початковим значенням 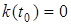 . .
Імовірнісний опис таких випадкових процесів використовує такі характеристики: закон розподілу або відповідну щільність ймовірності моментів часу появи заявок чи інтервалів часу між заявками, а також закон розподілу кількості заявок на заданих інтервалах часу.
В залежності від властивостей цих характеристик розглядаються різні типи потоку заявок: ординарний та неординарний, стаціонарний та нестаціонарний, без післядії та з післядією.
Зокрема, для стаціонарного потоку закон розподілу кількості заявок не залежить від початкового моменту часу. Ординарність означає неможливість одночасного надходження двох і більше заявок. Відсутність післядії означає взаємну незалежність кількостей появи заявок на інтервалах часу, що не перекриваються.
Кількісний опис заявок використовує три основні характеристики:
- провідну функцію потоку, що являє собою середню кількість заявок за інтервал часу  ; ;
- інтенсивність потоку, що являє собою середню кількість заявок за одиницю часу;
- параметр потоку, що визначається імовірністю появи хоча б однієї завки на малому інтервалі часу 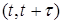 ( (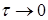 ). ).
Однорідний стаціонарний потік без післядії називається найпростішим потоком. Інтервали часу між заявками в ньому є незалежними випадковими величинами з показниковим розподілом, для якого щільність ймовірності має вигляд
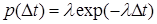 ,(5) ,(5)
де 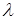 - параметр потоку. - параметр потоку.
Найпростіший потік заявок називається також пуасоновим, бо кількість заявок 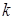 на інтервалі часу тривалістю на інтервалі часу тривалістю  розподілена за законом Пуасона розподілена за законом Пуасона
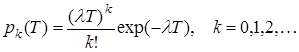 (6) (6)
При застосуванні до найпростішого потоку з параметром 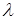 операції проріджування (вилучення із нього частини заявок), одержується рекурентний потік з відновленням. Якщо при цьому операції проріджування (вилучення із нього частини заявок), одержується рекурентний потік з відновленням. Якщо при цьому  заявок підряд втрачається, а залишається тільки кожна заявок підряд втрачається, а залишається тільки кожна 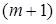 , то проріджений потік має параметр , то проріджений потік має параметр 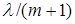 та щільність ймовірності для інтервалів часу між заявками та щільність ймовірності для інтервалів часу між заявками
 (7) (7)
Такий розподіл носить назву розподілу Ерланга  -го порядку, а відповідні потоки називаються ерлангівськими. За допомогою розподілу Ерланга є можливість опису широкого класу потоків - від найпростішого (при -го порядку, а відповідні потоки називаються ерлангівськими. За допомогою розподілу Ерланга є можливість опису широкого класу потоків - від найпростішого (при 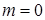 ) до детермінованого з постійною тривалістю інтервалів між заявками (при ) до детермінованого з постійною тривалістю інтервалів між заявками (при 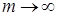 ). ).
Основні характеристики систем масового обслуговування з втратами. Дисципліною обслуговування з явними втратами називається така, при якій заявка, що надходить у систему, отримавши відмову в обслуговуванні, покидає систему.
При обслуговуванні потоку заявок системою кожна з них займає обслуговуючий прилад (канал зв’язку) на деякий інтервал часу. Для систем розподілу інформації як одного із класів систем масового обслуговування важливе значення має сумарний час зайняття каналів при обслуговуванні заявок.
Тому дослідження цих систем проводиться на основі сумарного часу обслуговування заявок, що називається навантаженням. Як правило, розрізняють навантаження, що обслуговується, що надходить і що втрачається.
Навантаження 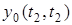 , що обслуговується системою за інтервал часу , що обслуговується системою за інтервал часу 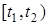 являє собою сумарний час зайняття всіх каналів системи обслуговування потоку заявок, які надходять на її входи за цей інтервал часу являє собою сумарний час зайняття всіх каналів системи обслуговування потоку заявок, які надходять на її входи за цей інтервал часу
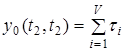 ,(8) ,(8)
де 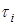 - сума інтервалів часу, протягом яких - сума інтервалів часу, протягом яких 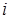 - й канал був зайнятий обслуговуванням на інтервалі часу - й канал був зайнятий обслуговуванням на інтервалі часу 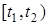 ; ; 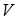 - кількість каналів обслуговування. - кількість каналів обслуговування.
Під інтенсивністю навантаження розуміється навантаження за одиницю часу. Інтенсивність навантаження, що обслуговується, при заданій якості обслуговування характеризує пропускну здатність системи розподілу інформації.
Кількісно вона оцінюється величиною середньої пропускної здатності або середнього часу використання одного каналу
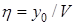 (9) (9)
Під навантаженням 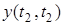 , що надходить у систему за інтервал часу , що надходить у систему за інтервал часу 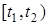 , розуміється таке навантаження, яке може бути обслужене нею за цей інтервал в умовах негайного надання обслуговування кожній заявці, яка надходить. , розуміється таке навантаження, яке може бути обслужене нею за цей інтервал в умовах негайного надання обслуговування кожній заявці, яка надходить.
Навантаження  , що втрачається системою протягом інтервалу часу , що втрачається системою протягом інтервалу часу 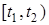 , являє собою різницю між навантаженнями , являє собою різницю між навантаженнями 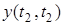 та та 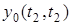 . .
Для кількісної оцінки якості обслуговування з втратами на інтервалі 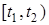 використовуються такі характеристики: втрати за часом, як частина часу на цьому інтервалі, протягом якого всі доступні канали системи зайняті обслуговуванням; втрати за заявками, як відношення числа втрачених за цей відрізок часу заявок до загальної кількості заявок, що надійшли до системи; втрати за навантаженням, як відношення навантаження, що втрачається, до навантаження, що надходить за той же інтервал часу. використовуються такі характеристики: втрати за часом, як частина часу на цьому інтервалі, протягом якого всі доступні канали системи зайняті обслуговуванням; втрати за заявками, як відношення числа втрачених за цей відрізок часу заявок до загальної кількості заявок, що надійшли до системи; втрати за навантаженням, як відношення навантаження, що втрачається, до навантаження, що надходить за той же інтервал часу.
Стани системи обслуговування 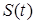 визначаються кількістю заявок, які знаходяться у системі на обслуговуванні. Для дисципліни обслуговування з втратами ця кількість збігається з кількістю зайнятих каналів системи. визначаються кількістю заявок, які знаходяться у системі на обслуговуванні. Для дисципліни обслуговування з втратами ця кількість збігається з кількістю зайнятих каналів системи.
При цьому процес обслуговування системою заявок 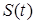 може приймати різні значення в залежності від стану системи: стан може приймати різні значення в залежності від стану системи: стан 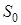 , коли вільні всі , коли вільні всі 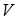 каналів; стан каналів; стан 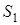 , коли зайнятий один канал, а інші вільні; стан , коли зайнятий один канал, а інші вільні; стан 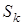 , коли зайнято , коли зайнято 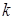 каналів, а інші вільні; каналів, а інші вільні; 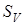 , коли зайняті всі , коли зайняті всі 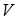 каналів. каналів.
В разі найпростішого потоку заявок з параметром 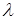 і показниковим розподілом тривалості обслуговування з функцією розподілу і показниковим розподілом тривалості обслуговування з функцією розподілу 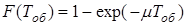 фінальні ймовірності вказаних станів системи фінальні ймовірності вказаних станів системи 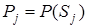 визначаються першою формулою Ерланга визначаються першою формулою Ерланга
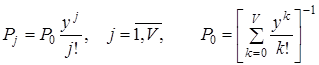 ,(10) ,(10)
де 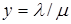 - інтенсивність навантаження, що надходить. - інтенсивність навантаження, що надходить.
Динаміка станів системи обслуговування з втратами для найпростішого або примітивного потоку та показниково розподіленої тривалості обслуговування описується дискретними марківськими процесами народження та загибелі.
При їх імітаційному моделюванні на ЕОМ використовуються ланцюги Маркова із 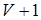 -м станом -м станом 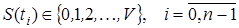 , що створюються на інтервалі часу спостереження у вигляді послідовності відліків у моменти часу , що створюються на інтервалі часу спостереження у вигляді послідовності відліків у моменти часу  . У цих ланцюгах розглядаються переходи між станами через одиничні моменти часу. . У цих ланцюгах розглядаються переходи між станами через одиничні моменти часу.
Аналогічно на основі теорії масового обслуговування будуються математичні моделі складніших систем обслуговування з очікуванням. Дисципліною обслуговування з очікуванням називається така, при якій заявка, що надходить у систему за відсутністю вільних обслуговуючих приладів (каналів), не втрачається, а ставиться до черги, очікуючи звільнення будь якого з них.
Наряду із показниками завантаження каналів система обслуговування з очікуванням додатково описується такими характеристиками: ймовірність умовних втрат за часом, яка визначається середньою часткою часу, коли всі канали зайняті обслуговуванням; ймовірність затримки (очікування початку обслуговування) заявки понад заданий час; середній час очікування обслуговування; ймовірність того, що довжина черги перевищить задану величину; середня довжина черги.
Процес обслуговування описується випадковим процесом, що приймає дикретні значення і визначається кількістю заявок, які присутні у системі обслуговування.
При цьому характерні такі стани системи: стан 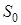 , коли вільні всі , коли вільні всі 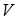 каналів; стан каналів; стан 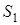 , коли зайнятий один канал, а інші вільні; стан , коли зайнятий один канал, а інші вільні; стан 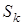 , коли зайнято , коли зайнято 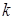 каналів, а інші вільні; стан каналів, а інші вільні; стан 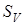 , коли зайняті всі , коли зайняті всі 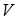 каналів; стан каналів; стан 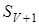 , коли зайняті всі , коли зайняті всі 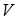 каналів та одна заявка стоїть у черзі; стан каналів та одна заявка стоїть у черзі; стан 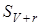 , коли зайняті всі , коли зайняті всі 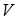 каналів та каналів та 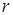 заявок стоїть у черзі. заявок стоїть у черзі.
Довжина черги буде скінченною, якщо інтенсивність навантаження, що надходить, буде меншою за кількість каналів обслуговування у системі. Динаміка станів системи обслуговування з чергами описується дикретними марківськими процесами, зокрема ланцюгами Маркова.
|