Российский Государственный Социальный Университет
Факультет Социальных информационных технологий
Кафедра Информационной безопасности
Курсовая работа
по дисциплине
Системы и сети связи
Москва – 2006
Для системы связи (СС) с переспросом с ожиданием ответа одностороннего действия (рис. 1) при заданных исходных данных:
1. Найти двоичный циклический (n,k)-код Хэмминга, который обеспечивает передачу сообщений в СС с вероятностью выдачи ложного сообщения Рлс(
n
,
k
)
< Pдоп
при следующих условиях:
¾ прямой дискретный канал в СС является двоичным симметричным каналом (ДСК) с постоянными параметрами;
¾ обратный непрерывный канал – без помех;
¾ код используется только для обнаружения ошибок;
¾ найденный значения n и k должны обеспечивать минимум разности Pдоп
-Рлс(
n
,
k
)
для возможных значений n и k.
2. Отложить в координатных осях вычисленные значения Рлс(
n
,
k
)
для всех исследованных пар (n,k). В этих же осях прямой линией изобразить заданное значение Pдоп
.
Исходные данные для курсовой работы (вариант №22):
| Вероятность искажения двоичного символа p |
6x10-4
|
| Допустимая вероятность ложного сообщения Pдоп
|
2x10-7
|
| Допустимое число переспросов s |
∞ |
| Разрядность кода n |
>10 |
| Порождающий многочлен gi
(x) |
g3
(x) |
| Тип кодера |
КД 1 |
| Ввод информационных символов в кодер |
последовательно |
| Тип декодера |
ДК 2 |

Рисунок 1. Структурная схема СС с переспросом с ожиданием ответа одностороннего действия
Описание работы
СС с переспросом с ожиданием ответа одностороннего действия
(рис. 1):
Информационная последовательность отдельными комбинациями не корректирующего кода через первое положение ключа направляется в кодер и в ЗУ передатчика. На выходе кодера образуется комбинация корректирующего кода, которая поступает в модулятор прямого канала. В прямом канале возможно искажение сигнала. На приемной стороне решение о принятом символе принимается демодулятором с так называемой зоной ненадежности.
Принцип его работы можно понять из рисунка.

Пусть символ «1» передается по каналу связи импульсом положительной полярности с амплитудой U, а «0» импульсом отрицательной полярности с той же амплитудой.
В демодуляторе выделена некоторая зона +V –V, если принимаемый импульс попадает в эту зону (зона ненадежности), то демодулятор считает, что он не может принять надежного решения, о том, какой символ передавался. В этом случае, демодулятор выдает символ ненадежности Z. С выхода демодулятора комбинации поступают на вход декодера. После поступления всей комбинации с выхода декодера в обратный канал направляется одна из двух команд:
¾ «переспрос», если содержатся ошибки в принятой комбинации, и одновременно кодовое слово с символами Z стирается;
¾ «продолжение», если не обнаружено ошибок, и комбинация не корректирующего кода направляется к получателю.
Если различитель команд получает команду «продолжения», то из ЗУ передатчика в прямой канал направляется следующая порция* информации. Если различитель команд получает команду «переспрос», то он переключает ключ в положение 2 и из ЗУ передатчика в прямой канал повторно направляется комбинация, которая была стерта.
После выдачи в прямой канал из ЗУ передатчика очередной порции информации, следующая порция не передаётся до тех пор, пока не будет получен ответ по этой порции.
Произведем расчет для (18,13)-кода с d=3.
Для этого введем обозначения:
· Pбо
– вероятность появления на выходе ДСК комбинации (n,k)-кода без ошибок при однократной передаче;
· Роо
– вероятность появления на выходе ДСК комбинации (n,k)-кода с обнаруживаемыми ошибками при однократной передаче;
· Рно
– вероятность появления на выходе ДСК комбинации (n,k)-кода с необнаруживаемыми ошибками при однократной передаче;
· Рi
£
v
о
– вероятность появления на выходе ДСК комбинации с ошибками кратности i£v0
;
· Рi
>
v
о
– вероятность появления на выходе ДСК комбинации с ошибками кратности i>v0
, которые расположены так, что обнаруживаются кодом;
· Рлс
– вероятность появления на выходе СС с неограниченным числом переспросов ложного сообщения.
Найдем:
хэмминг код цикличный программа
Pбо
= qn
, где q=1-p;
Рi
£
v
о
=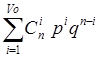 , где v0
=d-1; , где v0
=d-1;
Роо
= Рi
£
v
о
+ Рi
>
v
о
;
Рно
£ 1- Pбо
- Рi
£
v
о
;
Рлс
= Рно
/(1- Роо
).
Пример:
Pбо
= qn
=0,999418
=0,98925490, где q=1-p=0,9994;
Рi
£
v
о
=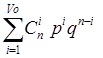 = =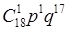 + +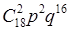 = =
18*0,0006*0,98984881+153*0,00000036*0,99044307=0,01074492, где v0
=d-1=2;
Роо
= Рi
£
v
о
+ Рi
>
v
о
= 0,01074492;
Рно
£ 1- Pбо
- Рi
£
v
о
=1-0,98925490-0,01074492=0,00000018;
Рлс
= Рно
/(1- Роо
)=0,00000018/(1-0,01074492)=0,00000018.


Описание алгоритма:
1) Начало;
2) Объявляем P = 0.0006, Pdop=0.0000002, i=0, k, Pbo, Poo, Pno, Pls, lgPls, h=0, M[61], H[], d=3;
3) Вручную меняем в (по умолчанию d=3);
4) Если d=2, то i=11, иначе переходим к шагу 7;
5) Если i<=31, тоPbo=(1-P)^i, Poo=0, Poo=(C )*(P^1)*(1-P)^(i-1),
Pno=1-Pbo-Poo, Pls=Pno/(1-Poo), lgPls=log10(Pls),
M[i-11]=(Pdop-Pls), i=i+1, переходим к шагу 5, иначе переходим к шагу 35;
6) Выводим Pbo, Poo, Pno, Pls, lgPls, переходим к шагу 5;
7) Если d=3, то i=11, иначе переходим к шагу 21;
8) Если i<=15, то Pbo=(1-P)^i, Poo=0, k=1, иначе переходим к шагу 14;
9) Выводим Pbo;
10) Если k<=2, то Poo=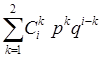 , иначе переходим к шагу 12; , иначе переходим к шагу 12;
11) k=k+1, переходим к шагу 10;
12) Pno=1-Pbo-Poo, Pls=Pno/(1-Poo), lgPls=log10(Pls),
M[i+10]=(Pdop-Pls), i=i+1;
13) Выводим Poo, Pno, Pls, lgPls, переходим к шагу 8;
14) i=17;
15) Если i<=31, то Pbo=(1-P)^i, Poo=0, k=1, иначе переходим к шагу 35;
16) Выводим Pbo;
17) Если k<=2, то Poo=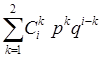 , иначе переходим к шагу 19; , иначе переходим к шагу 19;
18) k=k+1, переходим к шагу 17;
19) Pno=1-Pbo-Poo, Pls=Pno/(1-Poo), lgPls=log10(Pls),
M[i+10]=(Pdop-Pls), i=i+1;
20) Выводим Poo, Pno, Pls, lgPls, переходим к шагу 15;
21) Если d=4, то i=11, иначе переходим к шагу 35;
22) Если i<=15, то Pbo=(1-P)^i, Poo=0, k=1, иначе переходим к шагу 28;
23) Выводим Pbo;
24) Если k<=3, то Poo=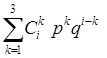 , иначе переходим к шагу 26; , иначе переходим к шагу 26;
25) k=k+1, переходим к шагу 24;
26) Pno=1-Pbo-Poo, Pls=Pno/(1-Poo), lgPls=log10(Pls),
M[i+10]=(Pdop-Pls), i=i+1;
27) Выводим Poo, Pno, Pls, lgPls, переходим к шагу 22;
28) i=17;
29) Если i<=31, то Pbo=(1-P)^i, Poo=0, k=1, иначе переходим к шагу 35;
30) Выводим Pbo;
31) Если k<=3, то Poo=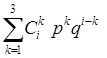 , иначе переходим к шагу 33; , иначе переходим к шагу 33;
32) k=k+1, переходим к шагу 31;
33) Pno=1-Pbo-Poo, Pls=Pno/(1-Poo), lgPls=log10(Pls),
M[i+10]=(Pdop-Pls), i=i+1;
34) Выводим Poo, Pno, Pls, lgPls, переходим к шагу 29;
35) h=0, i=0;
36) Если i<=60, то переходим к шагу 37, иначе переходим к шагу 38;
37) Если M[i]>0, то h=h+1, i=i+1, иначе i=i+1 и переходим к шагу 36;
38) Выделяем память под массив Н из h элементов.
39) Если i<=60, то переходим к шагу 40, иначе переходим к шагу 41;
40) Если M[i]>0, то H[k]=M[i], k=k+1, i=i+1, иначе i=i+1 и переходим к шагу 39;
41) i=0;
42) Ищем минимальный элемент в массиве Н;
43) Если i<=60, то переходим к шагу 44, иначе переходим к шагу 50;
44) Если M[i]=минимальному элементу, то и переходим к шагу 45, иначе i=i+1 и переходим к шагу 43;
45) Если i>=0 и i<=20, то выводим (i+11,i+10)-код, иначе переходим к шагу 46;
46) Если i>=21 и i<=25, то выводим (i-10,i-14)-код, иначе переходим к шагу 47;
47) Если i>=26 и i<=40, то выводим (i-9,i-14)-код, иначе переходим к шагу 48;
48) Если i>=41 и i<=45, то выводим (i-30,i-35)-код, иначе переходим к шагу 49;
49) Если i>=46 и i<=60, то выводим (i-29,i-35)-код, иначе i=i+1 и переходим к шагу 39;
50) Выводим минимальный элемент из массива Н, как минимум разницы Рдоп
-Рлс
;
51) Конец.
Программа написана на языке С++.
#include <vcl.h>
#include <math.h>
#include <stdio.h>
#include <vector>
#include <algorithm>
#pragma hdrstop
#include "Unit1.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
float P = 0.0006;
float Pdop = 0.0000002;
using namespace std;
float M[61];
vector<float>H;
char B[128];
TForm1 *Form1;
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{
}
//---------------------------------------------------------------------------
float C(int n,int m)
{float c=1.0;
for(int i=n;i>=n-m+1;i--)c*=i;
for(int i=1;i<=m;i++)c/=i;
return (int)c;
}
void __fastcall TForm1::ComboBox1Select(TObject *Sender)
{int i=0, k;
double Pbo,Poo,Pno,Pls,lgPls;
AnsiString s;
ListBox1->Clear();
ListBox2->Clear();
ListBox3->Clear();
ListBox4->Clear();
ListBox5->Clear();
ListBox6->Clear();
ListBox7->Clear();
//d=2
if(ComboBox1->ItemIndex==0)
for(i=11;i<=31;i++)
{s="("+IntToStr(i)+","+IntToStr(i-1)+")";
ListBox1->Items->Add(s);
Pbo=pow(1-P,i);
sprintf(B,"%.8f",Pbo);
ListBox2->Items->Add(B);
Poo=0;
Poo=C(i,1)*pow(P,1)*pow(1-P,i-1);
sprintf(B,"%.8f",Poo);
ListBox3->Items->Add(B);
Pno=1-Pbo-Poo;
sprintf(B,"%.8f",Pno);
ListBox4->Items->Add(B);
Pls=Pno/(1-Poo);
sprintf(B,"%.8f",Pls);
ListBox5->Items->Add(B);
lgPls=log10(Pls);
sprintf(B,"%.2f",lgPls);
ListBox6->Items->Add(B);
Series1->AddXY(i,lgPls,s,clRed);
M[i-11]=(Pdop-Pls);
}
//d=3
if(ComboBox1->ItemIndex==1)
{for(i=11;i<=15;i++)
{s="("+IntToStr(i)+","+IntToStr(i-4)+")";
ListBox1->Items->Add(s);
Pbo=pow(1-P,i);
sprintf(B,"%.8f",Pbo);
ListBox2->Items->Add(B);
Poo=0;
for(k=1;k<=2;k++)
Poo+=C(i,k)*pow(P,k)*pow(1-P,i-k);
sprintf(B,"%.8f",Poo);
ListBox3->Items->Add(B);
Pno=1-Pbo-Poo;
sprintf(B,"%.8f",Pno);
ListBox4->Items->Add(B);
Pls=Pno/(1-Poo);
sprintf(B,"%.8f",Pls);
ListBox5->Items->Add(B);
lgPls=log10(Pls);
sprintf(B,"%.2f",lgPls);
ListBox6->Items->Add(B);
Series2->AddXY(i,lgPls,s,clLime);
M[i+10]=(Pdop-Pls);
}
for(i=17;i<=31;i++)
{s="("+IntToStr(i)+","+IntToStr(i-5)+")";
ListBox1->Items->Add(s);
Pbo=pow(1-P,i);
sprintf(B,"%.8f",Pbo);
ListBox2->Items->Add(B);
Poo=0;
for(k=1;k<=2;k++)
Poo+=C(i,k)*pow(P,k)*pow(1-P,i-k);
sprintf(B,"%.8f",Poo);
ListBox3->Items->Add(B);
Pno=1-Pbo-Poo;
sprintf(B,"%.8f",Pno);
ListBox4->Items->Add(B);
Pls=Pno/(1-Poo);
sprintf(B,"%.8f",Pls);
ListBox5->Items->Add(B);
lgPls=log10(Pls);
sprintf(B,"%.2f",lgPls);
ListBox6->Items->Add(B);
Series2->AddXY(i,lgPls,s,clLime);
M[i+9]=(Pdop-Pls);
}
}
//d=4
if(ComboBox1->ItemIndex==2)
{for(i=11;i<=15;i++)
{s="("+IntToStr(i)+","+IntToStr(i-5)+")";
ListBox1->Items->Add(s);
Pbo=pow(1-P,i);
sprintf(B,"%.8f",Pbo);
ListBox2->Items->Add(B);
Poo=0;
for(k=1;k<=3;k++)
Poo+=C(i,k)*pow(P,k)*pow(1-P,i-k);
sprintf(B,"%.8f",Poo);
ListBox3->Items->Add(B);
Pno=1-Pbo-Poo;
sprintf(B,"%.8f",Pno);
ListBox4->Items->Add(B);
Pls=Pno/(1-Poo);
sprintf(B,"%.8f",Pls);
ListBox5->Items->Add(B);
lgPls=log10(Pls);
sprintf(B,"%.2f",lgPls);
ListBox6->Items->Add(B);
Series3->AddXY(i,lgPls,s,clYellow);
M[i+30]=(Pdop-Pls);
}
for(i=17;i<=31;i++)
{s="("+IntToStr(i)+","+IntToStr(i-6)+")";
ListBox1->Items->Add(s);
Pbo=pow(1-P,i);
sprintf(B,"%.8f",Pbo);
ListBox2->Items->Add(B);
Poo=0;
for(k=1;k<=3;k++)
Poo+=C(i,k)*pow(P,k)*pow(1-P,i-k);
sprintf(B,"%.8f",Poo);
ListBox3->Items->Add(B);
Pno=1-Pbo-Poo;
sprintf(B,"%.8f",Pno);
ListBox4->Items->Add(B);
Pls=Pno/(1-Poo);
sprintf(B,"%.8f",Pls);
ListBox5->Items->Add(B);
lgPls=log10(Pls);
sprintf(B,"%.2f",lgPls);
ListBox6->Items->Add(B);
Series3->AddXY(i,lgPls,s,clYellow);
M[i+29]=(Pdop-Pls);
}
}
int h=0;
for (i=0;i<=60;i++)
if (M[i]>0) h++;
H.resize(h);
k=0;
for (i=0; i<=60;i++)
if (M[i]>0) {H[k]=M[i]; k++;}
for (i=0;i<=60;i++)
if (M[i]==*min_element(H.begin(),H.end()))
{if (i>=0&&i<=20)
{s="("+IntToStr(i+11)+","+IntToStr(i+10)+")-кодс d=2";
ListBox7->Items->Add(s);}
if (i>=21&&i<=25)
{s="("+IntToStr(i-10)+","+IntToStr(i-14)+")-кодс d=3";
ListBox7->Items->Add(s);}
if (i>=26&&i<=40)
{s="("+IntToStr(i-9)+","+IntToStr(i-14)+")-кодс d=3";
ListBox7->Items->Add(s);}
if (i>=41&&i<=45)
{s="("+IntToStr(i-30)+","+IntToStr(i-35)+")-кодс d=4";
ListBox7->Items->Add(s);}
if (i>=46&&i<=60)
{s="("+IntToStr(i-29)+","+IntToStr(i-35)+")-кодс d=4";
ListBox7->Items->Add(s);}
}
ListBox7->Items->Add("");
ListBox7->Items->Add("Минимальная разность");
sprintf(B,"%.12f",*min_element(H.begin(),H.end()));
ListBox7->Items->Add("Рдоп-Рлс");
ListBox7->Items->Add(B);
}
//---------------------------------------------------------------------------
void __fastcall TForm1::FormCreate(TObject *Sender)
{ComboBox1->ItemIndex=1;
Series4->AddXY(0,log10(Pdop),"lg Pдоп",clBlack);
Series4->AddXY(31.3,log10(Pdop),"lg Pдоп",clBlack);
}
//---------------------------------------------------------------------------

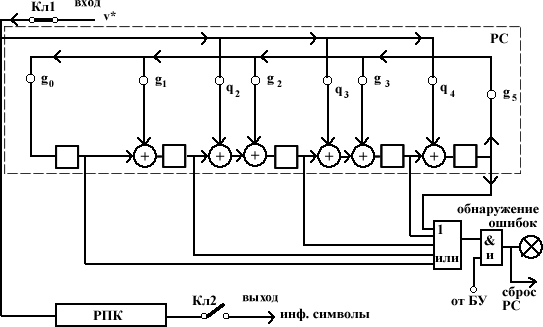
Построить функциональные схемы кодера и декодера для найденного (n,k)-кода и заданного для него порождающего многочлена g3
(X). При изображении схем кодера и декодера использовать условные изображения элементов:

элемент умножения
|

элемент памяти
|

элемент сложения по модулю 2
|
Исходные данные:
g3
(x)=x5
+x3
+x2
+x+1;
r=5.
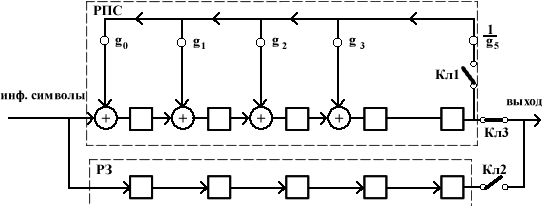
Функциональная
схема кодера для (18,13)-кода
Описание работы схемы:
Кодер 1 с последовательным вводом информационных символов (a12
, a11
, …, a1
, a0
) состоит из регистра проверочных символов (РПС), регистра задержки (РЗ) с 5 элементами памяти и трех ключей. В исходном состоянии в элементах памяти регистров – нули, ключи Кл1 и Кл2 разомкнуты, Кл3 замкнут.
При подаче первых 5 импульсов сдвига (ИС) 5 информационных символов, начиная со старшего, вводятся в оба регистра. С окончанием 5-го ИС ключи Кл1 и Кл2 замыкаются, а Кл3 размыкается.
В течение последующих k ИС информационные символы выводятся из РЗ, а в РПС образуются 5 проверочных символов. После этого ключи Кл1 и Кл2 размыкаются, а Кл3 замыкается.
За последующие 5 импульсов сдвига проверочные символы выдаются на выход кодера, после чего схема возвращается в исходное состояние. Таким образом, первый символ комбинации УЦК появляется на выходе кодера с задержкой на 5 ИС.
1. Хохлов Г.И., Пособие к выполнению лабораторной работы №3 по дисциплине «Системы и сети связи». – М.: 2005. – 18 с.
2. Хохлов Г.И., Пособие по выполнению курсовой работы по дисциплине «Системы и сети связи». – М.: 2005. – 15 с.
|