МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное агентство по образованию
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ (МГСУ)
Факультет ПГС-о
Кафедра Металлические конструкции
КУРСОВОЙ ПРОЕКТ
По дисциплине
Металлические конструкции
Тема:
Проектирование и расчет балочной клетки
Выполнил студент
Поздняков Н.В., ПГС-о,
IV
курс, 2 группа
Руководитель проекта
Морозова Д.В.
МЫТИЩИ 2005 г.
Содержание
1. Исходные данные
2. Выбор схемы балочной клетки
2.1 Расчет настила
2.2 Усложненный тип балочной клетки
3. Проектирование и расчет главных балок
3.1 Изменение сечения главной балки по длине
3.2 Проверка прочности и общей устойчивости главной балки
3.3 Проверка местной устойчивости сжатого пояса и стенки сварной балки
3.4 Расчет поясных швов главной балки
3.5 Расчет опорного ребра главной балки
3.6 Проектирование стыка главной балки на высокопрочных болтах
3.7 Проектирование сварного стыка главной балки
4. Проектирование и расчет колонн
4.1 Расчетная схема и расчетная длина колонны
4.2 Определение продольной силы в колонне, выбор типа сечения колонны
4.3 Подбор сечения, проверка общей устойчивости колонн и местной устойчивости стенки и полок
4.4 Расчет и конструирование оголовка колонны
4.5 Расчет и конструирование базы колонны
Список используемой литературы
1. Исходные данные
| Шаг колонн в продольном направлении А, м |
16 |
| Шаг колонн в поперечном направлении B, м |
6 |
| Габариты площадки в плане |
3Ах3В |
| Отметка верха настила, м |
9 |
| Строительная высота перекрытия, м |
не ограничена |
| Временная равномерно распределенная нагрузка, кН/м2
|
22 |
Материал конструкций:
настила
балок настила и вспомогательных
главных балок
колонн
фундамента
|
сталь С235
сталь С245
сталь С255
сталь С275
бетон В12,5
|
| Допустимый относительный прогиб настила |
1/120 |
Тип сечения колонны
Сопряжение колонны с фундаментом
|
сплошная
шарнирное
|
2. Выбор схемы балочной клетки
балочная клетка настил прочность колонна

2.1 Расчет настила
Несущий настил состоит из стального листа, уложенного на балки и приваренного к ним.
Уже заранее зная оптимальную толщину настила, приведем подбор настила и балок настила именно для этой толщины.
По графику зависимости l
/
t
для листового настила шарнирно закрепленными краями от заданного прогиба и нормативной нагрузки на настил получаем l
/
t
=
150.
Определим расход металла при толщине настила t
= 6 мм и t
= 12 мм.
При t
= 6 мм
l=150х6=900 мм, тогда число балок настила равно n=16000/900= =17,78 шагов или 18 балок.
Принимаем n = 18 , a1
= 900 мм.
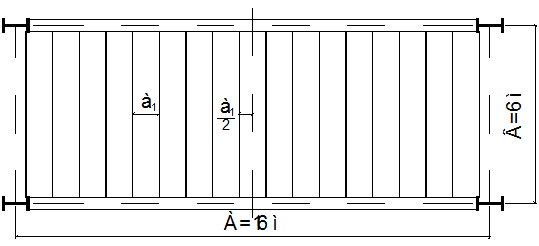
Схема нормального типа балочной клетки при
t
=6 мм и а1
=900 мм
При t
= 12 мм
l=150х12=1800 мм, т.к. рекомендованный шаг балок настила находиться в пределах от 750 до 1200 мм, то принимаем l=1200 мм, тогда число балок настила равно n=16000/1200=13,33 шага или 14 балок. Принимаем n = 14, a2
= 1200 мм.
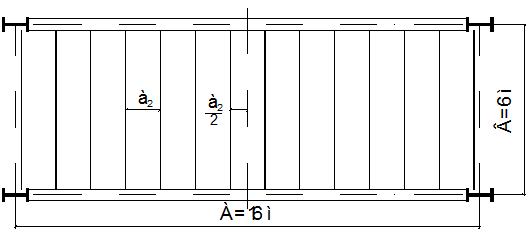
Схема нормального типа балочной клетки при
t
=12 мм и а2
=1200 мм
2.1.1 Рассматриваем 1 вариант при
t
н
= 6 мм
Толщина настила tн
= 6 мм
Вес настила r = 7,85 г/см3
= 7850 кг/м3
при tн
= 6 мм вес gn
= 0,471 кН/м2
Расчетная схема балок настила

Нормативная нагрузка на балку настила
qn
= (pn
+gn
)·a1
= (22+0,471)·0,9 = 20,22 кН/м
Расчетная нагрузка на балку настила
q= (gp
·pn
+ gg
·gn
)· a1
= (1,2·22 + 1,05·0,471)·0,9 =24,21 кН/м
gp
= 1,2, gg
= 1,05 – коэффициенты надежности
Расчетный изгибающий момент (длина балки настила 6 м)
 кН
×
м
= 10892 кН
×
см
. кН
×
м
= 10892 кН
×
см
.
Требуемый момент сопротивления балки настила:
 см3
. см3
.
При условии Wx
>Wтр
по ГОСТ 8239-72 принимаем стальной горячекатанный двутавр № 30 с уклоном внутренних граней полок. Для него из сортамента выписываем: Wx
= 472 см3
; Ix
= 7080 см4
; g = 36,5 кг/м, ширина полки b=135 мм.
Так как W= 472
см3
>Wр,тр
= 412,58 см3
, то проверяем только прогиб балки настила по формуле:
 , ,
здесь l – длина изгибаемой балки, в нашем случае это В=600 см.
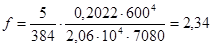 см. см.
По формуле находим, что наибольший допустимый прогиб для балки такой длины составляет:
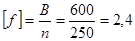 см. см.
f = 2,34 < 2,4 = [f], следовательно принятая балка удовлетворяет условиям прочности и прогиба. Проверку касательных напряжений в прокатных балках при отсутствии ослабления опорных сечений обычно не производят, так как она легко удовлетворяется из-за относительно большой толщины стенок балок.
Общую устойчивость балок настила проверять не надо, так как их сжатые пояса надежно закреплены в горизонтальном направлении приваренным к ним настилом.
Выбранная балка настила проходит по всем проверкам.
Вычислим общую массу настила и балок настила на одном пролете:
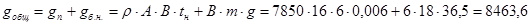 кг
, кг
,
тогда расход металла на 1 м2
будет:
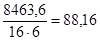 кг/м2
. кг/м2
.
2.1.2 Рассматриваем 2 вариант при
t
н
= 12 мм
Толщина настила tн
= 12 мм
Вес настила r = 7,85 г/см3
= 7850 кг/м3
при tн
= 12 мм вес gn
= 0,942 кН/м2
Нормативная нагрузка на балку настила
qn
= (pn
+gn
)·a2
= (22+0,942)·1,2 = 27,53 кН/м
Расчетная нагрузка на балку настила
q= (gp
·pn
+ gg
·gn
)·a2
= (1,2·22 + 1,05·0,942)·1,2 =32,87 кН/м
gp
= 1,2, gg
= 1,05 – коэффициенты надежности
Расчетный изгибающий момент (длина балки настила 6 м)
 кН
×
м
= 14790 кН
×
см
. кН
×
м
= 14790 кН
×
см
.
Требуемый момент сопротивления балки настила:
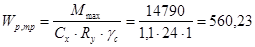 см3
. см3
.
При условии Wx
>Wтр
по ГОСТ 8239-72 принимаем стальной горячекатанный двутавр № 33 с уклоном внутренних граней полок. Для него из сортамента выписываем: Wx
= 597 см3
; Ix
= 9840 см4
; g = 42,2 кг/м, ширина полки b=140 мм.
Так как W = 597 см3
>Wр,тр
= 560,23 см3
, то проверяем только прогиб балки настила по формуле:
 , ,
здесь l – длина изгибаемой балки, в нашем случае это В=600 см.
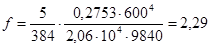 см. см.
По формуле находим, что наибольший допустимый прогиб для балки такой длины составляет:
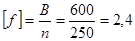 см. см.
f = 2,29 < 2,4 = [f], следовательно принятая балка удовлетворяет условиям прочности и прогиба. Проверку касательных напряжений в прокатных балках при отсутствии ослабления опорных сечений обычно не производят, так как она легко удовлетворяется из-за относительно большой толщины стенок балок.
Общую устойчивость балок настила проверять не надо, так как их сжатые пояса надежно закреплены в горизонтальном направлении приваренным к ним настилом.
Вычислим общую массу настила и балок настила на одном пролете:
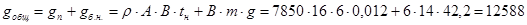 кг
, кг
,
тогда расход металла на 1 м2
будет:
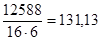 кг/м2
. кг/м2
.
2.2 Усложненный тип балочной клетки
В усложненном типе балочной клетки балки настила, в отличии от нормального типа, опираются не на главные балки, а на вспомогательные.
Выберем шаг вспомогательных балок - l. Он должен быть в пределах от 3 до 4 м. Примем l = 4 м, т.е. при разбиении А=16 м на 4 части.
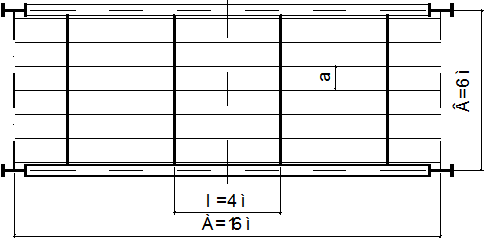
Схема усложненного типа балочной клетки.
Подбор настила
Настил будем выбирать из соображений экономии металла и принятой за минимальный шаг балок настила 900 мм.
Число балок настила равно n = 6000/900 = 6,67 шагов или 7 балок.
Толщина настила tн
= 6 мм вес gn
= 0,471 кН/м2
Нормативная нагрузка на балку настила
qn
= (pn
+gn
)·a = (22+0,471)·0,9 = 20,22 кН/м
Расчетная нагрузка на балку настила
q= (gp
·pn
+ gg
·gn
)·a = (1,2·22 + 1,05·0,471)·0,9 =24,21 кН/м
gp
= 1,2, gg
= 1,05 – коэффициенты надежности
Расчетная схема балок настила
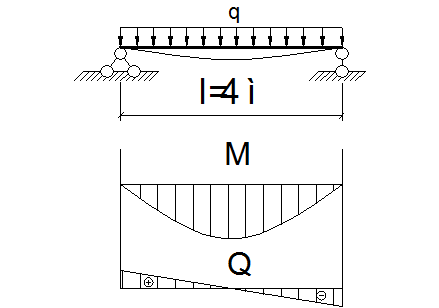
Расчетный изгибающий момент (длина балки настила 4 м)
 кН
×
м
= 4842 кН
×
см
. кН
×
м
= 4842 кН
×
см
.
Требуемый момент сопротивления балки настила:
 см3
. см3
.
При условии Wx
>Wтр
по ГОСТ 8239-72 принимаем стальной горячекатанный двутавр № 22 с уклоном внутренних граней полок. Для него из сортамента выписываем: Wx
= 232 см3
; Ix
= 2550 см4
; g = 24 кг/м, ширина полки b=110 мм.
Проверим подобранную балку настила на наличие пластических деформаций:
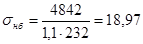 кН/см2
< 24кН/см2
. кН/см2
< 24кН/см2
.
Проверяем прогиб балки настила по формуле:
 , ,
здесь l – длина изгибаемой балки, в нашем случае это l=400 см.
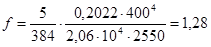 см. см.
По формуле находим, что наибольший допустимый прогиб для балки такой длины составляет:
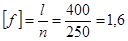 см. см.
f = 1,28 < 1,6 = [f], следовательно принятая балка удовлетворяет условиям прочности и прогиба. Проверку касательных напряжений в прокатных балках при отсутствии ослабления опорных сечений обычно не производят, так как она легко удовлетворяется из-за относительно большой толщины стенок балок.
Общую устойчивость балок настила проверять не надо, так как их сжатые пояса надежно закреплены в горизонтальном направлении приваренным к ним настилом.
Определение силы растягивающая настил и катет сварного шва
По первому предельному состоянию найдем распор Н
:
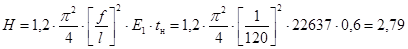 кН/см
. кН/см
.
 - приведенный модуль жесткости. - приведенный модуль жесткости.
Таким образом для нашего случая получим
 кН/см2
, кН/см2
,
Определим катет шва сварного соединения настила и балки настила:
 , (2) , (2)
где b
f
- коэффициент, принимаем при полуавтоматической сварке элементов из стали по СНиП
II
-23-81*
таблица 34 равным 0,9;
lw
– расчетная длина шва, принимаем равной = 1 см
;
Rwf
– расчетное сопротивление угловых швов срезу по металлу шва, по СНиП
II
-23-81*
таблица 3 определяется как:
 , ,
где Rwun
– нормативное сопротивления металла шва по временному сопротивлению, определяем по СНиП
II
-23-81*
таблица 56 для электрода типа Э42 и марки проволоки Св-08 равно 41 кН/см2
;
g
wm
– коэффициент надежности по материалу по металлу шва, по СНиП
II
-23-
81 таблица 3 равен 1,25.
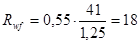 кН/см2
. кН/см2
.
Таким образом с учетом этого расчетная толщина шва сварного соединения настила и балок настила по формуле (1) будет
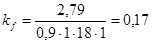 см
. см
.
Принимаем kw
= 4 мм
, так как это минимально допустимый катет.
Подбор вспомогательных балок
Материал вспомогательных балок – сталь С245, имеющая расчетное сопротивление растяжению, сжатию и изгибу по пределу текучести Ry
= 24 кН/см2
.
Воспользуемся правилом: если количество шагов балок настила £ 5, то нагрузка воспринимаемая вспомогательными балками считается как действие сосредоточенных сил; если > 5, то нагрузка на вспомогательную балку принимается равномерно распределенной. Итак, m = 7 > 5, следовательно, для вспомогательной принимаем такую же расчетную схему, как для балки настила.
Вес балок настила:
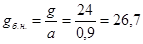 кг/м2
. кг/м2
.
Тогда нормативная нагрузка на вспомогательную балку без учета собственного веса вспомогательных балок будет равна
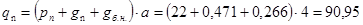 кН/м = 0,9095 кН/см. кН/м = 0,9095 кН/см.
Расчетная нагрузка на вспомогательную балку c учетом собственного веса вспомогательных балок будет равна
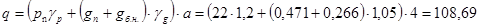 кН/м=1,089 кН/см кН/м=1,089 кН/см
С учетом принятой расчетной схемы и того, что на балку настила действует равномерно распределенная нагрузка, расчетный максимальный изгибающий момент найдем по формуле:
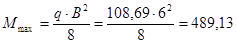 кН×м = 48913 кН×см. кН×м = 48913 кН×см.
Требуемый момент сопротивления вспомогательной балки:
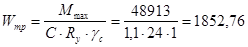 см3
. см3
.
При условии Wx
> Wтр
по ГОСТ 26020-83 принимаем стальной горячекатанный двутавр № 55Б1 с параллельными гранями полок. Для него из сортамента выписываем: Wx
= 2051 см3
; Ix
= 55680 см4
; g = 89 кг/м; b = 220 мм; t = 13,5 мм.
Проверим подобранную балку настила на наличие пластических деформаций по следующей формуле:
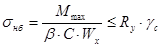 , ,
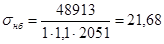 кН/см2
< 24кН/см2
. кН/см2
< 24кН/см2
.
Проверим прогиб балки настила по формуле:
 , ,
здесь l – длина изгибаемой балки, в нашем случае это В = 600см.
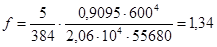 см. см.
По формуле находим, что наибольший допустимый прогиб для балки такой длины составляет:
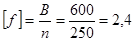 см. см.
f = 1,34 < 2,4 = [f], следовательно принятая балка удовлетворяет условиям прогиба.
Проверим общую устойчивость вспомогательных балок в середине пролета, в сечении с наибольшими нормальными напряжениями. Их сжатый пояс закреплен от перемещений балками настила, которые вместе с приваренным к ним настилом образуют жесткий диск, и за расчетный пролет следует принимать расстояние между балками настила lef
= 900 мм. Условие устойчивости записывается в виде:
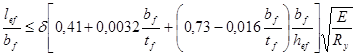 , ,
где lef
– расчетная длина балки между связями, препятствующими поперечным смещениям сжатого пояса балки;
bf
– ширина сжатого пояса (ширина полки);
tf
– толщина сжатого пояса (толщина полки);
hef
– расстояние (высота) между осями поясных листов.
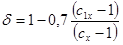 . .
Условия применения уравнения устойчивости плоской формы изгиба:
 применение формулы возможно. применение формулы возможно.
При t=0 и с1х
=сх
получаем  , ,
 . .
Таким образом, принятое сечение удовлетворяет требованиям устойчивости.
Вычислим общую массу настила, балок настила и вспомогательных балок на одном пролете:
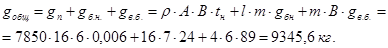
тогда расход металла на 1 м2
будет:
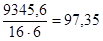 кг/м2
. кг/м2
.
| Тип балочной системы |
Масса, кг |
| Настил |
Балки настила |
Второстепенные балки |
На один пролет |
На 1 м2
|
| 1 |
4521,6 |
3942 |
- |
8463,6 |
88,16 |
| 2 |
9043,2 |
3544,8 |
- |
12588 |
131,13 |
| 3 |
4521,6 |
2688 |
2136 |
9345,6 |
97,35 |
По расходу металла выгоднее нормальный (1) тип балочной клетки при t=6 мм.
Таким образом принимаем балочную клетку нормального типа с настилом толщиной 6 мм и балками настила из стального горячекатаного двутавра № 30 с уклоном внутренних граней полок.
3. Проектирование и расчет главных балок
Главные балки, несущие балки настила, являются балками составного сечения. Составные балки используются в тех случаях, когда прокатные балки не удовлетворяют хотя бы одному из условий – прочности, жесткости, общей устойчивости. Проверим необходимость использования составного сечения.
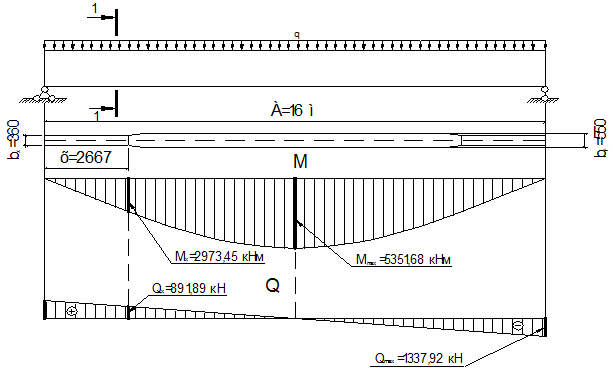
Расчетная схема для главной балки будет выглядеть, как показано на рисунке (см. ниже). Здесь же построены эпюры изгибающих моментов М и поперечных сил Q.

Вес балок настила
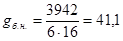 кг/м2
= 0,411 кН/м2
. кг/м2
= 0,411 кН/м2
.
Нормативная нагрузка на главную балку без учета собственного веса главной балки
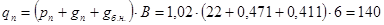 кН/м = 1,4 кН/см. кН/м = 1,4 кН/см.
Расчетная нагрузка на главную балку с учетом собственного веса главной балки
 кН/м= кН/м=
= 1,6724 кН/см
 С учетом принятой расчетной схемы и того, что на главную балку действует равномерно распределенная нагрузка, расчетный максимальный изгибающий момент в середине пролета найдем по формуле: С учетом принятой расчетной схемы и того, что на главную балку действует равномерно распределенная нагрузка, расчетный максимальный изгибающий момент в середине пролета найдем по формуле:
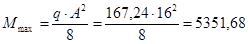 кН×м = 535168 кН×см. кН×м = 535168 кН×см.
Максимальное значение поперечная сила принимает на опорах и равняется:
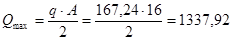 кН. кН.
Главную балку рассчитываем с учетом развития пластических деформаций. Требуемый момент сопротивления главной балки, первоначально принимая с=1,1:
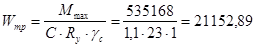 см3
. см3
.
Условие Wx
> Wтр
не выполняется ни для одной прокатной балки даже если не учитывать собственный вес при подсчете нагрузки на балку. Таким образом будем подбирать составное сечение главной балки.
Сечение главной балки будем подбирать двутаврового типа, состоящего из из трех листов: вертикального – стенки и двух горизонтальных – полок, которые сваривают в заводских условиях автоматической сваркой.
Запишем необходимые для расчета величины:
- материал главной балки – сталь С255;
- расчетное сопротивление стали растяжению, сжатию и изгибу Ry
= 23 кН/см2
при t³ 20 мм принимаем по ГОСТ 27772-88;
- расчетное сопротивление стали сдвигу RS
принимаем по СНиП II-23-81* (1990) табица 1:
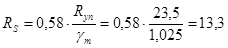 кН/см2
. кН/см2
.
- строительная высота перекрытия hстр
– не ограничена
- прогиб f
< (1/400)
l
 Масса балки состоит из массы ее поясов, стенки и некоторых конструктивных элементов (стыковых накладок, ребер жесткости), учитываемых строительным коэффициентом, причем с увеличением высоты балки масса поясов уменьшается, а масса стенки возрастает. Так как, как видно из рисунка, функции массы поясов и стенки с изменением высоты балки изменяются неодинаково – одна убывает, а другая возрастает, то существует наименьшее значение суммы обеих функций, т.е. должна быть высота, при которой суммарная масса поясов и стенки будет наименьшей. Масса балки состоит из массы ее поясов, стенки и некоторых конструктивных элементов (стыковых накладок, ребер жесткости), учитываемых строительным коэффициентом, причем с увеличением высоты балки масса поясов уменьшается, а масса стенки возрастает. Так как, как видно из рисунка, функции массы поясов и стенки с изменением высоты балки изменяются неодинаково – одна убывает, а другая возрастает, то существует наименьшее значение суммы обеих функций, т.е. должна быть высота, при которой суммарная масса поясов и стенки будет наименьшей.
Определим оптимальную высоту
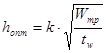 балки, предварительно задав ее высоту: балки, предварительно задав ее высоту:
h
»
(1/10)
l
»
1,6 м
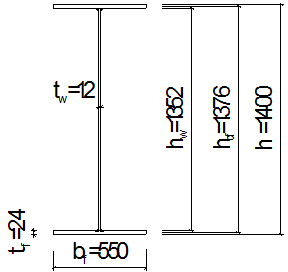
и рассчитав толщину стенки
tw
= 7+3·1600/1000 = 11,8 мм = 12 мм
По справочным данным определим, что k = 1,15.
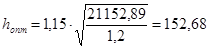 см = 150 см. см = 150 см.
Из условия жесткости главной балки найдем величину минимальной высоты главной балки hmin
:
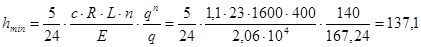 см. см.
В целях унификации конструкции примем окончательное значение высоты балки кратное 100 мм, т.е. h
=
140 см.
Проверяем принятую толщину стенки:
по эмпирической формуле
tw
= 7+3·1400/1000 = 11,2 мм
из условия работы стенки на касательные напряжения на опоре
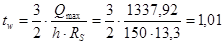 см < 1,2 см см < 1,2 см
Чтобы не применять продольных ребер жесткости
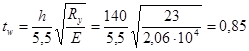 см < 1,2 см. см < 1,2 см.
Сравнивая полученную расчетным путем толщину стенки с принятой (12 мм), приходим к выводу, что она удовлетворяет условию прочности на действие касательных напряжений и не требует укрепления ее продольным ребром жесткости для обеспечения местной устойчивости.
Найдем размеры горизонтальных листов пояса исходя из необходимой несущей способности балки. Для этого вычислим требуемый момент инерции сечения балки:
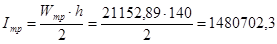 см4
, см4
,
который распределяется на момент инерции стенки и двух поясов балки:
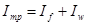 . .
Принимаем толщину поясов балки tf
= 20 мм, тогда высота стенки балки будет равной
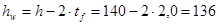 см, см,
Момент инерции стенки балки
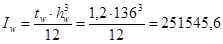 см4
. см4
.
Момент инерции, приходящийся на поясные листы
 см4
. см4
.
Момент инерции поясных листов балки относительно ее нейтральной оси, пренебрегая моментом инерции поясов относительно их собственной оси ввиду его малости, будет равен
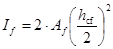 , ,
где h- расстояние между параллельными осями поясов балки
 см. см.
Отсюда получаем требуемую площадь сечения поясов балки
 см2
. см2
.
Находим требуемое значение ширины пояса балки:
 см. см.
Окончательно примем bf
= 650 мм.
Принимаем пояса из универсальной стали 650х20 мм, для которой  , что находится в пределах рекомендуемого отношения. , что находится в пределах рекомендуемого отношения.
Уточняем принятый ранее коэффициент учета пластической работы с
исходя из:
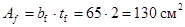 ; ;
 ; ;
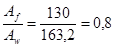
Принимаем с=1,08, которое практически соответствует заданному с=1,1
Проверим отношение ширины свеса сжатого пояса к его толщине из соображений местной устойчивости ( по п.7.24 СНиП II-23-81* ):
 принятое соотношение размеров пояса не удовлетворяет условию его местной устойчивости. Увеличим толщину поясов балки до tf
= 24 мм и произведем новый расчет. принятое соотношение размеров пояса не удовлетворяет условию его местной устойчивости. Увеличим толщину поясов балки до tf
= 24 мм и произведем новый расчет.
Принимаем толщину поясов балки tf
= 24 мм, тогда высота стенки балки будет равной
 см, см,
Момент инерции стенки балки
 см4
. см4
.
Момент инерции, приходящийся на поясные листы
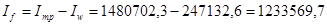 см4
. см4
.
Момент инерции поясных листов балки относительно ее нейтральной оси, пренебрегая моментом инерции поясов относительно их собственной оси ввиду его малости, будет равен
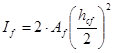 , ,
где h- расстояние между параллельными осями поясов балки
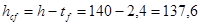 см. см.
Отсюда получаем требуемую площадь сечения поясов балки
 см2
. см2
.
Находим требуемое значение ширины пояса балки:
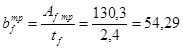 см. см.
Окончательно примем bf
= 550 мм.
Принимаем пояса из универсальной стали 550х24 мм, для которой 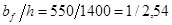 , что находится в пределах рекомендуемого отношения. , что находится в пределах рекомендуемого отношения.
Уточняем принятый ранее коэффициент учета пластической работы с
исходя из:
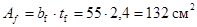 ; ;
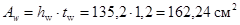 ; ;

Принимаем с=1,09, которое практически соответствует заданному с=1,1
Проверим отношение ширины свеса сжатого пояса к его толщине из соображений местной устойчивости (по п.7.24 СНиП II-23-81*):
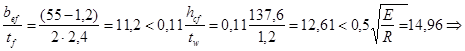 принятое соотношение размеров пояса удовлетворяет условию его местной устойчивости. принятое соотношение размеров пояса удовлетворяет условию его местной устойчивости.
Проверяем несущую способность балки исходя из устойчивости стенки в области пластических деформаций балки в месте действия максимального момента, где Q=0 и τ=0.
 ; ;
 где где
Подобранное сечение балки проверяем на прочность. Определим момент инерции балки:
 см4
. см4
.
Определим момент сопротивления балки:
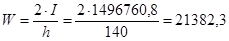 см3
. см3
.
Проверим нормальные напряжения в балке по следующей формуле:
 , ,
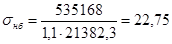 кН/см2
< 23×1 = 23 кН/см2
, кН/см2
< 23×1 = 23 кН/см2
,
следовательно, подобранное сечение удовлетворяет условию прочности и не имеет недонапряжений больше 5%.
Проверку прогиба делать нет необходимости, так как принятая высота сечения главной балки больше минимальной и регламентированный прогиб будет обеспечен.
3.1 Изменение сечения главной балки по длине
В разделе (3) я считал, что сечение главной балки остается постоянным по всей длине. Теперь рассчитаю балку с измененным сечением, путем изменения ширины поясов по длине.
Сечение составной балки, подобранное по максимальному изгибающему моменту, можно уменьшить в местах снижения моментов (у опор). Однако каждое изменение сечения, дающее экономию металла, несколько увеличивает трудоемкость изготовления балки, и поэтому оно экономически целесообразно для балок пролетом более 12 м, что справедливо для нашего случая (16 м).
При равномерной нагрузке наивыгоднейшее по расходу стали место изменения сечения поясов однопролетной сварной балки находится на расстоянии примерно l
/6 пролета балки от опоры:  м. м.
Определим момент и поперечную силу в месте изменения сечения 1-1:
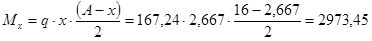 кН×м = 297345 кН×см; кН×м = 297345 кН×см;
 кН. кН.
Производимый подбор измененного сечения ведем по упругой стадии работы материала. Определим требуемый момент сопротивления и момент инерции измененного сечения исходя из прочности сварного стыкового шва, работающего на растяжение:
 см3
; см3
;
где Rwy
= 0,85·R = 0,85·23 = 19,55
 см4
. см4
.
Определим требуемый момент поясов, учитывая то, что момент инерции стенки остался тем же:
 см4
. см4
.
Требуемая площадь сечения поясов балки:
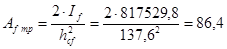 см2
. см2
.
Находим требуемое значение ширины пояса:
 см. см.
Окончательно примем bf
x
= 360 мм.
Принимаем пояса из универсальной стали 360х24 мм

Принятый пояс удовлетворяет условиям:
 . .
Проверим на прочность подобранное сечение балки. Определим момент инерции балки:
 см4
. см4
.
Определим момент сопротивления балки:
 см3
. см3
.
Тогда
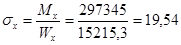 кН/см2
< 23×1 = 23 кН/см2
, кН/см2
< 23×1 = 23 кН/см2
,
Следовательно выбранная балка проходит по нормальному напряжению в месте изменения сечения.
3.2. Проверка прочности и общей устойчивости главной балки
3.2.1 Проведем проверку прочности балки
Проверка максимального нормального напряжения в середине балки и в месте изменения сечения была выполнена выше.
Проверим максимальное касательное напряжение в стенке на нейтральной оси сечения около опоры балки:
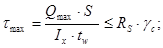
где S-статический момент полусечения балки
 см3
. см3
.
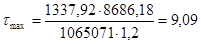 кН/см2
< 13,3×1 = RS
×gc
. кН/см2
< 13,3×1 = RS
×gc
.
Проверим местные напряжения в стенке под балками настила:
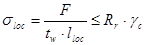 , ,
где F – расчетные значения опорных реакций балок настила:
 , ,
где q=72,63 кН/м – расчетная нагрузка на балку настила c учетом собственного веса балки;
а = 0,9 – шаг балок настила,
lloc
– длина передачи нагрузки на стенку главной балки:
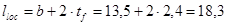 см. см.
 кН/см2
< Ry
×gc
= 23 кН/см2
. кН/см2
< Ry
×gc
= 23 кН/см2
.
Наличие местных напряжений, действующих на стенку балки, требует проверки совместного действия нормальных, касательных и местных напряжений на уровне поясного шва и под балкой настила по уменьшенному сечению вблизи места изменения сечения пояса. В рассматриваемом примере такого места нет, так как под ближайшей балкой настила будет стоять ребро жесткости, которое воспринимает давление балок настила, и передачи локального давления на стенку в этом месте не будет. Поэтому проверяем приведенные напряжения в месте изменения сечения 1-1 балки (где они будут максимальны) по формуле:
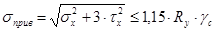 , ,
где
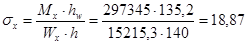 кН/см2
, кН/см2
,
 кН/см2 кН/см2
где
 см3
, см3
,
тогда, получим
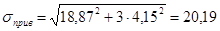 кН/см2 кН/см2
 кН/см2
. кН/см2
.
Из этих проверок следует, что прочность балки обеспечена.
3.2.2 Проверяем общую устойчивость балки
Проверим общую устойчивость в месте действия максимальных нормальных напряжений, принимая за расчетный пролет lef
= 90 см - расстояние между балками настила. Условие устойчивости записывается в виде:
 , ,
где lef
– расчетная длина балки между связями, препятствующими поперечным смещениям сжатого пояса балки;
bf
– ширина сжатого пояса (ширина полки);
tf
– толщина сжатого пояса (толщина полки);
hef
– расстояние (высота) между осями поясных листов.
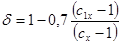
Условия применения уравнения устойчивости плоской формы изгиба:
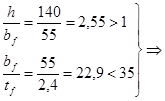 применение формулы возможно. применение формулы возможно.
При t=0 и с1х
=сх
получаем 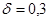
 . .
Проверим общую устойчивость в месте уменьшенного сечения главной балки (балка работает упруго и ): ):
 . .
Обе проверки показали, что общая устойчивость балки обеспечина.
3.2.3 Проверка прогиба
Проверку главной балки по второму предельному состоянию (проверку прогиба) производить нет надобности, так как принятая высота балки h
=
140 см >  см. см.
3.3 Проверка местной устойчивости сжатого пояса и стенки сварной балки
3.3.1 Проверка устойчивости сжатого пояса
Эту проверка производится в месте возникновения максимальных нормальных напряжений – в середине пролета главной балки.
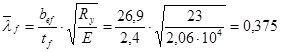
где bef
– расстояние от грани стенки до края поясного листа – полки:
 - свес пояса - свес пояса
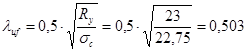
Поскольку  < < 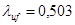 , то можно считать, что местная устойчивость сжатой полки балки обеспечена. , то можно считать, что местная устойчивость сжатой полки балки обеспечена.
3.3.2 Проверка устойчивости стенки
Определим необходимость укрепления стенки поперечными ребрами жесткости по п. 7.10 СНиПа II-23-81*. Так по СНиПу II-23-81* стенки балок следует укреплять поперечными ребрами жесткости, если значение условной гибкости стенки балки`lw
превышает 2,2.
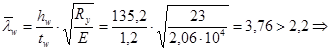 поперечные ребра жесткости необходимы. Кроме того, в зоне учета пластических деформаций необходима постановка ребер жесткости под каждой балкой настила, так как местные напряжения в стенке в этой зоне недопустимы. поперечные ребра жесткости необходимы. Кроме того, в зоне учета пластических деформаций необходима постановка ребер жесткости под каждой балкой настила, так как местные напряжения в стенке в этой зоне недопустимы.
Определим длину зоны использования пластических деформаций в стенке:
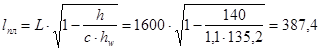 см, см,
т.е. по 1937 мм с каждой стороны от оси симметрии.
Расстановку вертикальных ребер жесткости принимаем согласно рисунку на стр. 30, через промежуток а = 270 см. Это расстояние удовлетворяет условию СНиПа II-23-81* (п. 7.10), которое между основными поперечными ребрами не должно превышать 2·hw
, т.к.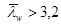
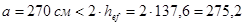 см. см.
По п. 7.3 СНиП II-23-81, так как`lw
= 3,76 > 2,5, то проверка устойчивости стенок обязательна. Проверку будем вести по п. 7.4 – 7.6 СНиПа II-23-81*.

Расстановка поперечных ребер жесткости главной балки, сечения проверки устойчивости стенки.
Проверим местную устойчивость стенки в сечении 2-2, для этого определяем средние значения M2
и Q2
на расстоянии х2
= 395 см от опоры (под балкой настила), что почти совпадает с рекомендацией расстояния в  от края отсека. от края отсека.
В этом сечении возникают следующие усилия:
 кНм, кНм,
 кН. кН.
И соответствующие этим усилиям напряжения будут равны:
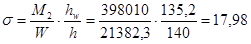 кН/см2
, кН/см2
,
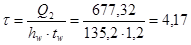 кН/см2
. кН/см2
.
Проверим местные напряжения в стенке под балками настила:
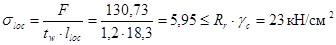 , ,
Определяем критические напряжения:
 , ,
Где 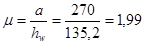 , , 
 кН/см2
. кН/см2
.
Размеры отсека 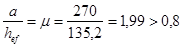 и и 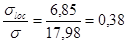
Предельное значение этого отношения находим по табл. 24 СНиПа II-23-81*, в зависимости от значения коэффициента d, учитывающего степень упругого защемления стенки в поясах:
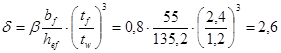 , ,
где b = 0,8, коэффициент принимаемый по табл. 22 СНиПа II-23-81*;
Тогда  . .
Расчет на местную устойчивость стенки будем проводить по п. 7.6. в
СНиПа II-23-81*.
Критические нормальные напряжения:
 кН/см2
; кН/см2
;
Определяем  , подставляя вместо а
значение а/2
: , подставляя вместо а
значение а/2
:
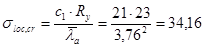 кН/см2
, кН/см2
,
где  . .
С учетом этого, по формуле (79) СНиПа II-23-81* получим:

 . .
Проверка показала, что устойчивость стенки обеспечена и постановка ребер жесткости на расстоянии 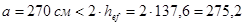 см возможна. см возможна.
Помимо проверки устойчивости стенки в области больших нормальных напряжений необходимо также проверить ее устойчивость и в области больших касательных напряжений - вблизи от опоры балки. Проверим на устойчивость стенки в сечении 3-3, для этого определяем средние значения M3
и Q3
на расстоянии х3
= 125 см от опоры (под балкой настила), что почти совпадает с рекомендацией расстояния в  от края отсека. от края отсека.
В этом сечении возникают следующие усилия:
 кНм, кНм,
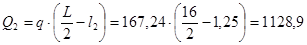 кН. кН.
И соответствующие этим усилиям напряжения будут равны:
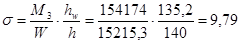 кН/см2
, кН/см2
,
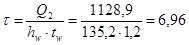 кН/см2
. кН/см2
.
Проверим местные напряжения в стенке под балками настила:
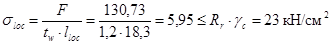 , ,
Определяем критические напряжения:
 , ,
Где 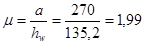 , , 
 кН/см2
. кН/см2
.
Размеры отсека 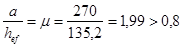 и и 
Предельное значение этого отношения находим по табл. 24 СНиПа II-23-81.
 , ,
Тогда  . .
Расчет на местную устойчивость стенки будем проводить по п. 7.6. в
СНиПа II-23-81*.
Критические нормальные напряжения:
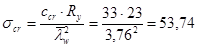 кН/см2
; кН/см2
;
Определяем  , подставляя вместо а
значение а/2
: , подставляя вместо а
значение а/2
:
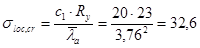 кН/см2
, кН/см2
,
где  . .
С учетом этого, по формуле (79) СНиПа II-23-81* получим:
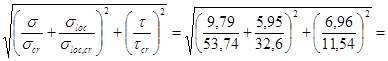
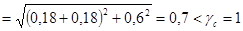 . .
Обе проверки показали, что запроектированная балка удовлетворяет требованиям прочности, прогиба, общей и местной устойчивости.
3.4 Расчет поясных швов главной балки
Так как балка работает с учетом пластических деформаций, то швы выполняем двухсторонние, автоматической сваркой в лодочку, сварной проволокой Св-08А.
Катет шва определим под первой от опоры балкой настила, где сдвигающая сила максимальна, то есть в сечении х = 25 см.
Рассчитывать катет будем по формуле:
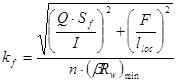 , ,
где n = 1 при односторонних швах, n = 2 при двухсторонних швах;
(bRw
)min
– произведение глубины проплавления на расчетное сопротивление для расчетного сечения.
Из пункта 3.2.1 возьмем уже рассчитанные величины:
Iх
= 1065071 см4
; Sf
х
= 5944,32 cм3
; F = 150,52 кН; lloc
= 18,3 см.
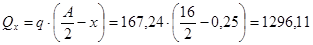 кН; кН;
По табл. 4 СНиП II-23-81* определим значение нормативного сопротивления металла шва по временному сопротивлению Rwun
= 41 кН/см2
. Тогда согласно табл. 4 СНиП II-23-81* расчетное сопротивление углового шва условному срезу по металлу шва:
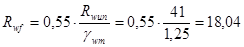 кН/см2
, кН/см2
,
где gwm
= 1,25, - коэффициент надежности по материалу шва.
По табл. 51 СНиП II-23-81* для стали С255 определим временное сопротивление стали разрыву Run
= 37 кН/см2
. Тогда согласно СНиП II-23-81* расчетное сопротивление углового шва условному срезу по металлу границы сплавления:
 кН/см2
. кН/см2
.
По табл. 34 СНиП II-23-81* для выбранного типа сварки примем соответствующие коэффициенты для расчета углового шва:
bf
= 1,1 – по металлу шва;
bz
= 1,15 – по металлу границы сплавления.
Определим, какое сечение в соединении является расчетным (более опасное):
 кН/см2
, Þ расчетным является сечение по металлу границы сплавления. кН/см2
, Þ расчетным является сечение по металлу границы сплавления.
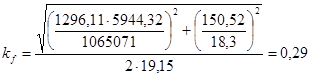 см. см.
По табл. 38 СНиП II-23-81* для пояса толщиной 24 мм принимаем катет шва, равный минимальному kf
= 7 мм, что больше, получившегося по расчету – 2,9 мм.
3.5 Расчет опорного ребра главной балки
Размеры опорных ребер определим из расчета на смятие торца ребра:
 , ,
где F - опорная реакция балки N (будет равна значению поперечной силы на торце балки, найденной в пункте 3):
 кН; кН;
Rp
– расчетное сопротивление смятию торцевой поверхности, по табл. 1 СНиПа II-23-81* находим:
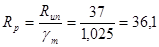 кН/см2
, кН/см2
,
где по табл. 51 СНиП II-23-81* для стали С255 определим временное сопротивление стали разрыву Run
= 37 кН/см2
; по табл. 2* СНиП II-23-81* для стали по ГОСТу 27772-88, находим, что коэффициент надежности по материалу gm
= 1,025.
Найдем требуемую площадь опорного ребра:
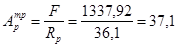 см2
. см2
.
Уже принятая ширина пояса bfx
= 36 cм, следовательно толщину ребра определим, как
 см, см,
принимая окончательно tp
= 12 мм.
Тогда
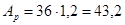 см2 см2
 см2
, см2
,
сечение подобранного торца балки проходит проверку на смятие.
Проверим опорный участок балки на устойчивость из плоскости балки, как условного опорного стержня, включающего в площадь своего сечения опорные ребра и часть стенки балки шириной bw
.
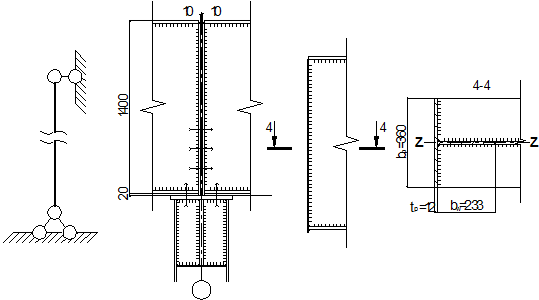
Расчетная схема на устойчивость опорного участка главной балки
 см. см.
Площадь расчетного сечения опорной части балки:
 см2
. см2
.
Момент инерции сечения относительно оси z-z:
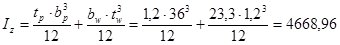 см4
. см4
.
Радиус инерции сечения:
 см. см.
Гибкость:
 . .
Условная гибкость:
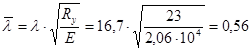 . .
Условие устойчивости можно записать в виде:
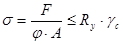 , ,
где j = 0,97025 - коэффициент продольного изгиба балки (по табл. 72 СНиПа II-23-81*),
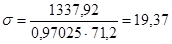 кН/см2
< Ry
×gc
= 23 кН/см2
, кН/см2
< Ry
×gc
= 23 кН/см2
,
то есть принятая опорная стойка главной балки устойчива.
Рассчитаем прикрепление опорного ребра к стенке балки двухсторонними швами с помощью полуавтоматической сварки проволокой Св-08А при вертикальном расположении шва.
Согласно табл. 4 СНиП II-23-81* расчетное сопротивление углового шва условному срезу по металлу шва:
 кН/см2
, кН/см2
,
где gwm
= 1,25, - коэффициент надежности по материалу шва.
По СНиП II-23-81* расчетное сопротивление углового шва условному срезу по металлу границы сплавления:
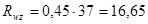 кН/см2
. кН/см2
.
По табл. 34 СНиП II-23-81 для выбранного типа сварки примем соответствующие коэффициенты для расчета углового шва:
bf
= 0,9 – по металлу шва;
bz
= 1,05 – по металлу границы сплавления.
Определим, какое сечение в соединении является расчетным:
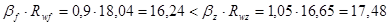 кН/см2
, Þ расчетным является сечение по металлу шва. кН/см2
, Þ расчетным является сечение по металлу шва.
Определим катет сварных швов:
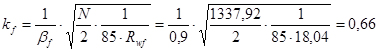 см. см.
Полученное значение катета шва больше минимального kf
min
= 5 мм, поэтому окончательно принимаем kf
= 7 мм.
Проверяем длину рабочей части шва
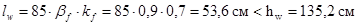
Ребро привариваем к стенке по всей высоте сплошными швами.
3.6 Проектирование стыка главной балки на высокопрочных болтах
Очевидно, что стык необходим по середине балки, где Мmax
= 535168 кН·см и Q = 0.
По табл. 61 СНиП II-23-81* выбираем высокопрочные болты для соединения в = 24 мм из стали 40Х "селект" с наименьшим временным сопротивлением Rbun
= 110 кН/см2
и площадью сечения болта нетто Abn
= 3,52 см2
(табл. 62). По табл. 36 СНиП II-23-81* определяем, что при газопламенной обработке соединяемых поверхностей и при регулировании натяжения болтов по моменту коэффициент трения m = 0,42, коэффициент надежности gh
= 1,12 (при разности номинальных диаметров отверстий и болтов в = 1 – 4).
Расчетное усилие, которое может быть воспринято каждой поверхностью трения соединяемых элементов, стянутых одним высокопрочным болтом, определим по формуле
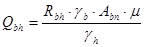 , ,
где Rbh
– расчетное сопротивление высокопрочного болта, принимаемое по формуле (3) в СНиПе II-23-81*:
 кН/см2
; кН/см2
;
gb
= 1,0 (при количестве болтов больше 10) коэффициент условий работы соединения.
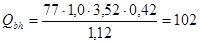 кН. кН.
Стык поясов
Перекрещиваем тремя накладками каждый пояс балки сечением 550´14 мм и 2´260´14 мм. Общая площадь сечения
 см2
> 55·2,4 = 132 см2
. см2
> 55·2,4 = 132 см2
.
Определим усилие в поясе:
 кН. кН.
Количество высокопрочных болтов в соединении стыков поясов:
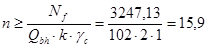 , ,
принимаем n = 18 болтов и размещаем их согласно рис. на стр. 40.
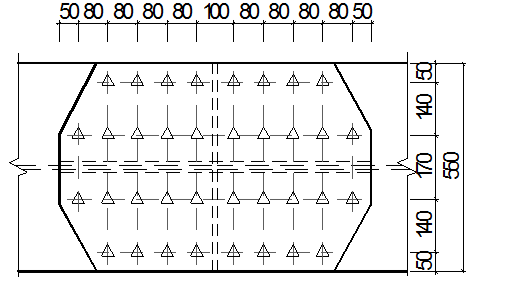
Размещение высокопрочных болтов на стыке поясов главной балки.
Стык стенки.
Стенку перекрываем двумя вертикальными накладками сечением 360´1300´10 мм.
Момент, действующий на стенку:
 кН·см. кН·см.
Расстояние между крайними по высоте рядами болтов принимаем:
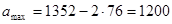 мм. мм.
Вычислим коэффициент стыка a:
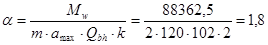 , ,
где m – число вертикальных рядов болтов на полунакладке.
Определяем, что число рядов болтов по вертикали равно 9, что соответствует шагу рядов болтов по высоте 150 мм (8´150 = 1200 мм).
Проверим стык стенки по формуле:
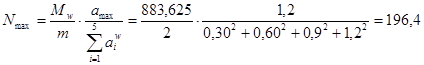 кН < Qbh
·k = 204 кН. кН < Qbh
·k = 204 кН.

Размещение высокопрочных болтов на стыке стенки главной балки.
Проверим ослабление нижнего растянутого пояса отверстиями под болты диаметром do
= 26 мм (на 2 мм больше диаметра болта).
Пояс ослаблен двумя отверстиями по краю стыка, поэтому площадь сечения пояса нетто:
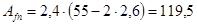 см2
, см2
,
а площадь сечения пояса брутто:
 см2
. см2
.
Согласно п.11.14 СНиПа II-23-81*:
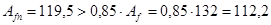 см2
, см2
,
то есть ослабление пояса можно не учитывать.
Проверим ослабление накладок в середине стыка четырьмя отверстиями:
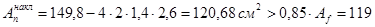 см2
, см2
,
следовательно, ослабление накладок можно не учитывать.
3.7 Проектирование сварного стыка главной балки
На монтаже сжатый пояс и стенку всегда соединяют прямым швом встык, а растянутый пояс – косым швом под углом 600
, так как при монтаже автоматическая сварка и повышенные способы контроля затруднены. Такой стык будет равнопрочен основному сечению балки и по этому не рассчитывается.
 Чтобы уменьшить сварочные напряжения, сначала сваривают поперечные стыковые швы стенки 1
и поясов 2
и 3
, имеющие наибольшую поперечную усадку. Оставленные не заваренными на заводе участки поясных швов длиной около 500 мм дают возможность поясным листам несколько вытянуться при усадке швов 2
и 3
. Последним заваривают угловые швы 4
и 5
, имеющие небольшую продольную усадку. Чтобы уменьшить сварочные напряжения, сначала сваривают поперечные стыковые швы стенки 1
и поясов 2
и 3
, имеющие наибольшую поперечную усадку. Оставленные не заваренными на заводе участки поясных швов длиной около 500 мм дают возможность поясным листам несколько вытянуться при усадке швов 2
и 3
. Последним заваривают угловые швы 4
и 5
, имеющие небольшую продольную усадку.
4. Проектирование и расчет колонн
4.1 Расчетная схема и расчетная длина колонны
В качестве расчетной схемы выберем колонну, шарнирно закрепленную с двух сторон. Найдем фактическую длину колонны l, при высоте фундамента 500 мм:
 мм. мм.
Расчетная длина колонны равна:  см. см.
где m - коэффициент расчетный длины, определяется по табл. 71,а СНиПа II-23-81*.
 Расчетная схема центрально-сжатого стержня колонны. Расчетная схема центрально-сжатого стержня колонны.
4.2 Определение продольной силы в колонне, выбор типа сечения колонны
Опорная реакция в главной балке равна Q
= 1337,92 кН, а продольная сила в колонне равна
N
= 2×1337,92+0,8·lk
= 3299,36 кН, используем колонну сплошного типа сечения. Примем, что сечение будет двутавровым, сваренным из трех листов.
4.3 Подбор сечения, проверка общей устойчивости колонн и местной устойчивости стенки и полок
Материал колонн – сталь С275. Для нее по табл. 51 СНиПа II-23-81* определим, что для t
до 20 мм расчетное сопротивление растяжению, сжатию и изгибу по пределу текучести Ry
= 26 кН/см2
.
По формуле 7 СНиПа II-23-81* имеем, что 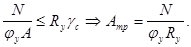 Найдем Найдем 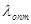 по формуле: по формуле:
 Примем l
= 71, тогда j
= 0,739, Примем l
= 71, тогда j
= 0,739,
 см2
. см2
.
Т.к. 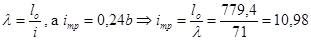 см см 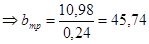 см, примем bf
= 460 мм, hw
= 560 мм. см, примем bf
= 460 мм, hw
= 560 мм.
Для того, чтобы воспользоваться формулой пункта 7.14 СНиП II-23-81*, определим значение
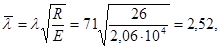 тогда согласно табл. 27 СНиП II-23-81* получим, что: тогда согласно табл. 27 СНиП II-23-81* получим, что:
 см,принимаем tw
= 9 мм. см,принимаем tw
= 9 мм.
Тогда 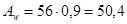 см2
, необходимая площадь поясов равна: см2
, необходимая площадь поясов равна:
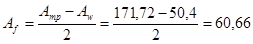 см2
, Þ см2
, Þ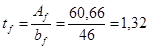 см, см,
принимаем 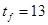 мм. мм.
Проверим местную устойчивость полки колонны по табл.29 СНиП II-23-81*:
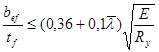 , ,
где  , т.к. , т.к.
 см2
, см2
,
 см4
, Þ см4
, Þ
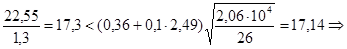 местная устойчивость полки не обеспечена. местная устойчивость полки не обеспечена.
Увеличиваем 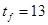 до до  мм. мм.
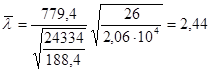 , т.к. , т.к.
 см2
, см2
,
 см4
, Þ см4
, Þ
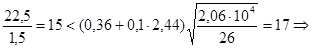 местная устойчивость полки обеспечена. местная устойчивость полки обеспечена.
Проверяем напряжение по подобранному сечению:

Подобранное сечение удовлетворяет требованиям общей устойчивости.
Сечение колонны со сплошной стенкой

Проверим местную устойчивость стенки колонны. Стенка колонны устойчива, если условная гибкость стенки 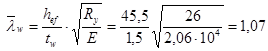 меньше или равна предельной условной гибкости меньше или равна предельной условной гибкости  , т.к. 1,07 < 1,47 Þ стенка устойчива. , т.к. 1,07 < 1,47 Þ стенка устойчива.
4.4. Расчет и конструирование оголовка колонны
На колонну со сплошной стенкой свободно сверху опираются балки. Усилие на стержень колонны передается опорными ребрами балок через плиту оголовка. Ширина опорных ребер балок bp
= 360 мм. На колонну действует продольная сила N= 2678 кН. Торец колонны фрезерован. Толщину плиты оголовка принимаем равной tf
= 25 мм.
Плита поддерживается ребрами, приваренными к стенке колонны. Толщину ребер определяем из условия смятия. Требуемая площадь смятия:

 Определим высоту ребра, исходя из длины швов, прикрепляющих ребро к стенке. Определим высоту ребра, исходя из длины швов, прикрепляющих ребро к стенке.
Задаемся катетом шва kf
= 10 мм.
Сварные швы будем выполнять полуавтоматической сваркой электродами Э42, выполненными из проволоки сплошного сечения Св-08А со значением
Схема опирания главной балки на колонну
 кН/см2
. Для стали С275 значение кН/см2
. Для стали С275 значение  кН/см2
. Таким образом, расчетные сопротивления сварного шва по металлу шва и по границе сплавления соответственно будут равны ( по табл.3 СНиП II-23-81*): кН/см2
. Таким образом, расчетные сопротивления сварного шва по металлу шва и по границе сплавления соответственно будут равны ( по табл.3 СНиП II-23-81*):
 кН/см2
, кН/см2
,
 кН/см2
. кН/см2
.
Значения коэффициентов  при сварке в нижнем положении равны: при сварке в нижнем положении равны: 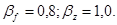
 кН/см2
, кН/см2
,
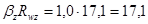 кН/см2
, следовательно, необходимо рассчитать сварной шов на условный срез по металлу границы сплавления. Тогда длина одного углового шва будет равна кН/см2
, следовательно, необходимо рассчитать сварной шов на условный срез по металлу границы сплавления. Тогда длина одного углового шва будет равна
( при kf
= 10 мм – для вставки стенки в колонну > 10 мм.)
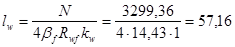 см, принимаем hp
=lw
+1=57,16+1=58 см. см, принимаем hp
=lw
+1=57,16+1=58 см.
Толщину вставки в стенку колонны определим из расчета стенки на срез:
 см, принимаем tw
, вс
= 19 мм. см, принимаем tw
, вс
= 19 мм.
4.5 Расчет и конструирование базы колонны
Собственный вес колонны:
 кг. кг.
Расчетная нагрузка на базу колонны:
 кН. кН.
Требуемая площадь плиты базы колонны
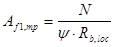 , ,
где y - коэффициент, зависящий от характера распределения местной нагрузки по площади смятия, при равномерно распределенной нагрузке y = 1;
Rb
,
loc
– расчетное сопротивление смятию:
 , ,
где Rb
– расчетное сопротивление тяжелого, мелкозернистого и легкого бетонов для предельных состояний первой группы на осевое сжатие, для бетона класса В12,5 Rb
= 0,75 кН/см2
;
a - коэффициент для расчета на изгиб, зависящий от характера операния плит, для бетонов класса ниже В25 a =1;
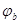 - принимают не более 2,5 для бетонов класса выше В 7,5, потому в нашем случае j
b
= 2. - принимают не более 2,5 для бетонов класса выше В 7,5, потому в нашем случае j
b
= 2.
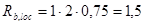 кН/см2
. кН/см2
.
При центрально-сжатой колонне и значительной жесткости плиты напряжения под плитой в бетоне можно считать равномерно распределенными, поэтому y = 1, тогда
 см2
. см2
.
Считая в первом приближении плиту базы квадратной, будем иметь стороны плиты равными
 см; см;
принимаем размеры плиты 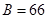 см, L = 75 cм (по конструктивным соображениям), тогда см, L = 75 cм (по конструктивным соображениям), тогда
 см2
. см2
.
Напряжение под плитой
 кН/см2
. кН/см2
.
Плита работает на изгиб, как пластинка, опертая на соответствующее число кантов (сторон). Нагрузкой является отпор фундамента. В плите имеются три участка.
На участке 1
плита работает по схеме "пластинка, опертая на четыре канта". Соотношение сторон
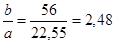 > 2, > 2,
то есть плиту можно рассматривать как однопролетную балочную, свободно лежащую на двух опорах.
Изгибающий момент:
 кН×см. кН×см.
Требуемая толщина плиты подбирается по максимальному изгибающему моменту, принимая материал плиты – сталь С275, для которой расчетное сопротивление Ry
= 26 кН/см2
, тогда
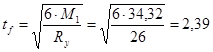 см, см,
принимаем толщину базы 24 мм.
На участке 2
плита работает тоже, как пластинка, опертая на три канта.
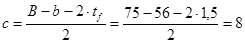 см, см,
Соотношение сторон
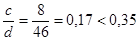 , ,
следовательно плиту можно рассматривать как консоль длиной с.
Изгибающий момент:
 кН×см. кН×см.
На участке 3
плита оперта на три канта.
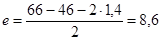 см, см,
 , ,
следовательно плиту можно рассматривать как консоль длиной е.
Изгибающий момент:
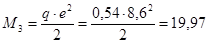 кН×см. кН×см.
 База колонны
(цифры в кружках - номера участков) База колонны
(цифры в кружках - номера участков)
Расчет траверсы.
Считаем в запас прочности, что усилие на плиту передается только через швы, прикрепляющие ствол колонны к траверсам и не учитываем швы, соединяющие ствол колонны непосредственно с плитой базы. Траверса работает на изгиб, как балка с двумя консолями. Высота траверсы определяется из условия прочности сварного соединения траверсы с колонной.
Рассчитаем угловые швы на условный срез.
Задаемся катетом шва kf
= 13 мм.
Сварные швы будем выполнять полуавтоматической сваркой электродами Э42, выполненными из проволоки сплошного сечения Св-08А со значением  кН/см2
. Для стали С275 значение кН/см2
. Для стали С275 значение  кН/см2
. Таким образом, расчетные сопротивления сварного шва по металлу шва и по границе сплавления соответственно будут равны ( по табл.3 СНиП II-23-81*): кН/см2
. Таким образом, расчетные сопротивления сварного шва по металлу шва и по границе сплавления соответственно будут равны ( по табл.3 СНиП II-23-81*):
 кН/см2
, кН/см2
,
 кН/см2
. кН/см2
.
Значения коэффициентов  при сварке в нижнем положении равны: при сварке в нижнем положении равны: 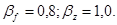
 кН/см2
, кН/см2
,
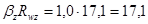 кН/см2
, следовательно, необходимо рассчитать сварной шов на условный срез по металлу границы сплавления. Тогда длина одного углового шва будет равна кН/см2
, следовательно, необходимо рассчитать сварной шов на условный срез по металлу границы сплавления. Тогда длина одного углового шва будет равна
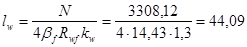 см, см,
Высота траверсы h
т
= lw
+1 = 44,09+1 = 45,09 см, принимаем h
т
= 45 см.
Список используемой литературы
1. Металлические конструкции. Под редакцией Г.С. Веденикова, Стройиздат, 1998.
2. Металлические конструкции. Под редакцией Е.И. Беленя, М., Стройиздат, 1986.
3. СНиП II-23-81*. Стальные конструкции (Госстрой СССР. – М. ЦИТП Госстроя СССР, 1996)
|