КУРСОВАЯ РАБОТА
"Неразрешимость логики первого порядка"
формальный неразрешимость логика остановка
Философы сформулировали наиболее важные идеи искусственного интеллекта, но для преобразования его в формальную науку потребовалось достичь определенного уровня математической формализации в трех фундаментальных областях: логика, вычисления и вероятность.
Истоки идей формальной логики можно найти в работах философов древней Греции, но ее становление как математической дисциплины фактически началась с трудов Джорджа Буля (1815–1864), который детально разработал логику высказываний, или булеву логику. В 1879 году Готтлоб Фреге (1848–1925) расширил булеву логику для включения в нее объектов и отношений, создав логику первого порядка, которая в настоящее время используется как наиболее фундаментальная система представления знаний.
Одним из принципиально важных результатов математической логики является доказательство неразрешимости в логике первого порядка распознавания проблем как общезначимости, так и выполнимости ее предложений.
Цель исследования – изучить доказательства неразрешимости логики первого порядка. Для достижения данной цели необходимо выделить ряд задач:
1. Изучить основные понятия логики первого порядка.
2. Рассмотреть понятие машины Тьюринга и доказать неразрешимость проблемы остановки.
3. Вывести неразрешимость логики первого порядка из неразрешимости проблемы остановки.
4. Разобрать доказательство неразрешимости логики первого порядка методом Геделя.
1. Понятие формальной системы
Формальная система (или формальная теория) – результат строгой формализации теории, предполагающей полную абстракцию от смысла слов используемого языка, причем все условия, регулирующие употребление этих слов в теории, явно высказаны посредством аксиом и правил, позволяющих вывести одну фразу из других.
Формальная теория считается определенной
, если:
- задано конечное или счётное множество произвольных символов (конечные последовательности символов называются выражениями теории);
- имеется подмножество выражений, называемых формулами;
- выделено подмножество формул, называемых аксиомами;
- имеется конечное множество отношений между формулами, называемых правилами вывода.
Обычно имеется эффективная процедура, позволяющая по данному выражению определить, является ли оно формулой. Часто множество формул задаётся индуктивным определением. Как правило, это множество бесконечно. Множество символов и множество формул в совокупности определяют язык или сигнатуру формальной теории.
Чаще всего имеется возможность эффективно выяснять, является ли данная формула аксиомой; в таком случае теория называется эффективно аксиоматизированной или аксиоматической. Множество аксиом может быть конечным или бесконечным. Если множество аксиом бесконечно, то, как правило, оно задаётся с помощью конечного числа схем аксиом и правил порождения конкретных аксиом из схемы аксиом. Обычно аксиомы делятся на два вида: логические аксиомы (общие для целого класса формальных теорий) и нелогические или собственные аксиомы (определяющие специфику и содержание конкретной теории).
Для каждого правила вывода R и для каждой формулы A эффективно решается вопрос о том, находится ли выбранный набор формул в отношенни R с формулой A, и если да, то A называется непосредственным следствием данных формул по правилу R.
Выводом
называется всякая последовательность формул такая, что всякая формула последовательности есть либо аксиома, либо непосредственное следствие каких-либо предыдущих формул по одному из правил вывода.
Формула называется теоремой
, если существует вывод, в котором эта формула является последней.
Теория, для которой существует эффективный алгоритм, позволяющий узнавать по данной формуле, существует ли ее вывод, называется разрешимой
; в противном случае теория называется неразрешимой.
Теория, в которой не все формулы являются теоремами, называется абсолютно непротиворечивой
.
Дедуктивная теория считается заданной
, если:
– задан алфавит (множество) и правила образования выражений (слов) в этом алфавите;
– заданы правила образования формул (правильно построенных, корректных выражений);
– из множества формул некоторым способом выделено подмножество T теорем (доказуемых формул).
Свойства дедуктивных теорий:
1. Противоречивость
. Теория, в которой множество теорем покрывает всё множество формул (все формулы являются теоремами, «истинными высказываниями»), называется противоречивой. В противном случае теория называется непротиворечивой. Выяснение противоречивости теории – одна из важнейших и иногда сложнейших задач формальной логики. После выяснения противоречивости теория, как правило, не имеет дальнейшего ни теоретического, ни практического применения.
2. Полнота
. Теория называется полной, если в ней для любой формулы F выводима либо сама F, либо ее отрицание. В противном случае, теория содержит недоказуемые утверждения (утверждения, которые нельзя ни доказать, ни опровергнуть средствами самой теории), и называется неполной.
3. Независимость аксиом
. Отдельная аксиома теории считается независимой, если эту аксиому нельзя вывести из остальных аксиом. Зависимая аксиома по сути избыточна, и ее удаление из системы аксиом никак не отразится на теории. Вся система аксиом теории называется независимой, если каждая аксиома в ней независима.
4. Разрешимость
. Теория называется разрешимой, если в ней понятие теоремы эффективно, то есть существует эффективный процесс (алгоритм), позволяющий для любой формулы за конечное число шагов определить, является она теоремой или нет.
Логика первого порядка (исчисление предикатов) – формальное исчисление, то есть это совокупность абстрактных объектов, не связанных с внешним миром, в котором представлены правила оперирования множеством символов в строго синтаксической трактовке без учета смыслового содержания.
Язык
логики первого порядка
строится на основе сигнатуры, состоящей из следующих символов:
1) логические
– символы логических операций ¬,  , , 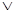 , ↔, →; , ↔, →;
– символы кванторных операций ", $;
– служебные символы: скобки и запятая.
2) нелогические
– множество предикатных символов, с которым связана арность, то есть число возможных аргументов P(
n
)
, Q(
m
)
, …, P1
(
n
)
, P2
(
n
)
;
– символы пропозициональных переменных X, Y, Z, …, X1
, X2
, … (можно считать, что символы пропозициональных переменных – это нульместные предикатные символы);
– символы предметных переменных x, y, z, …, x1
, x2
,…;
– символы предметных констант a
, b
, c
, …, a
1
, a
2
, …
n
-местным предикатом
P (x1, x2,…, xn) называется функция P: M1
ЧM2
Ч…ЧMn
→ {1,0}, определенная на наборах длины n элементов некоторого множества M= M1
ЧM2
Ч…ЧMn
и принимающая значения в области {1,0}. Множество М называется предметной областью предиката, его элементы – предметными константами.
Отрицанием
предиката P(x1
, x2
,…, xn
), определенного на множестве M1
ЧM2
Ч…ЧMn
называется предикат ¬P(x1
, x2
,…, xn
), определенный на том же множестве, который на наборе (a
1
, a
2
,…, a
n
)  M1
ЧM2
Ч…ЧMn M1
ЧM2
Ч…ЧMn

Конъюнкцией
предикатов P(x1
, x2
,…, xn
), определенного на множестве M1
ЧM2
Ч…ЧMn
, и Q(y1
, y2
,…, ym
), определенного на множестве N1
ЧN2
Ч…ЧNm
, называется предикат P Q(x1
, x2
,…, xn
, y1, y2,…, ym) c пердметной областью M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn
, который на наборе (a
1
, a
2
,…, a
n
, b
1
, b
2
,…, b
m
) Q(x1
, x2
,…, xn
, y1, y2,…, ym) c пердметной областью M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn
, который на наборе (a
1
, a
2
,…, a
n
, b
1
, b
2
,…, b
m
)  M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn

Дизъюнкцией предикатов
P(x1
, x2
,…, xn
), определенного на множестве M1
ЧM2
Ч…ЧMn
, и Q(y1
, y2
,…, ym
), определенного на множестве N1
ЧN2
Ч…ЧNm
, называется предикат P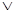 Q(x1
, x2
,…, xn
, y1, y2,…, yn) c пердметной областью M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn
, который на наборе (a
1
, a
2
,…, a
n
, b
1
, b
2
,…, b
m
) Q(x1
, x2
,…, xn
, y1, y2,…, yn) c пердметной областью M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn
, который на наборе (a
1
, a
2
,…, a
n
, b
1
, b
2
,…, b
m
)  M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn

Импликацией
предикатов P(x1
, x2
,…, xn
), определенного на множестве M1
ЧM2
Ч…ЧMn
, и Q(y1
, y2
,…, ym
), определенного на множестве N1
ЧN2
Ч…ЧNm
, называется предикат P → Q(x1
, x2
,…, xn
, y1, y2,…, yn) c пердметной областью M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn
, который на наборе (a
1
, a
2
,…, a
n
, b
1
, b
2
,…, b
m
)  M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn

Эквивалентностью
предикатов P(x1
, x2
,…, xn
), определенного на множестве M1
ЧM2
Ч…ЧMn
, и Q(y1
, y2
,…, ym
), определенного на множестве N1
ЧN2
Ч…ЧNm
, называется предикат P(x1
, x2
,…, xn
) ↔ Q (y1, y2,…, yn) c пердметной областью M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn
, который на наборе (a
1
, a
2
,…, a
n
, b
1
, b
2
,…, b
m
)  M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn M1
ЧM2
Ч…ЧMn
ЧN1
ЧN2
Ч…ЧNn
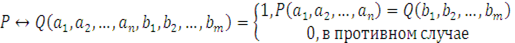
Операцией связывания
квантором общности
переменной xi в n-местном предикате P(x1
, x2
,…, xn
)), определенном на множестве M1
ЧM2
Ч…ЧMn
, называется операция, в результате которой получается n-1-местный предикат "xi
P(x1
, x2
,…, xi
-1
, xi
+1
,…, xn
), который при значениях x1
=
a
1
, …, xi
-1
= a
i
-1
, xi
-1
= a
i
-1
, …, xn
=
a
n
истинен, если при любых значениях xi
=
a
i
высказывание P(a
1
, a
2
,…, a
n
) истинно.
Операцией связывания квантором существования
переменной xi в n-местном предикате P(x1
, x2
,…, xn
) называется операция, в результате которой получается n-1-местный предикат $xi
P(x1
, x2
,…, xi
-1
, xi
+1
,…, xn
), который при значениях x1
=
a
1
, …, xi
-1
= a
i
-1
, xi
-1
= a
i
-1
, …, xn
=
a
n
истинен, если при некотором значении xi
=
a
i
высказывание P(a
1
, a
2
,…, a
n
) истинно.
Вхождение какой-либо переменной в формулу, называется свободным, если оно не входит в область действия никакого квантора по этой переменной.
Формулами
логики предикатов являются:
– всякая нульместная предикатная переменная;
– P(
n
)
(x1
, x2
,…, xn
), где P(
n
)
– n-местная предикатная переменная, а x1
, x2
,…, xn
– свободные переменные;
– 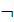 F, где F – формула; F, где F – формула;
– F1
 F2
, F1 F2
, F1
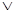 F2
, F1
↔ F2
, F1
→ F2
, где F1
и F2
– формулы, в которых общие переменные являются одновременно свободными или одновременно связанными; F2
, F1
↔ F2
, F1
→ F2
, где F1
и F2
– формулы, в которых общие переменные являются одновременно свободными или одновременно связанными;
– "xi
P(x1
, x2
,…, xi
-1
, xi
+1
,…, xn
) и $xi
P(x1
, x2
,…, xi
-1
, xi
+1
,…, xn
), где P(x1
, x2
,…, xn
) – формула, в которой xi
– свободная переменная
Определение истинности формул алгебры предикатов вводится с помощью интерпретации
. В классическом случае интерпретация определяется следующими данными
1) предметная область;
2) всякой предметной константе ставится в соответствие некоторый предмет, определенный в области;
3) каждому пропозициональному символу ставится в соответствие некоторое значение 1 (истина) или 0 (ложь);
4) каждому предикатному символу языка ставится в соответствие некоторая характеристическая функция.
Классификация формул:
Формула называется
а) выполнимой (опровержимой)
на множестве М
, если существует ее истинная (ложная) интерпретация на этом множестве;
б) тождественно-истинной (тождественно-ложной)
на множестве М, если любая ее интерпретации на этом на этом множестве истина (ложна);
в) выполнимой (опровержимой)
, если существует предметная область, на которой она выполнима (опровержима);
г) общезначимой (противоречием)
, если на любой предметной области она тождественно-истинная (тождественно-ложная).
Множеством истинности
предиката P(x1
, x2
,…, xn
), заданного на множестве M1
ЧM2
Ч…ЧMn
, называется совокупность всех упорядоченных систем (a
1
, a
2
,… a
n
), в которых a
1
е M1
a
2
е M2
,…, a
n
е Mn
, таких, что данный предикат обращается в истинное высказывание Р(a
1
, a
2
,… a
n
) при подстановке x1
= a
1
x2
= a
2
,…, xn
= a
n
.
Обозначается P+
.
Два n-местных предиката Р(x1
, x2
,…, xn
) и Q(x1
, x2
,…, xn
), заданных на одном и том же множестве M1
ЧM2
Ч…ЧMn
называются равносильными
, если набор предметов a
1
е M1
a
2
е M2
,…, a
n
е Mn
превращает первый предикат в истинное высказывание Р(a
1
, a
2
,… a
n
) тогда же, когда этот набор предметов превращает второй предикат в истинное. Переход от предиката Р(x1
, x2
,…, xn
) к равносильному ему предикату Q(x1
, x2
,…, xn
) называется равносильным преобразованием первого.
Предикат Р(x1
, x2
,…, xn
), заданный на множестве M1
ЧM2
Ч…ЧMn
называется следствием
предиката Q(x1
, x2
,…, xn
), если он превращается в истинное высказывание на всех тех наборах значений предметных переменных из соответствующих множеств, на которых в истинное высказывание превращается предикат Q(x1
, x2
,…, xn
).
3. Понятие машины Тьюринга
Машина Тьюринга есть математическая (воображаемая) машина, а не машина физическая. Она есть такой же математический объект, как функция, производная, интеграл, группа и т.д. И так же как и другие математические понятия, понятие машины Тьюринга отражает объективную реальность, моделирует некие реальные процессы.
Машины Тьюринга
– это совокупность следующих объектов
1) внешний алфавит A={a
0
,
a
1
, …,
a
n
};
2) внутренний алфавит Q={q
1
, q
2
,…, q
m
} – множество состояний;
3) множество управляющих символов {П, Л, С}
4) бесконечная в обе стороны лента, разделённая на ячейки, в каждую из которых в любой дискретный момент времени может быть записан только один символ из алфавита А;
5) управляющее устройство, способное находиться в одном из множества состояний
Символом пустой ячейки является буква внешнего алфавита а
0
.
Среди состояний выделяются два – начальное q
1
, находясь в котором машина начинает работать, и заключительное (или состояние остановки) q
0
, попав в которое машина останавливается.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы алфавита A. Управляющее устройство работает согласно командам, которые имеют следующий вид
q
i
a
j
→a
p
Xq
k
Запись означает следующее: если управляющее устройство находится в состоянии q
i
, а в обозреваемой ячейке записана буква a
j
, то (1) в ячейку вместо a
j
записывается a
p
, (2) машина переходит к обозрению следующей правой ячейки от той, которая обозревалась только что, если Х= П, или к обозрению следующей левой ячейки, если Х= Л, или же продолжает обозревать ту же ячейку ленты, если Х= С, (3) управляющее устройство переходит в состояние q
k
.
Поскольку работа машины, по условию, полностью определяется ее состоянием q
, в данный момент и содержимым а
обозреваемой в этот момент ячейки, то для каждой возможной конфигурации q
i
a
j
имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Поэтому программа машины Тьюринга с внешним алфавитом A={a
0,
a
1, …,
a
n} и внутренним Q={q
1, q
2,…, q
m} содержит не более m (n+ 1) команд.
Словом
в алфавите А или в алфавите Q, или в алфавите A 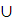 Q называется любая последовательность букв соответствующего алфавита. Под k-ой конфигурацией будем понимать изображение ленты машины с информацией, сложившейся на ней к началу k-того шага (или слово в алфавите А, записанное на ленту к началу k-того шага), с указанием того, какая ячейка обозревается в этот шаг и в каком состоянии находится машина. Имеют смысл лишь конечные конфигурации, т.е. такие, в которых все ячейки ленты, за исключением, быть может, конечного числа, пусты. Конфигурация называется заключительной
, если состояние, в котором при этом находится машина, заключительное. Q называется любая последовательность букв соответствующего алфавита. Под k-ой конфигурацией будем понимать изображение ленты машины с информацией, сложившейся на ней к началу k-того шага (или слово в алфавите А, записанное на ленту к началу k-того шага), с указанием того, какая ячейка обозревается в этот шаг и в каком состоянии находится машина. Имеют смысл лишь конечные конфигурации, т.е. такие, в которых все ячейки ленты, за исключением, быть может, конечного числа, пусты. Конфигурация называется заключительной
, если состояние, в котором при этом находится машина, заключительное.
Если выбрать какую-либо незаключительную конфигурацию машины Тьюринга в качестве исходной, то работа машины будет состоять в том, чтобы последовательно (шаг за шагом) преобразовывать исходную конфигурацию в соответствии с программой машины до тех пор, пока не будет достигнута заключительная конфигурация. После этого работа машины Тьюринга считается закончившейся, а результатом работы считается достигнутая заключительная конфигурация.
Будем говорить, что непустое слово б в алфавите А\ {а
0
} = {a
1
, …,
a
n
} воспринимается машиной в стандартном положении, если оно записано в последовательных ячейках ленты, все другие ячейки пусты, и машина обозревает крайнюю слева или крайнюю справа ячейку из тех, в которых записано слово б. Стандартное положение называется начальным (заключительным), если машина, воспринимающая слово в стандартном положении, находится в начальном состоянии q
1
(соответственно в состоянии остановки q
0
).
Если обработка слова б переводит машину Тьюринга в заключительное состояние, то говорят, что она применима к
б
, в противном случае – не применима к
б (машина работает бесконечно)
Рассмотрим пример:
Дана машина Тьюринга с внешним алфавитом А = {0, 1} (здесь 0 – символ пустой ячейки), алфавитом внутренних состояний Q = {q
0
, q
1
, q
2
} и со следующей функциональной схемой (программой):
q
1
0 → 1 Л q
2
;
q
1
1 → 0 Сq
2
;
q
2
0 → 0 П q
0
;
q
2
1 → 1 Сq
1
;
Данную программу можно записать с помощью таблицы
| 0 |
1 |
| q
1
|
1 Л q
2
|
0 С q
2
|
| q
2
|
0 П q
0
|
1 С q
1
|
Посмотрим, в какое слово переработает эта машина слово 110, исходя из начального положения:
q
1
На первом шаге действует команда: q
1
0 → 1 Л q
2
(управляющее устройство находится в состоянии q
1, а в обозреваемой ячейке записана буква 0, в ячейку вместо 0 записывается 1, головка сдвигается влево, управляющее устройство переходит в состояние q
2), в результате на машине создается следующая конфигурация:
q
2
На втором шаге действует команда: q
2
1 → 1Сq
1
и на машине создается конфигурация:
q
1
Третий шаг обусловлен командой: q
1
1 → 0 Сq
2
. В результате нее создается конфигурация:
q
2
Наконец, после выполнения команды q
2
0 → 0 П q
0
создается конфигурация
q
0
Эта конфигурация является заключительной, потому что машина оказалась в состоянии остановки q
0
.
Таким образом, исходное слово 110 переработано машиной в слово 101.
Полученную последовательность конфигураций можно записать более коротким способом (содержимое обозреваемой ячейки записано справа от состояния, в котором находится в данный момент машина):
11q
1
0 => 1q
2
11 => 1q
1
11 => 1q
2
01 => 10q
0
1
Машина Тьюринга – не что иное, как некоторое правило (алгоритм) для преобразования слов алфавита A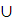 Q, т.е. конфигураций. Таким образом, для определения машины Тьюринга нужно задать ее внешний и внутренний алфавиты, программу и указать, какие из символов обозначают пустую ячейку и заключительное состояние. Q, т.е. конфигураций. Таким образом, для определения машины Тьюринга нужно задать ее внешний и внутренний алфавиты, программу и указать, какие из символов обозначают пустую ячейку и заключительное состояние.
4. Доказательство неразрешимости проблемы остановки
Проблема остановки машины Тьюринга
– это проблема построения такого алгоритма, который мог бы определить закончится или нет вычисление по некоторой задаче. Оказывается, что в общем случае такой алгоритм нельзя построить в принципе, то есть невозможно найти алгоритм, позволяющий по произвольной машине Тьюринга Т и произвольной ее начальной конфигурации q
i
a
j
определить придет ли машина Т в заключительное состояние q
0
, если начнет работу в этой конфигурации.
Если машина Т, запущенная в начальной конфигурации q
i
a
j
, останавливается (т.е. попадает в заключительное состояние) через конечное число шагов, то она называется самоприменимой, в противном случае – несамоприменимой.
Теорема.
Не существует машины Тьюринга М, решающей проблему самоприменимости, то есть проблема самоприменимости алгоритмически неразрешима.
Доказательство.
Предположим противное, то есть. пусть существует машина Тьюринга Т, решающая проблему самоприместимости в указанном выше смысле. Построим новую машину Т0
, добавив новое состояние q
0
* и объявив его заключительным, а также добавив новые команды для состояния q
0
, которое было заключительным в Т:
q
0
a
1
→ a
1
С q
0
(1)
q
0
a
2
→ a
2
С q
0
(2)
…
q
0
a
n
→a
n
С q
0
*
(n)
Рассмотрим теперь работу машины T0
.
Пусть M– произвольная машина. Если M– самоприменима, то начальная конфигурация q
1
a
i
перейдет с помощью команд машины T через конечное число шагов в конфигурацию q
0
a
1
, далее применяется команда (1), и машина T0
никогда не остановится. Если M– несамоприменима, то начальная конфигурация q
1
a
i
перейдет с помощью команд машины T через конечное число шагов в конфигурацию q
0
a
n
, далее применяется команда (n), и машина T0
остановится.
Таким образом, машина T0
применима к кодам несамоприменимых машин Т и неприменима к кодам самоприменимых машин Т.
Теперь применим машину T0
к начальной конфигурации q
1
a
i
. Сама машина T0
является либо самоприменимой, либо несамоприменимой. Если T0
самоприменима, то по доказанному она никогда не остановится, начав с q
1
a
i
, и потому она несамоприменима. Если T0
несамоприменима, то по доказанному, она останавливается через конечное число шагов, начав с q
1
a
j
, и потому она самоприменима. Получили противоречие, следовательно проблема самоприменимости алгоритмически неразрешима, что и требовалось доказать.
Проблема остановки алгоритмически неразрешима, т. к. если бы она была разрешимой, то мы получили бы разрешимость проблемы самоприменимости.
5. Неразрешимости логики первого порядка
В математической логике и теории алгоритмов под разрешимостью подразумевают свойство формальной теории обладать алгоритмом, определяющим по данной формуле, выводима она из множества аксиом данной теории или нет. Теория называется разрешимой, если такой алгоритм существует, и неразрешимой, в противном случае.
Вывод неразрешимости логики первого порядка из неразрешимости проблемы остановки
Вообще, говорят, что проблема распознавания какого-либо свойства разрешима, если существует допускающий механическое вычисление тест (вычислимая, или эффективная, процедура), который, будучи применен к произвольному объекту соответствующего типа, по прошествии некоторого времени правильно классифицирует этот объект с точки зрения наличия или отсутствия у него некоторого свойства. (Слова «по прошествии некоторого времени» означают здесь «после некоторого конечного числа шагов».) Позитивным тестом называется эффективная процедура, устанавливающая по прошествии некоторого времени все случаи наличия соответствующего свойства и только их. Негативный тест – это эффективная процедура, обнаруживающая все случаи отсутствия свойства и только их. Проблема распознавания произвольного свойства разрешима тогда и только тогда, когда для него существует и позитивный, и негативный тесты; дело в том, что всякий объект может или обладать рассматриваемым свойством, или нет, и потому, обладая обоими тестами, можно применить их оба к интересующему объекту, выполняя поочередно шаги одного и другого, и после некоторого их количества обнаружить, обладает он этим свойством или нет. (Верно и обратное: всякий тест, устанавливающий через некоторое конечное число шагов, обладает данный объект рассматриваемым свойством или нет, реализует и позитивный, и негативный тесты для этого свойства) Нас будут интересовать сейчас свойства общезначимости и выполнимости, а в роли объектов «соответствующего типа» выступают формулы языка логики первого порядка.
Докажем, что для этих тестов не существует дополнительных – позитивного для выполнимости и негативного для общезначимости – и потому в логике первого порядка проблемы распознавания как общезначимости, так и выполнимости неразрешимы.
Докажем неразрешимость логики первого порядка от противного: покажем, что если бы соответствующий тест существовал, то проблема остановки оказалась бы разрешимой. Мы убедились, что проблема остановки неразрешима.
Наше доказательство от противного будет строиться так: мы покажем, как, располагая программой машины Тьюринга, а также натуральным числом n
, можно эффективно построить такие конечное множество предложений Д и еще одно предложение Н, что Д ├ Н тогда и только тогда, когда рассматриваемая машина, будучи запущенной в состоянии n
(т.е. когда она начинает работу в состоянии q
1
, считывая при этом самую левую единицу в сплошном массиве из n
единиц на ленте с пустыми символами в остальных клетках), в конце концов останавливается. Таким образом, мы определяем некоторую интерпретацию машины Тьюринга I. Формула Н в интерпретации I говорит, что машина в конце концов остановится, а формула из множества Д описывают работу машины. Введем функцию следования ' (где i' = i + 1 для всякого i). Таким образом, если бы мы могли решить проблему распознавания общезначимости предложений, мы смогли бы эффективно решать, остановится в конце концов или нет данная машина Тьюринга, поскольку логическое следование Д ├ Н имеет место тогда и только тогда, когда общезначима импликация F1
 F2 F2
 … … Fk
→H, где Fi Fk
→H, где Fi
 Д (i = 1,2,… k). Д (i = 1,2,… k).
Будем считать, что клетки ленты машины Тьюринга занумерованы так:
Будем также предполагать, что время разбито на бесконечную последовательность моментов t, в каждый из которых машина выполняет точно одну свою операцию, и что машина начинает работу в момент времени 0, считывая при этом содержимое клетки 0. Моменты времени предполагаются неограниченно продолжаемыми как в будущее, так и в прошлое, равно как и лента бесконечно простирается и вправо, и влево. Мы считаем, что машина «включается» в момент 0 и «выключается» в первый момент (если таковой наступит), который следует за моментом ее остановки; мы считаем, далее, что во все отрицательные моменты времени и во все моменты, следующие за моментом остановки машины, она не находится ни в каком состоянии, не считывает никакую из имеющихся клеток и никакой символ (даже пустой) не встречается нигде на ее ленте.
Каждому состоянию q
i
, в котором может пребывать машина, ставится в соответствие некоторый двуместный предикатный символ Qi
, подобным же образом каждому символу a
j
, который машина может считывать либо записывать, ставится в соответствие двуместный предикатный символ Aj
. Помимо символов Qi
и Aj
в формулах из множества Д 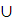 {Н} могут встречаться только следующие символы: имя 0, одноместный функциональный символ ' и двуместный предикатный символ <. {Н} могут встречаться только следующие символы: имя 0, одноместный функциональный символ ' и двуместный предикатный символ <.
В предполагаемой интерпретации I предложений из множества Д 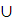 {Н} предметной областью являются целые числа. Имени 0 интерпретация I приписывает значение нуль, а функциональному символу ' – функцию следования. Символы Qi
, Aj
и < интерпретируются следующим образом: {Н} предметной областью являются целые числа. Имени 0 интерпретация I приписывает значение нуль, а функциональному символу ' – функцию следования. Символы Qi
, Aj
и < интерпретируются следующим образом:
I объявляет Qi
истинным на паре t, x в точности тогда, когда машина в момент времени t находится в состоянии q
i
, считывая при этом клетку с номером х
.
I объявляет a
j
истинным на паре t, x в точности тогда, когда вмомент t в клетке с номером х
находится символ a
j
;
I объявляет < истинным на паре х, у в точности тогда, когда х меньше чем у.
Выясним теперь, какие функции содержатся в множестве Д. (Будем использовать переменную t в тех случаях, когда имеется в виду время, и переменные х и у, когда речь идет о клетках на ленте.) Пусть a
i
, …, a
n
– список символов, считываемых и записываемых машиной. Для каждой строки программы вида q
i
a
j
→a
p
Cq
k
мы включаем в множество Д формулу
(1) "x
"y
"t
((t
Qi
x
 t
Aj
x
) → (t
' Qk
x t
Aj
x
) → (t
' Qk
x
 t
Ap
x t
Ap
x
 (y
≠ x
→ (t
A0
y
→ t
'A0
y (y
≠ x
→ (t
A0
y
→ t
'A0
y
 … …  t
An
y
→ t
'An
y
)
))) t
An
y
→ t
'An
y
)
)))
(«Если в момент времени t машина находится в состоянии q
i
, считывая при этом символ a
j
в клетке х
, то в момент t
+ 1 машина перейдет в состояние q
k
, считывая при этом клетку х
, в которой появится символ Ap
, а во всех клетках, отличных от х
, в момент t
+ 1 останутся те же символы, что в момент t
для всех t
и х.
»)
Также в множество Д для каждой строки программы вида q
i
a
j
→a
j
П q
k
мы включаем формулу
(2) "x
"y
"t
((t
Qi
x
 t
Aj
x
) → (t
' Qk
x
' t
Aj
x
) → (t
' Qk
x
' (t
A0
y
→ t
'A0
y) (t
A0
y
→ t
'A0
y)
 … …  (t
An
y
→ t
'An
y
))) (t
An
y
→ t
'An
y
)))
(«Если в момент времени t машина находится в состоянии q
i
, считывая при этом символ a
j
в клетке х
, то в момент t
+ 1 машина перейдет в состояние q
k
, считывая при этом клетку х
+ 1, и во всех клетках в момент t
+ 1 останутся те же символы, что в момент t
для всех t
и х.
»)
Аналогично для строк вида q
i
a
j
→a
j
Л q
k
включаем в Д
(3) "x
"y
"t
((t
Qi
x
' t
Aj
x
') → (t
' Qk
x t
Aj
x
') → (t
' Qk
x
 (t
A0
y
→ t
'A0
y) (t
A0
y
→ t
'A0
y)
 … …  (t
An
y
→ t
'An
y
))) (t
An
y
→ t
'An
y
)))
(«Если в момент времени t машина находится в состоянии q
i
, считывая при этом символ a
j
в клетке х
+ 1, то в момент t
+ 1 машина перейдет в состояние q
k
, считывая при этом клетку х
, и во всех клетках в момент t
+ 1 останутся те же символы, что в момент t
для всех t
и х.
»)
Одно из предложений множества Д утверждает, что в начальный момент машина находится в состоянии q
1
, считывая при этом самую левую единицу в сплошном массиве единиц на ленте с пустыми символами в остальных клетках:
(4) 0 Qi
0  0 A1
0 0 A1
0  0 A1
0' 0 A1
0'  … …  0 A1
0(n-1) 0 A1
0(n-1)
 "y
((y
≠ 0 "y
((y
≠ 0  y
≠ 0' y
≠ 0'  … …  y
≠ 0(
n
-1))
→ 0 A0
y
) y
≠ 0(
n
-1))
→ 0 A0
y
)
Здесь 0(
n
-1)
обозначает результат применения n символов следования к символу 0.
Еще одна из формула множества Д утверждает, что всякое целое число является следующим точно за одним целым:
(5) "z
$x
z
= x
'  "z
"x
"y
(z
= x
' "z
"x
"y
(z
= x
'  z
= y
' → x
= y
) z
= y
' → x
= y
)
Введем в Д еще одну формулу
(6) "x
"y
"z
(x
<y
 y
<
z
→ x
<
z
) y
<
z
→ x
<
z
)  "x
"y
(x
' =
y
→ x
<
y
) "x
"y
(x
' =
y
→ x
<
y
)
 "x
"y
(x
< y
→ x
≠ y
), "x
"y
(x
< y
→ x
≠ y
),
из которого следует, что если p и q – различные натуральные числа, то "x
x
(
p
)
≠ x
(
q
)
.
Таким образом, Д состоит из формул (1), (2), (3), соответствующих всем командам машины, и трема дополнительными (4), (5), (6). Что касается предложения Н, то заметим, что всякая машина останавливается в момент времени t, если она в это время находится в состоянии q
i
, считывая при этом символ a
j
, причем в машинной таблице нет команды, соответствующей комбинации q
i
a
j
. Таким образом, за предложение Н мы принимаем дизъюнкцию всех предложений вида
$t
$x
(t
Qi
x
 t
Ai
x
), t
Ai
x
),
для которых в машинной таблице нет команд, соответствующих комбинациям q
i
a
j
. Если же для всякой такой комбинации в таблице имеются команды, то машина никогда не остановится, и за Н в этом случае мы принимаем какую-либо формулу, ложную в интерпретации I, например 0 ≠ 0.
Мы показали, как по данной машине и входному значению n
построить такие конечное множество предложений Д и отдельное предложение Н, что соотношение Д ├ Н имеет место тогда и только тогда, когда машина, получив n
на входе, в конце концов, останавливается.
Рассмотрим факты, касающиеся отношения ├ в логике первого порядка. Все предложения из множества Д истинны в интерпретации I. Поэтому если Д ├ Н, то и Н истинно в I. Но Н истинно в I тогда и только тогда, когда машина, получив на входе n
, в конце концов останавливается.
Введем теперь один специальный тип формул, называемых нами описаниями времени s. Так называется всякая формула, определяющая очевидным способом, в каком состоянии находится машина в момент s, какая клетка ею в это время считывается, а также в каких клетках ленты какие символы записаны, причем все это делается на языке множества формул Д  {Н}. Точнее говоря, всякое описание времени s есть формула вида {Н}. Точнее говоря, всякое описание времени s есть формула вида
(7) 0(s)
Qi
0(p)
 0(s) 0(s)
  … …  0(s)
Aj
0(p) 0(s)
Aj
0(p)
 … …  0(s) 0(s)
  "y
((y "y
((y
   … …  y y
 0(p) 0(p)
 … …  y y
  ) → 0(s)
A0
y) ) → 0(s)
A0
y)
Мы требуем при этом, чтобы последовательность целых чисел p1
,…, р,…, pv
была возрастающей; р может совпадать с р1
или с рv
Заметим, что формула (4) является описанием времени 0.
Предположим теперь, что машина, получив на входе число n
, в конце концов останавливается. Тогда для некоторых s, i, p и j машина в момент s окажется в состоянии qi
, считывая при этом клетку с номером р, содержащую символ aj, причем в программе машинной нет команды для комбинации q
i
a
j
.
Предположим, далее, что из множества формул Д следует некоторое описание G времени s. Поскольку I– модель для Д, формула G должно быть истинным в I. Поэтому G должно содержать в качестве конъюнктивных членов формулы 0(
s
)
Qi0(
p
)
и 0(
s
)
Aj0(
p
)
а потому из G должна следовать формула
$t
$x
(t
Qix
 t
Ai x
), t
Ai x
),
входящее одним из дизъюнктивных членов в H. Поэтому Н будет следовать из Д.
Остается лишь показать, что для всякого неотрицательного s, если только машина не останавливается до момента
s
, из Д следует некоторое описание времени
s
. Докажем это индукцией по s.
Основание индукции. Пусть s = 0. Множество Д содержит, а потому и влечет за собой предложение (4), являющееся описанием времени 0.
Шаг индукции. Предположим, что выделенное курсивом предложение верно (для s). Предположим, далее, что наша машина не остановилась до момента s + 1. Это значит, что она не остановилась ни до момента s, ни в самый момент s. Тогда из Д следует некоторое описание (8) времени s. Нужно доказать, что из Д следует и некоторое описание времени s+1.
Поскольку I– модель для Д, формула (8) истинна в I. Поэтому в момент s машина находится в состоянии qi, считывая при этом некоторую клетку (с номером р), в которой записан символ aj. Поскольку машина в момент s не остановилась, в ее программе должна присутствовать команда одного из видов
(a)q
i
a
j
→ a
k
С q
m
(б)q
i
a
j
→ aj
П q
m
(в)q
i
a
j
→ aj
Л q
m
Если имеется команда типа (а), то одна из формул множества Д есть
"x
"y
"t
((t
Qi x
 t
Aj x
) → (t
' Qk x t
Aj x
) → (t
' Qk x
 t
Ap x t
Ap x
 (y
≠ x
→ (t
A0y
→ t
'A0y (y
≠ x
→ (t
A0y
→ t
'A0y
 … …  t
Any
→ t
'Any
)
))) t
Any
→ t
'Any
)
)))
Она вместе с (5), (6) и (8) влечет за собой формулу
0 (s+1) Qi0 (p)  0 (s+1) Aj10 (p1) 0 (s+1) Aj10 (p1)  … …  0 (s+1) Aj0 (p) 0 (s+1) Aj0 (p)  … …  0 (s+1) Ajv0 (pv) 0 (s+1) Ajv0 (pv)  "y
((y
≠ 0 (p1) "y
((y
≠ 0 (p1)  … …  y
≠ 0 (p) y
≠ 0 (p)  … …  y
≠ 0 (pv)) → 0 (s+1) A0y
), y
≠ 0 (pv)) → 0 (s+1) A0y
),
являющуюсяописаниемвремени s + 1.
Еcли имеется команда типа (б), то одна из формул множества Д есть
"x
"y
"t
((t
Qi
x
 t
Aj
x
) → (t
' Qk
x
' t
Aj
x
) → (t
' Qk
x
' (t
A0
y
→ t
'A0
y) (t
A0
y
→ t
'A0
y)
 … …  (t
An
y
→ t
'An
y
))) (t
An
y
→ t
'An
y
)))
Из этого предложения, объединенного с (5), (6) и (8), следует, что для некоторого символа  , ,
0(s+1)
Qi
0(p+1)
 0(s+1) 0(s+1)
  … …  0(s+1)
Aj
0(p+1) 0(s+1)
Aj
0(p+1)
 … …  0(s+1) 0(s+1)
  "y
((y
≠ "y
((y
≠   … …  y
≠ 0(
p
+1) y
≠ 0(
p
+1)
 … …  y
≠ y
≠  ) → 0(
s
+1)
A0
y
), ) → 0(
s
+1)
A0
y
),
а это предложение является описанием времени s + 1.
Если имеется стрелка типа (в), то одна из формул множества Д есть
"x
"y
"t
((t
Qi
x
' t
Aj
x
') → (t
' Qk
x t
Aj
x
') → (t
' Qk
x
 (t
A0
y
→ t
'A0
y) (t
A0
y
→ t
'A0
y)
 … …  (t
An
y
→ t
'An
y
))) (t
An
y
→ t
'An
y
)))
Тогда существует такой символ a
q, что из последней формулы, объединенной с (5), (6), (8), следует
0(s+1)
Qi
0(p-1)
 0(s+1) 0(s+1)
  … …  0(s+1)
Aj
0(p-1) 0(s+1)
Aj
0(p-1)
 … …  0(s+1) 0(s+1)
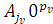  "y "y
((y
  y y
 0(
p
-1) 0(
p
-1)
 … …  y y
 )
→ 0(
s
+1)
A0
y
) )
→ 0(
s
+1)
A0
y
)
а это предложение является описанием времени s + 1.
Во всех трех случаях множество Д имеет следствием некоторое описание времени s + 1, и тем самым неразрешимость логики первого порядка доказана.
Для доказательства неразрешимости логики первого порядка достаточно продемонстрировать, как по данной машине Т с входным значением n
(то есть когда машина находится на самой левой единице в сплошной последовательности из n
единиц при пустых символах в остальных клетках ленты) построить такие предложение Iи конечное множество предложений Г, что машина Т при входном значении  останавливается тогда и только тогда, когда Г ├ I. останавливается тогда и только тогда, когда Г ├ I.
Не существует эффективной процедуры, позволяющей решать, останавливается ли произвольная машина Тьюринга Т при произвольном входном значении n
и по данной машине Тьюринга Т можно построить примитивно рекурсивную функцию g
, обладающую следующим свойством: какое бы n
мы не взяли, g
(n
, t
) = 0 в точности тогда, когда t
– номер шага, более позднего, чем тот, на котором машина T останавливается, если ее запустить при входном значении n
. (по определению функции g
, если шаг t
не таков, то g
(x
, t
) = <a
, b
, c
> =  для некоторых a
, b
, c
и потому g
(x
, t
) > 0. Если же t
– такой шаг, то g
(x
, t
) = 0. для некоторых a
, b
, c
и потому g
(x
, t
) > 0. Если же t
– такой шаг, то g
(x
, t
) = 0.
Таким образом, если дана машина Т, то можно эффективно построить некоторую конечную последовательность q0
, q1
, …, qr
примитивно рекурсивных функций, удовлетворяющую двум условиям: 1) каждая функция g
i
либо является базисной функцией, либо получается из некоторых предыдущих функций с помощью композиции или примитивной рекурсии и 2) для всякого n
машина T, запущенная на входном значении n
, в конце концов останавливается тогда и только тогда, когда g
r
(n
,
t
) = 0 для некоторого t
.
Построим теперь по данной T последовательность примитивно рекурсивных функций, удовлетворяющую условиям 1) и 2). Каждой функции g
i
поставим в соответствие свой функциональный символ g
i
с тем же числом аргументов, что иg
i
. Пусть g
0
= '. Используя эти символы, выпишем для каждого g
i
одну или две очевидные формулы, определяющие функцию g
i
Например,
если g
i
= z, то "x
g
i
(x
) = 0
еслиg
i
= s
, то "x
g
i
(x
) = x
'
если g
i
=  , то "x
1
… "x
m
… "x
n
g
i
(x
1
, …,x
m
, …,x
n
) = x
m , то "x
1
… "x
m
… "x
n
g
i
(x
1
, …,x
m
, …,x
n
) = x
m
Если g
i
получается из предшествующих ей функций g
j
и g
k
c помощью примитивной рекурсии, то "x
g
i
(x
, 0) =g
j
(x
) и "x
"y
g
i
(x
, y
') =g
k
(x
, y
,
g
i
(x
, y
))
Если же g
i
получается из предшествующих ей функций g
о
и  путем композиции, то "x
g
i
(x
) =g
j путем композиции, то "x
g
i
(x
) =g
j
 (для краткости заменили здесь x
1
, x
2
, …, x
n
на x
, a"x
1
, "x
2
, …, "x
n
на "x
) (для краткости заменили здесь x
1
, x
2
, …, x
n
на x
, a"x
1
, "x
2
, …, "x
n
на "x
)
Запишем также формулы "x
x
' ≠ 0 и "x
"y
(x
' = y
' → x
= y
). Обозначим теперь через Г множество всех этих формул, а через I – формулу 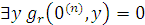 . .
Утверждение. Машина T при входном значении  останавливается тогда и только тогда, когда Г ├ I. останавливается тогда и только тогда, когда Г ├ I.
«Тогда». Пусть Г ├ I. Обозначим через  модель, областью которой служит множество натуральных чисел и которая интерпретирует символ 0 как 0, а функциональные символы gi
– как модель, областью которой служит множество натуральных чисел и которая интерпретирует символ 0 как 0, а функциональные символы gi
– как  . Все предложения из Г истинны в . Все предложения из Г истинны в  . Поскольку Г ├ I, предложение Iистинно также. Следовательно, для некоторого . Поскольку Г ├ I, предложение Iистинно также. Следовательно, для некоторого  справедливо справедливо  . Согласно 2), T останавливается на . Согласно 2), T останавливается на  . .
«Только тогда». Предположим, что Т останавливается при входном значении  . Для доказательства соотношения Г ├ I предположим, что . Для доказательства соотношения Г ├ I предположим, что  – произвольная модель, в которой все предложения из Г истинны, и покажем, что из этого предположения следует истинность – произвольная модель, в которой все предложения из Г истинны, и покажем, что из этого предположения следует истинность  в в  . Пусть теперь . Пусть теперь 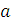 – интерпретация символа 0 в модели – интерпретация символа 0 в модели  , a , a  – при всяком – при всяком 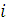 – интерпретация в – интерпретация в  символа gi
. Пусть, далее, символа gi
. Пусть, далее,  (так что (так что  – интерпретация в – интерпретация в  символа символа  ), и пусть ), и пусть  . Так как формулы . Так как формулы  и и  истинны в истинны в  , функция , функция  , для которой , для которой  и и  , является изоморфизмом множества {0, 1, 2,…} натуральных чисел на множество N. Таким образом, можно считать, что N и является в действительности множеством натуральных чисел, , является изоморфизмом множества {0, 1, 2,…} натуральных чисел на множество N. Таким образом, можно считать, что N и является в действительности множеством натуральных чисел,  , ограничение функции , ограничение функции  на множество N есть на множество N есть  , а потому всякий нумерал е обозначает число , а потому всякий нумерал е обозначает число  в в  . .
Индукцией по  легко доказывается, что для всех легко доказывается, что для всех  р в N справедливо р в N справедливо 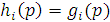 (а потому (а потому  N). Рассмотрим в деталях наиболее трудный случай, когда функция N). Рассмотрим в деталях наиболее трудный случай, когда функция  получается примитивной рекурсией из функций получается примитивной рекурсией из функций  и и  причем причем . Итак, пусть для всех . Итак, пусть для всех  из N выполняются равенства из N выполняются равенства  .Нам нужно доказать, что .Нам нужно доказать, что 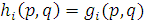 для всех для всех  и и 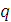 . Но так как формулы . Но так как формулы 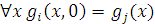 и и  содержатся в Г, справедливы равенства содержатся в Г, справедливы равенства  и и 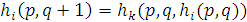 . Но тогда . Но тогда  и если и если  , то, полагая , то, полагая  , получим , получим  . Таким образом, индукцией по . Таким образом, индукцией по 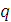 заключаем, что заключаем, что 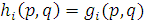 для всех для всех  и и 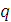 . .
Поскольку  при входном значении при входном значении  останавливается, можно утверждать, что для некоторого останавливается, можно утверждать, что для некоторого  справедливо справедливо  , откуда , откуда  , а потому , а потому  истинно в истинно в  , а значит, и I = , а значит, и I = 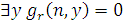 истинно в истинно в  , и доказательство заканчивается. , и доказательство заканчивается.
Логика первого порядка обладает рядом полезных свойств, которые делают ее очень привлекательной в качестве основного инструмента формализации математики. Главными из них являются полнота (это означает, что для любой формулы выводима либо она сама, либо ее отрицание) и непротиворечивость (ни одна формула не может быть выведена одновременно со своим отрицанием).
Логика первого порядка обладает свойством компактности: если некоторое множество формул невыполнимо, то невыполнимо также некоторое его конечное подмножество.
Являясь формализованным аналогом обычной логики, логика первого порядка дает возможность строго рассуждать об истинности и ложности утверждений и об их взаимосвязи, в частности, о логическом следовании одного утверждения из другого, или, например, об их эквивалентности.
В ходе исследования были рассмотрены основные понятия логики первого порядка и изучены доказательства неразрешимости логики первого порядка. Для этого было разобрано понятие машины Тьюринга, доказана неразрешимость проблемы ее остановки. На основе полученного выведена неразрешимость логики первого порядка. Так же разобрано доказательство неразрешимости логики первого порядка методом Геделя.
1.Булос Дж., Джеффри Р. Вычислимость и логика – Москва «Мир»: 1994.-394 с.
2.Зюзюков В.М., Шелупанов А.А. Математическая логика и теория алгоритмов – М: 2007.-176 с.
3.Игошин В.И. Математическая логика и теория алгоритмов – М: 2008. -435 с.
4.Мендельсон Э. Введение в математическую логику – М: 1971.-320 с.
5.Молчанов В.А. Математическая логика – Оренбург: ИПК ГОУ ОГУ, 2009. -88 с.
6.http://ru.wikipedia.org/wiki/Логика_первого_порядка
7.http://ru.wikipedia.org/wiki/Машина_Тьюринга
8.http://ru.wikipedia.org/wiki/Формальное_исчисление
|