Автор: Фильчев Э.Г.
Решение кубического уравнения в системе mn параметров
Решение кубического уравнения на основе современных методов не представляется тривиальным. В любом справочнике по математике предлагаются следующие методы
- разложение левой части на линейные множители ( если возможно )
- с помощью формулы Кардана
- применение специальных таблиц
(см. например, И.Н.Бронштейн. К.А.Семендяев. Справочник по математике …М. Наука 1980. стр.219).
В данной статье рассматривается метод решения любых кубических уравнений включая неприводимый случай формулы Кардана!
Задача
"Задано кубическое уравнение вида ax3 + bx2+ cx + в = 0.
Используя формулы системы mn параметров предложить метод определения нулей исходного уравнения ". Пусть а = 1.
Решение
На сайте fgg-fil1.narod.ru/fmat16.doc приведена, полученная автором, формула mn
преобразования степенной функции. Для кубического уравнения эта формула имеет вид
(2
mn
)2
+ ( 3
x
+
b
)(2
mn
) + 3
x
2
+ 2
bx
+с = 0 ( 1 )
где
x- любой из нулей ( корней) исходного уравнения
2mn - разность любой пары из трех нулей исходного уравнения
Решив уравнение (1) относительно х и подставив это значение в исходное уравнение, в результате, после простых, но громоздких преобразований, получим
(2mn)6
+2( 3c – b2
)(2mn)4
+(3c – b2
)2
(2mn)2
+ [ 4( 3c – b2
)3
+ ( 2b3
– 9bc + 27d )2
]/27 = 0 ( 2 )
Это уравнение устанавливает связь коэффициентов исходного уравнения с параметром (2mn) и является кубическим относительно (2mn)2. На основании формул Виета и уравнения (2) можно сделать следующее утверждение
Утверждение1 "Для любого кубического уравнения вида x3 + bx2+ cx + в = 0 справедливы уравнения
3x2 + 2bx + c
= - (2mn)1( 2mn)2
2(3c-b2) = - [(2mn)12+( 2mn)22+( 2mn)32 ]
[4(3c-b2)3+(2b3 - 9bc+27d)2]/27 = - (2mn)12( 2mn)22( 2mn)32
где (2mn)j
- разность любой пары корней исходного уравнения.
x - один ( любой ) из корней исходного уравнения. "
1. Для любого кубического уравнения вида x3 + bx2+ cx + в = 0 определяем значение
D1
= -
 = - (2mn)1
2
∙( 2mn)2
2
∙ ( 2mn)3
2 = - (2mn)1
2
∙( 2mn)2
2
∙ ( 2mn)3
2
2. Определяем значение
D
2
= - 2( 3c –
b
2
) = - [(2mn)12 + ( 2mn)22 + ( 2mn)32]
Из этих уравнений следует, что
- если выражение - 2(3c - ) - целое число, то оно разложимо на сумму трех квадратов
-
и если при этом выполняется равенство
D
1
= - (2mn)12( 2mn)22( 2mn)32
, то в результате получим решение для (2mn)1,( 2mn)2,( 2mn)3.
3
. Определяем значение корней исходного уравнения
3
x
2
+ 2
bx
+
c
= - (2
mn
)1( 2
mn
)2
3x2 + 2bx + c
= (2mn)1( 2mn)2
3x2 + 2bx + c
= - (2mn)1( 2mn)3
3x2 + 2bx + c
= (2mn)1( 2mn)3
3x2 + 2bx + c
= - (2mn)2( 2mn)3
3
x
2
+ 2
bx
+
c
= (2
mn
)2( 2
mn
)3
Задача решена !
Пример 1
Решить уравнение с помощью формул системы mn параметров
x3 -9x2+ 23x - 15 = 0
где
a =1, b = - 9, c = 23, в = -15
Решение
1. Определяем значение
D1
= = - 
-→ D1
= - [4(69-81)3+( - 1458 + 1863 - 405)2]/27= - [4(69-81)3+0]/27= 256 = 162
Обратим внимание, что в этом примере (2b3-9bc+27d) = 0
2.
Определяем значение
D2
= - 2(3c - )
-→ D2
= - 2( 3∙23 - 81 ) = 24 = 4 + 16 + 4
Это единственное разложение числа 24 на три квадрата. Следовательно
имеем (2mn)1
= 2, (2mn)2
= 4, (2mn)3
= 2.
3
. Определяем значение нулей ( корней ) исходного уравнения
3.1
3x2 + 2bx + c
= - (2mn)1( 2mn)2
-→ 3x2 - 18x + 23 = - -> 3x2 - 18x + 31 = 0. Нет действительных решений.
3.2
3
x
2
+ 2
bx
+
c
= (2
mn
)1( 2
mn
)2
-→ 3x2 - 18x + 23 = -> 3x2 - 18x + 15 = 0 -→ x2 - 6x + 5 = 0
-→ X
1
= 3 + 2 = 5
, X
2
= 3 - 2 = 1
Здесь
X
1
= 5
- одно из решений исходного уравнения.
Здесь
X
2
= 1 второе решение исходного уравнения.
3.3 3x2 + 2bx + c
= - (2mn)1( 2mn)3
-→ 3x2 - 18x + 23 = - -> 3x2 - 18x + 27 = 0 -→ x2 - 6x + 9 = 0
-→ X2
= 3
Здесь
X
= 3
- последнее из решений исходного уравнения.
3.4 3
x
2
+ 2
bx
+
c
= (2
mn
)1( 2
mn
)3
-→ 3x2 - 18x + 23 = 2∙2-→ 3x2 - 18x + 19 = 0. Нет решений исходного уравнения.
Задача решена!
Пример 2
Решить уравнение с помощью формул системы mn параметров
x3 -20x2+ 113x - 154 = 0
где
a =1, b = - 20, c =113, в = -154
Решение
1. Определяем значение
D1
= - 
-→D1
= - [4(339-400)3+( - 16000 + 20340 - 4158)2]/27= - [- 907924+33124]/27=32400
2.
Определяем значение
D2
= - 2(3c - )
-→ D2
= - 2( - 400 ) = 122 = 32
+ 72
+ 82
= 42
+ 52
+ 92
Здесь имеет место два представления числа 122 в виде суммы трех квадратов.
Поэтому, проверяем на соответствие с числом D1
= 32400.
2.1
32
∙ 72
∙ 82
= 28224 ≠ 32400
2.2
42
∙ 52
∙ 92
= 32400 . Этот вариант подходит!
-→ (2mn)11
= 4, (2mn)12
= - 4,
(2mn)21
= 5, (2mn)22
= - 5,
(2mn)31
= 9, (2mn)32
= - 9.
3
. Определяем значение нулей ( корней ) исходного уравнения
3.1
3x2 + 2bx + c
= - (2mn)1( 2mn)2
-→ 3x2 - 40x + 113 = - 4∙5-> 3x2 - 40x + 133 = 0.
-→ X
1
= 7,
X2
= 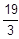
4.
Таким образом, определен один из корней исходного кубического уравнения X1
= 7,
и кроме того, известны значения (2mn)11
÷ (2mn)32
. Этих данных достаточно для определения двух остальных корней.
4.1
Пусть (2mn)11
= 4 = (X
1
-
X
2
) -→ X
2
= X
1
– 4 = 7 – 4 = 3. Нет решения(это не корень).
4.2
Пусть (2mn)12
= - 4 = (X
1
-
X
2
) -→ X
2
= X
1
+ 4 = 7 + 4 = 11
. Это второй корень.
4.3
Пусть (2mn)21
= 5 = (X
2
-
X
3
) -→ X
3
= X
2
- 5 = 7 - 5 = 2
. Это третий корень.
Решением исходного уравнения будет X1
= 7
, X2
= 2,
X3
= 11.
Расчет закончен !
Пример 3
Решить уравнение с помощью формул системы mn параметров
x3 -10x2 - 49x + 130 = 0
где
a =1, b = - 10, c = - 49, в = 130
Решение
1. Определяем значение
D1
= - 
-→D1
= - [4( -147 - 100)3+( 2000 + 4410 - 3510)2]/27= - [- 60276892+8410000]/27= 1920996
2.
Определяем значение
D2
= - 2( 3c - )
-→ D2
= - 2( - 147 - 100 ) = 494 = 12
+ 32
+ 222
= 22
+ 72
+ 212
= 72
+ 112
+ 182
Из этих трех вариантов представления числа 494 в виде суммы трех квадратов подходит последний вариант , т.к. 72
∙ 112
 182
= 1920996 182
= 1920996
-→ (2mn)11
= 7, (2mn)12
= - 7,
(2mn)21
= 11, (2mn)22
= - 11,
(2mn)31
= 18, (2mn)32
= - 18.
3
. Определяем значение нулей ( корней ) исходного уравнения
3.1
3x2 + 2bx + c
= - (2mn)11( 2mn)21
-→ 3x2 - 20x - 49 = 7∙11-> 3x2 - 20x - 126 = 0. Эти значения X не подходят!
3.2
3x2 + 2bx + c
= (2mn)11( 2mn)22
-→ 3x2 - 20x - 49 =- 77 -→ 3x2 - 20x + 28 = 0.
-→ X1
=  ,
X2
= 2 – это один из корней исходного уравнения! ,
X2
= 2 – это один из корней исходного уравнения!
4.
Таким образом, определен один из корней исходного кубического уравнения X1
= 2,
и кроме того, известны значения (2mn)11
÷ (2mn)32
. Этих данных достаточно для определения двух остальных корней.
4.1
Пусть (2mn)11
= 7 = (X
1
-
X
2
) -→ X
2
= X
1
– 7 = 2 – 7 = - 5
. Это второй корень!
4.2
Пусть (2mn)12
= - 7 = (X
1
-
X
2
) -→ X
2
= X
1
+7 = 2 + 7 = 9. Это не корень.
4.3
Пусть (2mn)21
= 11 = (X
1
-
X
3
) -→ X
3
= X
1
- 11= 2 - 11 = - 9. Это не корень.
4.4
Пусть (2mn)21
= -11 = (X
1
-
X
3
) -→ X
3
= X
1
+ 11= 2 + 11 = 13. Это третий корень!
Решением исходного уравнения будет X1
= 2
, X2
= - 5,
X3
= 13.
Расчет закончен !
Пример 4
Решить уравнение с помощью формул системы mn параметров
x3 -6.85x2 + 13.425x – 8.1 = 0
где
a =1, b = - 6.85, c = 13.425, в = - 8.1
В этом уравнении имеют место нецелые значения коэффициентов. Это указывает на то, что и корни также могут иметь нецелые значения.
Решение
1. Определяем значение
D1
= - 
-→D1
= - [4( 40.275 – 46.9225)3+(- 642.83825 + 827.65125 – 218.7)2]/27
-→D1
= - [- 1174.9923236875+1148.328769]/27= 0.987539062500
2.
Определяем значение
D2
= - 2( 3c - )
-→ D2
= - 2(40.275 – 46.9225 ) = 13.2950
В этом случае имеют место дробные значения для D1
и D2
. Предлагаемый метод решения куб.уравнения оперирует только с целыми числами, поэтому необходимо умножить на 10k
.
При этом значение степени k должно определяться
- для D2
числом знаков в мантиссе ( для данного примера k2
= 4 )
- для D1
=3∙ (число знаков в мантиссе для D2
). -→ k1
= 3∙ k2
( для данного примера k1
= 12 ).
Для дальнейшего рассмотрения используем два числа
- D11
= 987539062500
- D21
= 132950.
3.
Далее задача заключается в том, чтобы определить три значения таких целых чисел ( А,Б,Д), при которых выполняются равенства D
21
= А2
+ Б2
+ Д2
и D
11
= А2
∙ Б2
∙ Д2
.
Для нахождения значений чисел А,Б,Д можно использовать две методики
- найти все варианты представления числа D21
в виде суммы трех квадратов. При этом один из этих вариантов будет соответствовать условию D
21
= А2
+ Б2
+ Д2
и D
11
= А2
∙ Б2
∙ Д2
.
- найти все варианты представления числа D11
в виде произведения трех квадратов. При этом один из этих вариантов будет соответствовать условию D
21
= А2
+ Б2
+ Д2
и D
11
= А2
∙ Б2
∙ Д2
.
Вариант D
11
= А2
∙ Б2
∙ Д2
следует считать более удобным.
Для рассматриваемого примера
D11
= 987539062500 = 2502
∙ 2652
∙ 152
D21
= 132950 = 2502
+ 2652
+ 152
.
4.
В расчетах п.2 была произведена операция перехода к целым числам путем умножения соответствующих чисел на множители k1
и k2
. Совершая обратную операцию, получим
(2mn)11
= 2.5, (2mn)12
= - 2.5,
(2mn)21
= 2.65, (2mn)22
= - 2.65,
(2mn)31
= 0.15, (2mn)32
= - 0.15.
5
. Определяем значение нулей ( корней ) исходного уравнения
5.1
3
x
2
+ 2
bx
+
c
= - (2
mn
)11( 2
mn
)21
-→ 3x2 - 2∙(6.85)∙ x + 13.425 = (2.5)∙(2.65)-> 3x2 – 13.7x + 6.8 = 0.
-→ X1
= 4 – это один из корней исходного уравнения!
6.
Таким образом, определен один из корней исходного кубического уравнения X1
= 4,
и
кроме того, известны значения (2mn)11
÷ (2mn)32
. Этих данных достаточно для
определения двух остальных корней.
6.1
Пусть (2mn)11
= 2.5 = (X
1
-
X
2
) -→ X
2
= X
1
– 2.5 = 4 – 2.5 = 1.5
. Это второй корень!
6.2
Пусть (2mn)12
= - 2.5 = (X
1
-
X
2
) -→ X
2
= X
1
+2.5 = 4 + 2.5 = 6.5. Это не корень.
6.3
Пусть (2mn)21
= 2.65 = (X
1
-
X
3
) -→ X
3
= X
1
– 2.65= 4 – 2.65 = 1.35
. Это третий корень!
Решением исходного уравнения будет X1
= 4
, X2
= 1.5,
X3
= 1.35.
Расчет закончен !
Неприводимый случай формулы Кардана
Если для кубического уравнения имеет место случай одного действительного и двух мнимых сопряженных корней, то такой вариант называют неприводимым случаем формулы Кардана.
Рассмотрим неприводимый случай формулы Кардана с позиций системы mn параметров.
Задача
"Задано кубическое уравнение вида ax3 + bx2+ cx + в = 0. Известно, что нули этого уравнения имеют один действительный и два мнимых сопряженных корня . Используя формулы системы mn параметров предложить метод определения нулей исходного уравнения ".
Пусть а = 1.
Решение
Ранее было показано, что для любого кубического уравнения имеют место формулы
D1
= - (2mn)12( 2mn)22( 2mn)32
D2
= - [(2mn)12 + ( 2mn)22 + ( 2mn)32
],
где
- (2mn)
j
- разность любой пары корней исходного уравнения
-
D1
= -

- D2
= - 2( 3c –
b
2
)
- ( b,c,d) – коэффициенты исходного уравнения.
По условиям задачи имеем один действительный корень ( обозначим его X
1
=
g
1
) и два сопряженных мнимых корня X
2
=
(
g
2
-
hi
),
X
3
= (
g
2
+
hi
).
Тогда
(2
mn
)1
= (
X
1
-
X
2
) = (g
1
-
g
2
) +
hi
(2
mn
)2
= (
X
1
-
X
3
) = (g
1
-
g
2
) –
hi
(2mn)3
= ( X2
- X3
) = g2
- hi - g2
– hi = - 2hi
-→ D1
= - ( 2mn)1
2
∙ ( 2mn)2
2
∙ ( 2mn)3
2
= - [(g1
- g2
) + hi]2
∙ [(g1
- g2
) - hi]2
∙ [2 hi]2
-→ D
1
= [(
g
1
-
g
2
)2
+
h
2
]2
∙ 4
h
2
Обратим внимание на то, что в этой формуле в квадратных скобках имеют место
- знак “ + “
- только действительные числа.
Таким образом, метод решения поставленной задачи заключается в следующем
1
. На основании значений коэффициентов исходного уравнения по формулам
D
1
= -

D
2
= - 2( 3c -
b
2
)
определяются значения D
1
и D
2
.
2.
Определяются D
1
- как произведение двух квадратов
D
2
- как удвоенная сумма
двух квадратов.
3.
Определяются значения g
1
,
g
2
,
h
.
4.
Определяются значения (2mn)11
, (2mn)21
, (2mn)31
5.
Определяются значения корней исходного уравнения.
Пример 5
Решить уравнение с помощью формул системы mn параметров
x3 -9x2 + 73x – 265 = 0
где
a =1, b = - 9, c = 73, в = - 265
В этом уравнении имеет место неприводимый случай формулы Кардана.
Решение
1. Определяем значение
D1
= - 
-→D1
= - [4(219 – 81)3+(- 1458 + 5913 – 7155)2]/27 = - [ 10512288 + 7290000]/27= - 659344
2.
Для дальнейших расчетов общий знак “ -
“ не имеет значения, поэтому будем рассматривать D1
как положительную величину.
-→D1
= [(
g
1
-
g
2
)2
+
h
2
]2
∙ 4
h
2
= 659344 = 2∙2∙2∙2∙7∙7∙29∙29 = 4∙2∙2∙7∙7∙29∙29= 4∙72
∙ 582
Здесь число 659344 представлено в виде всех сомножителей с целью наглядности формирования множителей в соответствии с формулой [(
g
1
-
g
2
)2
+
h
2
]2
∙ 4
h
2
. Тогда можно записать
h
= 7
, (g1
- g2
)2
+ h2
= 58 -→ (g1
- g2
)2
= 58 – 49 = 9 -→( g1
- g2
) = ± 3
3.
Для определения g1
и g2
воспользуемся свойством корней исходного уравнения
- b = X1
+X2
+X3
-→ - ( - 9) = g1
+ g2
+ hi + g2
– hi = g1
+ 2 g2
-→ 9 = g1
+ 2g2.
4.
Теперь, имея два уравнения ( g1
- g2
)= ± 3 и (g1
+ 2 g2
) = 9, можно определить значения g1
и g2
Пусть ( g1
- g2
)= 3 -→ g2
= g1
– 3 -→ g1
+ 2(g1
– 3) = 9 -→ 3g1
= 15 -→ g
1
= 5
-→g
2
= 2.
-→ X
1
= 5,
X
2
= 2 + 7
i
,
X
3
= 2 – 7
i
Расчет закончен !
Пример 6
Решить уравнение с помощью формул системы mn параметров
x3 -30x2 + 322x – 1168 = 0
где
a =1, b = - 30, c = 322, в = - 1168
В этом уравнении имеет место неприводимый случай формулы Кардана.
Решение
1. Определяем значение
D1
= - 
-→D1
= - [4(966 – 900)3+(- 54000 + 86940 – 31536)2]/27 = - [ 1149984 + 1971216]/27= - 115600
2.
Для дальнейших расчетов общий знак “ -
“ не имеет значения, поэтому будем рассматривать D1
как положительную величину.
-→D1
= [(
g
1
-
g
2
)2
+
h
2
]2
∙ 4
h
2
= 115600 = 2∙2∙2∙2∙5∙5∙17∙17 = 4∙2∙2∙5∙5∙17∙17= 4∙ 52
∙342
Здесь число 115600 представлено в виде всех сомножителей с целью наглядности формирования множителей в соответствии с формулой [(
g
1
-
g
2
)2
+
h
2
]2
∙ 4
h
2
. Тогда можно записать
h
= 5
, (g1
- g2
)2
+ h2
= 34 -→ (g1
- g2
)2
= 34 – 25 = 9 -→( g1
- g2
) = ± 3
3.
Для определения g1
и g2
воспользуемся свойством корней исходного уравнения
- b = X1
+X2
+X3
-→ - ( - 30) = g1
+ g2
+ hi + g2
– hi = g1
+ 2 g2
-→ 30 = g1
+ 2g2.
4.
Теперь, имея два уравнения ( g1
- g2
)= ± 3 и (g1
+ 2 g2
) = 30, можно определить значения g1
и g2
Пусть ( g1
- g2
)= - 3 -→ g2
= g1
– 3 -→ g1
+ 2(g1
– 3) = 30 -→ 3g1
= 24 -→ g
1
= 8
-→g
2
= 11.
-→ X
1
= 8,
X
2
= 11 + 5
i
,
X
3
= 2 – 5
i
Расчет закончен !
Новый метод решения кубических уравнений
Из анализа результатов вышеприведенных примеров можно предложить новый метод решения кубических уравнений..Для корней кубического уравнения могут
иметь место следующие случаи
- три корня имеют одинаковые действительные значения
- три корня имеют действительные значения, при этом два из них являются сопряженными, т.е. если X1
= g + h, то X2
= g – hили X1
= (g + h), то X2
= (g + h), то X2
=  (g – h), Наличие множителя (g – h), Наличие множителя  обусловлено численным значением коэффициента b
при X для X3
+ bX2
+ cX + в = ( X – X1
)∙( X2
+ b
X + c
) = 0. обусловлено численным значением коэффициента b
при X для X3
+ bX2
+ cX + в = ( X – X1
)∙( X2
+ b
X + c
) = 0.
- один корень имеет действительное значение, два других- комплексные и сопряженные, т.е. если X1
= g + ih, то X2
= g – ih.
Первый случай – тривиальный . (x – a )3
= x3
– 3ax2
+3a2
x – a3
= 0. Определение корней для остальных случаев является непростой задачей.
Три разных действительных корня
Пусть имеем один действительный корень ( обозначим его X
1
=
g
1
) и два сопряженных действительных корня. Если исходное уравнение разделить на разность ( X – g1
), то получим квадратное уравнение вида
[ X – (g2
+ h)]∙[ X – (g2
- h)] = 0
-→ X2
– 2g2
X + (g2
2
– h2
) = 0
-→ X1
= g1
, X2,3
= g2
± h
-→ X2
=
( g2
- h), X3
= ( g2
+ h)
-→ (2mn)1
= ( X1
- X2
) = (g1
- g2
) + h
(2mn)2
= ( X1
- X3
) = (g1
- g2
) – h
(2mn)3
= ( X2
- X3
) = g2
- h - g2
– h = - 2h
-→ D1
= - ( 2mn)1
2
∙ ( 2mn)2
2
∙ ( 2mn)3
2
= - [(g1
- g2
) + h]2
∙ [(g1
- g2
) - h]2
∙ [2h]2
-→ D1
= [(g1
- g2
)2
- h2
]2
∙ 4h2
(3)
-→ D2
= - [ (2mn)1
2
+ (2mn)2
2
+ (2mn)3
2
] = - [(g1
- g2
) + h]2
+ [(g1
- g2
) - h]2
+ 4h2
→ D2
= - [(g1
- g2
)2
+ 2(g1
- g2
)∙ h + h2
+ (g1
- g2
)2
- 2(g1
- g2
)∙ h + h2
+ 4h2
]
→ D
2
= - [ 2(
g
1
-
g
2
)2
+ 6
h
2
]
= - 2
[(
g
1
-
g
2
)2
+3
h
2
] (8)
На основании формул системы mn параметров имеем
D
1
= -
 (4) (4)
D
2
= - 2( 3c -
b
2
), (5)
где
b
,
c
,
d
-
коэффициенты исходного кубического уравнения.
Три действительных корня и два одинаковых
Пусть имеем один действительный корень ( обозначим его X
1
=
g
1
) и два равных действительных корня. Тогда имеем h
=0
и (2
mn
)
I
= 0
При (2
mn
)
I
= 0
на основании уравнения (1) будем иметь
3
x
2
+ 2
bx
+с = 0 (6)
→ X
2
=
(
g
2
-
h
),
X
3
= (
g
2
+
h
)
→ X
2
=
X
3
=
g
2
→ (2mn)1
= ( X1
- X2
) = (g1
- g2
)
(2mn)2
= ( X1
- X3
) = (g1
- g2
)
(2mn)3
= ( X2
- X3
) = g2
- g2
= 0
→ D1
= - ( 2mn)1
2
∙ ( 2mn)2
2
∙ ( 2mn)3
2
= 0
→ D2
= - [ (2mn)1
2
+ (2mn)2
2
+ (2mn)3
2
] = - [ (2mn)1
2
+ (2mn)2
2
]
→ D2
= 2 (2mn)1
2
= 2
(g1
- g2
)2
= - 2( 3c – b2
) = 2( b2
– 3c )
→ (g1
- g2
)2
= ( b2
- 3c )
На основании свойств корней исходного уравнения можно записать -
b
=
X
1
+ 2
X
2
→ g
1
+ 2
g
2
= -
b
Решая систему из двух уравнений будем иметь g
2
= -

→ X11,12
= g11,12
=
 [ - b ± [ - b ±
 ] ]
→ X
21,22
=
g
21,22
=
 [ -
b
± [ -
b
±
 ] ]
Расчет закончен !
Пример 7
Решить уравнение с помощью формул системы mn параметров
x3 -41x2 + 475x – 1083 = 0
где
a =1, b = - 41, c = 475, в = - 1083
1.
X11,12
= g11,12
=  [ - b ± [ - b ±  ] → X11,12
= ] → X11,12
=  [ 41 ± [ 41 ±  ] = ] =  [ 41 ± [ 41 ±  ] ]
→ X11
=  , X1
= 3 , X1
= 3
X21,22
= g21,22
=  [ - b ± [ - b ±  ] → g21,22
= ] → g21,22
=  [ 41 ± [ 41 ±  ]= ]=  [ 41 ± [ 41 ±  ] ]
→ X21
= 19, X22
=  → X
2
=
X
3
= 19 → X
2
=
X
3
= 19
Расчет закончен !
Вывод основных формул
Задано исходное уравнение x3 + bx2+ cx + в = 0
. Необходимо найти значения корней.
1.
Определяем значение D
1
= -

2.
Разделим 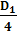
3.
Представляем число 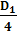 в виде произведения двух квадратов в виде произведения двух квадратов 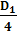 = [(
g
1
-
g
2
)2
-
h
2
]2
∙
h
2
. = [(
g
1
-
g
2
)2
-
h
2
]2
∙
h
2
.
4.
Меньший множитель принимаем за h
2
→ [(
g
1
-
g
2
)2
-
h
2
]2
=

→ (
g
1
-
g
2
) =
 (6) (6)
5. Для получения второго уравнения используем свойство корней исходного уравнения
Из исходного уравнения b = - (X1
+ X2
+ X3
) → b = - (g1
+ g2
- h + g2
+h )
→ b
= - (
g
1
+ 2
g
2
) (7)
6.
Решая систему из двух уравнений (26) и (27) в итоге получим
X1
= g1
=
 - b ) - b )
→ X11
= g11
=
 - b ) (8) - b ) (8)
→ X12
= g12
=
 - b ) (9) - b ) (9)
Таким образом получили значение одного из корней исходного уравнения.
7.
→ g2
= -
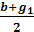
→ g21
= -

→ g
22
= -

8.
Определяем два остальных корня
X21
= g21
+ h
X22
= g22
+ h
X31
= g21
– h
X32
= g22
– h
Этими формулами определены по два варианта каждого из трех корней. Среди этих вариантов имеют место и корни исходного кубического уравнения.
Задача решена!
Пример 8
Решить уравнение с помощью формул системы mn параметров
x3 -33x2 + 311x – 663 = 0
где
a =1, b = - 30, c = 322, в = - 1168
Решение
1. Определяем значение
D1
= - 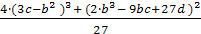
-→D1
= - [4(933 – 1089)3+(- 71874 + 92367 – 17901)2]/27 = - [- 15185664 +6718464 ]/27=313600
-→ D1
= [(
g
1
-
g
2
)2
-
h
2
]2
∙ 4
h
2
= 313600 = 4∙42
∙72
∙102
= 4∙402
∙72
= 4∙702
∙42
= 4∙282
∙102
313600 = 4∙1402
∙22
= 4∙72
∙402
= 4∙52
∙562
-→ 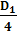 =
402
∙72
= 702
∙42
= 282
∙102
= 1402
∙22
=52
∙562 =
402
∙72
= 702
∙42
= 282
∙102
= 1402
∙22
=52
∙562
2.
Пусть
h
1
2
= 72
→ X1
= g11
=
 - b )
= - b )
=  - b) = - b) = 
→ g11
=
X11
= 13, X12
= 9.
→ g21
= -
 = - = -
 = 10 = 10
→ X
2,3
= g
21
+
h
1
= 10 ± 7 → X
2
= 17,
X
3
= 3
Задача решена!
Неприводимый случай формулы Кардана
Пусть имеем один действительный корень ( обозначим его X
1
=
g
1
) и два мнимых сопряженных корня
X
2
=
(
g
2
-
ih
),
X
3
= (
g
2
+
ih
).
-→ (2
mn
)1
= (
X
1
-
X
2
) = (g
1
-
g
2
) +
ih
(2
mn
)2
= (
X
1
-
X
3
) = (g
1
-
g
2
) –
ih
(2
mn
)3
= (
X
2
-
X
3
) = g
2
-
ih
-
g
2
–
ih
= - 2
ih
Задано исходное уравнение x3 + bx2+ cx + в = 0
. Необходимо найти значения корней.
1.
Определяем значение D
1
= -

2.
Разделим 
3.
Представляем число  в виде произведения двух квадратов в виде произведения двух квадратов  = [(
g
1
-
g
2
)2
+
h
2
]2
∙
h
2
. = [(
g
1
-
g
2
)2
+
h
2
]2
∙
h
2
.
4.
Меньший множитель принимаем за h
2
→ [(
g
1
-
g
2
)2
+
h
2
]2
=

→ (
g
1
-
g
2
) =
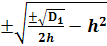
5. Для получения второго уравнения используем свойство корней исходного уравнения
Из исходного уравнения b = - (X1
+ X2
+ X3
) → b = - (g1
+ g2
- ih + g2
+ ih )
→ b = - ( g1
+ 2g2
)
6. X1
= g1
=
 - b ) - b )
→ X11
= g11
=
 - b ) - b )
→ X12
= g12
=
 - b ) - b )
7.
→ g2
= -

→ g21
= -

→ g
22
= -

8.
Определяем два остальных корня
X21
= g21
+ h
X22
= g22
+ h
X31
= g21
– h
X32
= g22
– h
Пример 9
Решить уравнение с помощью формул системы mn параметров
x3 -6x2 + 58x – 200 = 0
где
a =1, b = - 6, c = 58, в = - 200
Решение
1. Определяем значение
D1
= - 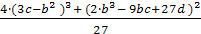
-→D1
= - [4(174 – 36)3+(- 432 + 3132 – 5400)2]/27 = - [ 10512288 + 7290000 ]/27= 659344
-→ D1
= [(
g
1
-
g
2
)2
-
h
2
]2
∙ 4
h
2
= 659344 = 4∙22
∙72
∙292
= 4∙142
∙292
= 4∙72
∙582
= 4∙22
∙2032
-→  =
2032
∙22
= 582
∙72
= 292
∙142 =
2032
∙22
= 582
∙72
= 292
∙142
Пусть
h
1
2
= 72
→ X1
= g11
=
 - b )
= - b )
=  + 6) = + 6) =  = 4 = 4
→ X1
= 4
→ g21
= -
 = - = -
 = 1 = 1
→ X2,3
= g21
+ ih1
= 1 ± 7i → X2
= 1 - 7i, X3
= 1 + 7i
Задача
решена
!
Пример 10 Дано уравнение
x3 -6x2 + 21x – 52 = 0
где
a =1, b = - 6, c = 21, в = - 52
Решить уравнение с помощью формул системы mn параметров
Решение
1. Определяем значение
D1
= - 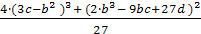
-→D1
= - [4(63 – 36)3+(- 432 + 1134 – 1404)2]/27 = - [ 78732 + 492804 ]/27= 21168
→ D1
=[(
g
1
-
g
2
)2
-
h
2
]2
∙ 4
h
2
= 21168 = 4∙22
∙72
∙  = 4∙142
∙ = 4∙142
∙ = 4∙ = 4∙
→ D1
=   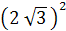
Пусть
h
1
2
=
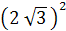
→ X1
= g11
=
 - b )
= - b )
=  + 6) = + 6) =  = 4 = 4
→ X1
= 4
→ g21
= -
 = - = -
 = 1 = 1
→ X2,3
= g21
+ ih1
= 1 ± 2i → X2
= 1 + 2i → X2
= 1 + 2i
 , X3
= 1 - 2i , X3
= 1 - 2i

Сравните метод решения и результат с первоисточником.
[И.Н.Бронштейн. К. А.Семендяев .Справочник по математике. М. Наука.1980. Стр. 220 ]
Вывод новых формул
Основные свойства корней квадратного и кубического уравнений выражаются известными формулами Виета. Использование системы mn параметров дает возможность получения новых, ранее неизвестных, формул отражающих свойства корней указанных уравнений.
Рассмотрим кубическое уравнение и проведем анализ формулы (1)
(2
mn
)2
+ ( 3
x
+
b
)(2
mn
) + 3
x
2
+ 2
bx
+с = 0
Если в это уравнение подставить значение любого из корней исходного кубического уравнения, то получим
(2
mn
)2
+ ( 3
xi
+
b
)(2
mn
) + 3
xi
2
+ 2
bxi
+с = 0
→ (2
mn
)2
+ ( 3
x
1
+
b
)(2
mn
) + 3
x
1
2
+ 2
bx
1
+с = 0
→ (2
mn
)2
+ ( 3
x
2
+
b
)(2
mn
) + 3
x
2
2
+ 2
bx
2
+с = 0
→ (2
mn
)2
+ ( 3
x
3
+
b
)(2
mn
) + 3
x
3
2
+ 2
bx
3
+с = 0
Таким образом, исходное кубическое уравнение распадается на три квадратных уравнения. При этом для каждого положительного значения (2
mn
)
I
обязательно найдется отрицательное значение (2
mn
)
j
. Поэтому общая сумма всех корней вида (2
mn
) будет равна нулю.
→ ( 3
x
1
+
b
) + ( 3
x
2
+
b
) + ( 3
x
3
+
b
) = 0
→ 3( x
1
+
x
2
+
x
3
) = - 3
b
→ ( x
1
+
x
2
+
x
3
) = -
b
.
Таким образом получили строгое доказательство одного из уравнений Виета.
Рассмотрим любых два уравнения, например,
→ (2
mn
)2
+ ( 3
x
1
+
b
)(2
mn
) + 3
x
1
2
+ 2
bx
1
+с = 0
(2
mn
)2
+ ( 3
x
2
+
b
)(2
mn
) + 3
x
2
2
+ 2
bx
2
+с = 0.
Здесь в качестве свободных членов имеем 3
x
1
2
+ 2
bx
1
+с и 3
x
2
2
+ 2
bx
2
+с. Их сумма равна
→ Σ = 3(x
1
2
+ 3
x
2
2
) + 2b
(
x
1
+
x
2
) + 2 с. Расчеты показывают, что
3(x
1
2
+x
2
2
) + 2b
(
x
1
+
x
2
) + 2 с = (
x
1
-
x
2
)2
→ (x
1
+ x
2
)2
+ b
(
x
1
+
x
2
) + с -
x
1
∙
x
2
= 0
Тогда для трех корней исходного уравнения будем иметь
→ (
x
1
+
x
2
)2
+
b
(
x
1
+
x
2
) + с -
x
1
∙
x
2
= 0
→ (
x
1
+
x
3
)2
+
b
(
x
1
+
x
3
) + с -
x
1
∙
x
3
= 0
→ (
x
2
+
x
3
)2
+
b
(
x
2
+
x
3
) + с -
x
2
∙
x
3
= 0
Это новые формулы, отражающие свойства корней исходного кубического уравнения!
В общем случае эта формула имеет вид
( xi
+ xj
)2
+ b
(
xi
+
xj
) + с -
xi
∙
xj
= 0 ( 10 )
Пример 11
Проверить формулу ( 10 )
x3 -20x2+ 113x - 154 = 0
где
a =1, b = - 20, c =113, в = -154
Здесь X
1
= 7
, X
2
= 2,
X
3
= 11.
→ (
x
1
+
x
2
)2
+
b
(
x
1
+
x
2
) + с -
x
1
∙
x
2
= 0 → (7 + 2)2
- 20( 7 + 2 ) + 113 - 7∙ 2= 0
→ (
x
1
+
x
3
)2
+
b
(
x
1
+
x
3
) + с -
x
1
∙
x
3
= 0 → (7 + 11)2
- 20( 7 + 11 ) + 113 - 7∙ 11= 0
→ (
x
2
+
x
3
)2
+
b
(
x
2
+
x
3
) + с -
x
2
∙
x
3
= 0 → (2 + 11)2
- 20( 2 + 11 ) + 113 - 2∙ 11= 0
Расчет подтверждает верность формулы ( 10 ).
Три действительных корня и два одинаковых
При наличии двух одинаковых корней имеет место нулевая разность, т.е. (2
mn
) = 0.
Тогда из уравнения (2) следует 3
x
1
2
+ 2
bx
1
+с = 0. Подставив значения коэффициентов
b
и с и решив это уравнение получим значение корня- дубля.
Пример 12
Пусть имеемв качестве исходногоуравнение x3
– 25x2
+ 203x – 539 = 0. Необходимо найти решения данного уравнения.
Решение
Допустим, что для данного уравнения имеют место два одинаковых корня. Тогда имеем 3
x
1
2
+ 2
bx
1
+с = 0 → 3
x
1
2
- 50
x
1
+ 203 = 0 →
x
1,2
=
 ) →
x
1
= ) →
x
1
=
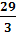 ,
x
2
= 7. ,
x
2
= 7.
Подставив значение
x
= 7 в исходное уравнение, убеждаемся, что это один из корней- дубля исходного уравнения. Определить третий корень исходного уравнения не представляет особого труда. Таким образом, решением заданного исходного уравнения является
X
1
=
X
2
= 7
, X
3
= 11
Три действительных и одинаковых корня
В этом случае имеем для всех (2
mn
) = 0.
Из уравнений (46), (47), (48) получим 3
x
1
2
+ 2
bx
1
+с = 0.
→
x
1,2
=
 ). При равенстве трех корней имеем ). При равенстве трех корней имеем  = 0 = 0
→
x
1,2,3
= -
 . .
Эту формулу можно получить и более просто. На основании формулы Виета
→
( x
1
+
x
2
+
x
3
) = -
b
. При
x
=
x
1
=
x
2
=
x
3
→ 3
x
= -
b
→
x
= -
 . .
Пример 12 Дано уравнение
x3
– 24x2
+ 183x – 448 = 0 → b= - 24, с = 183, в = - 448
Решить уравнение с помощью формул системы mn параметров
Решение
1. Определяем значение
D1
= - 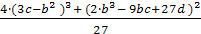
-→D1
= - [4(549 – 576)3+(- 27648 + 39528 – 12096)2]/27 = - [- 78732 + 46656 ]/27= 1188
-→ 1188= 4∙9∙33
= 4∙36∙
2.
Пусть
h
2
=
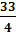
→  = [(
g
1
-
g
2
)2
-
h
2
]2
∙
h
2
→ [(
g
1
-
g
2
)2
+
h
2
]2
= 36
→[(
g
1
-
g
2
)2
-
h
2
] = ± 6 = [(
g
1
-
g
2
)2
-
h
2
]2
∙
h
2
→ [(
g
1
-
g
2
)2
+
h
2
]2
= 36
→[(
g
1
-
g
2
)2
-
h
2
] = ± 6
→ (
g
1
-
g
2
)2
= - 6 +
 = =
 → g
1
-
g
2
= ± → g
1
-
g
2
= ±
 . .
Второе уравнение
( x
1
+
x
2
+
x
3
) = -
b
→ (g
1
+
g
2
+
h
+
g
2
–
h
) = -
b
→ g
1
+ 2
g
2
= 24
Таким образом, имеем два уравнения
g
1
-
g
2
= ±
 и
g
1
= 24 - 2
g
2
. и
g
1
= 24 - 2
g
2
.
→ 24 - 2
g
2
-
g
2
= ±
 → g
2
= → g
2
=
 = =
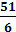 →g
2
= →g
2
=
 →g
1
= 24 - 2
g
2
→g
1
= 24 – 17
→g
1
= 7 →g
1
= 24 - 2
g
2
→g
1
= 24 – 17
→g
1
= 7
→ X
1
= 7,
X
2
=
 ( 17 + ( 17 +
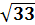 ),
X
3
= ),
X
3
=
 ( 17 - ( 17 -
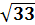 ) )
Задача решена!
Внимание! В данном примере имеет место множитель
 в значениях
X
2
и
X
3
. Этот случай
обусловлен следующим в значениях
X
2
и
X
3
. Этот случай
обусловлен следующим
1. Разделим исходное уравнение
x3
– 24x2
+ 183x – 448 = 0 на (x – 7)
→  = - x2
+ 17x – 64→ x3
– 24x2
+ 183x – 448= (x – 7)∙( x2
- 17x + 64)=0. = - x2
+ 17x – 64→ x3
– 24x2
+ 183x – 448= (x – 7)∙( x2
- 17x + 64)=0.
кубическое уравнение формула кардан
2.
В уравнении x2
- 17x + 64=0 при x имеем нечетный коэффициент равный 17. Поэтому ранее и принято значение 1188= 4∙36∙ . .
Автор с благодарностью примет конкретные предложения, замечания и оценки.
E- Mail: fgg-fil1@narod.ru
|