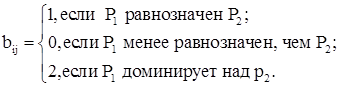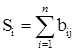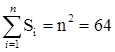Контрольная работа: Математические методы и модели

Контрольная работа

По дисциплине «Математические методы и модели»

1. Математическое моделирование задач коммерческой деятельности

Провести моделирование процесса выбора товара на основе следующих данных. Рассмотрим задачу выбора автомобиля. Составим таблицу множества показателей, по которым можно провести сравнение автомашин.

Таблица 1

Теперь необходимо сформулировать множество показателей, по которым можно провести сравнение автомобилей. Выпишем из руководства по эксплуатации автомобилей наиболее существенные показатели ( табл. 2)

Таблица 2

Сопоставим эти показатели с помощью метода парных сравнений, а результаты запишем в табл. 3, элемент которой определяется таким образом:

После заполнения матрицы элементами сравнения найдем по строкам суммы балов по каждому показателю:

где n – количество показателей, n=8

Правильность заполнения матрицы определяется равенством

Затем определяем коэффициенты весомости по формуле

Следует заметить, что

Таблица 3

Распределим коэффициент показателей по рангу R_i . На этом основании перечень потребительских характеристик будет иметь вид:

1) Ц – цена, $;

2) Рт – расход топлива на 100 км

3) МД – мощность двигателя, л.с.;

4) Ро – рабочий объем двигателя, л.;

5) V мах – максимальная скорость, км/ч.;

6) М – снаряженная масса, кг

7) Еб – емкость топливного бака, л.;

8) Дл – длина, мм

На основании полученных результатов составим таблицу бальных оценок первых четырех показателей.

Таблица 4

На основании данных табл. 4 определим значения интегральных оценок для выбранных двух более нам подходящих автомобилей:

HYUNDAI Sonata и HYUNDAI Trajet

F (HYUNDAI Sonata) = 0,234·1+0,203·2+0,141·4+0,125·5=1,83

F (HYUNDAI Trajet) =0,234·2+0,203·1+0,141·5+0,125·4=1,88

Поскольку F (HYUNDAI Trajet)> F (HYUNDAI Sonata), следует покупать автомобиль HYUNDAI Trajet.

Вывод: Сравнив множество показателей по которым мы сравнивали автомашины, получили, что F (HYUNDAI Trajet)> F (HYUNDAI Sonata), следует покупать автомобиль HYUNDAI Trajet.

2. Методы и модели линейного программирования.

Фирма производит два безалкогольных широко популярных напитка " Колокольчик" и "Буратино". Для производства 1 л. " Колокольчика требуется 0, 002 ч работы оборудования, а для " Буратино" – 0,04 ч, а расход специального ингредиента на них составляет 0,01 кг и 0, 04 кг на 1 л соответственно. Ежедневно в распоряжении фирмы 16 кг специального ингредиента и 24 ч работы оборудования. Доход от продажи 1 л

" Колокольчика" составляет 0,25 руб., а " Буратино" – 0,35 руб.

Определите ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от их продажи.

Решение:

1) Составим математическую модель данной задачи:

Пусть X₁ – количество " Колокольчиков";

Х₂ – количество " Буратино", тогда как необходимо определить ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от их продажи, то целевая функция:

F(Х₁ ,Х₂ ) = 0,25Х₁ + 0,35Х₂ мах

Система ограничений:

x_j

2) Графическое решение задачи:

Представим каждое неравенство в виде равенства, т.е имеем уравнения прямых. Построим их, тогда система ограничений запишется в виде:

1) 0,02х₁ +0,04х₂ =24

2) 0,01х₁ +0,04х₂ =16

3) х₁ =0

4) х₂ =0

Преобразуем систему неравенств ( выразим Х₂ через Х₁ )

Построим на плоскости ( х₁ ,х₂ ) область допустимых значений согласно системе неравенств

x₂ =24-0,5x₁

х₂ =16-4х₁

Многоугольником допустимых решений является треугольник АВС. Построим вектор N =

Перемещаем линию уровня перпендикулярно вектору N в направлении вектора N до опорного положения.

Вершина в которой целевая функция принимает максимальное значение это вершина

С (20;13). Следовательно, ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от продажи составляет:

f(х₁ ;х₂ )= 0,25*20+0,35*13=9,55

3) Классификация математической модели:

· По общему целевому назначению: прикладная модель;

· По степени агрегирования объектов: микроэкономическая модель;

· По конкретному предназначению: оптимизированная модель;

· По типу информации: идентифицированная модель;

· По учету фактора времени: статистическая модель;

· По учету фактора неопределенности: детерминированная модель;

· По типам математического аппарата: линейная модель;

· По типу подхода к изучаемым социально- экономическим системам: нормативная модель.

Вывод: Ежедневный план производства напитков каждого вида, обеспечивающий максимальный доход от продажи составляет 9,55 л.

3. Методы и модели теории игр

Определите максимальные стратегии игроков и седловую точку игры

Решение: Строки матрицы соответствуют стратегиям А_i (i=1,2,…,m), то есть стратегиям, которые выбирает игрок А. Столбцы – стратегии В_i ,то есть стратегии, которые выбирает игрок В.

· Игрок А выбирает такую стратегию, чтобы максимизировать свой минимальный выигрыш :

,

где а – нижняя цена игры (гарантированный выигрыш игрока А)

· Игрок В выбирает такую стратегию, при которой его максимальный проигрыш

- минимизируется:

,

где - верхняя цена игры.

Составим расчетную таблицу.

коммерческий математический моделирование линейный программирование

Этот выигрыш гарантирован игроку 1, как бы ни играл второй игрок.

Нижняя цена игры составляет 6

Минимальный проигрыш второго игрока

Получили, что первый игрок (А) должен выбрать пятую (А₄ ) стратегию, а второй игрок (В) должен выбрать четвертую (В₅ ) стратегию.

Итак, нижняя цена игры, или максимальный выигрыш: , верхняя цена игры, или минимальный выигрыш:

Нижняя и верхняя цена игры равны и достигаются на одной и той же паре стратегий

(А₄ ;В₅ ). Следовательно, игра имеет седловую точку (А₄ ;В₅ ).

Вывод: Игрок А должен выбрать четвертую стратегию, а игрок В пятую стратегию при этом выигрыш первого игрока будет максимальным из максимальных как бы ни играл второй игрок, а второй игрок минимально проиграет. Игра имеет седловую точку (А₄ ;В₅ ).