МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
«Северо-Западный Государственный Заочный Технический Университет»
Институт управления производственными и инновационными программами
Дисциплина: Статистика
контрольная работа
на тему: ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ. ИСПЫТАНИЕ СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ВЫПОЛНИЛ: студентка 5 курса ЭГФ
Группа 624
Шифр 6710210047
Лодырева М.С.
ПРОВЕРИЛ: Волков В.Ф.
Санкт-Петербург
2010
Содержание
1. Выборочное наблюдение испытание статистических гипотез
1.1 Причины применения выборочного наблюдения. Дескриптивная статистика и статистический вывод
1.2 Способы отбора, обеспечивающие репрезентативность выборки. Виды выборки
1.3 Ошибка выборки
1.4 Влияние вида выборки на величину ошибки выборки
1.5 Задачи, решаемые при применении выборочного метода
1.6 Распространение данных выборочного наблюдения на генеральную совокупность
1.7 Малая выборка
1.8 Примеры применения выборочного метода
Заключение
Приложение
выборка статистика отбор ошибка
1. Выборочное наблюдение испытание статистических гипотез
1.1 Причины применения выборочного наблюдения. Дескриптивная статистика и статистический вывод
Из всех видов несплошного наблюдения главным является выборочное наблюдение, так как только выборочный метод имеет статистако-математическое обоснование распространения данных, полученных по выборке, на всю совокупность. Причин использования выборочного метода несколько.
Во-первых, как это ни парадоксально, это повышение точности данных: уменьшение числа единиц наблюдения в выборке резко снижает ошибки регистрации. Правда, за счет неполноты охвата единиц возникает ошибка репрезентативности, т.е. представительности выборочных данных. Но даже взятые вместе ошибка наблюдения для выборки плюс ошибка репрезентативности обеспечивают большую точность выборочных данных по сравнению с массовым сплошным наблюдением. При ограниченном объеме работ можно привлечь более квалифицированных исполнителей (интервьюеров, счетчиков- регистраторов). Это положительно сказывается на качестве данных выборочного обследования.
Во-вторых, обращение к выборкам обеспечивает экономию материальных, трудовых, финансовых ресурсов и времени. Например, для составления баланса денежных доходов и расходов населения, для изучения денежного обращения, выявления дифференциации населения по уровню жизни, определения черты бедности и т.д. необходимы данные о бюджетах домохозяйств. Сбор этих данных осуществляется государственной статистикой, но один статистик в состоянии курировать ежедневные записи доходов, расходов, потребления не более чем в 20—25 домохозяйствах. Если бы он решил собирать данные о бюджетах всех домохозяйств, то только для этой цели (не учитывая потребности последующей обработки) потребовалось бы примерно два миллиона статистиков. Так что использование выборочного наблюдения является единственным экономически выгодным решением, тем более что по результатам изучения сравнительно небольшой части можно получить с достаточно высокой степенью уверенности данные о всей совокупности. Подобная ситуация возникает при аудиторских проверках крупных фирм, когда вместо детального изучения каждого платежного документа ограничиваются анализом выборки документов, и в других областях применения статистики.
В-третьих, без выборки не обойтись, когда наблюдение связано с порчей наблюдаемых объектов. Это относится прежде всего к изучению качества продукции, которое основано на испытаниях образцов на вибрацию, упругость, разрыв и т.д. Всю продукцию, конечно же, таким испытаниям не подвергают, а только отобранные образцы. То же можно сказать об исследовании молока на жирность, зерна — на содержание белка, влажность, чистоту и всхожесть семян, электрических лампочек — на длительность горения и т.д. На выборках основаны маркетинговые исследования, оценки качества поставок.
Практика применения выборочного метода очень разнообразна. Иногда, проведя сплошное наблюдение, используют выборочный метод при разработке данных: отбирают часть данных для более подробной разработки по расширенной программе. Так поступают, например, при разработке данных переписи населения о составе и типах семей. Нередко в процессе сбора данных применяют совместно сплошное и несплошное наблюдение. При переписях населения в нашей стране (1959, 1970, 1979 гг.) собирались сведения о каждом лице по 11 признакам, а 25% населения давали более подробную информацию (18 вопросов).
Выборки используются при опросах общественного мнения, при выяснении потребительских предпочтений, формировании доходов и расходов населения, при определении урожайности сельскохозяйственных культур и продуктивности скота. С 20-х гг. XX в. выборочный метод стал использоваться для контроля и анализа качества продукции. Сейчас методы статистической выборки все шире внедряются в самые различные области. В 1994 г. в Российской Федерации была проведена 5%-ная микроперепись населения с целью уточнения демографического и социального состава населения, уровня благосостояния, включая жилищные условия, источники дохода и др. Эта микроперепись была положена в основу новой бюджетной выборки, созданной в 1996 г. на период до 2003 г., после чего она должна быть пересмотрена на основе данных Всероссийской переписи населения 2002 г.
Та совокупность, из которой проводится отбор, называется генеральной совокупностью; отобранные данные составляют выборочную совокупность. Эти данные представляют интерес, поскольку дают основание для суждений о параметрах и свойствах генеральной совокупности. Таким образом, выборочный метод обладает следующими достоинствами:
• относительно небольшие (по сравнению со сплошным наблюдением) материальные, трудовые и стоимостные затраты на сбор данных (включая затраты на планирование и формирование выборки);
• оперативность получения результатов;
• широкая область применения;
• высокая достоверность результатов.
Все эти достоинства проявляются лишь при условии правильного решения проблем выборочного обследования.
К ним относятся:
1) определение границ генеральной совокупности;
2) разработка программы наблюдения и инструкций;
3) определение основы для проведения выборки — списка единиц генеральной совокупности, сведений об их размещении и т.д.;
4) установление допустимого размера погрешности и определение объема выборки;
5) определение вида выборочного наблюдения;
6) установление сроков проведения наблюдения;
7) определение потребности в кадрах для проведения выборочного наблюдения, их подготовка;
8) оценка точности и достоверности данных выборки, определение порядка их распространения на генеральную совокупность.
Представление о статистических данных, как о выборочных, может относиться не только к собственно выборке, но и к данным сплошного наблюдения, которые иногда рассматриваются как выборка из всех возможных реализаций изучаемого процесса. Это имеет смысл в случае мапого числа единиц совокупности. Кроме того, трактовка данных как выборочных используется применительно к результатам эксперимента, которые рассматриваются как некая выборка из потенциально бесконечного числа повторений экспериментальных наблюдений. Трактовка данных как выборочных является основой деления статистики на описательную (дескриптивную) и выводную. Методы описательной статистики включают сбор данных по всем единицам изучаемой совокупности, их обработку, получение сводных показателей, которые характеризуют только наблюдаемую совокупность. Например, если наша задача состоит в изучении успеваемости группы студентов, включающей 25 человек, то вычисленный средний балл по этой группе, процент отличных оценок и т.д. являются описаниями данной совокупности. Если же мы будем рассматривать эту группу студентов с точки зрения оценки успеваемости всех студентов данного колледжа или университета, то эта группа предстанет как выборка из общего числа студентов. В таком случае средний балл для группы будет являться оценкой средней успеваемости студентов колледжа в целом.
Генеральная совокупность может быть реальной, а может быть гипотетической, включающей случаи, которые реально не существуют, например, все возможные результаты эксперимента. В выводной статистике принято строго различать параметры и свойства генеральной совокупности и их оценки по данным выборки. С этой целью принята следующая система обозначений: генеральные параметры обозначаются греческими буквами, выборочные показатели, которые рассматриваются как оценки генеральных параметров, — латинскими буквами:
Подводя итоги, можно сказать, что описательная статистикаявляется инструментом описания совокупности, по которой у нас полностью имеются исходные данные. Метод статистического вывода позволяет по данным выборок делать заключение о большей совокупности, по которой мы не имеем исчерпывающих наблюдений.
1.2 Способы отбора, обеспечивающие репрезентативность выборки. Виды выборки
Для того чтобы по выборке можно было делать вывод о свойствах генеральной совокупности, выборка должна быть репрезентативной (представительной), т.е. полно и адекватно представлять свойства генеральной совокупности. Репрезентативность выборки может быть обеспечена только при объективности отбора данных. Выборочная совокупность формируется по принципу массовых вероятностных процессов, без каких бы то ни было исключений из принятой схемы отбора. Необходимо обеспечить относительную однородность выборочной совокупности, или ее разделение на однородные группы единиц. При формировании выборочной совокупности должно быть дано четкое определение единицы отбора. Желателен приблизительно одинаковый размер единиц отбора, причем результаты будут тем точнее, чем меньше единица отбора. Возможны три способа отбора: случайный отбор, отбор единиц по определенной схеме, сочетание первого и второго способов. Если отбор в соответствии с принятым способом проводится из генеральной совокупности, предварительно разделенной на типы (слои или страты), то такая выборка называется типической (или расслоенной, или стратифицированной, или районированной). Еще одно деление выборки по видам определяется тем, что является единицей отбора: единица наблюдения или серия единиц (иногда используют термин «гнездо»). В последнем случае выборка называется серийной или гнездовой. На практике часто используется сочетание типической выборки с отбором сериями. В математической статистике, обсуждая проблему отбора данных, обязательно вводят деление выборки на повторную и бесповторную.
Первая соответствует схеме возвратного шара, вторая — безвозвратного (при рассмотрении процесса отбора данных на примере отбора шаров разного цвета из урны). В социально- экономической статистике нет смысла применять повторную выборку, поэтому, как правило, имеется в виду бесповторный отбор. Если выборка проводится по схеме возвратного шара, то вероятность попадания любой единицы в выборку равна 1/N, и она остается той же самой на протяжении всей процедуры отбора. Если выборка проводится по схеме невозвратного шара, то вероятность попадания единицы в выборку изменяется последней. Поскольку социально-экономические объекты имеют сложную структуру, организовать выборку бывает довольно трудно. Например, чтобы провести отбор домохозяйств при изучении потребления населения крупного города, легче провести сначала отбор территориальных ячеек, жилых домов, потом квартир или домохозяйств, затем респондента. Такая выборка называется многоступенчатой. На каждой ступени используются разные единицы отбора: более крупные — на начальных ступенях, на последней ступени единица отбора совпадает с единицей наблюдения. Еще один вид выборочного наблюдения — многофазовая выборка. Такая выборка включает определенное количество фаз, каждая из которых отличается подробностью программы наблюдения. Например, 25% всей генеральной совокупности обследуются по краткой программе, каждая четвертая единица из этой выборки обследуется по более полной программе и т.д. При любом виде выборки отбор единиц проводится тремя отмеченными способами. Рассмотрим процедуру случайного отбора. Прежде всего составляется список единиц совокупности, в котором каждой единице присваивается цифровой код (номер или метка). Затем проводится жеребьевка. Шары с соответствующими номерами закладываются в барабан, перемешиваются, и проводится их отбор. Выпавшие номера соответствуют единицам, попавшим в выборку; число номеров равно запланированному объему выборки.
Отбор жеребьевкой может быть подвержен смещениям, вызванным недостатками техники (качеством шаров, барабана) и другими причинами. Более надежен с точки зрения объективности отбор по таблице случайных чисел. Такая таблица содержит серии цифр, чередующихся случайным образом, отобранных путем электронных сигналов. Поскольку мы пользуемся десятичной цифровой системой 0, 1,2, ..., 9, вероятность появления любой цифры равна 1/10.
Следовательно, если бы нужно было создать таблицу случайных чисел, включающую 500 знаков, то 50 из них были бы нули, столько же — единиц и т.д. Ввиду того, что каждая цифра и их последовательность являются случайными, можно использовать таблицу случайных чисел, перемещаясь либо по ее вертикали, либо по горизонтали. Цифры сгруппированы по пять для лучшей обозримости таблицы и пользования .
Пример. Предположим, что нам нужно провести 5%-ную выборку из 9540 студентов университета. Объем выборки составит: п = 5% - 7V = 477 студентов. Ввиду того, что объем генеральной совокупности выражается четырехзначным числом, код каждого студента должен быть четырехзначным: от 0001 — для первого студента до 9540 — для последнего студента в списке. Для того чтобы провести отбор по таблице случайных чисел, нужно выбрать начальную точку: можно закрыть глаза и поставить наугад точку в таблицу карандашом. Предположим, мы попали в 13-ю строку в 1-й столбец
Следовательно, единица с номером 9082 является первой в выборке. Если двигаться по строке, то единица с номером 2602 будет второй, 8088 — третьей, 9259 — четвертой. Следующий код 9610 пропускаем, так как у нас нет студента с таким номером. Далее в выборку попадают номера 4277, 2605, 6176, 8730, 4117, 7212, 1791, 5296, 5919, 0305, 1018. Код 9797 пропускается. Следующие отобранные номера 7868, 0161, 3747, 9526, 8413, 7725 и т.д.
Процедура продолжается, пока число отобранных номеров не составит требуемый объем выборки (n = 477). Часто используется отбор по какой-либо схеме (так называемая направленная выборка). Схема отбора принимается такой, чтобы отразить основные свойства и пропорции генеральной совокупности. Простейший способ — по спискам единиц генеральной совокупности, составленным так, чтобы упорядочивание единиц было бы не связано с изучаемыми свойствами, проводится механический отбор единиц с шагом, равным N: n. Обычно отбор начинают не с первой единицы, а отступив полшага, чтобы уменьшить возможность смещения выборки. Частота появления единиц с теми или иными особенностями, например студентов с тем или иным уровнем успеваемости, живущих в общежитии, и т.д., будет определяться той структурой, которая сложилась в генеральной совокупности. Для большей уверенности в том, что выборка отразит структуру генеральной совокупности, последняя подразделяется на типы, и проводится случайный или механический отбор из каждого типа. Общее число единиц, отобранных, из разных типов, должно соответствовать объему выборки. Особые трудности возникают, когда нет списка единиц, а отбор нужно провести либо на местности, либо из образцов продукции на складе готовой продукции. В этих случаях важно детально разработать схему ориентации на местности и схему отбора и следовать ей, не допуская отклонений.
Например, счетчик получает указание двигаться от определенной автобусной остановки на север по четной стороне улицы и, отсчитав два дома от первого угла, войти в третий и провести опрос в каждом пятом жилом помещении. Неукоснительное следование принятой схеме обеспечивает выполнение главного условия формирования репрезентативной выборки объективность отбора единиц.
От случайной выборки следует отличать квотный отбор, когда выборка конструируется из единиц определенных категорий (квот), которые должны быть представлены в заданных пропорциях. Например, при опросе покупателей универмага может быть запланировано провести отбор 150 респондентов, в том числе 90 женщин, из низ 25 — девушек, 20 — молодых женщин с маленькими детьми, 35 — женщин среднего возраста, одетых в деловой костюм, 10 — женщин старшего возраста; кроме того, планировался опрос 60 мужчин, из них 25 подростков и юношей, 10 — молодых мужчин с детьми, 15 —мужчин, которые одеты в костюмы, 10 — мужчин, одетых в спортивную одежду. Для определения потребительских ориентации и предпочтений такая выборка, может быть, и хороша, но если мы захотим по ней установить среднюю сумму покупок, их структуру, получим непредставительные результаты. Это происходит потому, что квотная выборка нацелена на отбор определенных категорий. Выборка может быть нерепрезентативной, даже если она формируется в соответствии с известными пропорциями генеральной совокупности, но отбор проводится без какой-либо схемы — единицы набираются, как угодно, лишь бы обеспечить соотношение их категорий в тех же пропорциях, что и в генеральной совокупности (например, соотношение мужчин и женщин, респондентов в возрасте моложе и старшетрудоспособного, в трудоспособном и т.д.).
Эти замечания должны предостеречь вас от подобных подходов к формированию выборки и еще раз показать необходимость объективного отбора.
1.3 Ошибка выборки
Все ошибки выборочного наблюдения подразделяются на ошибки выборки (случайные); ошибки, вызванные отклонением от схемы отбора (неслучайные); ошибки наблюдения (случайные и неслучайные). Плохо, когда ошибка выборки превышает допустимый размер погрешности, но слишком высокая точность также подозрительна и, как правило, свидетельствует об ошибках отбора. К неслучайным ошибкам приводят ошибки отбора. Так бывает, если объективный отбор подменяется «удобной» выборкой. Например, когда появляются добровольные респонденты — те, кто сами предлагают, чтобы их опросили. Очевидно, что характеристики таких добровольцев и недобровольцев могут быть различны и это приведет к ошибочному заключению о генеральной совокупности. Такая же опасность возникает при замене по какой-либо причине единиц, попавших в выборку, другими единицами (например, вместо отобранного домохозяйства, где в момент прихода интервьюера никто не открыл дверь, был проведен опрос в соседней квартире или интервьюер встретил решительный отказ участвовать в опросе и был вынужден пойти на замену домохозяйства). Как отмечает социолог В. И. Паниотто, систематические ошибки представляют собой некоторое постоянное смещение, которое не уменьшается с увеличением числа опрошенных и вызваны недостатками и просчетами в системе отбора респондентов. Если, например, для изучения общественного мнения жителей города в архитектурном управлении получить сведения о жилом фонде и из всех имеющихся в городе квартир отобрать случайным образом 400, а затем предложить интервьюерам опросить всех, кого они застанут в момент посещения в этих квартирах, то полученные данные не будут репрезентативны. Допущена систематическая ошибка: более подвижная часть населения попадает в выборку в меньшей пропорции, а менее подвижная — в большей пропорции, чем в генеральной совокупности.
Таким образом, с вероятностью 0,95 можно утверждать, что средняя продолжительность расчетов предприятия данного треста с кредиторами составляет не менее 26,7 дня и не более 29,7 дня. Ошибка выборки для выборочной относительной величины (доли) определяется аналогично. Дисперсию относительной величины определим по данным выборки:
Пример. По данным выборочного изучения 100 платежных документов предприятий одного треста оказалось, что в шести случаях сроки расчетов с кредиторами были превышены. С вероятностью 0,954 требуется установить доверительный интервал доли платежных документов треста без нарушения сроков:
1.4 Влияние вида выборки на величину ошибки выборки
Как указывалось в подразд. 7.2, при проведении выборочного наблюдения используются различные способы формирования выборочной совокупности: случайный отбор — повторный или бесповторный, механический, серийный, типический. Вид выборки влияет на величину ошибки выборки. При бесповторном отборе формулы средней ошибки выборки (7.4) и (7.14) дополняются множителем Величина ошибки районированной выборки меньше величины ошибки простой (нерайонированной выборки). Часто используется сочетание районированного отбора с отбором сериями. Такой вид выборки обеспечивает преимущества в организации выборки и уменьшение ошибки выборки. Дисперсия такой выборки представляет среднюю из межсерийных дисперсий для каждого у'-го района: Оборачиваемость запасов рассчитывается делением продолжительности периода (полгода) на среднюю продолжительность одного периода оборота запасов. Очевидно, что чем скорее оборачиваются запасы, тем выше их отдача.
Коэффициент покрытия рассчитывается как отношение суммы всех источников покрытия запасов к стоимости запасов. Еслизначение этого показателя меньше единицы, то текущее финансовые показатели предприятий легкой промышленности крупного города за I полугодие 2001 г. т.е. таких предприятий должно быть не меньше 2% и не больше 28%. Фактически в генеральной совокупности их оказалось 20% общего числа предприятий, т.е. выборка дает репрезентативный результат и по этому показателю.
Выполненная выборка формировалась как простая бесповторная механическая. Однако наверняка статистик будет стремиться учесть структуру генеральной совокупности, поэтому более естественной была бы выборка, учитывающая выделение предприятий разных форм собственности. Тогда выборка должна быть районированной.
Пример. Генеральная совокупность состоит из 11 государственных предприятий, 36 частных, 13 смешанных. В выборке эти пропорции соблюдаются следующим образом: отобраны по 4 предприятия государственных и смешанных и 12 частных.
Таким образом, использование многоступенчатой выборки улучшает организацию выборки, но увеличивает ее ошибку. Кроме рассмотренных применяется многофазовая выборка, когда одни сведения собираются по всем единицам выборки, а другие — только по подвыборке из первоначальной выборки.
При периодическом повторении выборочных обследований с целью изучения динамики явлений применяются либо независимые выборки — через определенные промежутки времени отбор каждый раз проводится независимо от предыдущих выборок; либо фиксированные выборки — в этом случае повторные обследования проводятся по одной и той же выборке. В связи с тем, что в фиксированной выборке могут происходить изменения (прежде всего за счет выбытия единиц), практикуют периодическую адаптацию фиксированной выборки к происходящим изменениям. Чаще для целей изучения динамики используется промежуточный вариант ротационная выборка (частичное замещение). При этом нужно следовать определенному плану замещения, например, каждый раз замещать четверть выборки, тогда каждая первоначально отобранная единица останется в четырех следующих друг за другом выборках.
Названные виды выборок ориентированы на отбор конкретных материальных явлений. Помимо них следует назвать как особыйвид выборки метод моментных наблюдений. Сущность этого метода состоит в периодической фиксации состояний наблюдаемых единиц в отобранные моменты времени. Расчет объема такой выборки дает количество моментов. Этот вид выборочного наблюдения применяется при изучении использования производственного оборудования либо рабочего времени (подразд. 7.7).
1.5 Задачи, решаемые при применении выборочного метода
При использовании выборочного метода возникают три основные задачи:
• определение объема выборки, необходимого для получения требуемой точности результатов с заданной вероятностью;
• определение возможного предела ошибки репрезентативности, гарантированного с заданной вероятностью, и сравнение его с величиной допустимой погрешности;
• определение вероятности того, что ошибка выборки не превысит допустимой погрешности. т.е. в данном случае корректировка не оказала влияния на результаты расчета. Все округления даются с превышением. Окончательный результат: должно быть опрошено 100 человек. При проектировании районированной выборки рассчитанный объем выборки распределяют пропорционально численности районов (пропорциональный отбор):
Если доля отбора меньше 5%, к формуле бесповторного отбора не переходят, так как это несущественно скажется на величине п (как это было в рассмотренном примере).
Выборка должна быть такой, чтобы выборочные показатели по всем основным характеристикам были репрезентативны. Поэтому численность выборки рассчитывают многократно исходя из допустимых ошибок разных показателей, значения которых в генеральной совокупности известны.
Например, при выборочном учете детей школьного возраста требуется определить число семей, которые надо обследовать. При этом надо учесть: а) число детей в возрасте 6—7 лет; б) число детей в возрасте 6—15 лет; в) число детей в возрасте 16—17 лет; г) среднедушевой доход (например, для решения вопроса о строительстве базы отдыха). Вычислив значение п, на основе каждой из характеристик получаем разные объемы выборки: 1200; 300; 700; 100. Обследовать необходимо 1200 семей, т.е. из рассчитанных
числен-ностей берется максимальная. При резких различиях необходимых объемов выборки для разных вопросов программы проводится многофазный отбор. В рассмотренном примере среднедушевой доход достаточно учитывать в одной из каждых 12 семей, попавших в выборку. Многофазный отбор, как правило, довольно сложно организовать, может быть нарушен принцип случайности отбора. Поэтому для обеспечения репрезентативности оказывается выгоднее затратить больше средств на учет большего числа единиц совокупности. Многофазный отбор целесообразно применять, если соотношение между рассчитанными объемами выборки по крайней мере 1 :6
Поскольку расчет необходимой численности выборки основан не на точных, а на предположительных данных о колеблемости в совокупности, надо соблюдать следующие рекомендации: абсолютную величину п округлять только вверх; долю отбора округлять только вниз, т.е. из предосторожности планировать несколько больший объем выборки, чем показывают расчеты.
Объем многоступенчатой выборки рекомендуется увеличить не менее чем на 10% рассчитанной численности, поскольку, как было показано в подразд. 7.4, многоступенчатость отбора увеличивает ошибку выборки.
После проведения выборки рассчитывают ошибки выборочных показателей (ошибки репрезентативности), которые используются для оценки результатов выборки и для получения характеристик генеральной совокупности.
Пример. На электроламповом заводе взято для проверки 100 ламп. Средняя продолжительность их горения оказалась 1420 ч со средним квадратическим отклонением 61,03 ч. Поскольку приемщика продукции интересует качество всей партии (50 тыс. электроламп), оценивают точность полученной средней.
Средняя возможная ошибка вычисленной выборочной средней:
Аналогично можно определить вероятность того, что предел ошибки доли не превысит допустимую погрешность. Оценки надежности выборочных показателей, как показано на примере, позволяют принять обоснованные решения в отношении генеральной совокупности.
1.6 Распространение данных выборочного наблюдения на генеральную совокупность
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных, полученных по выборке. При этом исходят из того, что все средние и относительные показатели, полученные по выборке, являются несмещенными и эффективными характеристиками генеральной совокупности.
Последний сомножитель не что иное, как обратная величина доли отбора, рассчитанной по значениям признака z- Значит, итоговый подсчет по генеральной совокупности можетбыть получен делением соответствующего итогового подсчета по выборке на долю отбора. При прямом расчете берется доля отбора единиц совокупности, при способе коэффициентов — доля отбора по значению какого-либо признака.
Эффективность способа коэффициентов по сравнению с методом прямого расчета зависит от того, насколько тесно связаны между собой признаки, лежащие в основе расчета коэффициента, т.е. признак, по которому подсчитывается итог, и признак, по которому определяется доля отбора. Эффект проявляется, если коэффициент корреляции между ними больше 0,8. Способ коэффициентов используется для корректировки данных сплошного наблюдения. Например, по данным переписи скота была получена величина поголовья свиней в районе 10 000, в том числе в тех хозяйствах, которые потом были.
1.7 Малая выборка
Таблицы интеграла вероятностей используются для выборок большого объема из бесконечно большой генеральной совокупности. Но уже при п < 100 возникает несоответствие между табличными данными и вероятностью предела; при п < 30 погрешность становится значительной. Несоответствие обусловлено главным образом характером распределения единиц генеральной совокупности. При большом объеме выборки особенность распределения в генеральной совокупности не имеет значения, так как распределение отклонений выборочного показателя от генеральной характеристики при большой выборке всегда оказывается нормальным.
В выборках небольшого объема п < 30 характер распределения генеральной совокупности сказывается на распределении ошибок выборки. Поэтому для расчета ошибки выборки при небольшом объеме наблюдения (уже менее 100 единиц) отбор должен проводиться из совокупности, имеющей нормальное распределение.
1.8 Примеры применения выборочного метода
Потребность в использовании выборочного метода, выработке вероятностных суждений в современной отечественной практике непрерывно расширяется. В государственной статистике основными направлениями использования выборочного метода традиционно являются бюджетные обследования домо-хозяйств, выборочные переписи населения, контрольные обходы и проверки после проведения сплошных обследований. Создание ЕГРПО, в котором фиксируются все хозяйствующие субъекты на территории Российской Федерации всех форм собственности, открывает возможность проведения разнообразных выборочных обследований в области экономики.
В области социальных исследований для государственной статистики главным является бюджетное обследование, которое охватывает примерно 45 тыс. домохозяйств. Оно основано на многоступенчатом отборе. Общий объем выборки распределяется по сферам занятости (для работающих) и территориям. Затем для работающих проводится отбор предприятий в пределах каждой отрасли в отобранной территории. Если, например, нужно отобрать 100 рабочих, занятых в определенной отрасли, для обследования семейных бюджетов так, чтобы на каждом отобранном предприятии было не менее 20 бюджетов, включающих рабочих с разным уровнем заработной платы, то, значит, должно быть отобрано: 100 : 20 = 5 предприятий. Отбор предприятий проводят по списку, в котором предприятия располагаются в порядке убывания средней заработной платы рабочих, указываются общее число рабочих, их суммарная заработная плата. Шаг отбора определяется делением общего числа рабочих на предприятиях данной отрасли на число отбираемых предприятий. Если всего на предприятиях данной отрасли в области занято 30525 человек, то шаг отбора равен: 30525 : 5 = 6105. По данным кумулятивной численности рабочих с рассчитанным шагом отбора проводится отбор предприятий, которые затем проверяются на репрезентативность по показателю средней месячной заработной платы. Следующая стадия связана с отбором рабочих на выбранных предприятиях: среди 20 бюджетов должны быть пропорционально представлены бюджеты семей малоквали- фицированных и высококвалифицированных рабочих, а среди этих категорий отбор проводится механически по спискам рабочих, составленным в порядке убывания средней месячной заработной платы, Выборочная совокупность при бюджетных обследованиях включает и семьи неработающих (пенсионеров, студентов, инвалидов) и одиночек.
Задачей статистики в области бюджетных обследований являются обеспечение представительства всех социальных групп и учет всех источников дохода. Наиболее общим показателем уровня благосостояния населения являются денежные доходы, поступающие в семью в виде заработной платы, премий, единовременных выплат, гонораров, предпринимательского дохода или дохода от собственности, компенсационных выплат и дотаций. В совокупные доходы семьи включаются также натуральная оплата труда, доходы, полученные от реализации и потребления продукции личного подсобного хозяйства (садового участка, коллективного огорода). Для характеристики обеспеченности семей следует учитывать их накопления, а также валютные поступления. Возрастает значение анализа личного потребления. Для изучения структуры рабочего времени работников разных категорий, особенно рабочих, а также для характеристики использования машин и оборудования используется метод моментных наблюдений. Этот метод состоит в регистрации вида затрат времени в определенные, заранее выбранные моменты. Предварительно составляется список всех возможных состояний или видов затрат времени. Подсчитывается доля отметок о каждом состоянии, и оценивается доверительный интервал доли времени, затраченного на тот или иной вид работы. Отбор моментов выборки может быть проведен либо по схеме механической выборки — через равные промежутки времени, либо по схеме случайной выборки с использованием таблицы случайных чисел. Необходимая численность моментов наблюдения рассчитывается как Если при проверке отобранных документов ошибок не обнаружено, то с принятой доверительной вероятностью мы можем распространить результаты выборки на всю генеральную совокупность и считать, что итог по генеральной совокупности завышен не более чем на величину предельно допустимой ошибки. Если же обнаружена по крайней мере одна ошибка, то первоначальная гипотеза относительно отсутствия ошибок, которая закладывалась при планировании выборки, оказывается несостоятельной. В этом случае должны быть пересмотрены либо значение коэффициента надежности, либо величина предельно допустимой ошибки (точность), либо и то, и другое. Если ошибки выявлены в операциях, значение которых превышает величину шага отбора, то можно быть уверенным в отношении абсолютного размера ошибок в таких операциях, так как каждая из них проверялась полностью. В этом случае нужно решить вопрос о распространении абсолютного размера выявленных ошибок на операции, значение которых меньше шага отбора. Все ошибки группируются в два класса: завышение суммы и ее занижение. Для всех операций, значение которых превышает шаг отбора, выявленная ошибка является точным размером завышения или занижения. Для операций, значение которых меньше шага отбора, размер выявленной ошибки относится к значению операции, и полученная относительная ошибка умножается на шаг отбора, т.е. распространяется на весь интервал. После определения суммарного размера ожидаемой ошибки по всем интервалам выборки (т.е. шагам отбора) проводится сравнение с допустимым размером суммарной ошибки, и если рассчитанная суммарная ошибка превосходит допустимую величину, то, подставляя последнюю в формулу объема выборки, определяют, с каким коэффициентом надежности и соответственно с какой доверительной вероятностью могут гарантироваться результаты данного выборочного исследования: данных не в целом по единице наблюдения, а лишь по некоторым пунктам формуляра наблюдения. К частичным пропускам относят также ошибочные и некорректные ответы, которые могут быть внесены в бланк с данными в силу непонимания вопроса, неточности или просто невнимательности. Для обработки полных не ответов респондентов совокупность не ответивших предприятий должна быть разделена на три следующие группы:
• • первая — предприятия, данные по которым восстанавливаться не будут. К ним относятся предприятия, ликвидированные или находящиеся в стадии ликвидации, так называемые спящие, т.е. приостановившие свою деятельность в силу различных причин;
• • вторая — предприятия, о которых достоверно известно, что они, несмотря на отсутствие отчета, активны, ведут финансово-хозяйственную деятельность;
• • третья — предприятия, по которым нет никаких данных и даже сведений, действующие они или нет. К каждой группе полных неответов применяется свой метод коррекции и восстановления данных. Используются следующие методы восстановления пропусков:
• • заполнение с пристрастным подбором;
• заполнение по предыдущему значению;
• заполнение без подбора;
• • заполнение средними;
• • заполнение с помощью регрессии;
• замена.
Заполнение с пристрастным подбором означает поиск данных, относящихся к единицам определенного типа. Заполнение по предыдущему значению часто используется в современной практике. Но этот метод не рекомендуется применять при большом количестве пропусков, а также при наличии тенденции изменения показателя и значительном сроке со дня последней регистрации значения. Заполнение безусловными средними. По имеющимся наблюдениям рассчитываются средние, и существующий пропуск заполняется средними значениями. Этот метод эффективен при однородности анализируемой совокупности и небольшом количестве пропусков.
Заполнение с помощью регрессии состоит в заполнении пропусков значениями, предсказываемыми регрессией пропущенных для данного объекта переменных на основе присутствующих. Регрессия вычисляется по объектам с полной информацией. Этот метод выдвигает ряд серьезных требований к данным: однородность, поскольку известно, что при использовании метода наименьших квадратов небольшое число грубых ошибок может весьма существенно исказить значение характеристики распределения; подчинение теоретическому нормальному распределению, что требует дополнительной обработки информации.
5. Досчет на вновь зарегистрированные предприятия. Записи о вновь зарегистрированных предприятиях добавляются к выборочной совокупности, и коэффициент увеличения численности используется как коэффициент досчета по всем показателям.
6. Распространение результатов выборочного наблюдения на генеральную совокупность проводится по методике, рассмотренной выше.
7. Анализ и экспертная корректировка полученных результатов. За качество передаваемой на федеральный уровень информации отвечает соответствующая территория (субъект РФ или федеральный округ). Достоверность отчетности зависит только от квалификации исполнителя и желания добросовестно сделать свою работу. Решению проблем, связанных прежде всего с проблемами организации и проведения выборочных обследований малых предприятий на региональном уровне, посвящена разработка подпроекта Программы TACIS «Статистика-3». Особое внимание уделялось вопросам подготовки анкеты выборочного наблюдения, составу и структуре содержащихся в ней показателей, а также концепциям формирования выборки на региональном уровне. Большая проблема для российской статистики состоит в выявлении и обработке данных нетипичных единиц наблюдения. Несмотря на достаточно эффективный план выборки проводимого обследования, при детальном анализе данных на региональном и федеральном уровнях неоднократно выявлялись единицы, включение (или исключение) которых в выборочную совокупность сильно влияет на итоговое значенительным контролем при разработке итогов обследований малых предприятий.
Выборочный метод широко используется при проведении конъюнктурных опросов. Конъюнктурные опросы рекомендуется проводить по постоянной выборке, т.е. по панели предприятий. Это обеспечивает существенные преимущества при организации опросов и анализе результатов. Достоинства панельной организации опросов. Во-первых, регулярное получение ответов от одной и той же совокупности предприятий создает уникальную возможность экономического анализа на микроуровне.
Во-вторых, при разумной и дальновидной организации хранения и накопления результатов панельных опросов появляется возможность многократного и всестороннего использования результатов опросов. При этом аналитические результаты могут быть получены без проведения новых опросов, а только за счет применения новых методов или моделей к уже накопленным данным. Новые опросы на той же панели могут в этом случае проводиться для расширения уже существующих первичных данных.
В-третьих, регулярный (ежемесячный или ежеквартальный) характер бизнес-обследований позволяет организаторам при необходимости регулярно совершенствовать вопросы анкеты и получать таким образом все более точные данные об исследуемых явлениях.
В-четвертых, создание панели и накопление панельных данных позволяют использовать специфические статистические методы и эконометрические модели, не применимые к другим типам данных. Эти методы и модели способны обеспечить получение принципиально новых результатов.
В настоящее время на регулярной основе проводятся обследования предпринимательских намерений в промышленности, строительстве, сельском хозяйстве, оптовой торговле, а также в банковском и страховом секторах и в инновационной сфере.
Обследования базовых предприятий промышленности проводятся ежемесячно; по промышленности в целом — ежеквартально; строительных организаций, оптовой торговли и в инновационной сфере — ежеквартально; в банковском и страховом секторах — два раза в год.
Выборочное наблюдение широко используется при изучении качества готовой продукции. Отбор готовых изделий для установления их качества проводится главным образом механически (5-е, 10-е, 15-е изделие и т.д.). Если изделия в таре, то в большинстве случаев осуществляется серийный отбор (единица отбора = единице тары). Это так называемый приемочный или последующий контроль, основанный на проверке качества уже выработанных изделий; он не в состоянии предупредить появление брака.
Большое распространение получил непрерывный текущий статистический контроль за качеством изготовляемой продукции, осуществляемый в форме отбора проб в ходе производственного процесса непосредственно у рабочих мест.
Такой контроль обеспечивает систематическое наблюдение не только за качеством продукции, но и за самим производственным процессом. Текущий контроль в ходе отбора и анализа проб позволяет своевременно обнаружить неполадки в работе, сигнализировать о них и тем самым предупредить возникновение брака.
Значительной сферой применения выборочного наблюдения являются маркетинговые исследования, проводимые с целью оценки мощности рынков товаров и услуг, определения специфических сегментов рынка.
Заключение
Выборочное наблюдение проводится с целью повышения точности и оперативности данных, экономии материальных, трудовых и финансовых ресурсов.
Для того чтобы по выборке можно было делать вывод о свойствах генеральной совокупности, выборка должна быть репрезентативной. Репрезентативность выборки может быть обеспечена объективным отбором данных. Используют три способа отбора: случайный, механический, сочетание первого и второго способов.
Если отбор проводится из генеральной совокупности, предварительно разделенной на типы (районы, слои или страты), то такая выборка называется типической (районированной, расслоенной или стратифицированной).
Единицей отбора может быть единица наблюдения или группа единиц. В последнем случае выборка называется серийной или гнездовой. В социально-экономических исследованиях используется схема бесповторной выборки.
Ошибки выборочного наблюдения подразделяются на случайные и неслучайные. Случайные ошибки подчиняются вероятностным законам. К случайным относится ошибка выборки, называемая ошибкой репрезентативности.
Рассчитываются ошибки выборки для выборочных средних и выборочных относительных величин. На величину ошибки выборки влияет вид выборки: если районы существенно отличаются друг от друга, то ошибка районированной выборки будет меньше, чем нерайонированной выборки; применение гнездовой выборки при прочих равных условиях приводит к увеличению ошибки выборки. На практике часто используют сочетание районированной выборки с гнездовым отбором. Применение выборочного метода связано с решением трех задач:
• определение объема выборки, обеспечивающего требуемую точность результатов с принятой вероятностью;
• расчет предельной ошибки репрезентативности, гарантированный с принятой вероятностью, и сравнение его с величиной допустимой погрешности;
• определение вероятности того, что ошибка выборки не превысит допустимой погрешности.
Первая задача связана с распространением данных выборки на генеральную совокупность. На основе выборочных характеристик даются интервальные оценки генеральных параметров. Могут быть получены и оценки значения подсчетов в генеральной совокупности.
Определенные особенности имеют организация и проведение малых выборок (при п < 30 единиц). Выборочный метод все шире применяется как в официальной статистике, так и в научных исследованиях, и в бизнесе.
Приложение
Задача № 1
Для определения скорости расчетов с кредиторами предприятий одного треста была проведена случайная выборка 50 платежных документов, по которым средний срокперечисления денег оказался равен 28,2 дня со стандартнымотклонением 5,4 дня. Определим средний срок прохождениявсех платежей в течение данного года с доверительной вероятностью F(t)= 0,95, Тогда t= 1,96; скорректированная дисперсия средняя ошибка выборки


Отклонение выборочной средней от генеральной с вероятностью 0,95 составит; 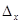 = 1,96 x 0,77 = ±1,51 дня. = 1,96 x 0,77 = ±1,51 дня.
Величина 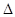 называется доверительной ошибкой выборкиили предельной ошибкой выборки. Рассчитав величину называется доверительной ошибкой выборкиили предельной ошибкой выборки. Рассчитав величину 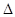 , мыможем записать следующее неравенство: , мыможем записать следующее неравенство:
28,2 - 1,51 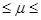 28,2 + 1,51; 28,2 + 1,51;
26,7 дня 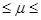 29,7 дня. 29,7 дня.
Таким образом, с вероятностью 0,95 можно утверждать, что средняя продолжительность расчетов предприятия данного треста с кредиторами составляет неменее26,7дняинеболее29,7дня.
Задача № 2
По данным выборочного изучения 100 платежных документов предприятий одного треста оказалось, что в шести случаях сроки расчетов с кредиторами были превышены. С вероятностью 0,954 требуется установить доверительный интервал доли платежных документов треста без нарушения сроков:



Генеральная доля платежных документов 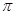 , не выходящихза установленные сроки, с вероятностью 0,954 находится винтервале , не выходящихза установленные сроки, с вероятностью 0,954 находится винтервале
0,892 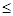 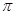 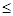 0,988, или 89,2% 0,988, или 89,2% 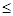 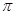 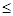 98,8%. 98,8%.
Задача №3
Для изучения интенсивности труда было организовано наблюдение за 10 отобранными рабочими. Доля работавших все время была равном 0,40, дисперсия; 0,4 • 0,6 = 0,24, По табл. П,2 приложения находим; F(t) = 0,95 и d.f. = n - 1 = 9, t=2,26. Рассчитаем среднюю ошибку выборки доли работавших все время:

Тогда предельная ошибка выборки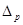 =2,26 • 0,16 = ±0,36. Таким образом, с вероятностью 0,95 доля рабочих, работавших без простоев, в данном цехе предприятия находится в пределах 4% =2,26 • 0,16 = ±0,36. Таким образом, с вероятностью 0,95 доля рабочих, работавших без простоев, в данном цехе предприятия находится в пределах 4% 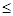 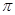 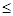 72%. 72%.
Если бы мы использовали для расчета доверительных границ генерального параметра таблицу интеграла вероятностей, тоtбыло бы равно 1,96 и 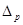 = ±0,31, т.е. доверительный интервал был бы несколько уже, но тем не менее неопределенность оценки очень велика. Следовательно, в данном случае малая выборка такого объема нецелесообразна. = ±0,31, т.е. доверительный интервал был бы несколько уже, но тем не менее неопределенность оценки очень велика. Следовательно, в данном случае малая выборка такого объема нецелесообразна.
Список литературы
1.И.И.Елисеева, М.М.Юзбашев ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ Под редакцией члена-корреспондента Российской Академии наук И.И.Елисеевой ПЯТОЕ ИЗДАНИЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ Рекомендовано Министерством образования Российской Федерации в качестве учебника для студентов высших учебных заведений, обучающихся по направлению и специальности "Статистика" Москва "Финансы и статистика" 2004г.
|