Задача № 1
Имеются следующие данные 25 предприятий легкой промышленности по величине балансовой прибыли и объему произведенной продукции:
Таблица 1.1
| № предприятия |
Объем произведенной продукции, млн. руб. |
Валовая прибыль,млн. руб. |
| 1 |
653 |
45 |
| 2 |
305 |
11 |
| 3 |
508 |
33 |
| 4 |
482 |
27 |
| 5 |
766 |
55 |
| 6 |
800 |
64 |
| 7 |
343 |
14 |
| 8 |
545 |
37 |
| 9 |
603 |
41 |
| 10 |
798 |
59 |
| 11 |
474 |
28 |
| 12 |
642 |
43 |
| 13 |
402 |
23 |
| 14 |
552 |
35 |
| 15 |
732 |
54 |
| 16 |
412 |
26 |
| 17 |
798 |
58 |
| 18 |
501 |
30 |
| 19 |
602 |
41 |
| 20 |
558 |
36 |
| 21 |
308 |
12 |
| 22 |
700 |
50 |
| 23 |
496 |
29 |
| 24 |
577 |
38 |
| 25 |
688 |
49 |
С целью изучения зависимости между объемом произведенной продукции и валовой прибылью произведите группировку предприятий по объему произведенной продукции (факторный признак), образовав пять групп предприятий с равными интервалами.
По каждой группе и совокупности предприятий подсчитайте:
1) число предприятий;
2) объем произведенной продукции – всего и в среднем на одно предприятие;
3) валовую прибыль – всего и в среднем на одно предприятие.
Результаты представьте в виде групповой таблицы. Сделайте краткие выводы.
Решение:
1. Произведем группировку предприятий по объему произведенной продукции (факторный признак), образовав пять групп предприятий с равными интервалами.
1) Определим размах вариации: R = Xmax- Xmin = 800-305 = 495
2) Длина интервала: 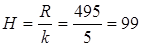
Группировку произведем в таблице 1.2.
Таблица 1.2
| № п/п |
Группы |
№ банка |
Объем произведенной продукции, млн. руб. |
Валовая прибыль, млн. руб. |
| средний |
средняя |
| 1 |
305-404 |
2 |
305 |
339,5 |
11 |
15 |
| 21 |
308 |
12 |
| 7 |
343 |
14 |
| 13 |
402 |
23 |
| Итого:
|
4
|
1358
|
60
|
| 2 |
405-503 |
16 |
412 |
473,0 |
26 |
28 |
| 11 |
474 |
28 |
| 4 |
482 |
27 |
| 23 |
496 |
29 |
| 18 |
501 |
30 |
| Итого:
|
5
|
2365
|
140
|
| 3 |
504-602 |
3 |
508 |
557,0 |
33 |
36,667 |
| 8 |
545 |
37 |
| 14 |
552 |
35 |
| 20 |
558 |
36 |
| 24 |
577 |
38 |
| 19 |
602 |
41 |
| Итого:
|
6
|
3342
|
220
|
| 4 |
603-701 |
9 |
603 |
657,2 |
41 |
45,6 |
| 12 |
642 |
43 |
| 1 |
653 |
45 |
| 25 |
688 |
49 |
| 22 |
700 |
50 |
| Итого:
|
5
|
3286
|
228
|
| 5 |
702-800 |
15 |
732 |
778,8 |
54 |
58 |
| 5 |
766 |
55 |
| 10 |
798 |
59 |
| 17 |
798 |
58 |
| 6 |
800 |
64 |
| Итого:
|
5
|
3894
|
290
|
| Всего:
|
25
|
14245
|
938
|
Выводы:
Разбив на 5 групп по объему произведенной продукции банки получили, что:
1. Самая многочисленная группа 3, с количеством входящих в неё шести банков, самая малочисленная – 1, в неё входит 4 банка.
2. По объему произведенной продукции в общем и среднем, валовой прибыли и средней валовой прибыли на одно предприятие лидирует пятая группа, а первая – наименее эффективна.
Данные показывают, что при увеличении объема произведенной продукции валовая прибыль увеличивается. Следовательно, между исследуемыми признаками существует прямая корреляционная зависимость.
Имеются следующие данные по двум заводам, вырабатывающим однородную продукцию:
Таблица 2.1
| Номер завода |
Январь |
Февраль |
| затраты времени на единицу продукции, час |
изготовлено продукции, шт |
затраты времени на |
| единицу продукции, час |
всю продукцию, час |
| 1 |
2 |
160 |
1,8 |
420 |
| 2 |
2,8 |
180 |
2,4 |
440 |
Вычислите средние затраты времени на изготовление единицы продукции по двум заводам в январе и феврале. Укажите виды средних величин, используемых в решении задач.
Решение:
Для января статистические данные представлены количеством выпущенной продукции и затратами времени на выпуск единицы продукции, поэтому средние затраты времени на изготовление единицы продукции определяем по формуле средней арифметической взвешенной:
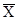 = = 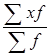 , ,
где х - затраты времени на единицу продукции, час.
f - изготовлено продукции, шт.
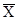 = = 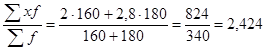 час. час.
Для февраля статистические данные представлены затратами времени на весь выпуск продукции и затратами времени на выпуск единицы продукции, поэтому средние затраты времени на изготовление единицы продукции определяем по формуле средней гармонической взвешенной:
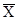 = = 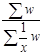 , ,
где w – объем признака, равный произведению вариант на частоты: w = x f.
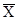 = = 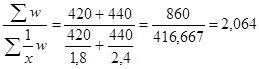
На заводе №1 в январе затраты времени на единицу продукции были снижены с 2 до 1,8 часа. На заводе №2 в 1993 г. затраты времени на единицу продукции были снижены с 2,8 до 2,4 часа.
В среднем по двум заводам затраты времени снизились с 2,424 до 2,0,64 часа, что практически обусловлено снижением эффективности производства на заводах.
В целях изучения стажа рабочих одного из цехов завода проведена 10%-ная механическая выборка, в результате которой получено следующее распределение рабочих по стажу работы:
Таблица 3.1
| Стаж рабочих, лет |
Число рабочих, чел |
До 5
От 5 до 10
От 10 до 15
От 15 до 20
От 20 до 25
Свыше 25
|
5
10
35
25
15
10
|
| Итого |
100 |
На основании этих данных вычислите:
1. Средний стаж рабочих цеха.
2. Средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих цеха.
5. С вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа рабочих со стажем работы от 10 до 20 лет.
Сделайте выводы.
Решение:
Для вычисления средней величины в каждой группе определяем серединное значение (середину интервала), после чего определяем средний стаж рабочих цеха по формуле средней арифметической взвешенной.
В закрытом интервале серединное значение определяем как полусумму верхней и нижней границ, открытые интервалы приравниваются к рядом стоящим. Кроме того, для расчёта дисперсии последовательно определяем отклонение каждой группы от средней, квадрат отклонения и произведение квадрата отклонения на число работников в группе. Расчёт производим в таблице 3.2.
Таблица 3.2
Расчет среднего квадратического отклонения
| Стаж рабочих, лет |
Число рабочих, чел. f |
х |
xf |
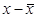 |
(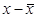 )2 )2 |
(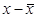 )2 f )2 f |
| До 5 |
5 |
2,5 |
12,5 |
-13,25 |
175,563 |
877,813 |
| 5-10 |
10 |
7,5 |
75 |
-8,25 |
68,0625 |
680,625 |
| 10-15 |
35 |
12,5 |
437,5 |
-3,25 |
10,5625 |
369,688 |
| 15-20 |
25 |
17,5 |
437,5 |
1,75 |
3,0625 |
76,5625 |
| 20-25 |
15 |
22,5 |
337,5 |
6,75 |
45,5625 |
683,438 |
| св. 25 |
10 |
27,5 |
275 |
11,75 |
138,063 |
1380,63 |
| Итого:
|
100
|
- |
1575
|
- |
- |
4068,75
|
1. Определим средний стаж рабочих цеха:
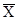 = = 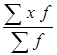 = = 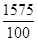 = 15,75 лет. = 15,75 лет.
2. Определим среднее квадратическое отклонение:
σ = 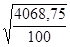 = 6,379 лет. = 6,379 лет.
Дисперсия признака σ2 = 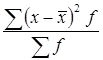 = 40,688 лет. = 40,688 лет.
3. Определим коэффициент вариации
V = 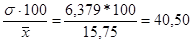 % %
4. Определим с вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих цеха.
Так как выборка механическая, то ошибка выборочного наблюдения определяется по формуле:
Δх = t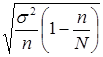
При 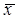 = =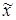 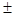 3μ и p = w 3μ и p = w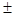 3μ степень вероятности повышается до 0,997. 3μ степень вероятности повышается до 0,997.
Таким образом:
t = 3
σ2= 40,688 - дисперсия признака;
n = 15,75 - средний стаж рабочих цеха;
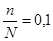 - это 10%-ная механическая выборка. - это 10%-ная механическая выборка.
Δх = t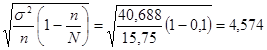
Доверительные интервалы для средней будут равны:
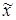 – Δх – Δх 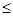 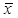 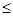 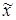 + Δх . + Δх .
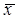 =15,75 лет. =15,75 лет.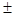 4,574 года. или 15,75-4,57 4,574 года. или 15,75-4,57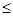 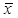 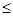 15,75+4,57 15,75+4,57
С вероятностью 0,997 можно утверждать, что средний стаж рабочих цеха находится в пределах от 11,18 дней до 20,32 дней.
5. Определим с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа рабочих со стажем работы от 10 до 20 лет.
Средняя ошибки для выборочной доли при бесповторном способе отбора рассчитывается по формуле:
Δw = t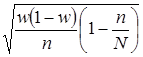 . .
При 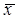 = =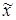 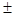 3μ и p = w 3μ и p = w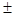 3μ степень вероятности повышается до 0,997. 3μ степень вероятности повышается до 0,997.
Таким образом:
t = 3;
n = 100 - численность рабочих цеха;
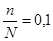 - это 10%-ная механическая выборка; - это 10%-ная механическая выборка;
Определим w - удельный вес числа рабочих со стажем работы от 10 до 20 лет.
25+35
=0,6 или 60%,
100
т.е. доля рабочих со стажем работы от 10 до 20 лет – 60%.
Δw = t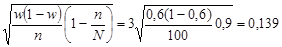 или 13,9%. или 13,9%.
Доверительные интервалы для доли будут равны:
p = w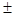 Δw . Δw .
p = 60% 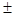 13,9%, тогда 60% – 13,9% 13,9%, тогда 60% – 13,9%  p p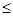 60% + 13,9%. 60% + 13,9%.
Доля числа рабочих со стажем работы от 10 до 20 лет будет находиться в пределах от 46,1 до 73,9% при вероятности 0,997.
Задача № 4
Численность населения России характеризуется следующими данными:
Таблица 4.1
| Годы |
На начало года, тыс. чел |
1997
2002
2003
2004
2005
2006
2007
|
148041
148306
147976
147502
147105
146388
145500
|
Для анализа численности населения России за 2002-2007 гг. определите:
1. Абсолютные приросты, темпы роста и темпы прироста по годам и к 2002 году.
Полученные показатели представьте в таблице.
2. Среднегодовую численность населения России.
3. Среднегодовой темп роста и прироста численности населения России за 2002-2007 гг. и за 1997-2002 гг.
Постройте график динамики численности населения России.
Сделайте выводы.
Решение:
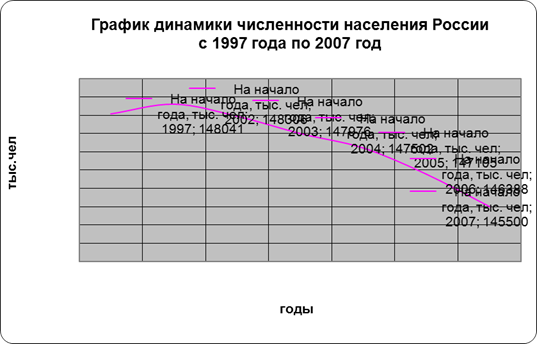
1. Определим абсолютные приросты, темпы роста и темпы прироста по годам и к 2002 году. Полученные показатели представим в таблице 4.2.
Таблица 4.2
Абсолютные приросты, темпы роста и темпы прироста
| Годы |
На начало года, тыс. чел
уi
|
Абс. приросты, млн.тонн |
Темпы роста |
Темпы прироста, % |
| цепные |
базисные (к 2002г) |
цепные |
базисные (к 2002г) |
цепные |
базисные (к 2002г) |
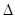 yц = уi
–
yi
-
1 yц = уi
–
yi
-
1 |
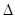 yб = yб =
уi
–
y2002
|
k = 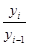 |
k = 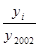 |
Δkц =
kц % – 100
|
Δkб =
k % – 100
|
| 1997 |
148041 |
265 |
-265 |
1,002 |
0,998 |
0,2% |
-0,2% |
| 2002 |
148306 |
- |
- |
- |
- |
- |
- |
| 2003 |
147976 |
-330 |
-330 |
0,998 |
0,998 |
-0,2% |
-0,2% |
| 2004 |
147502 |
-474 |
-804 |
0,997 |
0,995 |
-0,3% |
-0,5% |
| 2005 |
147105 |
-397 |
-1201 |
0,997 |
0,992 |
-0,3% |
-0,8% |
| 2006 |
146388 |
-717 |
-1918 |
0,995 |
0,987 |
-0,5% |
-1,3% |
| 2007 |
145500 |
-888 |
-2806 |
0,994 |
0,981 |
-0,6% |
-1,9% |
2. Определим среднегодовую численность населения России за 2002-2007 гг.:
За 2002-2007 гг. мы имеем интервальный ряд динамики с равными интервалами. Поэтому среднегодовую численность населения исчислим по формуле средней арифметической простой:
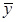 = =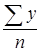 = =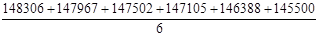 = =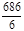 = =
147129,5тыс.чел.
где у
– уровни ряда
n
– число уровней ряда.
3. Среднегодовой темп роста и прироста численности населения России за 2002-2007 гг.
Среднегодовой темп роста исчисляется по формуле средней геометрической из цепных коэффициентов роста:
=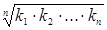 = =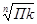 , ,
где n
– число цепных темпов роста;
за 2002-2007 гг.: =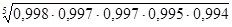 = =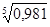 =0,996 или 99,6%. =0,996 или 99,6%.
Среднегодовой темп роста численности населения России за 2002-2007 гг. равен 99,6 %.
Среднегодовой темп прироста за 2002-2007 гг. исчисляется следующим образом:
Δ = % – 100%=99,6–100=0,4%.
Таким образом, численность населения России за период 2002-2007 гг. уменьшалось за год в среднем на 0,4%.
Выводы:
численность населения России по данным таблицы 4.1. в 2002 году повысилась по сравнению с 1997 годом на 265 тыс.чел. или на 0,2%. Затем вплоть до 2007 года снижалось в среднем на 0,4% за год.
Задача № 5
Имеются следующие данные о стоимости имущества предприятия (млн. руб.):
Таблица 5.1
| 01.01. |
01.02. |
01.03. |
01.04. |
01.05. |
01.06. |
01.07. |
| Стоимость имущества, млн. руб. |
62 |
68 |
65 |
68 |
70 |
75 |
78 |
Определите среднегодовую стоимость имущества:
1) за I квартал;
2) за II квартал;
3) за полугодие в целом.
Решение:
Среднегодовая стоимость имущества рассчитывается по формуле средней арифметической простой:
За I квартал: 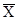 = = 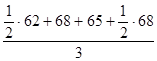 = 66 млн. руб. = 66 млн. руб.
За II квартал: 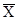 = = 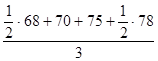 = 72,667 млн. руб. = 72,667 млн. руб.
За полугодие в целом: 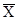 = = 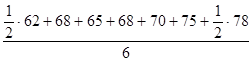 = 69,333 млн. руб. = 69,333 млн. руб.
Задача № 6
Динамика средних цен и объема продажи на колхозных рынках города характеризуется следующими данными:
Таблица 6.1
| Наименование товара |
Продано товаров за период, тыс. кг |
Средняя цена за 1 кг за период, руб. |
| базисный |
отчетный |
базисный |
отчетный |
Колхозный рынок № 1:
Картофель
Свежая капуста
|
6,0
2,5
|
6,2
2,4
|
8,0
15,0
|
8,5
19,0
|
Колхозный рынок №2:
Картофель
|
12,0 |
12,8 |
7,5 |
8,0 |
На основании имеющихся данных вычислите:
1. Для колхозного рынка № 1 (по двум видам товаров вместе):
а) общий индекс товарооборота в фактических ценах;
б) общий индекс цен;
в) общий индекс физического объема товарооборота.
Определите в отчетном периоде прирост товарооборота в абсолютной сумме и разложите по факторам (за счет изменения цен и объема продаж товаров).
Покажите взаимосвязь начисленных индексов.
2. Для двух колхозных рынков вместе (по картофелю):
а) индекс цен переменного состава;
б) индекс цен постоянного состава;
в) индекс влияния изменения структуры объема продажи картофеля на динамику средней цены.
Решение:
1. Для колхозного рынка № 1 определим индивидуальные индексы:
По товару Картофель: i
p = 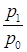 = = 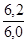 = 1,033 или 103,3%, = 1,033 или 103,3%,
i
q = 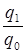 = = 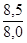 = 1,063 или 106,3%, = 1,063 или 106,3%,
По товару Свежая капуста: i
p = 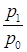 = = 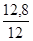 = 0,960 или 96%, = 0,960 или 96%,
i
q = 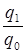 = = 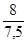 = 1,267 или 126,7%. = 1,267 или 126,7%.
Таблица 6.2
Индивидуальные индексы для товаров колхозного рынка №1
| Индивидуальные индексы |
Продано товаров за период, тыс. кг |
Средняя цена за 1 кг за период, руб. |
| Картофель |
1,033 |
1,063 |
| Свежая капуста |
0,960 |
1,267 |
Таким образом:
– цены на картофель выросли в отчетном году на 6,3%;
– объем продаж по картофелю увеличился на 3,3%.
– цены на свежую капусту выросли в отчетном периоде на 26,7%;
– свежей капусты было продано в отчетном периоде по сравнению с базисным на 4% меньше.
а) Чтобы определить изменение товарооборота в фактических ценах в абсолютной сумме, необходимо рассчитать агрегатный индекс товарооборота в фактических ценах:
I
pq = 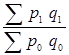 = = 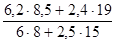 = = 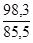 = 1,150 или 115,0%. = 1,150 или 115,0%.
Разность между числителем и знаменателем индекса товарооборота в фактических ценах дает прирост (или снижение) товарооборота в абсолютной сумме:
Δpq = 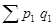 – –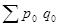 = 98,3-85,5 = 12,8 (тыс. руб.). = 98,3-85,5 = 12,8 (тыс. руб.).
Товарооборот в фактических ценах вырос в отчетном периоде по сравнению с базисным периодом на 15% или на 12,8 тыс.руб.
б) Перейдем к расчету агрегатного индекса цен. В качестве веса введем в индекс неизменное количество товаров отчетного периода (по формуле Пааше). Формула агрегатного индекса цен будет выглядеть следующим образом:
I
p = 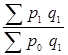 = = 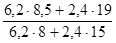 = = 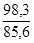 = 1,148 или 114,8%. = 1,148 или 114,8%.
Разность между числителем и знаменателем индекса цен дает прирост (снижение) товарооборота за счет изменения цен:
Δpq(p)
= 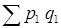 – –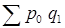 = 98,3-85,6 =12,7 (тыс. руб.). = 98,3-85,6 =12,7 (тыс. руб.).
Прирост товарооборота в абсолютной сумме в отчетном периоде составил 12,7 тыс. рублей за счет увеличения цен на 14,8%.
в) Чтобы рассчитать агрегатный индекс физического объема товарооборота, который будет характеризовать изменение объема продажи товаров, примем в качестве веса неизменные цены базисного периода и определим стоимость каждого товара:
I
q = 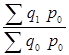 = = 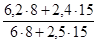 = = 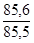 = 1,001 или 100,1%, = 1,001 или 100,1%,
Разность между числителем и знаменателем индекса физического объема товарооборота дает прирост (или снижение) товарооборота в неизменных ценах:
Δpq(q)
= 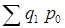 – –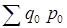 = 85,6-85,5 = 0,1 (тыс. руб.). = 85,6-85,5 = 0,1 (тыс. руб.).
Прирост товарооборота в абсолютной сумме в отчетном периоде за счет увеличения количества проданного товара на 0,1% составил 0,1 тыс. руб.
Связь между изменениями объема товарооборота, количеством продажи товаров и уровнем их цен выражается в системе взаимосвязанных индексов:
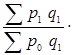 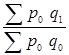 = =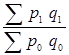 или или 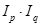 = I
pq , = I
pq ,
тогда в нашем примере:
1,148*1,001=1,150
Произведение двух индексов (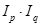 ) дает нам показатель динамики товарооборота в фактических ценах (Ipq), то есть за счет роста цен на 14,8% (в абсолютной сумме – 12,7 тыс.руб.) и увеличения объема продаж на 0,1% (в абсолютной сумме – 100 руб.), товарооборот увеличился в отчетном году на 15% (в абсолютной сумме – 12,8 тыс.руб.). ) дает нам показатель динамики товарооборота в фактических ценах (Ipq), то есть за счет роста цен на 14,8% (в абсолютной сумме – 12,7 тыс.руб.) и увеличения объема продаж на 0,1% (в абсолютной сумме – 100 руб.), товарооборот увеличился в отчетном году на 15% (в абсолютной сумме – 12,8 тыс.руб.).
2. а) Индекс цен переменного состава определим по следующей формуле:
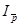 = =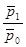 = =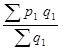 : :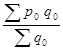
или 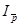 = = : :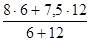 = =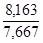 =1,0648 или 106,48%. =1,0648 или 106,48%.
Средняя цена единицы продукции по двум заводам возросла на 6,48%.
б) Индекс постоянного состава определим по агрегатному индексу цен:
I
p = 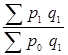 = = 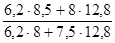 = = 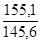 = 1,0652 или 106,52%. = 1,0652 или 106,52%.
Это означает, что в среднем по двум заводам цена единицы повысилась на 6,52%.
в) Индекс структурных сдвигов определим по формуле:
I
стр
= 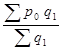 : :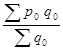
илиI
стр
= 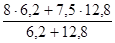 : :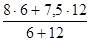 = =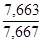 =0,9995 или 99,95% =0,9995 или 99,95%
Средняя цена единицы по двум заводам снизилась на 0,05% за счет изменения удельного веса на отдельном заводе в общем выпуске продукции.
Покажем взаимосвязь трех исчисленных индексов:
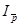 = =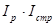 или 1,0652 = или 1,0652 = 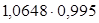 . .
Общий вывод:
Если бы происшедшие изменения цен продукции не сопровождались перераспределениями в ее выпуске, то средняя себестоимость продукции по двум заводам выросла бы на 6,48%.
Изменение структуры выпуска продукции в общем объеме вызвало снижение цен на 0,05%. Одновременное воздействие двух факторов увеличило среднюю цену продукции по двум заводам на 6,52%.
группировка средний прирост дисперсия
Задача № 7
По заводу имеются следующие данные о выпуске продукции:
Таблица 7.1
| Вид продукции |
Выпуск продукции в I квартале, тыс. руб. |
Увеличение (+) или уменьшение (-) выпуска продукции во II квартале по сравнению с I кварталом, % |
| Рельсы трамвайные |
22300 |
+3,0 |
| Чугун литейный |
15800 |
-2,0 |
| Железо листовое |
10500 |
+1,5 |
1.Определить общий индекс физического объема продукции.
2.Определить сумму изменения затрат за счет объема произведенной продукции.
Решение:
1. Определим индивидуальные индексы физического объема товарооборота в таблице:
Таблица 7.2
| Вид продукции |
Выпуск продукции в I квартале, тыс. руб. |
Индивидуальный индекс физического объема, т/об |
| Рельсы трамвайные |
22300 |
1,03 |
| Чугун литейный |
15800 |
0,98 |
| Железо листовое |
10500 |
1,015 |
q = 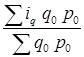 = = 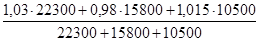 = = 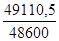 = 1,011 = 1,011
Физический объем продукции увеличился на 1,1%.
2. Сумма изменения затрат равна 49110,5-48600 = 510,5 тыс.руб.
Таким образом за счет увеличения физического объема продукции на 1,1% сумма затрат увеличилась на 510,5 тыс.руб.
Задача № 8
Для изучения тесноты связи между объемом произведенной продукции (факторный признак – Х) и балансовой прибылью (результативный признак – У) по данным задачи № 1 вычислите эмпирическое корреляционное отношение.
Сделайте выводы.
Решение:
Для расчета межгрупповой дисперсии строим расчетную таблицу 8.1.
Таблица 8.1
Расчет среднего квадратического отклонения
| Группы банков по объему произведенной продукции |
Число банков
n
|
Сумма прибыли на один банк, млн.руб. У |
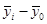 |
(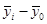 )2 )2 |
(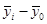 )2n )2n |
| 305-404 |
4 |
15,00 |
-22,520 |
507,150 |
2028,602 |
| 405-503 |
5 |
28,00 |
-9,520 |
90,630 |
453,152 |
| 504-602 |
6 |
36,67 |
-0,853 |
0,728 |
4,369 |
| 603-701 |
5 |
45,60 |
8,080 |
65,286 |
326,432 |
| 702-800 |
5 |
58,00 |
20,480 |
419,430 |
2097,152 |
| Итого: |
25 |
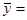 37,52 37,52 |
4909,707 |
Рассчитаем межгрупповую дисперсию по формуле
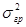 = = 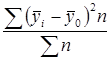 = =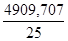 =196,388 =196,388
Для расчета общей дисперсии возведем все значения «у
» (валовую прибыль) в квадрат.
Таблица 8.2
Валовая прибыль, млн.руб.
У
|
Валовая прибыль, млн.руб.
У2
|
Валовая прибыль, млн.руб.
У
|
Валовая прибыль, млн.руб.
У2
|
Валовая прибыль, млн.руб.
У
|
Валовая прибыль, млн.руб.
У2
|
| 45 |
2025 |
59 |
3481 |
41 |
1681 |
| 11 |
121 |
28 |
784 |
36 |
1296 |
| 33 |
1089 |
43 |
1849 |
12 |
144 |
| 27 |
729 |
23 |
529 |
50 |
2500 |
| 55 |
3025 |
35 |
1225 |
29 |
841 |
| 64 |
4096 |
54 |
2916 |
38 |
1444 |
| 14 |
196 |
26 |
676 |
49 |
2401 |
| 37 |
1369 |
58 |
3364 |
ИТОГО
|
40362
|
| 41 |
1681 |
30 |
900 |
Рассчитаем общую дисперсию по формуле:
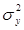 = = 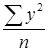 – – 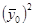 = = 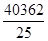 – 37,522 = 206,73 – 37,522 = 206,73
Тогда коэффициент детерминации будет:
η2 =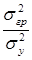 = = 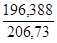 = 0,950. = 0,950.
Он означает, что вариация суммы выданных банком кредитов на 95% объясняется вариацией размера процентной ставки и на 5% – прочими факторами.
|