|
Кинематический и силовой расчет многозвенного зубчатого механизма
Исходные данные.

Рис. 1


Частота вращения ведущего звена nвщ
= 1000 об/мин.
Момент сопротивления на ведомом валу Мс
= 50 Н∙м
Произвести кинематический и силовой расчет многозвенного зубчатого механизма.
1.
Определение неизвестного числа зубьев и количества сателлитов
Ведущее звено – зубчатое колесо 1, ведомое – колесо 3, неподвижное – колесо 6. К колесу 3 приложен момент сопротивления Мс
= 50 Н∙м. Частота вращения ведущего колеса: nвщ
= 1000 об/мин.
Определим недостающее число зубьев колеса Z6
.
Z3
+ Z4
= Z6
– Z5
;
Z6
= Z3
+ Z4
+ Z5
= 28 + 24 + 30 = 82
Выберем число сателлитов:
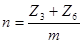 , ,
где m – целое число.
Примем n = 5, тогда 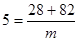 , , 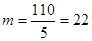
m – целое число, поэтому условие сборки выполняется. Проверим условие соседства.
Для колес 3 и 4:
(Z3
+ Z4
)·sin (180°/n) > Z4
+ 2
(28 + 24)·sin (180°/5) > 24 + 2
30,6 > 26
Для колес 5 и 6:
(Z6
– Z5
)·sin (180°/n) > Z5
+ 2
(82 – 30)·sin (180°/5) > 30 + 2
30,6 > 32 – неверно. Условие соседства не выполняется.
Примем n = 2, тогда  , , 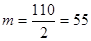
m – целое число, поэтому условие сборки выполняется. Проверим условие соседства.
Для колес 3 и 4:
(28 + 24)·sin (180°/2) > 24 + 2
52 > 26
Для колес 5 и 6:
(82 – 30)·sin (180°/2) > 30 + 2
52 > 32 – верно.
Условие соседства выполняется.
2.
Определение передаточного отношения
Определим передаточное отношение аналитическим способом. Рассматриваемый механизм состоит из комбинации одной ступени колес с неподвижными осями (1 – 2) и планетарной ступени (5 – 6 – 4 – 3). Общее передаточное отношение равно:
Uобщ
= U13
= U12
· UН3
(6)
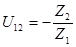


Передаточное отношение меньше единицы, поэтому механизм является мультипликатором. Uобщ
< 0, следовательно, ведущее и ведомое колеса вращаются в разные стороны.
3.
Определение радиусов окружностей колес
Вычислим радиусы начальных окружностей всех колес, которые по принятому условию, совпадают с делительными окружностями:
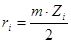 ; ;
 ; ;
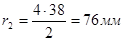 ; ;
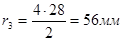 ; ;
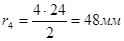 ; ;
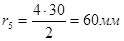 ; ;
 . .
Вычертим в масштабе кинематическую схему механизма.
Определим степень подвижности механизма.
Степень подвижности механизма W определяется по формуле Чебышева:
W = 3n – 2p5
– p4
,
где n = 4 – число подвижных звеньев,
p5
= 4 – число кинематических пар V класса (О1
, О2
, О3
, О4
),
p4
= 3 – число кинематических пар IV класса (А, В, С).
Получаем: W = 3·4 – 2·4 – 3 = 1, т.е. механизм имеет одно ведущее звено – зубчатое колесо 1.
4.
Силовой расчет
Так как задан момент сопротивления МС
, силовой расчет начнем с рассмотрения квазистатического равновесия колеса 3. Покажем его схему нагружения.
К колесу 3 приложен момент сопротивления МС
.
Вследствие того, что выбрано два сателлита в точках В, В’ изобразим две силы 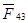 со стороны колеса 4 блока сателлитов 4–5, действующих на колесо 3. Эти силы направлены так, чтобы момент, создаваемый ими, уравновесил момент МС
. со стороны колеса 4 блока сателлитов 4–5, действующих на колесо 3. Эти силы направлены так, чтобы момент, создаваемый ими, уравновесил момент МС
.
Составим два уравнения.
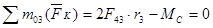 ;
;
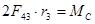 ;
;
 . .
 ; ;
Рассмотрим схему нагружения блока сателлитов 4–5. На блок сателлитов 4–5 действуют силы со стороны колес 3 и 6, а также сила 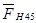 со стороны водила. со стороны водила.
Составим два уравнения.
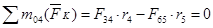 ;
;
 ;
;
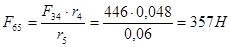 . .
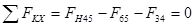 ; ;

Рассмотрим нагружение водила Н и колеса 2. Со стороны блока сателлитов на водило действуют силы  . На колесо 2 со стороны колеса 1 действует сила . На колесо 2 со стороны колеса 1 действует сила  . Со стороны стойки действует сила . Со стороны стойки действует сила  . .
Составим два уравнения.
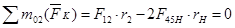 ;
;
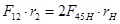 ;
;
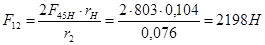 . .
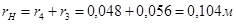
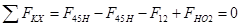 ; ;
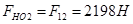
Рассмотрим нагружение колеса 1. Со стороны колеса 2 на него действует сила  . Чтобы уравновесить момент от этой силы, к колесу 1 должен быть приложен момент. Это движущий момент Мд
. Со стороны стойки действует сила . Чтобы уравновесить момент от этой силы, к колесу 1 должен быть приложен момент. Это движущий момент Мд
. Со стороны стойки действует сила 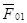 . .
Составим два уравнения.
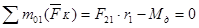 ;
;
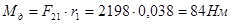 .
.
 ; ;

Проверим правильность проведенных вычислений:
МС
= – Мд
∙ Uобщ
50 = 84 ∙ 0,598
50 ≈ 50,2
В пределах погрешности округлений получили тождество. Расчеты проведены, верно.
5.
Нагружение стойки. Определение тормозного (реактивного) момента
В местах крепления колес с неподвижными осями 1 и 2 на корпус через валы колес действуют силы  , , 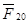 . Кроме того, стойкой является и неподвижное колесо 6, закрепленное на корпусе. На это колесо со стороны колеса 5 действуют силы . Кроме того, стойкой является и неподвижное колесо 6, закрепленное на корпусе. На это колесо со стороны колеса 5 действуют силы 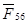 , которые также будем обозначать , которые также будем обозначать 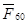 . .
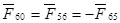
Этих сил две, так как механизм имеет два блока сателлитов. Покажем схему нагружения стойки.
Составим уравнение статики для стойки.
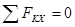 ; ;

357 – 357 + 2198–2198 = 0
0 = 0
Следовательно, равнодействующая реактивных сил, приложенных к стойке, равна нулю.
Тормозной (реактивный) момент найдем из уравнения моментов.

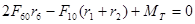
2·357·0,164 – 2198·(0,038 + 0,076) + МТ
= 0
МТ
= 134 Н·м
Проверим выполнение равенства:
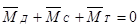 . .
С учетом направлений моментов получим:
134 – 50 – 84 = 0
0 = 0 – верно.
6.
Определение мощности на ведущем и ведомом валах
Мощность на ведущем валу:
N1
= Mд
· щвщ
;
 . .
N1
= 84 · 104,7 = 8795 Вт = 8,795 кВт
Мощность на ведомом валу:
N3
= MС
· щвм
;
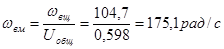 . .
N3
= 50 · 175,1 = 8755 Вт = 8,755 кВт
Так как к.п.д. не задан, мощность на ведущем валу:
N1
’ = N3
= 8,755 кВт
Погрешность округлений:
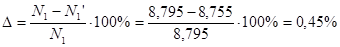
7. Построение эвольвентного зацепления зубчатых колес
сателлит колесо нагружение тормозной вал
Построим эвольвентное зацепление зубчатых колес 1 и 2. Отложим на чертеже в масштабе межцентровое расстояние зубчатых колес 1 и 2. Получим точки О1
и О2
. Из этих точек проводим основные окружности радиусами Rb
1
и Rb
2
. Из точки пересечения окружности радиусом Rb
1
и вертикальной оси проводим горизонтальную линию. Эту точку обозначим за 0. Разобьем, полученную линию на отрезки длиной 20 мм, начиная от точки 0. Получим точки 1, 2, 3, 4, 5. Размер эвольвенты определяет необходимое количество точек. Из точки 0 проводим окружности радиусами: 01, 02, 03, 04, 05. Находим точки пересечения этих окружностей с окружностью Rb
1
. Получаем точки: 1’, 2’, 3’, 4’, 5’. Через эти точки проводим касательные к окружности Rb
1
.
Из точек: 1’, 2’, 3’, 4’, 5’ проводим окружности радиусами: 1’0, 2’0, 3’0, 4’0, 5’0. Точки пересечения этих окружностей с соответствующей касательной будут определять точки искомой эвольвенты.
Проводим окружность, определяющую вершины зубьев, радиусом Rа1
. По полученным точкам проводим эвольвенту до пересечения с окружностью вершин. Чертим окружность, определяющую делительный диаметр (Rw
1
) и окружность впадин (Rf
1
).
По делительному диаметру откладываем толщину зуба. Вторую часть зуба чертим зеркально первой относительно середины линии, определяющей ширину зуба.
Соединяем центр окружности О1
с серединой линии, определяющей ширину зуба. Проводим два отрезка параллельно полученной линии от начала эвольвент до пересечения с окружностью впадин.
Для построения других зубьев необходимо отложить шаг зацепления по делительной окружности и повернуть относительно центра О1
, имеющийся зуб на этот шаг. После вычерчивания необходимого числа зубьев делаются галтели.
Зубья второго колеса строятся аналогично. Чтобы зубья обеих колес находились в зацеплении необходимо зубья одного колеса повернуть до соприкосновения с зубьями другого.
Для определения угла перекрытия проводим радиусы начальных окружностей, которые в нашем случае совпадают с делительными. Пересечение начальных окружностей дает полюсную точку Р. Проведем через эту точку касательные к основным окружностям. Точки пересечения окружностей вершин зубьев и этой касательной определяют длину линии зацепления.
Список литературы
1. Артоболевский И.И. Теория механизмов и машин. М., 1988 г.
2. Девятова Е.М., Кичин И.Н., Сафронов А.А. Методические указания по курсу ТММ: Анализ и синтез зубчатого механизма А10–137. М.: Изд-во МГИУ, 1990 г.
3. Кичин И.Н. Методические указания к выполнению курсового проекта по теории механизмов и машин. М., 1987 г.
|