Контрольная работа: Алгоритмы сбора и предварительной обработки измерительной информации

Содержание

Введение

1. Типовые алгоритмы сбора измерительной информации

2. Введение поправок

3. Сглаживание исходных данных

Выводы

Литература

Введение

Тема контрольной работы "Алгоритмы сбора и предварительной обработки измерительной информации" по дисциплине "Измерительные информационные системы (ИИС)".

Программно-математическое обеспечение ИИС является не менее важным ее компонентом, чем аппаратные средства. Алгоритмы сбора и обработки информации в значительной степени определяются характером решаемых задач, и этому вопросу будут посвящены следующие главы. Однако имеется ряд алгоритмов, которые могут быть общими для различных ИИС.

1. Типовые алгоритмы сбора измерительной информации

Неотъемлемым компонентом алгоритмов сбора первичной измерительной информации является ее дискретизация.

С дискретизацией мы сталкиваемся при сборе исходной информации и при ее обработке. На определенной стадии развития ИИС дискретизация на обоих этапах приводила к погрешностям результатов измерения. При ограниченности средств вычислительной техники того периода погрешность вычисления была сопоставима с аппаратными и методическими погрешностями. Однако возможности современных ЭВМ таковы, что вызываемая ими в процессе дискретизации погрешность не имеет практического значения. Разрядность чисел в ЭВМ всегда намного превышает разрядность вводимой информации. Вычисление, например, интегралов от аналитически заданных функций сводится к вычислениям сумм от дискретных значений этих функций. При этом всегда может быть обеспечена требуемая точность вычислений. Существенно большее влияние имеет дискретизация, связанная с алгоритмом сбора исходной информации и обусловленная характером ИО.

Физические величины, коды которых выдаются измерительным каналом, неизбежно подвергаются дискретизации по уровню. В силу конечности числа разрядов АЦП (п) дискретность воспринимаемой каналом физической величины х равна

(1)

где X — диапазон возможных изменений величины х.

Характеристика АЦП при правильном округлении приведена на рис. 1.

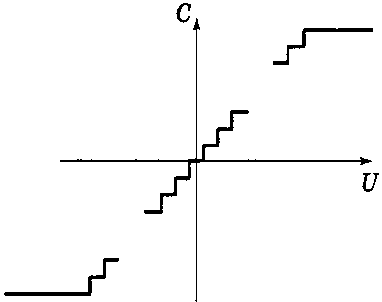
Рис. 1

При округлении в меньшую сторону (отбрасывается вся часть неполной дискреты) характеристика смещается на bх/2 вправо, при округлении в большую сторону — на ту же величину влево.

Дискретизация по уровню приводит к погрешности, имеющей равномерное распределение на интервале длиной bх. Среднее квадратичное отклонение этой погрешности а = = bх/2 √3 , а математическое ожидание равно нулю при правильном округлении в АЦП, равно -bх/2 при округлении в меньшую сторону и bх/2 при округлении в большую сторону. Из сказанного следует, что мы имеем довольно простое универсальное описание погрешностей дискретизации по уровню.

Важной особенностью погрешности дискретизации является независимость ее значений для разных результатов. Это свойство широко используется при моделировании случайных равномерно распределенных чисел. В силу этого свойства при усреднении и других алгоритмах обработки, приводящих к сжатию результатов, влияние этой погрешности существенно уменьшается, и распределение погрешности результата обработки можно считать близким к нормальному.

При малом числе разрядов АЦП погрешность дискретизации может иметь существенное значение, и ее необходимо учитывать при оценке достоверности получаемых результатов. Разрядность АЦП в ИК меньше, чем разрядность чисел в ЭВМ. Тем не менее всегда можно выбрать такую разрядность серийно выпускаемого АЦП, при которой погрешность дискретизации по уровню будет пренебрежимо мала.

Более существенное влияние имеет дискретизация значений аргумента (аргументов) при исследовании функций. Наиболее часто исследуются функции времени, когда несколько или все физические величины, связанные с ИО, зависят от времени. Однако аргументами могут быть пространственные координаты и любые другие физические величины. В этом случае мы сталкиваемся с серьезной методической проблемой — невозможностью измерения функции как единого целого. Мы можем измерить конечное число значений функций для некоторого набора значений аргумента (аргументов). Как правило, соседние значения аргументов отстоят друг от друга на равные интервалы — равномерный шаг дискретизации (квантования) по аргументу. Однако иногда используется и неравномерный шаг дискретизации.

Остановимся на дискретизации по времени.

В этом случае ИК выдают значения исследуемой физической величины x_j взятые в моменты времени t_j . Естественно, эти отсчеты, представляемые в цифровом виде, квантованы по уровню и в зависимости от скорости изменения исследуемой величины соседние отсчеты могут отличаться друг от друга на несколько дискрет. Из этого следует, что погрешность восстановления функции по ее дискретным отчетам может быть весьма значительной, и она зависит не только от интервалов времени между соседними отсчетами, но и от скорости изменения исследуемой физической величины. В этом случае мы не располагаем столь же простым описанием погрешности дискретизации, которое имеется при дискретизации по уровню. Следует отметить, что задача восстановления функции по ее отсчетам не является обязательной при исследовании функции. Как мы увидим в следующей главе, интересующие нас величины в большинстве случаев могут определяться непосредственно по дискретным отсчетам. Однако анализ погрешностей определения этих величин будет специфичным для каждой конкретной задачи и потребует определенной априорной информации об исследуемой функции.

Рассматривая дискретизацию величины по уровню, мы отмечали, что практически всегда число этих уровней велико, и они близко отстоят друг от друга. При дискретизации по времени моменты отсчетов достаточно далеко отстоят друг от друга. При этом следует иметь в виду, что t_j также дискретизированы по уровню. Шаг дискретизации по времени может быть сделан достаточно малым, и он всегда много меньше интервалов времени между соседними отсчетами. Однако эту дискретизацию также следует учитывать. Причем она может оказаться более значительной, если аргументом является не время, а некоторая другая величина.

Погрешность из-за дискретизации аргументов будет тем меньше, чем чаще берутся отсчеты. Очевидными физическими ограничениями частоты отсчетов являются время преобразования АЦП, пропускная способность каналов связи и быстродействие ЭВМ. Эти факторы необходимо учитывать, но не они являются определяющими. Существенно больше влияют инерционность ИО и инерционность ИК, обусловленная инерционностью измерительных преобразователей, как первичных, так и вторичных.

Если объект достаточно инерционен и, следовательно, функции x_i (t) достаточно медленные (достаточно низкочастотные), увеличение частоты отсчетов не повысит существенно информативность первичных данных. Можно повысить достоверность этих данных за счет их усреднения, но это повышение также не беспредельно. Этот фактор, не зависящий от свойств ИИС, ограничивает сверху реально необходимую частоту отсчетов.

Точно так же нецелесообразно брать отсчеты с периодом существенно меньшим, чем постоянная времени (время памяти) измерительных преобразователей. Однако эта ситуация принципиально отличается от предыдущей и означает, что задачи выбора частоты дискретизации и обеспечение требуемого быстродействия ИК должны решаться совместно. Медленность исследуемых функций является отражением реальных свойств ИО, а их искажения за счет инерционности ИК и обусловленной этим низкой частотой отсчетов приводит к увеличению аппаратных погрешностей. Поэтому быстродействие ИК должно быть согласовано с возможной скоростью изменения измеряемых величин, и только после этого может выбираться рациональная частота отсчетов.

Соседние отсчеты функции могут существенно отличаться друг от друга, однако их разность по абсолютной величине в среднем меньше абсолютных значений самих отсчетов. Это обстоятельство используется для сжатия данных при их передаче по цифровым каналам связи (разностная модуляция). В этом случае первый отсчет передается полностью, а в последующие моменты передаются разности x_j – x_{j -1} .Очевидно, что такая передача информации менее помехоустойчива, чем передача отсчетов функции, поскольку сбой при передаче одной разности не устраняется при передаче следующих значений. Однако в силу достаточно высокой помехоустойчивости цифровых каналов связи за счет использования помехоустойчивых кодов эта погрешность оказывается достаточно малой. При разностной модуляции значения t_j могут быть как равномерными, так и неравномерными.

Разновидностью разностной модуляции является дельта-модуляция, которая в принципе предполагает неравномерность моментов отсчетов. Сущность дельта-модуляции состоит в том, что по каналу связи передается один бит информации в момент времени, когда измеряемая величина изменилась по уровню на одну дискрету. Передаваемый бит содержит информации о знаке изменения (рис. 2).

В этом случае отсчеты будут следовать тем чаще, чем больше скорость изменения измеряемой величины. С этой точки зрения дельта-модуляцию можно рассматривать как адаптивную процедуру сбора и передачи данных. При этом разность между дискретным и непрерывным представлениями функции не будет превышать одной дискреты.

Очевидно, что передача данных со сжатием информации требует наличия в ИК вычислительных устройств, определяющих разности и вырабатывающих командные сигналы для передачи данных. Более подробные сведения о разностной модуляции, дельта-модуляции и других способах сжатия данных при их передаче можно найти в [29].

Самый простой алгоритм сбора информации об изменяющихся во времени величинах — считывание по команде с ЭВМ или извне отсчетов со всех ИК. Такой алгоритм применим как для периодических, так и для непериодических отсчетов. Исключение составляет передача информации дельта-модулированным сигналом, когда время отсчета определяется передающим устройством. Если функции x_i (t) исследуются независимо друг от друга, то синхронность отсчетов всех функций не важна. Если же эти функции рассматриваются как единое целое, то моменты времени отсчетов должны быть согласованы. При этом может возникнуть необходимость введения поправок, если отсчеты взяты в разные моменты времени. Причиной неодновременности отсчетов может быть конечное время преобразования в АЦП при его работе в мультиплексном режиме, задержки в каналах связи и др.

Теперь остановимся на процедуре сбора первичной информации, когда одна или несколько исследуемых физических величин рассматриваются как функции одной или нескольких других физических величин. Это не всегда означает, что измеряемые физические величины оказались разбиты на два вида: зависимые, присущие непосредственно ИО, и независимые, внешние факторы, влияющие на свойства этого объекта. Например, при исследовании формы поверхностей деталей любая из пространственных координат может рассматриваться как функция двух других координат. Однако все три координаты одинаково описывают свойства исследуемой детали.

При исследовании зависимости сопротивления резистора от температуры сопротивление действительно является свойством ИО, а температура — внешним влияющим фактором. Однако и в этом случае с точки зрения сбора и обработки первичной информации обе физические величины ничем не отличаются. Необходимо измерять температуру самого резистора, а не нагревателя и не окружающей среды. Более того, нагрев можно производить, пропуская через резистор достаточно большой ток, и измерять величину этого тока, падение напряжения на резисторе и его температуру. При этом также следует иметь в виду, что полученная функция зависимости сопротивления от температуры описывает свойства ИО, то есть присуща именно ему.

Из приведенных примеров можно сделать вывод, что при исследовании функциональных зависимостей между измеряемыми физическими величинами их разбиение на аргументы и функции довольно условно, хотя в отдельных случаях измеряемые величины можно разбить на присущие непосредственно объекту и на внешние влияющие факторы. Однако по отношению к алгоритмам сбора и обработки первичной информации это разбиение несущественно.

Для исследования функциональных зависимостей необходима достаточно большая совокупность отсчетов измеряемых физических величин. Желательно, чтобы она охватывала всю область возможных значений величин при реальной эксплуатации объекта. Для сбора этой информации могут использоваться пассивный и активный методы.

При пассивном методе по команде с ЭВМ считываются значения всех физических величин ИО. Естественно, при этом мы получаем только по одному значению каждой величины, чего недостаточно для изучения функций. Получить большее число значений можно либо исследуя однотипные объекты, либо предполагая, что исследуемые величины изменяются во времени, и произведя несколько считываний в разные моменты времени. Пассивный метод мало эффективен и используется только в тех случаях, когда активный метод, предусматривающий воздействие на ИО, физически невозможен. Пассивный метод относительно эффективен при исследовании зависимости физических величин от пространственных координат при использовании так называемых многоточечных систем, когда исследуемые величины измеряются в разных точках пространства. В этом случае для получения достаточно большего объема данных необходимо иметь большое количество однотипных ИК.

При активном методе значения величин, рассматриваемых как аргументы, изменяются путем внешних воздействий на ИО. При исследовании величин, зависящих от пространственных координат, активное воздействие предполагает перемещение первичного преобразователя относительно объекта по одной, двум или трем координатам. При этом, естественно, предполагается, что свойства ИО не изменяются во времени. В зависимости от формы ИО система координат, в которой производится сбор первичной информации и, соответственно, перемещение датчика, может быть декартовой, полярной, цилиндрической или сферической. Обычно одна координата изменяется непрерывно, а другие (одна или две) изменяются дискретно с достаточно большим шагом. Значения непрерывно изменяемой координаты и функции считываются через заданные интервалы перемещения по этой координате или через заданные интервалы времени. Время в этом случае не является аргументом для какой-либо физической величины, а служит вспомогательной переменной. Очевидно, что в этом случае базирующее устройство должно иметь привод, обеспечивающий необходимые перемещения. Такое непрерывное изменение одной из координат в процессе сбора информации иногда называют сканированием. Более часто сканирование используется при бесконтактных методах, восходя к исходному пониманию этого термина в радиолокации.

Технически самой сложной будет ситуация, когда аргументы исследуемых величин не являются ни временем, ни пространственными координатами. В этом случае базирующее устройство должно содержать преобразователи, формирующие по командам с ЭВМ соответствующие воздействия с заданными значениями. Некоторые воздействия, например магнитные или электрические поля, могут изменяться практически мгновенно. В этом случае, как и при изменении пространственных координат, аргументы могут изменяться дискретно или непрерывно. Во втором случае значения аргументов и функций могут считываться с заданным шагом по аргументу или времени. Некоторые аргументы, например температура, влажность, химический состав, требуют для достижения заданного значения определенного времени. В этом случае алгоритм сбора данных может предусматривать непрерывное измерение изменяющегося аргумента в пределах интересующего интервала значений. Изменение необязательно должно быть равномерным во времени, поскольку значения аргумента и значения функции могут фиксироваться с заданным шагом аргумента. Рассмотренные выше алгоритмы сбора первичной информации, за исключением дельта-модуляции, предполагают периодическую выдачу отсчетов измеряемой физической величины. Однако любая регулярная система отсчетов может привести для определенных функций к систематическим погрешностям. Это можно проиллюстрировать простейшим примером. Пусть исследуемая функция — периодическая, целью измерения является определение ее постоянной составляющей а₀ , а отсчеты берутся с периодом Т₀ , кратным периоду исследуемого сигнала (рис. 3).

Тогда в зависимости от фазового сдвига между исследуемым сигналом и последовательностью отсчетов систематическая погрешность измерения постоянной составляющей будет лежать в пределах ±А независимо от числа усредняемых отсчетов. Устранить эту систематическую (при фиксированных временных соотношениях) погрешность можно, беря отсчеты в случайные моменты времени t_j = jT₀ + τ_j , где τ_j — независимые случайные величины, равномерно распределенные на интервале [0; Т₀ ]. При этом возникает случайная погрешность, уменьшающаяся с увеличением числа отсчетов. Такая процедура устранения влияния систематических факторов путем искусственного введения случайности в процесс исследования называется рандомизацией. Примеры таких задач можно привести из самых различных областей. В свое время, когда разрядность АЦП не превышала восьми, усредняя несколько последовательных результатов преобразования, путем рандомизации искусственно увеличивали разрядность отсчетов.

В теоретическом плане анализ погрешностей из-за дискретизации функции нескольких аргументов аналогичен анализу погрешностей из-за дискретизации по времени. В общем случае оценить качество дискретизации и принять решение о ее приемлемости можно, рассматривая оценки достоверности решаемых задач для разных методов дискретизации. При этом теоретически или путем моделирования можно сравнивать реализуемые способы дискретизации с идеальными, практически нереализуемыми.

2. Введение поправок

Наиболее простой и распространенный случай — введение поправок на известную систематическую погрешность ИК. Аналогичные поправки могут вводиться во всех видах СИ. Алгоритм введения поправки очевиден: из кода, выдаваемого ИК, должен вычитаться код известной систематической погрешности. Поправка на аддитивную систематическую погрешность задается в виде одного числа, а поправка на мультипликативную систематическую погрешность предварительно рассчитывается в соответствии с заложенным алгоритмом с учетом результата измерения соответствующего ИК. Например, поправка на систематическую погрешность коэффициента передачи измерительного канала равна результату измерения, умноженному на относительную систематическую погрешность коэффициента передачи, оцененную экспериментально.

Специфичными для ИИС являются поправки на систематические погрешности, обусловленные взаимным влиянием каналов. Для ИК погрешность, вызванная влиянием другого канала, может быть как аддитивной (например, из-за проникновения сигнала по паразитным каналам связи), так и мультипликативной (например, из-за изменения нагрузки на общий источник питания ПИП или ВИП). Однако рассчитываются эти поправки аналогично поправкам на собственные мультипликативные погрешности в соответствии с алгоритмом, описывающим взаимное влияние каналов, с учетом данных о сигнале в канале, влияние которого компенсируется.

Поправки на систематическую погрешность для каждого отсчета, выдаваемого ИК, являются числами. Однако для разных отсчетов они могут рассматриваться как функции времени или других аргументов. В частности, как следует из определения систематической погрешности [33], она остается постоянной или закономерно изменяется. Если закон изменения известен, то вводимая поправка оказывается переменной. К поправкам в виде функций мы приходим при компенсации взаимного влияния каналов и в некоторых других случаях, например при компенсации влияния внешних факторов.

Как и для других СИ, величины поправок и алгоритмы их расчета определяются на основе теоретических и экспериментальных исследований метрологических характеристик ИК. Например, при питании вторичных преобразователей в виде мостов переменного тока от одного генератора систематическая погрешность будет пропорциональна величине сигнала во влияющем канале. К этому выводу можно прийти из анализа мостовой схемы с учетом внутреннего сопротивления питающего генератора. Величину коэффициента пропорциональности для каждого канала проще определить экспериментально, поскольку применение теоретических методов все равно потребует некоторых числовых данных, которые можно получить только экспериментально. К вопросу о введении поправок мы вернемся при анализе погрешностей измерения.

Более сложным является введение поправок, компенсирующих дополнительную погрешность, вызванную внешними условиями. Наиболее часто вводятся температурные поправки, в частности при линейных измерениях. Величина поправки, вычитаемая из результата измерения, в этом случае рассчитывается по формуле

(2)

где L_изм — результат измерения; t ° и

а_и — температура и коэффициент температурного расширения измерительной оснастки, контактирующей с измеряемой деталью;

t° и а_д — то же для измеряемой детали.

Для определения поправки необходимо измерить температуры детали и измерительной оснастки, то есть ввести в ИИС два новых ИК. Аналогичные поправки могут вводиться и для компенсации изменения сопротивления резисторов. При этом в зависимости от материала резистора может использоваться линейная или экспоненциальная модель зависимости сопротивления от температуры.

Напряжение, питающее мосты или делители, определяет их чувствительность. Поэтому дополнительный ИК, измеряющий это напряжение, дает возможность автоматически вводить поправку на нестабильность чувствительности ИК, обусловленную нестабильностью питающего напряжения.

Аналогично могут компенсироваться влияния давления, влажности, изменения питания (не обязательно электрического), электрических и магнитных полей и многих других физических факторов. Для измерения влияющих факторов должны использоваться специальные ИК, что не является спецификой ИИС, поскольку при использовании неавтоматизированных СИ поправки определялись с учетом результатов измерения влияющих факторов с помощью других СИ. Алгоритмы введения этих поправок индивидуальны в каждом конкретном случае и определяются в ходе специальных исследований.

Если исследуемые физические величины рассматриваются как единое целое, необходимо одновременное получение их отсчетов. Однако из-за временных сдвигов в ИК отсчеты этих величин x_ji могут браться в различные моменты времени t_y . Для привязки их к одинаковым моментам времени t_ji можно использовать линейную интерполяцию наблюдаемых функций

(3)

Два последовательных отсчета измеряемой величины, входящих в (3), выбираются таким образом, чтобы t_ji < t_j < t_{j , i +1} .

В принципе для интерполяции в (3) могут использоваться и полиномы более высоких степеней, если отсчеты достаточно разнесены во времени.

Для отдельных областей измерения могут применяться специфичные алгоритмы предварительной обработки, используемые во всех ИИС данной области. Например, при геометрических измерениях измерительный наконечник перемещается по эквидистанте относительно исследуемой поверхности. Эквидистанта — линия (поверхность), все точки которой равноудалены от данной линии (поверхности), то есть они находятся на некоторых нормалях к исследуемой поверхности на равных расстояниях от нее. Эквидистанта к прямой (плоскости) — прямая (плоскость), к окружности (сфере) — окружность (сфера). Во всех остальных случаях форма эквидистанты отлична от формы исходной линии или поверхности.

Поэтому собранный массив данных должен пересчитываться в координаты точек поверхности. Поскольку за счет конечного диаметра измерительного наконечника происходит специфичное сглаживание исследуемой поверхности, полное восстановление исследуемой поверхности не всегда возможно.

При исследовании температуры малых объектов иногда приходится корректировать собранные данные с учетом теплоемкости чувствительного элемента датчика, контактирующего с объектом. При электрических измерениях иногда посредством поправок компенсируется влияние внутреннего сопротивления датчиков. При измерении характеристик радиосигналов на сверхвысоких частотах приходится вводить поправки с учетом коэффициентов отражения. Подобные примеры можно привести для многих областей измерения.

Нелинейность ИК является одним из частных источников систематической мультипликативной погрешности. Поэтому линеаризацию характеристик можно рассматривать как частный случай введения поправок. Однако введение этих поправок базируется на столь специфичном алгоритме, что его рассматривают как самостоятельную процедуру.

Нелинейность любого элемента ИК и всего канала характеризуется максимальным отклонением характеристики от прямой, соединяющей граничные точки рабочего диапазона. Наибольший вклад в нелинейность вносят первичные и вторичные измерительные преобразователи. Однако некоторую нелинейность могут вносить АЦП и каналы связи.

Очевидно, что нелинейность можно устранить, если она стабильна. Только в этом случае вызываемую ею погрешность можно рассматривать как систематическую и компенсировать ее, вводя поправки путем линеаризации. Если вид характеристики преобразования достаточно быстро меняется в процессе эксплуатации ИИС, устранить нелинейность практически невозможно, поскольку вносимая погрешность будет близка к случайной. При медленном изменении формы характеристики, когда ее существенные изменения происходят за недели или месяцы, возможна компенсация ее нестабильности за счет периодического повторения режима линеаризации (настройки).

При аналоговых методах обработки для компенсации нелинейности измерительных преобразователей использовались различные электронные компоненты, работающие на нелинейных участках своих характеристик: лампы, диоды, транзисторы. Таким способом удавалось уменьшить нелинейность в полтора-два раза. Линеаризация проводилась для усредненных характеристик, подстройка для конкретных экземпляров преобразователей была сложна. Поэтому нелинейность измерительных преобразователей являлась основным фактором, ограничивавшим их точность. Ситуация принципиально изменилась с использованием для линеаризации цифровых устройств.

Применяются два основных алгоритма линеаризации:

- аппроксимация характеристики преобразования полиномом (степенным, гармоническим и др.);

- кусочно-линейная аппроксимация.

Оба метода эффективно устраняют нелинейность, если характеристика изменяется достаточно плавно (вторая производная меняет знак в рабочем диапазоне малое число раз). Нелинейность, обусловленная физическими эффектами, заложенными в принцип работы преобразователя, имеет именно такой плавный характер. Неплавная нелинейность обусловлена особенностями конструкции и качеством изготовления. Например, дефекты намотки катушек индуктивных преобразователей приводят к неплавной нелинейности. (Интервал перемещений, в пределах которого происходит изменение знака второй производной, близок к величине шага намотки, то есть составляет несколько сотых долей миллиметра.) Устранить такую нелинейность практически невозможно, поскольку для этого потребуются или полиномы очень высоких степеней, или очень большое число отрезков кусочно-линейной аппроксимации.

Оба метода имеют свои преимущества и недостатки. Однако более широкое применение нашел второй метод, как более простой и более эффективно устраняющий локальную нелинейность.

При первом подходе ищутся параметры функции известной формы (например, степенного полинома), при которых точки (x_j ; C_j ) наименее удалены от этой функции.

Кусочно-линейная аппроксимация (на рис. 4 длина отрезка 1 характеризует нелинейность) заключается в том, что нелинейная характеристика канала заменяется отрезками прямых, проходящих через экспериментально полученные точки (x_i ; C_i ) и (х_{i + 1} ; C_{i + l} ), где i = 1, п. Обычно число точек равно 6... 11, что соответствует аппроксимации пятьюдесятью отрезками прямых.

Координаты узлов аппроксимации должны быть измерены с погрешностями, в несколько раз меньшими допускаемой погрешности ИК, аналогично тому, как это делается при калибровке или поверке.

С учетом вида аппроксимации характеристики преобразования обратное преобразование, обеспечивающее линеаризацию, также будет линейно-кусочной функцией

(4)

Очевидно, что с увеличением числа линейных отрезков обеспечивается более высокая линейность. Однако при этом возрастают требуемый объем памяти (что не очень существенно) и объем экспериментальных работ по получению исходных данных.

Кусочная линеаризация позволяет уменьшить нелинейность в несколько раз и даже в десятки раз. Благодаря этому, используя датчики, конструкция которых не менялась несколько десятилетий, можно обеспечить значительно более высокую точность измерения. При этом подчеркнем, что в соответствии с рассмотренным алгоритмом производится линеаризация характеристики конкретного экземпляра датчика, а не усредненной характеристики, что устраняет и влияние разброса характеристик.

Аппаратно линеаризация может производиться центральной ЭВМ или специальными микропроцессорными устройствами, входящими в состав ИК и конструктивно объединенными с вторичными преобразователями или с АЦП. Некоторые датчики выпускаются в комплекте с ПЗУ, в котором записаны данные о его характеристике, достаточные для линеаризации.

3. Сглаживание исходных данных

На первичную информацию, выдаваемую ИК, могут накладываться локальные возмущения, искажающие характер этой информации. Причин этих локальных возмущений в основном две.

Первой причиной становятся случайные погрешности ИК, которые, как и для любых СИ, определяются только свойствами ИИС.

Второй причиной являются локальные неоднородности ИО, которые не зависят от свойств СИ и не учитываются в рамках используемых физических и математических моделей ИО. Наличие таких возмущений не является принципиально новым. Например, при измерении действующего значения напряжения сети переменного тока с помощью вольтметра на результате измерения сказываются шумы и помехи, накладывающиеся на это напряжение. Однако влияние этих шумов незначительно, поскольку они усредняются за счет инерционности вольтметра. В этом случае быстродействие ИК (в целом положительный фактор) приводит к отрицательным последствиям — фиксации в "мгновенных" отсчетах значений шумов.

Другой пример локальных воздействий, обусловленных свойствами ИО, — локальные флуктуации температуры воздуха за счет турбулентных потоков. К локальным неоднородностям относится шероховатость, имеющая масштабы порядка микрометров и долей микрометров, и волнистость поверхности, имеющая существенно большие масштабы.

Получая с ИК большое количество отсчетов, детально описывающих изменения исследуемой физической величины, можно построить оптимальные алгоритмы обработки этой информации, обеспечивающие наилучшее подавление этих локальных возмущений. Однако объем передаваемой и обрабатываемой информации при этом может оказаться нерационально большим. Для уменьшения этого объема производится сглаживание информации. В результате сглаживания ее объем уменьшается в несколько раз, а иногда и в десятки раз. Сразу отметим, что вводя предварительное сглаживание, мы отказываемся от оптимальной обработки исходной информации. Поэтому используемые субоптимальные алгоритмы обработки сглаженной информации дадут несколько худшие результаты. Это ухудшение обычно оказывается незначительным. Однако при выборе алгоритма сглаживания наличие этого ухудшения нужно иметь в виду и хотя бы ориентировочно оценивать его величину.

Наиболее часто производится сглаживание первичной информации во времени. В этом случае алгоритм обработки, называемый иногда оператором текущего среднего, очень прост:

(5)

Это соотношение записано в дискретной форме. Однако с целью теоретического анализа удобнее записать его для непрерывного времени:

(6)

Соотношение (6) является приближением к (5), поскольку на практике в большинстве случаев обработка ведется в дискретной форме, хотя иногда и используется сглаживание аналоговых сигналов с помощью интегрирующих RС-цепочек, интегрирующих операционных усилителей или других аналоговых фильтров. Алгоритмы (5) и (6) физически реализуемы и могут работать в реальном времени, поскольку для расчета усредненного значения используются значения (отсчеты) сигнала только в предшествующие моменты времени. Однако это приводит к задержке информативной составляющей на время T/2 или на М/2 отсчетов. От этого недостатка свободен алгоритм

который в силу своей физической нереализуемости может применяться только к накопленному массиву данных. Поэтому информация все равно будет получаться с запаздыванием, но будет привязана к правильному моменту времени.

Алгоритм текущего среднего как в дискретном, так и в непрерывном виде очень прост. Однако он имеет некоторый недостаток. Весовая функция, соответствующая линейному оператору (6) , имеет вид 1, показанный на рис. 5, а, и записывается как

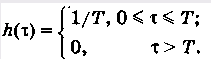
Взяв преобразование Фурье, получим комплексную частотную характеристику, соответствующую этой весовой функции.

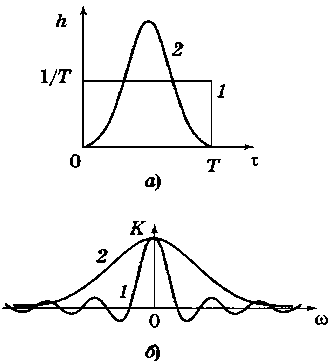
Модуль этой частотной характеристики показан на рис. 5, б (кривая 1). Из ее графика видно, что частотная характеристика (8) существенно неравномерна и на частотах, кратных π/Т, обращается в нуль, то есть сигнал на этих частотах полностью подавляется.

Для улучшения качества сглаживания используются другие весовые функции, отличные от прямоугольной. Тогда оператор текущего среднего в общем случае примет вид

(9)

Весовая функция в (7) должна удовлетворять условию

(10)

которое обеспечивает для постоянного сигнала коэффициент передачи, равный единице. Обычно весовую функцию берут симметричной относительно середины интервала [0; Т], например полином второй или четвертой степени. Получаемая частотная характеристика все равно остается неравномерной и имеет нулевые провалы, но на более высоких частотах. Очень часто в качестве весовой функции оператора текущего среднего используется усеченное нормальное распределение (кривая 2 на рис. 5, а), поскольку преобразование Фурье от нормального распределения имеет ту же форму, а значит, модуль частотной характеристики монотонно убывает и она практически не обращается в нуль (кривая 2 на рис. 5, б).

При замене интеграла (9) суммой отсчеты усредняются с весовыми коэффициентами, близкими к отсчетам весовой функции. Некоторое уточнение требуется для строгого выполнения модифицированного условия (10), в соответствии с которым сумма весовых коэффициентов должна равняться единице.

К задачам сглаживания примыкает задача фильтрации информационного сигнала с энергетическим спектром S_x (w) на фоне шума с энергетическим спектром S_n (w). Частотная характеристика фильтра, обеспечивающего наименьшую среднеквадратичную погрешность воспроизведения информативной составляющей, задается соотношением

(11)

Фазовая характеристика такого фильтра должна быть максимально близка к линейной.

Практическое применение соотношения (11) осложнено необходимостью располагать априорной информацией о спектрах информационной составляющей и локальных возмущений. Однако из этой формулы можно сделать один качественный вывод. Поскольку спектр шума, как правило, более широкополосный, чем спектр информативной составляющей, частотная характеристика, задаваемая (11), соответствует фильтру нижних частот, то есть и в этом случае производится сглаживание первичной информации.

Аналогично с помощью многократных интегралов или многократных сумм можно записать алгоритмы сглаживания по пространству.

Сглаженные функции изменяются медленнее по сравнению с исходными. Поэтому при их дискретизации можно использовать больший интервал, что и уменьшает объем передаваемых данных. Однако следует иметь в виду, что если введение поправок или линеаризация всегда приводят к положительным результатам, то к сглаживанию нужно относиться с осторожностью. При сильном сглаживании можно потерять быстро изменяющиеся компоненты, важные для описания ИО.

Для уменьшения объема обрабатываемых данных сглаживание может проводиться на центральной ЭВМ. Однако это не приведет к уменьшению загрузки каналов связи. В целях уменьшения объема передаваемых данных для сглаживания должны использоваться микропроцессорные устройства, встроенные в ИК.

Выводы

В процессе выполнения контрольной работы мы ознакомились с:

- типовыми алгоритмами сбора измерительной информации;

- введением поправок;

- сглаживанием исходных данных.

Литература

1. Автоматизация физических исследований и эксперимента: компьютерные измерения и виртуальные приборы на основе Lab VIEW / под ред. П. А. Бутыркина. — М.: ДМК-Пресс, 2005.— 264 с.

2. Анисимов Б. В., Голубкин В. Н. Аналоговые и гибридные вычислительные машины. — М.: Высшая школа, 1990., — 289 с.

3. Атамалян Э. Г. Приборы и методы измерения электрических величин. — М.: Дрофа, 2005. — 415 с.

4. Ацюковский В. А. Основы организации системы цифровых связей в сложных информационно-измерительных комплексах. — М.: Энергоатомиздат, 2001. — 97 с.

5. Барский А. Б. Нейронные сети. Распознавание, управление, принятие решений. — М.: Финансы и статистика, 2004. — 176 с.

6. Батоврин В., Бессонов А., Мошкин В. Lab VIEW: Практикум по электронике и микропроцессорной технике. — М.: ДМК-Пресс, 2005 —182 с.

7. Вентцелъ Е. С, Овчаров Л. А. Теория вероятностей и ее инженерные приложения. — М.: Высшая школа, 2007. — 491 с.

8. Волкова В. Н., Денисов А. А. Теория систем. — М.: Высшая школа, 2006. — 511 с.

9. ГОСТ Р 8.596—2002. ГСИ. Метрологическое обеспечение измерительных систем. Основные положения.

10. ГОСТ 16263—70. ГСИ. Метрология. Термины и определения.

11. ГОСТ 26016—81. Единая система стандартов приборостроения. Интерфейсы, признаки классификации и общие требования.

12. ГОСТ 8.437—81. ГСИ. Системы информационно-измерительные. Метрологическое обеспечение. Основные положения.

13. Грановский В. А. Системная метрология: метрологические системы и метрология систем. — СПб.: ГНЦ РФ ЦНИИ "Электроприбор", 1999. — 360 с.

14. Гутников В. С. Интегральная электроника в измерительных устройствах. — Л., 1988. — 304 с.

15. Демидович В. П., Марон И. А. Основы вычислительной математики. — М.: Наука, 1970. — 654 с.

16. Деч Р. Нелинейные преобразования случайных процессов. — М.: Советское радио, 1965. — 208 с.

17. Джексон Р. Г. Новейшие датчики. — М.: Техносфера, 2007.— 384 с.

18. Измерение электрических и неэлектрических величин / Н. Н. Ев-тихиев, Я. А. Купершмидт, В. Ф. Папуловский, В. Н. Скуго-ров; под общ. ред. Н. Н. Евтихиева. — М.: Энергоатомиздат,1990. — 352 с.

19. Информационно-измерительная техника и технологии / В. И. Калашников, С. В. Нефедов, А. Б. Путилин и др.; под ред. Г. Г. Ра-неева. — М.: Высшая школа, 2002. — 454 с.

20. Калабеков В. В. Цифровые устройства и микропроцессорные системы. — М.: Радио и связь, 1997. — 336 с.

21. Карабутов Н. Н. Адаптивная идентификация систем. Информационный синтез. — М.: Едиториал УРСС, 2006. — 384 с.

22. Киреев В. И., Пантелеев А. В. Численные методы в примерах и задачах. — М.: Высшая школа, 2008. — 480 с.

23. Корнеенко В. П. Методы оптимизации. — М.: Высшая школа, 2007. — 664 с.

24. Максимей И. В. Имитационное моделирование на ЭВМ. — М.: Радио и связь, 1988. — 230 с.

25. Мезон С, Циммерман Г. Электронные цепи, сигналы и системы. — М.: Иностранная литература, 1963. — 594 с.

26. Метрологическое обеспечение измерительных информационных систем (теория, методология, организация) / Е. Т. Удовиченко, А. А. Брагин, А. Л. Семенюк и др. — М.: Издательство стандартов, 1991. — 192 с.

27. МИ 2438—97. ГСИ. Системы измерительные. Метрологическое обеспечение. Общие положения.

28. Мячев А. А., Степанов В. Н. Персональные ЭВМ и микроЭВМ. Основы организации. — М.: Радио и связь, 1991. — 320 с.

29. Новоселов О. Н., Фомин А. Ф. Основы теории и расчета информационно-измерительных систем. — М.: Машиностроение,

1991. — 336 с.

30. Островский Ю. И. Голография и ее применение. — М.: Наука, 1976. — 256 с. дискретизация погрешность генератор линеаризация

31. Пантелеев А. В., Летова Т. А. Ме— М.: Высшая школа, 2008. — 544 с.тоды и задачах.

32. Потапов А. С. Распознавание образов и машинное восприятие. — СПб.: Политехника, 2007. — 546 с.

33. Путилин А. Б. Вычислительная техника и программирование в измерительных системах. — М.: Дрофа, 2006. — 416 с.

34. РМГ 29—99. Метрология. Основные термины и определения.

35. Рубичев Н. А., Фрумкин В. Д. Достоверность допускового контроля качества. — М.: Издательство стандартов, 1990. — 172 с.

36. Руководство по выражению неопределенности измерения / под ред. В. А. Слаева. — СПб.: ГП "ВНИИМ им Д. И. Менделеева", 1999. — 126 с.

37. Самарский А. А., Михайлов А. П. Математическое моделирование. — М.: Наука; Физматлит, 1997. — 428 с.

38. Советов Б. Я., Цехановский В. В. Информационные технологии. — М.: Высшая школа, 2008. — 263 с.

39. Уайлд Д. Дж. Методы поиска экстремума. — М.: Наука, 1967. — 268 с.

40. Ушаков И. А. Курс теории надежности систем. — М.: Дрофа, 2008. — 240 с.

41. Фомин Я. А. Теория выбросов случайных процессов. — М.: Связь, 1980. — 216 с.

42. Фрайден Дж. Современные датчики: справочник. — М.: Техносфера, 2005. — 592 с.

43. Фрумкин В. Д., Рубичев Н. А. Теория вероятностей и статистика в метрологии и измерительной технике. — М.: Машиностроение, 1987— 168 с.

44. Хартман К. и др. Планирование эксперимента в исследовании технологических процессов. — М.: Мир, 1977. — 562 с.

45. Цапенко М. П. Измерительные информационные системы. — М.: Энергоатомиздат, 1985. — 357 с.

46. Чистяков В. П. Курс теории вероятностей .— М.: Дрофа, 2007. — 256 с.