ТЕМА
ДИНАМИЧЕСКИЕ СИСТЕМЫ В ПЛОСКОЙ ОБЛАСТИ
1. Введение
Мы будем рассматривать системы дифференциальных уравнений вида
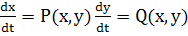 (I) (I)
где Р (х, у) и Q (х, у) — непрерывные функции, определенные в некоторой области Gевклидовой плоскости (х, у — декартовы координаты) и имеющие в этой области непрерывные частные производные до порядка не ниже первого. Область может быть как ограниченной, так и неограниченной. В частности, область Gможет совпадать со всей плоскостью (х, у).
Системы вида (I) являются частным случаем систем двух дифференциальных уравнений с двумя неизвестными функциями: независимое переменное tв их правые части явно не входит. Системы дифференциальных уравнений, правые части которых не содержат явно независимое переменное, называются автономными. Автономные системы дифференциальных уравнений называются также динамическими системами.
Систему (I) мы будем называть динамической системой на плоскости или в плоской области. Мы будем также говорить, что динамическая система задана или определена в области G. В дальнейшем мы будем опускать слова «на плоскости» и «в плоской области».
Динамическая система (I), заданная в области G, называется системой класса Сn
, если функции Р (х, у) и Q(я, у) являются функциями класса Сn
, т. е. имеют в области Gнепрерывные частные производные до порядка nвключительно.
Динамическая система (I) называется системой аналитического класса или аналитической системой, если функции Р и Qявляются аналитическими функциями в области G.
Очевидно, всякая система класса Ck
(к > 1) является одновременно системой класса Ck
1
, где к1
< к, в частности, системой класса C1
. Аналитическая система является системой класса Ck
для любого натурального к.
Все рассматриваемые в этой книге динамические системы являются системами класса  . Поэтому всюду в дальнейшем под динамической системой мы будем во всяком случае всегда подразумевать систему класса . Поэтому всюду в дальнейшем под динамической системой мы будем во всяком случае всегда подразумевать систему класса  , не оговаривая этого явно. , не оговаривая этого явно.
Изложим простейшие свойства динамических систем в плоской области. Свойства эти характерны для автономных систем дифференциальных уравнений. Неавтономные системы (т. е. системы, в правые части которых tвходит явно), вообще говоря, ими не обладают .
2. Геометрическая интерпретация динамической системы (I) в пространстве -R3
Рассмотрим обычную для системы двух дифференциальных уравнений с двумя неизвестными функциями геометрическую интерпретацию, т. е. геометрическую интерпретацию в трехмерном пространстве с декартовыми координатами х, у, t.
Функции Р (х, у) и Q (х, у) нужно при этом рассматривать как функции трех переменных х, у и t. Но так как эти функции от tне зависят, то в трехмерном пространстве R3
областью определения правых частей системы (I) является бесконечная цилиндрическая область Н, образованная всеми прямыми, параллельными оси t, пересекающими плоскость (х, у) в точках области G.
Решения

системы (I) интерпретируются как кривые, расположенные в области Н. Эти кривые называются интегральными кривыми системы (I). Мы будем, здесь и всюду в дальнейшем, под решением системы дифференциальных уравнений подразумевать решение, продолженное на максимальный возможный интервал значений t.
Так как функции Р (х, у) и Q (х, у) во всяком случае являются функциями класса С1
то для системы (I) во всех точках области Hвыполняются условия теоремы существования и единственности, а следовательно и сама эта теорема. Мы сформулируем ее для системы (I) следующим образом:
Теорема 1. Для любой точки М0
(х0
, ) ) Gи для любого t0
, Gи для любого t0
,  , существует одно и только одно решение , существует одно и только одно решение

системы (I), удовлетворяющее начальным условиям

определенное для всех значений t в некотором определенном интервале (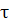 , Т), содержащем t0
.(В частности, решение может быть определено при всех значениях t, т. е. t может быть равно , Т), содержащем t0
.(В частности, решение может быть определено при всех значениях t, т. е. t может быть равно 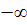 , а Т может быть равно , а Т может быть равно  ). ).
Геометрически теорема 1 означает, что через каждую точку области Н проходит интегральная кривая системы (I) и при этом только одна.
Для системы вида (I) справедлива также следующая теорема, которая существенно используется в дальнейшем:
Теорема 2. Пусть  — замкнутая ограниченная область, содержащаяся в области G ( — замкнутая ограниченная область, содержащаяся в области G (  G), G),
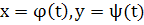 (1) (1)
— решение системы (I), определенное в интервале (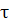 , Т) и такое, что при всех t на интервале ( , Т) и такое, что при всех t на интервале (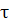 , Т) точка N ( , Т) точка N ( , ,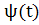 ) все время остается в области ) все время остается в области  . Тогда . Тогда 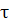 = =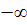 , T=+ , T=+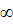 , т.е.решение (1) определено для всех значений t. , т.е.решение (1) определено для всех значений t.
Доказательство. Предположим, что решение

определено при значении t - t0
. Пусть 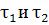 — два произвольных числа, причем — два произвольных числа, причем  < t0
, < t0
,  > t0
. Обозначим через > t0
. Обозначим через 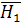 конечную цилиндрическую область пространства конечную цилиндрическую область пространства  , состоящую из всех точек М (t, x, у) таких, что , состоящую из всех точек М (t, x, у) таких, что 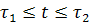 , а х, у таковы, что точка (х, у) , а х, у таковы, что точка (х, у)   (рис. 1). Интегральная кривая, соответствующая решению (1), проходит через точку М0
(t0
, (рис. 1). Интегральная кривая, соответствующая решению (1), проходит через точку М0
(t0
, , , ), принадлежащую области H1
. Но тогда, в силу теоремы (А') дополнения, эта интегральная кривая выходит из области ), принадлежащую области H1
. Но тогда, в силу теоремы (А') дополнения, эта интегральная кривая выходит из области 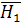 как при значении, большем t0
, так и при значении, меньшем t0
. Однако выйти из цилиндрической области как при значении, большем t0
, так и при значении, меньшем t0
. Однако выйти из цилиндрической области 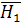 через боковую поверхность этой области интегральная кривая не может, так как в этом случае, очевидно, нашлась бы точка N ( через боковую поверхность этой области интегральная кривая не может, так как в этом случае, очевидно, нашлась бы точка N (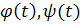 ), лежащая вне замкнутой области ), лежащая вне замкнутой области  , что противоречит условию теоремы. , что противоречит условию теоремы.

Рис. 1.
Следовательно, рассматриваемая интегральная кривая выходит из  через нижнее и верхнее основания (рис. 1). Но это значит, что решение (1) определено при t= через нижнее и верхнее основания (рис. 1). Но это значит, что решение (1) определено при t=  и t = и t = . Так как . Так как 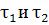 произвольны, то решение (1) определено при всех значениях t. Теорема доказана. произвольны, то решение (1) определено при всех значениях t. Теорема доказана.
3. Простейшие свойства решений системы (I)
Мы установим некоторые cвойства решений системы (I), являющиеся следствием автономности этой системы.
Лемма 1. Если 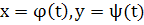
есть решение системы (I), определенное на интервале (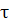 , Т), то , Т), то
 (2) (2)
где С — любая постоянная, также есть решение системы (I) и это решение определено на интервале (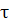 — С, Т — С). — С, Т — С).
Доказательство. Так как (1) есть решение системы (I), то при всех t ( (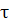 , Т) имеет место тождественное равенство , Т) имеет место тождественное равенство
 ( (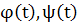 ), ), . .
Если заменить в этих равенствах tна t+C, то при всех t ( (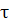 —С,Т — С) мы будем иметь тождественное равенство —С,Т — С) мы будем иметь тождественное равенство
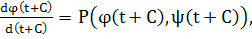
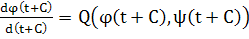 (3) (3)
Но, очевидно
 , , 
и, следовательно, равенства (3) могут быть записаны в виде
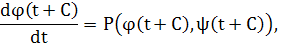

Последние равенства показывают, что функции (2) являются решением системы (I). Тот факт, что это решение определено на интервале (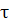 — С, Т — С), устанавливается простым рассуждением, которое мы опускаем. Лемма доказана. — С, Т — С), устанавливается простым рассуждением, которое мы опускаем. Лемма доказана.
С точки зрения геометрической интерпретации в трехмерном пространстве утверждение леммы 1 означает, что линия, получающаяся из любой интегральной кривой путем сдвига ее вдоль оси tна любой отрезок, также есть интегральная кривая. В самом деле, интегральная кривая

получается из интегральной кривой
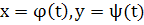
сдвигом вдоль оси tна величину С.
Лемма 2.
а) Решения системы (I)
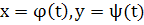 (1) (1)
и  (2) (2)
можно рассматривать как решения, удовлетворяющие начальным условиям с одинаковыми начальными значениями х0
и у0
и различными начальными значениями переменного t.
б) Два решения, удовлетворяющие начальным условиям с одинаковыми начальными значениями переменных х0
, у0
и различными начальными значениями t,могут быть получены одно из другого заменой tна 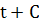 с надлежащим выбором постоянной С. с надлежащим выбором постоянной С.
Доказательство. Если решение (1) соответствует начальным значениям t0
, x0
, у0
так, что
 (3) (3)
то в силу очевидных равенств
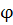 (t0
—С + С) = (t0
—С + С) = 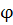 (t0
) = x0
ψ (t0
—С + С) = ψ (t0
) = y0 (t0
) = x0
ψ (t0
—С + С) = ψ (t0
) = y0
решение (2) соответствует начальным значениям t0
—С, х0
, у0
, что и доказывает утверждение а).
Далее, рассмотрим наряду с решением (1), соответствующим начальным значениям t0
, x0
, у0
, решение
 (4) (4)
соответствующее начальным значениям  , x0
, у0
, где , x0
, у0
, где  t0
. Если в решении t0
. Если в решении
(2) 
величину С взять равной t0
— , то оно, очевидно, будет соответствовать тем же начальным значениям , то оно, очевидно, будет соответствовать тем же начальным значениям  , x0
, у0
, что и решение (4). В силу единственности решения, удовлетворяющего данным начальным условиям, отсюда следует , x0
, у0
, что и решение (4). В силу единственности решения, удовлетворяющего данным начальным условиям, отсюда следует
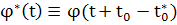 , , 
что и доказывает утверждение б) леммы.
В дальнейшем, рассматривая наряду с решением (1) решение (2), мы будем часто говорить, что рассматриваются решения, отличающиеся выбором начального значения t. Решение всякой системы двух дифференциальных уравнении, соответствующее любым произвольным начальным значениям t0
, х0
, у0
, очевидно, является функцией t, t0
, х0
, у0
, т. е. записывается в виде
х = Ф(t, t0
, х0
, г/о), y= Ψ (t, t0
, х0
, у0
) (5)
При этом по самому смыслу функций Ф (t, t0
, х0
, у0
) и Ψ (t, t0
, x0
, у0
), Ф(t0
, t0
, х0
, у0
) = х0
, Ψ (t0
, t0
, х0
, у0
)= у0
Однако в случае системы (1), вследствие автономности этой системы, функции (5) являются по существу не функциями переменных tи t0
, а функциями разности t—t0
. Это устанавливается в следующей лемме:
Лемма 3. Решение системы (I) как функции от t и от начальных значений t0
, x0
, у0
,может быть записано в виде
x = 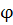 (t—t0
, х0
, у0
), y= ψ(t—t0
, х0
, у0
).(6) (t—t0
, х0
, у0
), y= ψ(t—t0
, х0
, у0
).(6)
Доказательство. Рассмотрим наряду с решением (5) решение
х = Ф(t, 0, х0
, у0
), y =Ψ (t, 0, х0
, у0
),
удовлетворяющие начальным условиям: при t=0, х=х0
, у=у0
В силу леммы 1 функции
x = Ф (t — t0
, 0, х0
, у0
), y =Ψ (t— t0
,0, х0
,у0
) (7)
также являются решением системы (I). Решения (5) и (7) соответствуют одним и тем же начальным значениям t0
, x0
, у0
. Но тогда эти решения совпадают, т. е.
Ф (t ,t0
, х0
, у0
)= Ф (t — t0
, 0, х0
, у0
)
Ψ (t , t0
, х0
,у0
)= Ψ (t— t0
,0, х0
,у0
)
Введение обозначений
Ф (t — t0
, 0, х0
, у0
)= (t—t0
, х0
, у0
), (t—t0
, х0
, у0
),
Ψ (t— t0
,0, х0
,у0
)= ψ(t—t0
, х0
, у0
)
устанавливает справедливость утверждения леммы.
В дальнейшем решение системы (I), соответствующее начальным значениям t0
, х0
, у0
, мы всегда будем записывать в виде (6).
Лемма 4. Если решение
x = 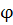 (t—t0
, х0
, у0
), y= ψ(t—t0
, х0
, у0
).(8) (t—t0
, х0
, у0
), y= ψ(t—t0
, х0
, у0
).(8)
определено при значении t= t1
, и
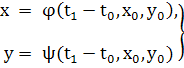 (9) то (9) то
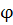 (t—t0
, х0
, у0
) (t—t0
, х0
, у0
) 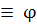 (t—t1
, х0
, у0
) (t—t1
, х0
, у0
)
ψ(t—t0
, х0
, у0
)  (t—t1
, х0
, у0
) (10) (t—t1
, х0
, у0
) (10)
Доказательство. Из соотношений (9), очевидно, следует, что решение (8) и решение
x= (t—t1
, х0
, у0
), y= (t—t1
, х0
, у0
), y= (t—t1
, х0
, у0
) (t—t1
, х0
, у0
)
являются решениями, соответствующими одним и тем же начальным значениям t1
, х1
, y1
. Но тогда эти решения совпадают, т. е. имеют место равенства (10).
Замечание. Полагая в тождествах (10) t = t0
, мы получим
x0
= 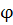 (t0 (t0
 t1
, х1
, у1
) , y0
= ψ(t0 t1
, х1
, у1
) , y0
= ψ(t0
 t1
, х1
, у1
) t1
, х1
, у1
)
Это, очевидно, справедливо при любых t1
, х1
, у1
удовлетворяющих соотношениям (10). Опуская индексы, мы получаем
x0
= (t0
—t, х, у) , y0
= ψ(t0
—t, х, у). (t0
—t, х, у) , y0
= ψ(t0
—t, х, у).
Лемма 5. Если система (I) является системой класса Сn
, тoфункции
x0
= (t—t0
, х0
, у0
) , y0
= ψ (t—t0
, х0
, у0
) (t—t0
, х0
, у0
) , y0
= ψ (t—t0
, х0
, у0
)
при всех значениях, входящих в них переменных, при которых эти функции определены, имеют непрерывные (по совокупности всех переменных) частные производные:
1) по t (или t0
) до порядка n+1 включительно,
2) по х0
и у0
до порядка nвключительно

3). пot(или t0
) и по х0
и у0
—содержащие по крайней мере одно дифференцирование по t (или t0
)—до порядка n + 1
4. Геометрическая интерпретация динамической системы на фазовой плоскости (х, у)
Геометрическая интерпретация системы (I) в трехмерном пространстве (х, у, t) в настоящей книге является вспомогательной. Основная геометрическая интерпретация автономной системы (1)связана с рассмотрением плоскости (х, у). Эта плоскость называется фазовой плоскостью системы (I).
Будем в каждой точке М (х, у) области Gплоскости (х, у) рассматривать вектор vс компонентами Р (х, у), Q(x, у). Динамическая система (I) определяет, таким образом, в области G векторное поле *).
В силу того, что Р (х, у) и Q (х, у) по предположению имеют непрерывные частные производные, векторное поле, определяемое системой (I), является так называемым непрерывно дифференцируемым векторным полем.
Пусть в точке М (х, у) хотя бы одна из величин Р (х, у), Q (х, у) не обращается в нуль. Тогда длина вектора в этой точке

отлична от нуля, а синус и косинус угла 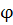 (x, у) между положительным направлением оси х и направлением вектора даются выражениями (x, у) между положительным направлением оси х и направлением вектора даются выражениями

В тех точках, в которых одновременно Р (х, у), Q(x, у).
длина вектора обращается в нуль, а направление вектора становится неопределенным. Такие точки называются особыми точками векторного поля (или особыми точками системы (1)); точки, в которых хотя бы одна из величин Р (x, у), Q (х, у) не равна нулю,— обыкновенными или неособыми точками этого векторного поля. Во всякой неособой точке М векторного поля угол  (x, у), непрерывен. В особой точке угол (x, у), непрерывен. В особой точке угол  (x, у) неопределен, и при стремлении (x, у) неопределен, и при стремлении  и и  к координатам особой точки lim к координатам особой точки lim может не существовать. может не существовать.
Пусть
 (11) (11)
— какое-нибудь решение системы (I). Множество точек М (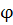 (t), ψ (t)), где tпринимает все значения, при которых определено решение (11), называется траекторией, соответствующей данному решению, а также траекторией векторного поля, заданного динамической системой (І), или просто траекторией данной динамической системы (а также иногда фазовой траекторией). (t), ψ (t)), где tпринимает все значения, при которых определено решение (11), называется траекторией, соответствующей данному решению, а также траекторией векторного поля, заданного динамической системой (І), или просто траекторией данной динамической системы (а также иногда фазовой траекторией).
Уравнения (11), очевидно, являются параметрическими уравнениями траектории. Обратно, если дана какая-нибудь траектория, то решение, которому она соответствует, мы будем называть решением, соответствующим данной траектории.
В математической литературе весьма употребительно векторное обозначение для системы дифференциальных уравнений. Система (I) в этом обозначении запишется в виде векторного уравнения
 = F(x) = F(x)
Векторное обозначение чрезвычайно удобно при рассмотрении систем, состоящих из большого числа уравнении. Однако в рассмотренном нами случае системы только двух дифференциальных уравнении в этом обозначении нет особой необходимости, п мы не будем пользоваться им для того, чтобы не загромождать изложение различными символиками.]
Если точка М (х, у) траектории не является особой точкой векторного поля, то вектор (Р (х, у), Q (х, у)) является касательным вектором к траектории (рис. 2). Действительно, в силу того, что

есть решение системы (I), имеют место тождества
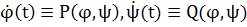 (12) (12)
Но вектор с компонентами 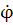 (t), (t),  (t), очевидно, является касательным вектором к траектории, и в силу равенств (12) он совпадает с вектором поля, заданного системой (I). (t), очевидно, является касательным вектором к траектории, и в силу равенств (12) он совпадает с вектором поля, заданного системой (I).

Рассматривая параметр tкак «время», можно дать следующую «кинематическую» интерпретацию системы (I): решение
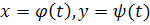
можно рассматривать как закон движения точки по траектории на фазовой плоскости. В каждой точке фазовой плоскости вектор, заданный системой (I), т. е. вектор Р(х, у), Q (х, у), очевидно, равен скорости движущейся точки или «фазовой скорости». Решениям с одними и теми же начальными значениями х0
и у0
и различными начальными значениями t0
соответствуют движения, начинающиеся в одной и той же точке, но в различные начальные моменты «времени» (t0
и t*). Точка с координатами (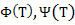 ) называется также «изображающей» или «представляющей» точкой. ) называется также «изображающей» или «представляющей» точкой.
Пусть М (a,b) — особая точка системы (I), так что
P(a,b)=Q(a,b)(13)
Тогда, очевидно, х = a, у = bесть решение системы (I), и, следовательно, особая точка векторного поля сама является отдельной траекторией. Такая траектория называется состоянием равновесия *). Очевидно, также обратно, если у системы (I) есть решение
х = а, y= b(14)
(а и b— некоторые постоянные), то точка a, bнепременно является состоянием равновесия (особой точкой векторного поля), т. е. для нее выполняются равенства (13). Решение (14), очевидно, вследствие того, что tв него не входит, определено для всех t.
В дальнейшем для точек х, у области G, для которых Р (х, у) =0, Q (х, у) = 0, в основном будет использоваться термин «состояние равновесия» (а не особая точка).
Состояние равновесия М (а, Ь) системы (I) называется изолированным, если существует  > 0 такое, что в > 0 такое, что в  -окрестности кроме М не лежит уже более ни одного состояния равновесия. -окрестности кроме М не лежит уже более ни одного состояния равновесия.
5. Разбиение области в фазовой плоскости на траектории
Некоторые элементарные сведения о траекториях.
Лемма 6. Всяким двум решениям, отличающимся только выбором начального значения t0
, соответствует одна и та же траектория.
В другой терминологии — «положением равновесия» или «точкой покоя».
Доказательство. В силу лемм 1 и 2 всякие два решения, отличающиеся выбором начальных значений t0
(но имеющие одни и те же Начальные значения  ), могут быть получены одно из другого заменой tна t+ С. Но если даны два решении ), могут быть получены одно из другого заменой tна t+ С. Но если даны два решении
 (15) (15)
 (16) (16)
причем решение (15) определено на интервале ( , Т), а решение (16) — на интервале ( , Т), а решение (16) — на интервале ( — С, Т — С), то, очевидно, им соответствует одна и та же траектория (так как замена в (15) tчерез t+С является просто заменой обозначении переменного). Лемма доказана. — С, Т — С), то, очевидно, им соответствует одна и та же траектория (так как замена в (15) tчерез t+С является просто заменой обозначении переменного). Лемма доказана.
Теорема 3. Через каждую точку области G проходит одна и только одна траектория динамической системы (1).
Доказательство. Пусть М0
(х0
, у0
) — произвольная точка области G.
Тогда в силу теоремы 1 (о существовании и единственности решения) при всяком tсуществует решение, соответствующее начальным значениям t0
, x0
, 

Это, очевидно, и означает, что через точку х0
, у0
проходит хотя бы одна траектория L.
Предположим теперь, что через одну и ту же точку М0
(х0
, у0
) области Gпроходят две различные траектории Lи L*.
Пусть

— решение, соответствующее траектории L*. Это решение, очевидно, непременно должно быть таким, чтобы при некотором значении t = t* мы имели бы

но тогда в силу леммы 2 при надлежащем выборе С мы должны иметь

и, следовательно (см. лемму 6), траектории Lи L* вопреки предположению не могут быть различны. Теорема доказана.
Замечание 1. Из проведенного в теореме рассуждения непосредственно вытекает, что всякие два различных решения, соответствующих одной и той же траектории, получаются друг из друга заменой tна t+С, т. е. отличаются друг от друга только выбором начального значения t0
(см. лемму 2).
Замечание 2. Пусть при каком-либо выборе решения, соответствующего траектории L, точке М0
этой траектории соответствует значение t0
, а точке M1
— значение t0
+ . Тогда из замечания 1 следует, что если при некотором другом выборе решения, соответствующего траектории L, точке М0
соответствует значение t*, то значению t* + . Тогда из замечания 1 следует, что если при некотором другом выборе решения, соответствующего траектории L, точке М0
соответствует значение t*, то значению t* + соответствует точка соответствует точка  . .
Замечание 3. Если траектория целиком лежит в ограниченной замкнутой области  с G, то в силу теоремы 2 соответствующее ей решение определено при всех значениях с G, то в силу теоремы 2 соответствующее ей решение определено при всех значениях
t(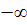 < t< < t< ) )
В силу теоремы 3 динамическая система, заданная в области G, определяет некоторое семейство траекторий или, как мы будем говорить, некоторое разбиение области G на траектории.
Мы укажем здесь некоторые основные свойства траекторий. Выше мы уже останавливались на одном частном типе траекторий, именно, на состояниях равновесия.
Как мы видели, х = а, y=bтогда и только тогда является состоянием равновесия, когда выполняются условия Р(а, b) = Q(a, b) = 0.
Предположим теперь, что траектория L, соответствующая решению

не является состоянием равновесия. Во всех точках такой траектории, очевидно, выполняется неравенство
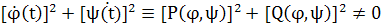
Действительно, если бы в какой-нибудь точке М*(х*, у*) траектории L, соответствующей значению t*, имело место равенство
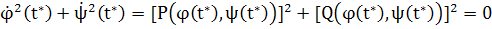
т. е. одновременно

и это, очевидно, означало бы, что точка х*, у* является состоянием равновесия. Но состояние равновесия само является отдельной траекторией, и в силу теоремы 3 точка М* (х*, у*) не может принадлежать отличной от состояния равновесия траектории L.
Рассмотрим вопрос о том, могут ли быть у траектории, отличной от состояния равновесия, «самопересечения», т. е. возможно ли, чтобы существовали значения t1
и t2
, t1
 t2
такие, чтобы соответствующие им точки траектории совпадали. t2
такие, чтобы соответствующие им точки траектории совпадали.
Ответ на этот вопрос дается следующей леммой:
Лемма 7. Пусть траектория L, соответствующая решению
 ( ( < t< T),(17) < t< T),(17)
отлична от состояния равновесия, и пусть существуют значения t, t1
и t2
( < t1
< t2
< T) такие, что < t1
< t2
< T) такие, что
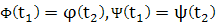
Тогда решение (17) определено при всех значениях
t (т. е.  ) )
функции  , , 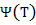 являются периодическими функциями t, а соответствующая траектория—простой гладкой замкнутой кривой. являются периодическими функциями t, а соответствующая траектория—простой гладкой замкнутой кривой.
Доказательство. Пусть
 (18) (18)
Рассмотрим наряду с решением (17) решение
 (19) (19)
определенное на интервале
( — С, Т — С) — С, Т — С)
где С = t2
— t1
(см. лемму 1).
Из равенств (18) следует, что решения (17) и (19) удовлетворяют одним и тем же начальным условиям (при t= t1
, x = х0
, у =у0
). Но тогда эти решения совпадают, а следовательно, совпадают интервалы значений t, на которых они определены. Но интервалы ( , Т) и ( , Т) и ( — С, Т — С) при С — С, Т — С) при С 0 могут совпадать лишь в том случае, когда 0 могут совпадать лишь в том случае, когда  =- =- , Т =+ , Т =+ . .
Таким образом, мы показали, что решения (17) и (19) определены для всех t( < t< < t<  ). Далее, из совпадения решений (17) и (19) следует, что при всех t (— ). Далее, из совпадения решений (17) и (19) следует, что при всех t (— < t< < t<  ) )
 (20) (20)
где C = t2
— t1
>0. Это, очевидно, означает, что функции  (t) и (t) и  (t)— периодические функции с общим периодом 0 = t2
— t1
. Пусть (t)— периодические функции с общим периодом 0 = t2
— t1
. Пусть
 )(21) )(21)
— наименьшее положительное число, при котором имеют место равенства
 (22) (22)
Такое число непременно существует. Действительно, в противном случае можно было бы указать последовательность положительных чисел { } таких, что } таких, что
 и и 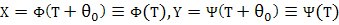
Очевидно, тогда при любом nи любом целом |k|

или, зафиксировав какое-нибудь t0
, можно написать

Таким образом, каждая из функции  (t) и (t) и  (t) принимает одно и то же значение, равное соответственно (t) принимает одно и то же значение, равное соответственно  ( ( ) и ) и  ( ( ) при всех следующих значениях t ) при всех следующих значениях t

где N может быть любым целым числом, а  сколь угодно мало при достаточно большом n. Следовательно, какое бы значение t* мы ни взяли, либо t* =t сколь угодно мало при достаточно большом n. Следовательно, какое бы значение t* мы ни взяли, либо t* =t и тогда и тогда 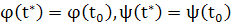 , либо t* попадает в некоторый интервал (t0
+(k-1) , либо t* попадает в некоторый интервал (t0
+(k-1) ,t0
+ ,t0
+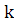  ) или ) или
(t0
—(k-1) ,t0
-- ,t0
--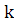  ) и в силу того, что Qn
сколь угодно мало при достаточно большом n, существуют сколь угодно близкие к t* значения t', при которых ) и в силу того, что Qn
сколь угодно мало при достаточно большом n, существуют сколь угодно близкие к t* значения t', при которых

Но тогда в силу непрерывности функций  (t), (t), 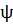 (t) мы, очевидно, также имеем (t) мы, очевидно, также имеем

Это означает, что функции  (t), (t), 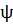 (t)— постоянные, т. е. траектория Lсостояние равновесия, что противоречит условию теоремы. (t)— постоянные, т. е. траектория Lсостояние равновесия, что противоречит условию теоремы.
Очевидно, все точки траектории Lмогут быть получены при изменении tв уравнениях (17) от t0
до t0
+  0
(t0 0
(t0
 t t t0
- t0
- 0
), где t0
— любое фиксированное число. Так как по самому определению 0
), где t0
— любое фиксированное число. Так как по самому определению  0
есть наименьшее число,при котором выполняются равенства(22),то всяким двум значениям 0
есть наименьшее число,при котором выполняются равенства(22),то всяким двум значениям  и t", t0 и t", t0
 заведомо соответствуют различные точки траектории L. Это и означает, что траектория Lявляется простой замкнутой кривой. В силу леммы 5 эта замкнутая кривая, очевидно, гладкая. Таким образом, лемма доказана. заведомо соответствуют различные точки траектории L. Это и означает, что траектория Lявляется простой замкнутой кривой. В силу леммы 5 эта замкнутая кривая, очевидно, гладкая. Таким образом, лемма доказана.
Решение, в котором функции  (t) и (t) и 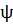 (t) — периодические функции t, называется периодическим решением. Наименьшее число (t) — периодические функции t, называется периодическим решением. Наименьшее число  0
> 0, при котором выполняются равенства (22),— периодом этого решения. 0
> 0, при котором выполняются равенства (22),— периодом этого решения.
Траектория L, соответствующая периодическому решению, называется замкнутой траекторией. Очевидно, все решения, соответствующие данной замкнутой траектории, являются периодическими решениями с одним и тем же периодом. Всякая траектория, не являющаяся замкнутой траекторий или состоянием равновесия, называется незамкнутой траекторией.
Из леммы 7 следует, что у траекторий системы (I) не может быть «самопересечений», т. е. что всякая часть незамкнутой траектории, соответствующая значениям tв любом конечном сегменте, является простой гладкой дугой.
Таким образом, мы получили следующие основные элементарные сведения о траекториях. Траектория может быть: 1) состоянием равновесия, 2) замкнутой траекторией, 3) незамкнутой (несамопересекающейся) траекторией. Эти сведения являются предварительными, так как возможный характер незамкнутых траекторий остается невыясненным.
6. Сопоставление геометрической интерпретации в пространстве R3
и геометрической интерпретации на фазовой плоскости
Как мы уже указывали, каждому решению системы (I) соответствует в 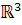 интегральная кривая. интегральная кривая.
Траектория, очевидно, является проекцией этой интегральной кривой на плоскость (x, у). Из леммы 4 следует, что в траекторию проектируются те и только те интегральные кривые пространства 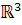 , которые получаются из одной такой кривой (и, следовательно, друг из друга) сдвигом на произвольный отрезок вдоль оси t. Таким образом, устанавливается естественное соответствие между траекториями динамической системы на фазовой плоскости и интегральными кривыми в пространстве , которые получаются из одной такой кривой (и, следовательно, друг из друга) сдвигом на произвольный отрезок вдоль оси t. Таким образом, устанавливается естественное соответствие между траекториями динамической системы на фазовой плоскости и интегральными кривыми в пространстве 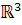 . При этом могут представиться следующие случаи в зависимости от характера траектории L: . При этом могут представиться следующие случаи в зависимости от характера траектории L:
Lесть состояние равновесия М (а, Ь). Соответствующая интегральная кривая в 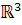 является прямой х = а, у = b, параллельной оси tи проходящей через точку М. При сдвиге вдоль оси tэта прямая переходит сама в себя. является прямой х = а, у = b, параллельной оси tи проходящей через точку М. При сдвиге вдоль оси tэта прямая переходит сама в себя.
2) Lесть замкнутая траектория, соответствующая решению с периодом  0
. Соответствующие интегральные кривые имеют характер «винтовых линий» с шагом 0
. Соответствующие интегральные кривые имеют характер «винтовых линий» с шагом  0
и проектируются в траекторию L. При сдвиге вдоль оси tна отрезок С каждая интегральная кривая переходит в другую кривую, если С не кратно 0
и проектируются в траекторию L. При сдвиге вдоль оси tна отрезок С каждая интегральная кривая переходит в другую кривую, если С не кратно  0
, и сама в себя, если С кратно 0
, и сама в себя, если С кратно  0
(рис. 3). 0
(рис. 3).
3) L— незамкнутая траектория. Каждая интегральная кривая, соответствующая траектории L, при любом сдвиге вдоль оси t, отличном от нулевого, переходит в другую интегральную кривую (рис. 4).

Рис. 3. Рис. 4.
Подчеркнем следующие элементарные факты. Точка, двигаясь по траектории, отличной от состояния равновесия (т. е. «изображающая точка» с координатами х =  (t), y= (t), y= 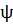 (t) ), не может стремиться к точке какой-либо отличной от нее траектории при t, стремящемся к конечному значению. Действительно, в противном случае , интегральные кривые в пространстве (x, у, t) пересекались бы, что невозможно в силу теоремы 1. В частности, точка, двигаясь по траектории, отличной от состояния равновесия, может стремиться к состоянию равновесия либо при t (t) ), не может стремиться к точке какой-либо отличной от нее траектории при t, стремящемся к конечному значению. Действительно, в противном случае , интегральные кривые в пространстве (x, у, t) пересекались бы, что невозможно в силу теоремы 1. В частности, точка, двигаясь по траектории, отличной от состояния равновесия, может стремиться к состоянию равновесия либо при t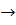  , либо при , либо при 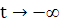
7. Направление на траектории. Изменение параметризации
Пусть L— траектория системы (I) и
х =  (t), y = (t), y = 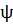 (t) (t)
— какое-нибудь соответствующее ей решение.
Мы введем на траектории Lопределенное направление в качестве положительного. Именно, будем считать положительным направлением на Lнаправление в сторону возрастания t. При таком определении можно сказать, что положительное направление в каждой точке траектории Lсовпадает с направлением вектора, заданного в этой точке системой (I).
Пользуясь «кинематической» интерпретацией, можно сказать, что положительное направление на Lесть то направление, в котором точка с координатами х =  (t), y = (t), y = 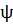 (t) движется по траектории при возрастании tи при котором направление ее скорости в каждой точке совпадает с направлением фазовой скорости. (t) движется по траектории при возрастании tи при котором направление ее скорости в каждой точке совпадает с направлением фазовой скорости.
Введенное таким образом положительное направление на Lне зависит от того, какое из решений, соответствующих траектории L, мы возьмем (так как все такие решения получаются одно из другого заменой tна 
В дальнейшем мы будем обычно опускать слово «положительное», т. е. под направлением на траектории L системы (I) мы будем подразумевать положительное направление, определяемое (или, как говорят, индуцируемое) на L этой системой.
Рассмотрим наряду с системой (I) систему
 (I') (I')
Векторное поле системы (I') получается из векторного поля системы (I), если изменить направление каждого вектора на противоположное (не меняя длин векторов).
Непосредственной проверкой устанавливается, что каждому решению
х =  (t), y = (t), y = 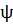 (t) (23) (t) (23)
системы (I) соответствует решение
х =  (-t), y = (-t), y = 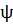 (-t)(24) (-t)(24)
системы (I'). Отсюда очевидно, что системы (I) и (1') имеют одинаковые траектории, но индуцируют на траекториях противоположные направления. Таким образом, переход от системы (I) к системе (I') можно рассматривать, как изменение параметризации на траекториях, именно, как замену параметра tпараметром —t.
Рассмотрим более общий случай изменения параметризации на траекториях системы (1). Пусть f(х, у) — функция класса C1
, заданная в области G. Предположим, что функция f(х, у) отлична от нуля во всех точках области G, отличных от состояний равновесия системы (1), и имеет в них один и тот же знак.
Рассмотрим наряду с системой (I) систему
 (I*) (I*)
В силу предположений, сделанных относительно функции f(х, у), очевидно, что состояния равновесия системы (I) совпадают с состояниями равновесия системы (I*).
Лемма 8. Если
х =  (t), y = (t), y = 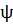 (t)(25) (t)(25)
есть решение системы (I), причем соответствующая ему траектория отлична от состояния равновесия, то существует монотонная функция класса C1
(t) = (s) такая, что пара функций (s) такая, что пара функций
 (26) (26)
является решением системы (I*).
Доказательство. Задавая какое-нибудь начальное значение t0
, t0
 ( ( , Т), где ( , Т), где ( , Т) — интервал определения решения (25), и произвольное s0
, рассмотрим следующую функцию s(t) , Т) — интервал определения решения (25), и произвольное s0
, рассмотрим следующую функцию s(t)

Так как f(х, у) не обращается в нуль в точках, отличных от состояний равновесия, то s(t) является монотонной функцией класса С1
, определенной на интервале ( , Т). Очевидно, существует обратная функция , Т). Очевидно, существует обратная функция
 (s), определенная в некотором интервале ( (s), определенная в некотором интервале ( S), также класса С1
, монотонная. Очевидно, S), также класса С1
, монотонная. Очевидно,

Поэтому
 (27) (27)
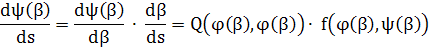

Последние соотношения показывают, что функции (26) являются решением системы (I*). Нетрудно видеть, что ( S), является максимальным интервалом определения решения (26), так как в противном случае интервал ( S), является максимальным интервалом определения решения (26), так как в противном случае интервал ( , Т) не был бы максимальным для решения (25). Лемма доказана. , Т) не был бы максимальным для решения (25). Лемма доказана.
Уравнения (25) и (26) являются, очевидно, различными параметрическими уравнениями одной и той же траектории. Поэтому из леммы 8 следует, что динамические системы (I) и (I*) имеют одни и те же траектории, но с различными параметризациями на них. При переходе от системы (I) к системе (I*) направления на траекториях остаются неизменными, если f(х, у) > 0, и меняются, если F(x,y)<0.
Предположим теперь, что функция f(х, у) может обращаться в нуль в точках, отличных от состояний равновесия системы (I), а также может менять знак в области G. Рассмотрим снова систему (I*). Очевидно, состояниями равновесия системы (I*) являются все состояния равновесия системы (I), а также все точки области G, которые не являются состояниями равновесия системы (1), но в которых f(х, у) = 0.
Кривая f(х, у) = 0 называется особой линией системы (I*) (каждая точка этой кривой является состоянием равновесия системы (I*)).
Рассмотрим теперь траекторию Lсистемы (I), отличную от состояния равновесия. Если на траектории Lфункция f(х, у) 0, то так же, как и выше, Lявляется траекторией системы (I*) с измененной, вообще говоря, параметризацией. 0, то так же, как и выше, Lявляется траекторией системы (I*) с измененной, вообще говоря, параметризацией.
Если же на траектории Lимеются точки кривой f(х, у) = 0, то все точки L, отличные от этих точек, распадаются, как легко видеть, на конечное или счетное число гладких кривых, являющихся траекториями системы (I*) (рис. 5). Направление на каждой такой траектории совпадает с направлением на L, если на этой траектории f(х, у) > 0, и не совпадает в противном случае.
Таким образом, каждая траектория системы (I) либо является траекторией системы (I*), либо состоит из конечного или бесконечного множества траекторий системы (I*) .
В дальнейшем, в ряде предложений и в примерах мы неоднократно будем встречаться с динамическими системами вида
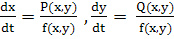 ( (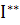 ) )
где Р (х, у), Q (х, у) — функции класса CN
( > 1) или аналитические, f(х, y) — функция класса CN
или аналитическая, которая может обращаться в нуль в области G(в которой рассматривается система). Очевидно, в точках, где (х, у) = 0, правые части рассматриваемой системы (I**) не определены. Однако при указанном виде правых частей можно путем замены параметра tпривести рассмотрение системы (I**) к рассмотрению системы вида (I). > 1) или аналитические, f(х, y) — функция класса CN
или аналитическая, которая может обращаться в нуль в области G(в которой рассматривается система). Очевидно, в точках, где (х, у) = 0, правые части рассматриваемой системы (I**) не определены. Однако при указанном виде правых частей можно путем замены параметра tпривести рассмотрение системы (I**) к рассмотрению системы вида (I).
Действительно, полагая при х и у, необращающих в нуль f(х, у), dt=f(х, у) d , мы получаем систему , мы получаем систему
 (I***) (I***)
Эту же систему мы будем рассматривать при х и у, обращающих в нуль функцию f(х, у) (что соответствует доопределению по непрерывности), так что система (I***) будет определена во всей области G. Очевидно, во всякой части области G, в которой f(х, у) не обращается в нуль, траектории системы (I**) и (I***) совпадают как точечные множества, однако, параметры на них различны. При этом там, где f(х, у) > 0, направление по  совпадает с направлением по t, а там, где f(х, у) < 0 — противоположно ему. Точки с координатами х и у, обращающими в нуль функцию f(х, у), в которых правые части системы (I**) не определены, естественно выделять и считать не принадлежащими траекториям системы (I**) (к таким точкам, как нетрудно убедиться на простых примерах, точка по траектории может стремиться при t, стремящемся к конечному значению). совпадает с направлением по t, а там, где f(х, у) < 0 — противоположно ему. Точки с координатами х и у, обращающими в нуль функцию f(х, у), в которых правые части системы (I**) не определены, естественно выделять и считать не принадлежащими траекториям системы (I**) (к таким точкам, как нетрудно убедиться на простых примерах, точка по траектории может стремиться при t, стремящемся к конечному значению).
8. Терминология и обозначения
В случае, когда решения, соответствующие данной траектории L, определены для всех значении t( ), мы будем иногда, желая подчеркнуть это, называть такую траекторию L целой траекторией. В силу теоремы 2 всякая траектория, лежащая в ограниченйой части плоскости, у которой расстояние любой ее точки от границы области Gбольше некоторого ), мы будем иногда, желая подчеркнуть это, называть такую траекторию L целой траекторией. В силу теоремы 2 всякая траектория, лежащая в ограниченйой части плоскости, у которой расстояние любой ее точки от границы области Gбольше некоторого  0
> 0, заведомо является целой траекторией. 0
> 0, заведомо является целой траекторией.
Обратное неверно. Траектория, у которой есть точки, сколь угодно близкие к границе области G, может как быть, так и не быть целой траекторией.
Пусть М0
— точка траектории L, которая при выбранном решении соответствует значению t= t0
. Если решение определено при всех t(t> t0
), то множество точек траектории L, соответствующих значениям t> t0
, называется положительной полутраекторией, выделенной из траектории L, и обозначается через L(+)
или  . Аналогично если решение определено при всех t . Аналогично если решение определено при всех t t0
, то множество точек траектории L, соответствующих значениям t t0
, то множество точек траектории L, соответствующих значениям t t0
, называется отрицательной полутраекторией, выделенной из траектории L, и обозначается через t0
, называется отрицательной полутраекторией, выделенной из траектории L, и обозначается через  или или  . Очевидно, если взять другое решение, соответствующее траектории L, при котором точке М0
соответствует значение t1 . Очевидно, если взять другое решение, соответствующее траектории L, при котором точке М0
соответствует значение t1
 t0
, то точки полутраектории t0
, то точки полутраектории  (или (или  ) будут соответствовать значениям ) будут соответствовать значениям  . Точку М0
мы иногда будем называть «концом» полутраектории. В дальнейшем нам часто придется рассматривать полутраекторию без указания на то, является ли она положительной или отрицательной. В этом случае мы будем обозначать полутраекторию через U' или L\j0
. В случае, когда траектория Lявляется состоянием равновесия или замкнутой траекторией, всякая положительная и всякая отрицательная полутраектория, выделенная из нее, совпадает с ней самой. Полутраекторию, выделенную из незамкнутой траектории, мы будем называть незамкнутой полу траекторией, а полутраекторию, выделенную из замкнутой траектории (очевидно, совпадающую с этой траекторией), будем называть замкнутой полутраекторией. . Точку М0
мы иногда будем называть «концом» полутраектории. В дальнейшем нам часто придется рассматривать полутраекторию без указания на то, является ли она положительной или отрицательной. В этом случае мы будем обозначать полутраекторию через U' или L\j0
. В случае, когда траектория Lявляется состоянием равновесия или замкнутой траекторией, всякая положительная и всякая отрицательная полутраектория, выделенная из нее, совпадает с ней самой. Полутраекторию, выделенную из незамкнутой траектории, мы будем называть незамкнутой полу траекторией, а полутраекторию, выделенную из замкнутой траектории (очевидно, совпадающую с этой траекторией), будем называть замкнутой полутраекторией.
В математической литературе решение системы (I) часто называют движением. Эта терминология находится в соответствии с «кинематическим» истолкованием динамической системы. Мы также будем пользоваться этой весьма употребительной терминологией. Таким образом, мы будем говорить о движении, соответствующем данным начальным значениям, о траектории, соответствующей данному движению, о движении, соответствующем данной траектории, или, иначе, о движении на траектории (т. е. о решении, соответствующем данной траектории), о периодическом движении и т. д.
Будем также говорить, что траектория L при t = t0
проходит через точку М0
, подразумевая при этом, что на траектории Lвыбрано некоторое определенное движение и при этом движении точке М0
соответствует значение t = t0
. Точно так же мы будем говорить: «точка М1
траектории Lсоответствует значению t= t1
» или «траектория при t= t1
пересекает данную дугу  и т. д., подразумевая под этим, что при данном выбранном движении на L точка М1
или общая точка траектории Lи дуги и т. д., подразумевая под этим, что при данном выбранном движении на L точка М1
или общая точка траектории Lи дуги  соответствует значению t= t1
и т. д. соответствует значению t= t1
и т. д.
Мы будем часто пользоваться следующими выражениями: «траектория Lпри возрастании (или убывании) входит в данную область или выходит из данной области», «траектория при t> T0
остается в данной области» и другими аналогичными выражениями, не требующими пояснения. Кроме того, укажем следующие обозначения. Если
х =  (t), y = (t), y =  (t)(28) (t)(28)
— какое-нибудь движение (т. е. решение), то точку с координатами  (t), (t),  (t) мы будем обозначать через М (t) и решение (28) — через М=М (t). Если указаны начальные значения, которым соответствует рассматриваемое движение, т. е. движение (решение) записано в виде (t) мы будем обозначать через М (t) и решение (28) — через М=М (t). Если указаны начальные значения, которым соответствует рассматриваемое движение, т. е. движение (решение) записано в виде
x= (t — t0
, х0
, у0
) , y = (t — t0
, х0
, у0
) , y =  (t — t0
, х0
, у0
), (29) (t — t0
, х0
, у0
), (29)
то, обозначая через М0
точку х0
, у0
, мы будем записывать точку с координатами  (t—t0
, х0
, у0
), (t—t0
, х0
, у0
),  (t — t0
, х0
, у0
) в виде М (t — t0
, M0
) и решение (29) —в виде М = М (t — t0
, M0
). (t — t0
, х0
, у0
) в виде М (t — t0
, M0
) и решение (29) —в виде М = М (t — t0
, M0
).
9. Теорема о непрерывной зависимости от начальных значений
Наряду с теоремой о существовании и единственности решения основной теоремой теории дифференциальных уравнений является теорема о непрерывной зависимости от начальных значений.
Мы сформулируем здесь эту теорему для рассматриваемых нами автономных систем вида (I).
Теорема 4. Пусть
x= (t — t0
, х0
, у0
) , y = (t — t0
, х0
, у0
) , y =  (t — t0
, х0
, у0
) (t — t0
, х0
, у0
)
— решение системы (I), определенное на интервале ( , Т), а , Т), а  и и  ( ( < <  ) — два произвольных числа из этого интервала. Тогда, каково бы ни было ) — два произвольных числа из этого интервала. Тогда, каково бы ни было  > 0, существует такое > 0, существует такое  > 0, что, если > 0, что, если

то решение x =  (t — t0
, (t — t0
, 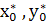 ), y = ), y =  (t — t0
, (t — t0
, 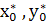 ) определено при всех значениях t, ) определено при всех значениях t,  t t  при всех этих значениях t выполняются неравенства при всех этих значениях t выполняются неравенства
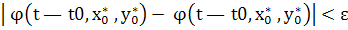
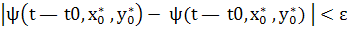
Замечание. Функции  (t— t0
, x0
, y0
), (t— t0
, x0
, y0
),  (t— t0
, x0
, y0
) по самому своему определению являются непрерывными функциями t— t0
. (t— t0
, x0
, y0
) по самому своему определению являются непрерывными функциями t— t0
.

Рис. 6.
Так как в силу настоящей теоремы эти функции непрерывны по переменным х0
, у0
и равномерно непрерывны относительно tна всяком замкнутом конечном промежутке значений t, то, очевидно, эти функции непрерывны по совокупности своих аргументов при всех тех значениях этих аргументов, при которых они определены.
Теорема 4 может быть также сформулирована в следующей геометрической форме, которой мы в основном будем пользоваться в дальнейшем.
Теорема 4'. Пусть
М0
(х0
, у0
) и M1
(x1
y1
)
— две точки произвольной траектории L, соответствующие значениям t0
и t1
переменного t. Тогда для любого  > 0 можно указать такое > 0 можно указать такое  > 0, что если точка М'0 > 0, что если точка М'0
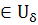 (М0
), то проходящая через эту точку при t= t0
траектория L' определена для всех t в промежутке (М0
), то проходящая через эту точку при t= t0
траектория L' определена для всех t в промежутке  (или t0 (или t0
 ) и точка М' траектории L', соответствующая любому значению t из этого промежутка, лежит в ) и точка М' траектории L', соответствующая любому значению t из этого промежутка, лежит в  -окрестности точки М траектории L, соответствующей тому же t(рис. 6). -окрестности точки М траектории L, соответствующей тому же t(рис. 6).
Докажем лемму, непосредственно вытекающую из теоремы 4.
Лемма 9. Пусть К — замкнутое ограниченное множество, целиком лежащее в G. Всегда существует h0
> 0 такое, что при любом t0
решение
x=  (t — t0
, x0
, y0
), y= (t — t0
, x0
, y0
), y= (t — t0
, x0
, y0
) (30) (t — t0
, x0
, y0
) (30)
для любой точки М0
(х0
, у0
)  К заведомо определено при всех значениях t из промежутка К заведомо определено при всех значениях t из промежутка
t0
- h t t t0
+h. t0
+h.
Доказательство. Предположим, что лемма несправедлива, т. е. для любого h> 0 найдется такая точка М  К, что решение (30), которое мы для краткости запишем в виде M = M(t — t0
, К, что решение (30), которое мы для краткости запишем в виде M = M(t — t0
,  ), не определено на всем сегменте [t0
— h, t0
+ h]. Тогда существует последовательность стремящихся к нулю положительных чисел { ), не определено на всем сегменте [t0
— h, t0
+ h]. Тогда существует последовательность стремящихся к нулю положительных чисел {  } и последовательность точек { } и последовательность точек {  } множества К таких, что решение M = M(t — t0
, } множества К таких, что решение M = M(t — t0
, 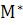 ) не определено на всем сегменте [t0
— hn
, t0
+ hn
]. Так как по предположению К — замкнутое ограниченное множество, то из { ) не определено на всем сегменте [t0
— hn
, t0
+ hn
]. Так как по предположению К — замкнутое ограниченное множество, то из {  } всегда можно выбрать последовательность, сходящуюся к некоторой точке М* множества К. Поэтому мы можем без ограничения общности считать, что сама последовательность { } всегда можно выбрать последовательность, сходящуюся к некоторой точке М* множества К. Поэтому мы можем без ограничения общности считать, что сама последовательность {  } сходится к некоторой точке M* } сходится к некоторой точке M*  К. Рассмотрим решение M = M(t—t0
, М*). Всегда существует h* > 0 такое, что это решение во всяком случае определено при значениях tна сегменте [t0
—h*, t0
+ h*]. В силу теоремы 4 тогда и всякое решение К. Рассмотрим решение M = M(t—t0
, М*). Всегда существует h* > 0 такое, что это решение во всяком случае определено при значениях tна сегменте [t0
—h*, t0
+ h*]. В силу теоремы 4 тогда и всякое решение
M=M(t — t0
, Mn
)
при достаточно большом nопределено на сегменте [t0
— h*, t0
+ h*]. Hohn
< h* при достаточно большом n(так как hn
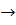 0), и, следовательно, решение М = М (t— t0
, Mn
) должно быть определено при всех значениях tиз сегмента [t0
— hn
, t0
+ hn
], что противоречит выбору точек Мn
. Лемма доказана. 0), и, следовательно, решение М = М (t— t0
, Mn
) должно быть определено при всех значениях tиз сегмента [t0
— hn
, t0
+ hn
], что противоречит выбору точек Мn
. Лемма доказана.
10. Замена переменных
Предположим, что область определения Gсистемы (I) ограничена, и рассмотрим регулярное отображение этой области на некоторую область G* плоскости (и, v).
Пусть это отображение задается формулами
x=f(u, v), y = g(и, v)(Т)
или эквивалентными им формулами
x = f*(x,y), y=g*(x,y), (Т*)
где функции f, g, f*, g* являются функциями класса С2
. Мы будем предполагать также, что G* — ограниченная область; для этого необходимо и достаточно, чтобы функции f* и g* были ограниченными в области G.
Переменные и и vможно рассматривать, как известно, не только как декартовы координаты на плоскости (и, v), но и как криволинейные координаты в области Gплоскости (х, у). Тогда (Т) и (Т*) являются формулами замены переменных или преобразования координат.
Пусть после перехода к координатам и, vсистема (I) принимает вид
 = U(u,v), = U(u,v),  = V(u,v).(31) = V(u,v).(31)
При этом мы имеем, очевидно,
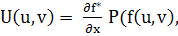 g(u, v)) + g(u, v)) +  Q(f(u, v), g(u,v)), (32) Q(f(u, v), g(u,v)), (32)
V(u, v) =  P(f(u, v), g(u, v)) + P(f(u, v), g(u, v)) + 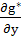 Q(f(u, v), g(u, v)). Q(f(u, v), g(u, v)).
Таким образом, при переходе к новым координатам и, vвектор т с координатами Р (х, у), Q (х, у) преобразуется в вектор т* с координатами U (и, v), V (и, и), связанными с Р (х, у), Q (х, у) выражениями (32).
При отображении (Т) всякая траектория системы (I)
x =  (t), y = (t), y =  (t) переходит в траекторию системы (31) (t) переходит в траекторию системы (31)
 (33) (33)
и, обратно, при отображении (Т*) траектории системы (31) переходят в траектории системы (I). Нетрудно убедиться непосредственно, что пара функций (33) является решением системы (31).
В дальнейшем мы будем рассматривать не только регулярные преобразования координат. В частности, мы часто будем пользоваться переходом к полярной системе координат, который, очевидно, не является регулярным преобразованием координат.
Действительно, при преобразовании к полярным координатам
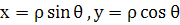
во-первых нарушается взаимная однозначность, а во-вторых функциональный детерминант
 ,обращается в нуль, при ,обращается в нуль, при 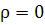
11. Дифференциальное уравнение, соответствующее динамической системе
Если разделить одно уравнение системы (I) на другое, то мы получим либо дифференциальное уравнение
 (II) (II)
либо дифференциальное уравнение
 . ( . ( ) )
Рассмотрим сначала уравнение (II). Пусть  какая-нибудь точка области G. В силу теоремы о существовании и единственности решения, если при значениях какая-нибудь точка области G. В силу теоремы о существовании и единственности решения, если при значениях  , P( , P( ) ) , то существует единственное решение y=f(x), соответствующее начальным значениям , то существует единственное решение y=f(x), соответствующее начальным значениям  , и, следовательно единственная интегральная кривая уравнения (II), проходящая через точку , и, следовательно единственная интегральная кривая уравнения (II), проходящая через точку 
В каждой точке этой кривой угловой коэффициент касательной задается уравнением (II).
Пусть
х =  (t), у = (t), у =  (t) (t)
— решение системы (I), соответствующее начальным значениям t0
, x0
y0
. Выражая tвблизи значений t0
, х0
, у0
как функцию х, t= (х) (это возможно в силу того, что по условию (х) (это возможно в силу того, что по условию  ' (t0
) = Р (x0
,y0
) ' (t0
) = Р (x0
,y0
)  0) и подставляя в функцию у = 0) и подставляя в функцию у = (t), мы, как нетрудно видеть, получаем решение уравнения (II) (t), мы, как нетрудно видеть, получаем решение уравнения (II)
y =  ( ( (x)) = f(x) (x)) = f(x)
Очевидно, интегральная кривая уравнения (II) в точках, в которых она определена, совпадает с траекторией системы (I) или является частью этой траектории.

Рис. 7
Предположим, что решение у = f (х) определено на интервале (x1
, x2
) , и пусть х стремится к одному из концов этого интервала, например х  x1
(все сказанное в этом случае может быть повторено для случая, когда х x1
(все сказанное в этом случае может быть повторено для случая, когда х х2
). На основании общих теорем нетрудно видеть, что если при х х2
). На основании общих теорем нетрудно видеть, что если при х  x1
точка с координатами (x, f(х)) не стремится к границе области G, то она стремится к точке М (x1
, f (x1
)), для которой Р (x1
, f (x1
)) = 0, т. е. к точке, в которой уравнение (II) теряет смысл. Если при этом Q(x1
, f (x1
)) x1
точка с координатами (x, f(х)) не стремится к границе области G, то она стремится к точке М (x1
, f (x1
)), для которой Р (x1
, f (x1
)) = 0, т. е. к точке, в которой уравнение (II) теряет смысл. Если при этом Q(x1
, f (x1
))  0, то точка М, очевидно, является такой точкой траектории системы (I), в которой касательная параллельна оси у (рис. 7). В окрестности такой точки естественно рассматривать уравнение (II*), и как «продолжение» интегральной кривой, соответствующей данному решению у = f(x) уравнения (II), рассматривать интегральную кривую уравнения (II*), проходящую через точку М(x1
, f (x1
)) . Очевидно, в окрестности всякой точки, в которой ни Р (х, у), ни Q (х, у) не обращается в нуль, решение уравнения (II*) может быть получено из решения у = f (х) уравнения (II), если в нем х выразить как функцию у, х =g (у), а части соответствующих интегральных кривых уравнений (II) и (II*), лежащие в достаточно малой окрестности такой точки, совпадают. 0, то точка М, очевидно, является такой точкой траектории системы (I), в которой касательная параллельна оси у (рис. 7). В окрестности такой точки естественно рассматривать уравнение (II*), и как «продолжение» интегральной кривой, соответствующей данному решению у = f(x) уравнения (II), рассматривать интегральную кривую уравнения (II*), проходящую через точку М(x1
, f (x1
)) . Очевидно, в окрестности всякой точки, в которой ни Р (х, у), ни Q (х, у) не обращается в нуль, решение уравнения (II*) может быть получено из решения у = f (х) уравнения (II), если в нем х выразить как функцию у, х =g (у), а части соответствующих интегральных кривых уравнений (II) и (II*), лежащие в достаточно малой окрестности такой точки, совпадают.
Совершенно аналогично в точке N ( ), в которой Q (g(у1
), y1
) = 0, а Р(g(у1
), y1
) ), в которой Q (g(у1
), y1
) = 0, а Р(g(у1
), y1
)  0, естественно «продолжением» интегральной кривой уравнения (II*) считать проходящую через эту точку интегральную кривую уравнения (II). 0, естественно «продолжением» интегральной кривой уравнения (II*) считать проходящую через эту точку интегральную кривую уравнения (II).
Нетрудно убедиться в том, что множество точек, состоящее из точек интегральной кривой уравнения (II). проходящей через некоторую, отличную от состояния равновесия системы (I) точку М0
(х0
, у0
) области Gи всех «продолжений» этой интегральной кривой в указанном выше смысле, совпадает с траекторией, проходящей через точку М0
.
Таким образом, одновременное задание уравнений (II) и (II*) определяет все траектории системы (I), отличные от состояний равновесия. Но в то время, как при рассмотрении системы (I) траектории определяются с помощью параметрических уравнении, при рассмотрении уравнений (II) и (II*) траектории определяются уравнениями в переменных х и у (уравнениями в декартовых координатах). В дальнейшем, рассматривая одновременно дифференциальные уравнения (II) и (II*), мы не будем выписывать оба эти уравнения: выписывая одно из этих уравнений, мы будем подразумевать, что рассматриваются оба. Мы будем также пользоваться следующими симметричными относительно х и у записями уравнений (II) и (II*), именно

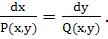 (III) (III)
Траектории системы (I), отличные от состояния равновесия, мы будем называть интегральными кривыми уравнения (III) (а также, не совсем точно, интегральными кривыми уравнения (II) или (II*)).
Точки, в которых одновременно
Р(х, у) = 0 и Q(x, у) = 0
и оба уравнения (II) и (II*) теряют смысл, называются особыми точками уравнений (II), (II*) или (III). Таким образом, состояниям равновесия системы (I) соответствуют особые точки уравнении (II), (II*) или (III) и, наоборот, особым точкам — состояния равновесия.
В то время, как система (I) определяет в области Gфазовой плоскости векторное поле, состоящее из векторов 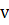 (х, у) с компонентами Р (х, у), Q (х, у) , уравнение (III) (или пара уравнений (II) и (II*)) определяет поле направлений или поле линейных элементов. Линейным элементом называется точка М и проходящий через эту точку ненаправленный прямолинейный отрезок, для которого М является внутренней точкой. Поле линейных элементов, определенное уравнением (III), получается, если через каждую точку М (х, у) области провести прямолинейный отрезок, имеющий угловой коэффициент (х, у) с компонентами Р (х, у), Q (х, у) , уравнение (III) (или пара уравнений (II) и (II*)) определяет поле направлений или поле линейных элементов. Линейным элементом называется точка М и проходящий через эту точку ненаправленный прямолинейный отрезок, для которого М является внутренней точкой. Поле линейных элементов, определенное уравнением (III), получается, если через каждую точку М (х, у) области провести прямолинейный отрезок, имеющий угловой коэффициент  (если (если  0, то соответствующий отрезок параллелен оси у). 0, то соответствующий отрезок параллелен оси у).
Очевидно, линейный элемент, соответствующий точке М (х, у), лежит на касательной к траектории, проходящей через точку М.
Если функция класса 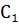 f (x, у) не обращается в нуль в области G, то системе f (x, у) не обращается в нуль в области G, то системе
 , , 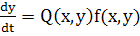 (I*) (I*)
соответствует, очевидно, то же дифференциальное уравнение (II)
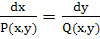 , что и системе , что и системе  , , 
Отсюда вторично вытекает доказанное в п. 7 утверждение, что системы (I) и (I*) имеют одни и те же траектории. Если функция f(х, у) обращается в нуль в точках области G, то, рассматривая уравнение

мы, очевидно, «теряем» особые точки системы (I*) (неявляющиеся состояниями равновесия системы (I)), для которых f(х,y) = 0.
12. Изоклины
Кривые, расположенные в области Gи имеющие уравнение
Q(x, у)  С С 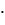 Р (х, у) = 0(34) Р (х, у) = 0(34)
(С — постоянное) или уравнение
Р(x, y) = 0,(35)
называются изоклинами (линиями равного наклона) системы (I) или уравнения (III). Эти кривые обладают, очевидно, тем свойством, что траектории системы (I), проходящие через все отличные от состояний равновесия точки каждой кривой, имеют в этих точках одинаковые направления касательных. Именно, угловые коэффициенты траекторий в точках изоклины (34) равны С, а в точках изоклины (35) равны  . Таким образом, направление касательной к траектории меняется только при переходе точки с одной изоклины на другую. . Таким образом, направление касательной к траектории меняется только при переходе точки с одной изоклины на другую.
Изоклины Q (х, у) = О и Р (х, у) = 0 называются главными изоклинами. В точках первой из них касательные к траекториям горизонтальны, а в точках второй — вертикальны. Поэтому главные изоклины называют также изоклинами горизонтальных, соответственно вертикальных, наклонов.
Очевидно, все состояния равновесия лежат на каждой из изоклин и, обратно, общие точки любых двух изоклин (различных) являются состояниями равновесия системы. В частности, состояния равновесия являются общими точками двух главных изоклин.
13. Понятия «интеграл», «интегральная кривая», «общий интеграл». использующиеся в классической литературе при рассмотрении аналитических систем
В этом пункте мы введем понятия «интеграл», «интегральная кривая», «общий интеграл» дифференциального уравнения или системы уравнений так, как это обычно делается в классической литературе при рассмотрении аналитических дифференциальных уравнений и систем.
Мы останавливаемся здесь на указанных понятиях, не играющих роли в излагаемой дальше теории ввиду того, что они часто используются в дальнейшем при рассмотрении примеров.
Пусть рассматриваемая система (I)
 Р(х, у) Р(х, у)  Q(x, у) Q(x, у)
является аналитической в области G. Соответствующее этой системе дифференциальное уравнение запишем в симметричной форме (III)

интеграл динамический плоскость траектория
Пусть функция F (х, у) удовлетворяет следующим условиям:
а) она является аналитической во всех точках кривой, заданной соотношением
F(x,y) = 0,(36)
б) во всех точках кривой (36) тождественно выполняется равенство
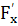 (х, у) Р(х, y) + (х, у) Р(х, y) + 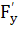 (x, y)Q(x, y)=0.(37) (x, y)Q(x, y)=0.(37)
Тогда соотношение (36) называется интегралом или частным интегралом уравнения (III) или системы (I), а кривая, определяемая этим соотношением, интегральной кривой уравнения (III) или системы (I).
Пусть F (х, у) = 0 — интеграл системы (I). Рассмотрим соответствующую интегральную кривую. Эта кривая может иметь в числе своих точек состояния равновесия системы (I), а также точки, в которых одновременно F'x
(х, у) = F'y
(х, у) = 0, т. е. особые точки кривой (36).
Покажем, что всякий “кусок” интегральной кривой, не содержащий состояний равновесия системы (I) и не имеющий особых точек, является траекторией системы (I) или представляет часть такой траектории.
В самом деле, рассмотрим произвольную точку М0
(х0
, ус
) такого куска кривой (36). Предположим, что в этой точке
F'y
(x0
, у0
)  0 0
Тогда в некоторой окрестности точки М0
кривая может быть задана уравнением вида y = f(x), причём
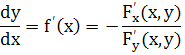
для всех точек кривой в этой окрестности. Так как F'y
(х0
, у0
)  0, то в окрестности точки М0
, F'y
(x, у) также отлична от нуля. Из соотношения (37) 0, то в окрестности точки М0
, F'y
(x, у) также отлична от нуля. Из соотношения (37)
F'x
(x, y)P(x, y) + F'y
(x, y)Q(x,y)=0
следует, что Р (х, у)  0 в окрестности точки М0
и что 0 в окрестности точки М0
и что

Но это значит, что функция y = f(x) удовлетворяет уравнению (II)
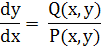
Аналогично рассматривается случай, когда F'x
(x0
, у0
)  0. Таким образом, рассматриваемый кусок кривой (36) является куском интегральной кривой в смысле п. 11, т. е. представляет траекторию или часть траектории системы (I). 0. Таким образом, рассматриваемый кусок кривой (36) является куском интегральной кривой в смысле п. 11, т. е. представляет траекторию или часть траектории системы (I).
Рассмотрим теперь семейство кривых
F{x%
у, С) = 0,(38)
определенное для значений С в некоторой области (обычно в некотором интервале).Соотношение (38) называется общим интегралом уравнения (III) или системы (1), если каждая кривая семейства (38) является интегральной кривой в определенном выше смысле и если каждая точка области G принадлежит по крайней мере одной из кривых (38).
Из этого определения следует, в частности, что если некоторая функция Ф (х, у) определена в области Gи является аналитической во всех точках этой области, за исключением, быть может, состояний равновесия системы (I), и удовлетворяет в области тождеству
Ф'х
(х, у)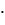 Р(х, у) + Ф'y
(х, y) Р(х, у) + Ф'y
(х, y)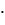 Q(x, y) Q(x, y) 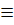 0, то соотношение 0, то соотношение
Ф(x, y) = С(39)
является общим интегралом системы (I).
Если у системы (I) (или уравнения (III) существует общий интеграл вида (39), причем Ф (x, у) есть функция, аналитическая во всех точках области G, то, говорят, что система (I) (или уравнение (III)) имеет в области G аналитический интеграл . В частности, системами вида (I), имеющими аналитический интеграл, являются так называемые гамильтоновы системы, о которых уже говорилось во введении

где Н (x, у) — аналитическая функция. H (х, у) = С является аналитическим интегралом (так называемым «интегралом энергии») этой системы.
Знание аналитического интеграла системы (I) в некоторых частных случаях помогает проводить качественное исследование системы (I).
14. Примеры
Мы приведем здесь ряд простых примеров динамических систем, поясняющих материал, изложенный в предыдущих пунктах.
Во всех указанных примерах динамические системы определены на всей плоскости. Приведем сначала два простейших примера динамических систем без состояний равновесия.
Пример 1.

Траектории — прямые, параллельные оси х

Состояний равновесия, очевидно, нет, все траектории (совпадающие с интегральными кривыми) являются целыми траекториями.
Пример 2.

 . .
Состояний равновесия нет, траектории не являются «целыми траекториями» ввиду того, что точки па этих траекториях уходят в бесконечность при t, стремящемся к конечному значению. Именно
 при t+ c1 при t+ c1
 (2k+ 1). (2k+ 1).
Пример 3
 (40) (40)
где a1
и a2
имеют одинаковые знаки.
На плоскости (х, у) (т. е. на фазовой плоскости системы (40)) эта система задает векторное поле, примерно изображенное на рис. 8, а при a1
< 0, а2
< 0 и на рис. 8, б при а1
> 0, а2
> 0. Прямые на этом рисунке являются изоклинами.
Система (40), очевидно, имеет единственное состояние равновесия О (0, 0). Решая систему (40) как линейную с постоянными коэффициентами, легко видеть, что решение, соответствующее начальным значениям t0
, x0
, у0
, имеет вид
 (41) (41)
Очевидно, в согласии с леммой 3 это решение является функцией t—t0
.
Траектории системы (40) проще всего получить, исключая tв уравнениях (41), т. е. переходя к декартовым координатам. Мы получаем

Полагая при уо
 0 0  , получим «параболы» , получим «параболы»
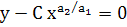 (42) (42)
а при у0
= 0 x=0 (43)
Из (42) при С = 0 мы получаем у =0 .
Нетрудно видеть, что если перейти от системы (40) к одному уравнению, например, записанному в виде
 или в виде или в виде 
и проинтегрировать его, то в качестве интегральных кривых в смысле п. 13 мы получим «параболы» (42) и две оси координат.

а) b)
Рис. 8
Отметим здесь же, что, как было указано в п. 13, уравнение (44) задает поле линейных элементов: оно представлено на рис. 9.
Траекториями системы (40) являются те части (половины) парабол (42) и координатных осей х = 0 и у = 0, на которые эти кривые разбиваются состоянием равновесия О (0, 0). Из соотношений (41) видно, что если a1
< 0, а2
<Z0, то точка на любой, отличной от О траектории, стремится к состоянию равновесия О при t , а если a1
> 0, a2
> 0, то при t , а если a1
> 0, a2
> 0, то при t . Мы будем сокращенно говорить, что траектория стремится к состоянию равновесия О соответственно при t . Мы будем сокращенно говорить, что траектория стремится к состоянию равновесия О соответственно при t или t или t . .

Рис. 9
Напоминаем, что когда «изображающая» точка, двигаясь по отличной от состояния равновесия траектории, стремится к некоторому состоянию равновесия А (х0
, у0
), то при этом |t|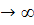 . Действительно, как это уже указывалось в п. 6, если бы tстремилось к конечному значению . Действительно, как это уже указывалось в п. 6, если бы tстремилось к конечному значению  , то это означало бы, что через точку пространства (х, у, t) с координатами , то это означало бы, что через точку пространства (х, у, t) с координатами  , х0
, у0
проходят две интегральные кривые: одна — прямая, параллельная оси t, соответствующая состоянию равновесия А (х0
, у0
), и другая, соответствующая траектории L. Это, очевидно, противоречит теореме о существовании и единственности решения. , х0
, у0
проходят две интегральные кривые: одна — прямая, параллельная оси t, соответствующая состоянию равновесия А (х0
, у0
), и другая, соответствующая траектории L. Это, очевидно, противоречит теореме о существовании и единственности решения.
Таким образом, разбиение на траектории, определенное системой (40) (с указанными на траекториях направлениями *)[ Если особых линий нет, то для того, чтобы наметить направление на траекториях, достаточно наметить направление в какой-либо одной точке, тогда во всех других точках направление определяется из соображений непрерывности. Определить же направление в какой-либо точке х0
, у0
, в которой Р (х0
, у0
) =/= 0, можно, вычисляя в этой точке Р (х0
, у0
) и определяя в этой точке знак Р (х0
, у0
); если Р (х0
, у0
) >(), то в точке (х0
, yQ
) dx/dt> 0, а значит, вблизи этой точки при движении по траектории в сторону возрастания txвозрастает, что н определяет направлении на траектории, проходящей через точку (а;0
, у0
). Совершенно аналогично можно наметить направления на траекториях, рассматривая знак dyidtв точке, в которой Q {х0
, у0
) М 0. 2)]), имеет вид, указанный на рис. 10. Состояние равновесия такого типа называется узлом,устойчивым в случае a1
< 0, a2
<0 (рис. 10, а) и неустойчивым в случае a1
>0, a2
>0 (рис.10,б).
Рассмотрим еще интерпретацию решений системы (40), т. е. интегральные кривые системы (40) в трехмерном пространстве ℝ3
с координатами х, у, t. Из формул (41) следует, что интегральными кривыми системы (40) в пространстве (х, у, t) являются

Рис. 10.
1) ось t, т. е. х = 0, у = 0 (эти уравнения получаются из уравнений (41) при х0
= у0
= 0); она проектируется в состояние равновесия О фазовой плоскости;
2) показательные кривые

расположенные в координатных полуплоскостях х > 0, у = 0 или х < 0, у = 0 и асимптотически стремящиеся к оси tпри  , если а1
< 0 (рис. 11, а), и при , если а1
< 0 (рис. 11, а), и при  , если а1
> 0; эти кривые проектируются в положительную и отрицательную полуоси абсцисс, являющиеся траекториями системы; , если а1
> 0; эти кривые проектируются в положительную и отрицательную полуоси абсцисс, являющиеся траекториями системы;
3)показательные кривые
х = 0, 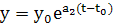
аналогичные кривым типа 2);
4) кривые
 (хо (хо
 0, уо 0, уо
 0), 0),
расположенные на параболических цилиндрах
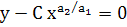 ,(С ,(С  0) 0)
с образующими параллельными оси t. Ось t разбивает каждый такой цилиндр на две «половины» и каждая интегральная кривая типа 4) лежит целиком в одной половине цилиндра и асимптотически стремится к оси tпри t , если a1
< 0, а2
< 0 (рис. 11, б), при , если a1
< 0, а2
< 0 (рис. 11, б), при  , если a1
> 0, a2
> 0.Интегральные кривые типа 4) получаются друг из друга сдвигом вдоль оси t. To же справедливо для интегральных кривых типа 2)или 3) , если a1
> 0, a2
> 0.Интегральные кривые типа 4) получаются друг из друга сдвигом вдоль оси t. To же справедливо для интегральных кривых типа 2)или 3)

а)б)
Рис.11
Пример 4
 (45) (45)
(а — отличная от нуля постоянная).
Векторное поле, определенное этой системой (при а<0), изображено на рис. 12.
Решая систему (45) как линейную систему с постоянными коэффициентами, мы получим решение, соответствующее начальным значениям t0
, х0
, у0
в следующем виде (оно, очевидно, является функцией t— t0
в согласии с леммой 3):
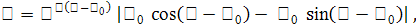 (46) (46)


Рис.12
Характер траекторий рассматриваемой системы удобнее исследовать, переходя к полярным координатам. Пусть 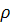 0
и 0
и  0
— полярные координаты точки М0
(х0
, у0
). Полагая х = 0
— полярные координаты точки М0
(х0
, у0
). Полагая х = 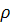 cos cos , у = , у = 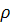 sin sin , нетрудно найти уравнение траекторий , нетрудно найти уравнение траекторий  = =  (t), (t), 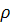 = = 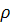 (t) в полярных координатах (здесь (t) в полярных координатах (здесь  (t), (t), 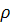 (t)—непрерывные функции от t, (t)—непрерывные функции от t,  (t) > 0, (t) > 0,  . . 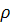 (t0
) = (t0
) = ). Мы получим после элементарных вычислений ). Мы получим после элементарных вычислений
 (47) (47)
Исключая t, получаем
 (48) (48)
Уравнение (48) дает, очевидно, все траектории системы (46). Если  эти траектории являются логарифмическими спиралями. При эти траектории являются логарифмическими спиралями. При  = 0 получается состояние равновесия О (0, 0). = 0 получается состояние равновесия О (0, 0).
Первое из двух уравнений (47) показывает, что все траектории стремятся к состоянию равновесия О при  , если а <0 (рис. 13, а), и при , если а <0 (рис. 13, а), и при  , если а > 0 (рис. 13, б). Состояние равновесия такого типа, как в данном примере, называется фокусом, устойчивым в случае а<0 и неустойчивым при a > 0. , если а > 0 (рис. 13, б). Состояние равновесия такого типа, как в данном примере, называется фокусом, устойчивым в случае а<0 и неустойчивым при a > 0.
Уравнение

соответствующее системе (45), является однородным. Интегрируя его с помощью подстановки  = и или = и или  = и, мы получим соотношение = и, мы получим соотношение
 (49) (49)
 (50) (50)
Первое из соотношений является общим интегралом системы (в смысле п. 13) во всякой области, не содержащей точек оси у (т. е. точек х = 0), а второе — во всякой области, не содержащей точек оси х. Однако, ни одно из этих соотношений не является в строгом смысле слова общим интегралом системы в области, содержащей точку О. «Целую» интегральную кривую, расположенную в такой области, можно получить, «склеивая» куски кривых (49) и (50).
Рассмотрим интерпретацию в трехмерном пространстве. Как и в предыдущем примере, ось tявляется интегральной кривой системы (45) в пространстве (х, у, t). Остальные интегральные кривые расположены на цилиндрических поверхностях, имеющих своими направляющими спирали (48), а образующими — прямые, параллельные оси t. Эти интегральные кривые асимптотически приближаются к оси tпри
t , если а < 0, и при t , если а < 0, и при t , если а > 0 , если а > 0
Отметим, что хотя формы траекторий в примерах 3 и 4 при a1
< 0, а2
< 0 и а < 0 (a1
> 0, а2
> 0 и а > 0) соответственно существенно отличаются, но в некотором смысле поведение траектории в том и в другом случае одинаково: именно, в обоих примерах все отличные от состояния равновесия траектории при t (или t (или t ) стремятся к состоянию равновесия. ) стремятся к состоянию равновесия.
 
а) б)
Рис. 13
Впоследствии, уточнив понятие «качественной структуры» разбиения на траектории, мы будем считать в примерах 3 и 4 «качественную структуру» разбиения на траектории одинаковой.
Пример 5
Эта система получается как частный случай системы (45) при а = 0. Решения, соответствующие начальным значениям t0
, x0
, у0
, имеют вид
х = х0
cos(t—t0
) —у0
sin(t—t0
) (52)
у= x0
sin (t —t0
) + y0
cos (t — t0
).
Непосредственной проверкой (или используя (52)) нетрудно убедиться, что является общим интегралом системы. Таким образом, в этом случае система имеет аналитический интеграл.
х2
+ у2
= С(53)
Траекториями системы, очевидно, являются состояние равновесия О (0, 0) и замкнутые траектории — концентрические окружности с центром в начале координат (рис. 14). Решения (52), соответствующие замкнутым траекториям — окружностям, являются периодическими функциями с периодом 2 . .

Рис. 14
Интегральными кривыми в трехмерном пространстве (x, у, t) являются ось tи винтовые линии, расположенные на круглых цилиндрах с направляющими (53). Шаг каждой винтовой линии равен 2 (рис. 15). (рис. 15).
Пример 6

Рис. 15
Векторное поле изображено на рис. 16.
Решение системы, соответствующее начальным значениям t0
, х0
, у0
, имеет вид
 (55) (55)
Точка О(0, 0) — состояние равновесия. Система имеет аналитический интеграл
ху = С.(56)
Интегральными кривыми при С  0 являются гиперболы (56) и при С = 0 — координатные оси х = 0 и у =0. Каждая гипербола состоит из двух траекторий (ее ветвей) и каждая из координатных осей — из трех траекторий (состояния равновесия О и двух полуосей). Соответствующее разбиение на траектории указано на рис. 17. 0 являются гиперболы (56) и при С = 0 — координатные оси х = 0 и у =0. Каждая гипербола состоит из двух траекторий (ее ветвей) и каждая из координатных осей — из трех траекторий (состояния равновесия О и двух полуосей). Соответствующее разбиение на траектории указано на рис. 17.
Из выражений (55) очевидно, что траектории, являющиеся полупрямыми оси х (получающаяся из (55) при у0
=0), стремятся к состоянию равновесия при t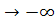 , а траектории, являющиеся полупрямыми оси у, при t , а траектории, являющиеся полупрямыми оси у, при t . Других траекторий, стремящихся к состоянию равновесия О, система не имеет. . Других траекторий, стремящихся к состоянию равновесия О, система не имеет.
Состояние равновесия такого типа, как у данной системы, называется седлом. Траектории, стремящиеся к седлу О, в данном случае полупрямые х =- 0 и у = 0 — называются сепаратрисами седла.
Траектории, сколь угодно близкие к сепаратрисе седла, при неограниченном возрастании tудаляются от сепаратрис. Такое поведение траекторий, очевидно, ни в какой мере не противоречит теореме 4 (о непрерывной зависимости от начальных значений), так как эта теорема рассматривает поведение близких траекторий только на конечном промежутке значений t. Нетрудно убедиться в том, что если взять за исходную траекторию сепаратрису, то для любого конечного промежутка значений tтеорема 4, очевидно, выполняется. Но при увеличении рассматриваемого промежутка величину б (см. теорему 4') нужно брать все меньше и меньше. Рассмотрение интегральных кривых системы (54) в пространстве (х, у, t) аналогично проведенному в предыдущих примерах, и мы его опускаем.
Рассмотрим теперь несколько более сложных примеров, именно, несколько примеров нелинейных динамических систем. При этом будем рассматривать только разбиение на траектории фазовой плоскости, заданное этими системами, не обращаясь уже больше к пространству (х, у, t), как в примерах линейных систем.

Рис. 16. Рис. 17

Рис. 18
Сделаем предварительно следующее элементарное замечание, являющееся, однако, весьма существенным для понимания некоторых основных свойств разбиения на траектории: в окрестности всякой точки, отличной от состояния равновесия в «малом», траектории ведут себя «аналогично параллельным прямым». Это наглядно иллюстрируется рис. 18. Далее, сделаем еще одно предварительное замечание. Пусть наряду с системо
 Р(х, у), Р(х, у), = Q(x, у) (l) = Q(x, у) (l)
задана система
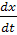 = (х, y) = (х, y) f(x, y)Q(x, у), f(x, y)Q(x, у),
 Q(x, y) Q(x, y) f(x, y)P(x, y), ( f(x, y)P(x, y), ( ) )
где f(x, y) — функция класса СN
, или аналитическая, определенная в той же области, что и система (I).
Легко видеть, что состояния равновесия системы (I) совпадают с состояниями равновесия системы ( ). В каждой точке области Gрассмотрим векторы ). В каждой точке области Gрассмотрим векторы  и и  , определенные соответственно системой (I) и ( , определенные соответственно системой (I) и ( ). Если обозначить через ). Если обозначить через  и и  углы между положительным направлением оси х и векторами углы между положительным направлением оси х и векторами  и и  , соответственно, то, очевидно , соответственно, то, очевидно

Тогда тангенс угла между вектором  и вектором и вектором  дается выражением. дается выражением.
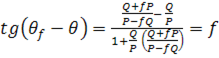 (57) (57)
Отметим, что в любой неособой точке области Gскалярное произведение
( ) = P2
+ Q2
> 0 ) = P2
+ Q2
> 0
Следовательно, векторы  и и  не перпендикулярны. не перпендикулярны.
Формулы (57) означают, как мы будем сокращенно говорить, что векторное поле системы ( ) повернуто по отношению к векторному полю системы (I) на острый угол, тангенс которого равен f. ) повернуто по отношению к векторному полю системы (I) на острый угол, тангенс которого равен f.
Пример 7
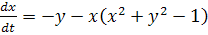 (58) (58)

Легко видеть, что система (58) имеет вид системы ( ), в которой Р (х, у) = — у, Q (х, у)=х и f(х, у) = х2
+ у2
— 1. Системой же ), в которой Р (х, у) = — у, Q (х, у)=х и f(х, у) = х2
+ у2
— 1. Системой же
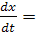 Р (х, у), Р (х, у),  = Q(x, у) = Q(x, у)
является система (51) примера 5. Отсюда следует, что система (58), так же как и (51), имеет единственное состояние равновесия О (0, 0) и что векторное поле системы (58) повернуто по отношению к нyлю системы (51) на острый угол, тангенс которого равен
х2
+у2
— 1
Этот угол, очевидно, положителен в точке, где
(x2
+ у2
— 1) > 0, и отрицателен,
где (х2
+ у2
— 1) < 0, и равен нулю на окружности х2
+ у2
— 1 = 0.
Учитывая знак выражения х2
+ у2
— 1, нетрудно убедиться в том, что при С > 1 траектории системы (58) входят внутрь окружностей х2
+ у2
= С и выходят из таких окружностей при С < 1. На рис. 19 показаны направления векторов поля системы (58) (нарисованные векторы имеют одинаковую длину и этим отличаются от векторов системы (58)).
Непосредственной проверкой легко убедиться, что окружность
х2
+ у2
— 1=0
есть интегральная кривая системы (58) и, следовательно, является ее замкнутой траекторией. В силу установленной выше связи между векторными полями систем (51) и (58) траектории
х2
+ у2
= С(59)
системы (51) являются циклами без контакта для траекторий системы (58), т. е. траектории системы (58) при С  1 ни в одной точке не касаются окружностей (59). Окружность жex2
+y2
= lявляется одновременно траекторией обеих систем (51), (58). 1 ни в одной точке не касаются окружностей (59). Окружность жex2
+y2
= lявляется одновременно траекторией обеих систем (51), (58).
На основании всего вышеизложенного представляется геометрически очевидным, что траектории системы (58) имеют характер, представленный на рис. 20. Строго можно доказать это найдя уравнения траекторий в полярных координатах. Полагая
 или или 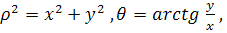
мы найдём
 , (60) , (60)

и  (61) (61)
 
Рис. 19. Рис. 20
Интегрируя последнее уравнение, мы получим

Это и есть уравнение траекторий в полярных координатах. Траектории, проходящей через точку М0
(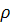 0
, 0
,  0
), соответствует значение 0
), соответствует значение
С = 
Если
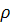 0
>1, то С > 0 и 0
>1, то С > 0 и 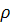 >1; >1; 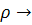 1 при 1 при  и и  при при 
(Очевидно, при этом  изменяется в интервале изменяется в интервале
 .) .) 
является решением уравнения (61). Если 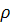 0
<1, toС<0 и 0
<1, toС<0 и 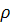 < 1. Тогда < 1. Тогда
 при при  и и 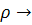 1 при 1 при 
Отсюда следует, что траектории системы имеют вид, указанный на рис. 20. Второе из уравнений (60) показывает, что если траектория проходит через точку
М0
(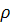 0
, 0
,  0
) 0
)
при t= t0
, то  = t + ( = t + ( 0
— t0
) 0
— t0
)
Состояние равновесия О (0, 0) так же, как и в случае линейной системы (45) примера 4, является фокусом, причем неустойчивым.
Траектория х2
+ у2
— 1 = 0 (в отличие от того, что было в примере 6) не окружена замкнутыми траекториями. Она сама является изолированной замкнутой траекторией, и все траектории, проходящие через точки достаточно малой ее окрестности, стремятся к ней при t . Такая замкнутая траектория называется предельным циклом. . Такая замкнутая траектория называется предельным циклом.

Подчеркнем, что на каждой траектории, лежащей вне предельного цикла, tизменяется от конечного значения
 до + до + 
Это можно выразить, сказав, что при убывании tточка на такой траектории уходит на бесконечность в конечное время. Таким образом, траектории, лежащие вне предельного цикла, не являются целыми. Напротив, все траектории, лежащие внутри предельного цикла, очевидно, являются целыми, т. е. tна них меняется от  до до  . Направление на траекториях может быть установлено непосредственно из системы. . Направление на траекториях может быть установлено непосредственно из системы.
Так, например, при х = 0 и у > 0 мы имеем 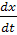 < 0, т. е. в точках оси у с возрастанием t < 0, т. е. в точках оси у с возрастанием t х убывает. Этого, очевидно, достаточно для определения направления на всех траекториях рассматриваемой системы. х убывает. Этого, очевидно, достаточно для определения направления на всех траекториях рассматриваемой системы.
Пример8
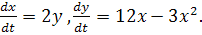 (62) (62)
Система имеет два состояния равновесия О(0, 0) и А (4, 0). Система, очевидно, имеет аналитический интеграл
 — 6x2 — 6x2
 x3
= C. (63) x3
= C. (63)
Характер семейства кривых (63) нетрудно установить, рассматривая вспомогательное семейство кривых:
и = 6х2
— х3
+ С.(64)
Так как у =  , то семейство кривых (64) имеет вид, представленный на рис. 21. a, а семейство кривых (63) — вид, представленный на рис. 21, б. Состояние равновесия О (О, 0) лежит на интегральной кривой (63) при С = 0. Эта интегральная кривая состоит из четырех траектории состояния равновесия О, двух незамкнутых траекторий, одна из которых стремится к О при t , то семейство кривых (64) имеет вид, представленный на рис. 21. a, а семейство кривых (63) — вид, представленный на рис. 21, б. Состояние равновесия О (О, 0) лежит на интегральной кривой (63) при С = 0. Эта интегральная кривая состоит из четырех траектории состояния равновесия О, двух незамкнутых траекторий, одна из которых стремится к О при t , а другая при t , а другая при t и «петли», стремящейся к состоянию равновесия О как при t и «петли», стремящейся к состоянию равновесия О как при t , так и при t , так и при t . .
Нетрудно убедиться в том, что состояние равновесия А (4, 0) принадлежит кривой (63), соответствующей С = —32. Эта кривая состоит из одной ветви и изолированной точки-состояния равновесия А. Остальные интегральные кривые не содержат состояний равновесия. При С < —32 кривая (63) имеет одну ветвь, расположенную левее бесконечных ветвей кривой (63) при С = 0. Если —32 < С < 0, то соответствующая кривая (63) состоит из двух ветвей, одна из которых есть замкнутая кривая (овал), содержащая точку А внутри себя. Наконец, при С > 0 кривая состоит из одной ветви (расположенной справа от кривой (63) при С = 0). Каждая ветвь интегральной кривой (при С  0) является траекторией. 0) является траекторией.
Состояние равновесия А является центром (см. пример 5). Состояние равновесия О — седло, стремящиеся к нему при t или t или t траектории — сепаратрисы седла (см. пример 6). траектории — сепаратрисы седла (см. пример 6).
Заметим, что сепаратрисой седла называется не траектория, а полутраектория. При этом, говоря о сепаратрисах, стремящихся к седлу, мы не считаем различными сепаратрисы, из которых одна является частью другой (например, С1
0 и С2
0 на рис. 22). С этой точки зрения в рассматриваемом примере к седлу стремится 4 сепаратрисы. Две из этих сепаратрис принадлежат одной и той же траектории —«петле».
Направление на траекториях может быть установлено, если, например, в первом уравнении (62) положить х = 0, у > 0. Мы получаем

что позволяет определить направление на траекториях (рис. 21, б).
Пример 9
 (65) (65)
Поле системы (65) может быть получено, если поле системы (62) повернуть на постоянный угол  такой, что tg такой, что tg = а. Следовательно, траектории системы (65) ни в одной точке не касаются траекторий системы (62). В частности, замкнутые траектории системы (62) являются циклами без контакта для траекторий системы (65). = а. Следовательно, траектории системы (65) ни в одной точке не касаются траекторий системы (62). В частности, замкнутые траектории системы (62) являются циклами без контакта для траекторий системы (65).
Для определенности предположим, что угол  < 0. Тогда всякая траектория системы (65), пересекающая при t= t0
какую-нибудь замкнутую траекторию системы (62) при t < 0. Тогда всякая траектория системы (65), пересекающая при t= t0
какую-нибудь замкнутую траекторию системы (62) при t , стремится к состоянию равновесия (А), а при возрастании tвыходит из области, заполненной замкнутыми траекториями. , стремится к состоянию равновесия (А), а при возрастании tвыходит из области, заполненной замкнутыми траекториями.
Состояние равновесия О (0, 0) системы (65) является так же, как у системы (62), седлом. Однако расположение сепаратрис седла у системы (65) (рис. 22) отличается от расположения сепаратрис системы (62).
И можно сказать, что сепаратриса системы (62) после поворота поля, т. е. после перехода к системе (64), «разделяется» на две сепаратрисы.
Сепаратрисы Lсистемы (65), лежащие слева от оси у, расположены аналогично сепаратрисам системы (62).
Пример 10
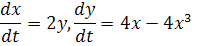
Приравнивая нулю правые части, мы находим состояния равновесия системы
О (0, 0), F1
(—1, 0), F2
(1, 0)
Легко убедиться, что
 (67) (67)
есть общий аналитический интеграл системы (66).
Исследование системы кривых ((57) легко провести полностью аналогично тому, как это было сделано в примере 8. Пользуясь вспомогательным семейством кривых
 , (68) , (68)
нетрудно построить семейство кривых (67) (рис. 23). Интегральная кривая
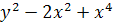
состоит из трех траектории — двух петель nсостояния равновесия 0(0, 0). При С > 0 каждая кривая (67) представляет собой одну замкнутую кривую (овал), при С < 0 — два овала. Каждый из овалов является траекторией. При С = 1 мы получаем две изолированные точки — состояния равновесия F1
и F2
. 1 мы получаем две изолированные точки — состояния равновесия F1
и F2
.
Состояние равновесия О седло, состояния равновесии F1
и F2
— центры. седло, состояния равновесии F1
и F2
— центры.

Рис. 22 Pис. 23
Пример. 11
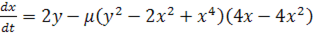 (69) (69)

Легко видеть, что векторное поле системы (69) повернуто но отношению к векторному полю системы (66) примера 10 на острый угол, тангенс которого равен 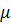 ( ( — 2х2 — 2х2
 х4
). Далее, непосредственно проверяется, что соотношение х4
). Далее, непосредственно проверяется, что соотношение
( — 2х2 — 2х2
 х4
) = 0(70) х4
) = 0(70)
является интегралом системы (69). Поэтому кривая (70), представляющая интегральную кривую системы (66), является также интегральной кривой системы (69).
Наконец, заметим, что внутри кривой (70) выражение  — 2х2 — 2х2
 х4
меньше 0, а вне — больше нуля. Сравнивая векторные поля систем (66) и (69), нетрудно видеть, что все замкнутые траектории системы (66) (рис. 23) являются циклами без контакта для траекторий системы (69). х4
меньше 0, а вне — больше нуля. Сравнивая векторные поля систем (66) и (69), нетрудно видеть, что все замкнутые траектории системы (66) (рис. 23) являются циклами без контакта для траекторий системы (69).
На основании этого, можно показать, что разбиение на траектории имеет вид, представленный на рис. 24. а,при 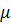 > 0 и на рис. 24.б при > 0 и на рис. 24.б при 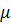 < 0.При < 0.При  > 0 все траектории, лежащие вне кривой (70) при tвозрастающем, уходят на бесконечность, а при t > 0 все траектории, лежащие вне кривой (70) при tвозрастающем, уходят на бесконечность, а при t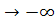 «накручиваются» на кривую (70). Траектории, лежащие внутри кривой (70) при t «накручиваются» на кривую (70). Траектории, лежащие внутри кривой (70) при t , «накручиваются» на однуиз простых замкнутых кривых, составляющих часть кривой (70), а при t , «накручиваются» на однуиз простых замкнутых кривых, составляющих часть кривой (70), а при t стремятся к одному из состояний равновесия F1
и F2
, которые являются «фокусами». стремятся к одному из состояний равновесия F1
и F2
, которые являются «фокусами».

Рис. 24.а. Рис. 24.6.
Состояние равновесия О — седло, кривая (70) является предельным континуумом для траекторий, расположенных вне нее, а каждая ее петля (вместе с состоянием равновесия О) — предельным континуумом для траекторий, расположенных внутри этой петли. Аналогично обстоит дело при
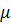 < 0 < 0
15. Выводы
Приведенные выше примеры, на которых был проиллюстрирован целый ряд установленных выше предложений, одновременно являются примерами «исчерпывающего» исследования «качественной структуры» разбиения на траектории, т. е. «исчерпывающего» качественного исследования динамической системы.
С точки зрения качественного исследования знание точной формы траектории не представляет интереса: мы уже подчеркивали это, указывая на одинаковое «качественное поведение» траекторий в случае узла и фокуса. Однако существенный интерес представляет, например, знание числа состояний равновесия, факт наличия или отсутствия изолированной замкнутой траектории — предельного цикла, ход сепаратрис и так далее.
В приведенных выше примерах «исчерпывающее» качественное исследование разбиения на траектории удалось провести ввиду простоты рассматриваемых динамических систем. В примерах 1—6 динамические системы являлись линейными. В других примерах получены обозримые аналитические выражения для решения или интегралов. Это позволяло полностью решить вопрос о характере разбиения на траектории. Исследование характера разбиения на траектории в примерах 9 и 11 было проведено, опираясь на результаты примеров 8 и 10, на понятие циклов и кривых без контактов и на свойства поворота поля.Конечно, такое элементарное и исчерпывающее качественное исследование, как правило, не удается провести в случае произвольной динамической системы вида (I).
Мы не можем рассчитывать получить элементарные выражения для решений или интегралов в случае произвольной динамической системы. Вследствие этого даже очень простые но виду динамические системы, имеющие интерес в прикладных вопросах, требуют для своего качественного исследования создания специальных приемов. Примером этому может служить «система Ван-дер-Поля»

качественному исследованию которой посвящено большое количество работ. Таким образом, естественно встает вопрос об отыскании регулярных методов качественного исследования динамических систем или хотя бы о достаточно эффективных приемах такого исследования.
Подчеркнем еще раз, что даже в тех случаях, когда у рассматриваемой динамической системы существует аналитический интеграл (в смысле п. 13) и найдено его аналитическое выражение
Ф(х, у) = С(71)
(как это имело место в примерах 8 и 9), вопрос качественного исследования разбиения на траектории, как правило, не делается тривиальным. Он сводится, правда, к вопросу качественного исследования семейства кривых (71). Однако в настоящее время не существует регулярных методов качественного исследования семейства кривых (71) или отдельной кривой
F(x, y) = 0
Такие методы отсутствуют даже в том случае, когда функции Ф (х, у) и F (х, у) являются многочленами.Поэтому ни в какой мере не следует думать, что знание аналитического интеграла (в тех случаях, когда он существует) сразу же решает задачу качественного исследования динамической системы: оно просто сводит одну задачу — задачу непосредственного исследования разбиения на траектории, заданного системой (I) — к задаче качественного исследования семейства кривых вида (71).Поэтому представляется целесообразным отыскание методов или приемов непосредственного качественного исследования системы (I), без предварительного нахождения аналитических выражений для решений. Прежде чем переходить к описанию таких приемов, естественно установить некоторые общие свойства разбиения на траектории. Необходимо выяснить: каким вообще может быть разбиение на траектории, определенное системой (I). Вопросом, который при этом возникает первым, является вопрос о том, какие типы траекторий вообще возможны у динамических систем вида (I). В п. 5 было установлено, что траектории могут быть состояниями равновесия, замкнутыми и незамкнутыми траекториями. Однако это еще слишком общие, неконкретные сведения о возможном характере траектории (в случае незамкнутой траектории).
|