| 5 |
2 |
3 |
1 |
6 |
4 |
8 |
9 |
5 |
7 |
| 4 |
7 |
8 |
2 |
9 |
10 |
4 |
5 |
3 |
2 |
| 9 |
7 |
8 |
6 |
5 |
4 |
3 |
5 |
2 |
1 |
| 2 |
3 |
4 |
1 |
5 |
6 |
7 |
5 |
3 |
10 |
1. Вычислить критерий хи-квадрат и сделать вывод о нормальности данного распределения.
2. Построить график эмпирического распределения.
Критерий Пирсона
1. Наблюдаемый критерий Пирсона вычисляется по следующей формуле:
критерий пирсон колмогоров распределение частота
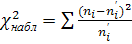 , ,
где 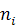 - наблюдаемая частота; - наблюдаемая частота; 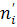 - теоретическая частота. - теоретическая частота.
Массив данных о значениях случайной величины X, как элементов выборки представим в таблице 1.1 в ячейках В2:К5
.
Таблица
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
| 1 |
| 2 |
5 |
2 |
3 |
1 |
6 |
4 |
8 |
9 |
5 |
7 |
| 3 |
4 |
7 |
8 |
2 |
9 |
10 |
4 |
5 |
3 |
2 |
| 4 |
9 |
7 |
8 |
6 |
5 |
4 |
3 |
5 |
2 |
1 |
| 5 |
2 |
3 |
4 |
1 |
5 |
6 |
7 |
5 |
3 |
10 |
| 6 |
| 7 |
n= |
40 |
k= |
6,31884 |
| 8 |
 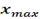 |
10 |
h= |
1,42431 |
| 9 |
1 |
2. Разобьем исходные данные по интервалам. Количество интервалов вычислим по формуле 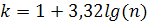 , где n – объем выборки. , где n – объем выборки.
Объем выборки определим с помощью функции СЧЕТ
. Для этого установим курсор в ячейку В7
, щелкнем мышкой над кнопкой  , которая находится на панели инструментов. Появится окно «Мастер функций – шаг 1 из 2»
, в котором в категории «Статистические»
выбираем функцию СЧЕТ.
Затем мышкой выполним команду ОК
. В появившемся окне «Аргументы функции»
поставим курсор в строку ввода «Значение 1»
и мышкой выделим массив В2:К5,
щелкнем мышкой ОК.
В ячейке В7
появится значение объема данных, число 40. , которая находится на панели инструментов. Появится окно «Мастер функций – шаг 1 из 2»
, в котором в категории «Статистические»
выбираем функцию СЧЕТ.
Затем мышкой выполним команду ОК
. В появившемся окне «Аргументы функции»
поставим курсор в строку ввода «Значение 1»
и мышкой выделим массив В2:К5,
щелкнем мышкой ОК.
В ячейке В7
появится значение объема данных, число 40.
Введем в ячейку Е7
формулу: =1+3,32*
Log
(В7)
,в ячейке Е7
появится число 6,31884.
Далее вычислим шаг интервалов, используя формулу 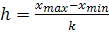 , где , где 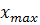 - максимальное значение варианты из массива данных; - максимальное значение варианты из массива данных; 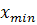 – минимальное значение варианты; k – количество интервалов. – минимальное значение варианты; k – количество интервалов.
Выделим пустую ячейку В8
и вызовем окно «Мастер функций – шаг 1 из 2»
, в котором инициируем функцию «МАКС»
, введем в строку ввода блок ячеек В2:К5.
В ячейке В8
появится максимальное значение данных, число 10.Выделим пустую ячейку В9
и вызовем окно «Мастер функций – шаг 1 из 2»
, в котором инициируем функцию «МИН»
, введем в строку ввода блок ячеек В2:К5.
В ячейке В9
появится максимальное значение данных, число 1.
Теперь введем в ячейку Е8
формулу: =(В8-В9)/Е7.
Получим значение шага h=1,42431. Округлим его, получаем h=1,5.
Таким образом, имеем шаг h=1,5, количество интервалов округлим до 7, k=7. Вычислим теоретические частоты по интервалам  . Для этого построим новую расчетную таблицу 1.2. Значения частот определяем с использованием функции ЧАСТОТА( )
. . Для этого построим новую расчетную таблицу 1.2. Значения частот определяем с использованием функции ЧАСТОТА( )
.
Введем в ячейку В11
заголовок для левого конца интервала  , в ячейку С11
– заголовок правого конца интервала , в ячейку С11
– заголовок правого конца интервала 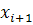 . Далее вводим значения в столбцы В12:В18
и С12:С18
. . Далее вводим значения в столбцы В12:В18
и С12:С18
.
Таблица
| A |
B |
C |
D |
E |
F |
G |
H |
I |
| 10 |
| 11 |
 |
 |
 |
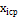 |
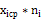 |
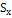 |
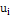 |
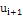 |
| 12 |
1 |
2,5 |
3 |
1,75 |
5,25 |
59,7417 |
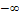 |
-1,4232 |
| 13 |
2,5 |
4 |
5 |
3,25 |
16,25 |
43,882 |
-1,4232 |
-0,8482 |
| 14 |
4 |
5,5 |
10 |
4,75 |
47,5 |
21,3891 |
-0,8482 |
-0,2731 |
| 15 |
5,5 |
7 |
7 |
6,25 |
43,75 |
0,00984 |
-0,2731 |
0,30188 |
| 16 |
7 |
8,5 |
7 |
7,75 |
54,25 |
16,5473 |
0,30188 |
0,8769 |
| 17 |
8,5 |
10 |
3 |
9,25 |
27,75 |
27,6792 |
0,8769 |
1,45192 |
| 18 |
10 |
11,5 |
5 |
10,75 |
53,75 |
102,945 |
1,45192 |
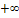 |
| 19 |
сумма |
40 |
248,5 |
272,194 |
| 20 |
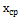 = = |
6,2125 |
6,80484 |
| 21 |
 |
2,60861 |
3. 1) Выделим мышкой пустой столбец D
12:
D
18.
Щелкнем мышкой над кнопкой  функцию ЧАСТОТА
. Появится окно «Аргументы и функции»
. Вводим в строку массив данных блок В2:К5.
Затем переводим курсор в строку массив интервалов. Т.е. выделяем столбец В12:В18
инажимаем последовательно на клавиатуре три кнопки Ctrl
+
Shift
+
Enter
. функцию ЧАСТОТА
. Появится окно «Аргументы и функции»
. Вводим в строку массив данных блок В2:К5.
Затем переводим курсор в строку массив интервалов. Т.е. выделяем столбец В12:В18
инажимаем последовательно на клавиатуре три кнопки Ctrl
+
Shift
+
Enter
.
2) Столбец Е12:Е18
заполним средними значениями каждого интервала. В столбцеF
12:
F
18
вычислим средние значения для всего массива данных . Для этого в ячейкуF
12
вводим формулу =
D
12*
E
12
и протягиваем мышкой значение этой ячейки до конца таблицы. В ячейке F
19
вычисляем сумму, а в ячейке F
20
–среднее значение по формуле =
F
19/
D
19.
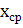 =
6,2125 =
6,2125
3) Вычисляем среднее квадратическое отклонение по формуле
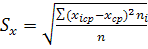 . .
Вводим с клавиатуры в ячейку G
12
формулу =(
E
12-59,875)^2*
D
12
и протягиваем ячейку до ячейки G
18.
Далее вычисляем в G
19
сумму, в ячейке G
20
– среднее значение, разделив сумму на 40 и в ячейке G
21
извлекаем корень квадратный по формуле =корень(
G
20).
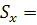 2,60861. 2,60861.
4. Вычислим безразмерные аргументы 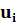 для левых концов интервала и для левых концов интервала и 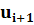 для правых концов интервала по формуле для правых концов интервала по формуле 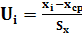 . .
В ячейку H
12
вводим формулу =(В12-6,2125)/ 2,60861
и протягиваем ее до конца столбца, т.е. заполняем нижние значения соответствующими вычислениями. Аналогично вычисляем величины 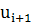 формулой: =(
C
12-6,2125)/ 2,60861. формулой: =(
C
12-6,2125)/ 2,60861.
Далее вычисляем значения функций Лапласа F
(
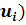 и F
( и F
(
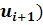 потаблице и результаты помещаем в новую расчетную таблицу 1.3 в ячейки В24:В30
и С24:С30. потаблице и результаты помещаем в новую расчетную таблицу 1.3 в ячейки В24:В30
и С24:С30.
Таблица 1.3
| A |
B |
C |
D |
E |
F |
| 22 |
| 23 |
F(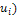 |
F(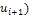 |
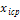 |
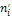 |
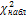 |
| 24 |
-0,5 |
-0,4222 |
1,75 |
3,112 |
0,00403 |
| 25 |
-0,4222 |
-0,2968 |
3,25 |
5,016 |
5,1E-05 |
| 26 |
-0,2968 |
-0,1064 |
4,75 |
7,616 |
0,74625 |
| 27 |
-0,1064 |
0,1179 |
6,25 |
8,972 |
0,43344 |
| 28 |
0,1179 |
0,315 |
7,75 |
7,884 |
0,09912 |
| 29 |
0,315 |
0,4265 |
9,25 |
4,46 |
0,47794 |
| 30 |
0,4265 |
0,5 |
10,75 |
2,94 |
1,4434 |
| 31 |
сумма |
40 |
3,20423 |
Вычисляем теоретические частоты по формуле 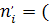 F( F(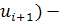 F( F(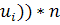 . Вводим в ячейку E
24
формулу =(С24-В24)*60
и протягиваем формулу до конца столбца. . Вводим в ячейку E
24
формулу =(С24-В24)*60
и протягиваем формулу до конца столбца.
Вычисляем критерий Пирсона Хи-квадрат. В ячейку F
24
вводим формулу: =(
D
12-
E
24)^2/
E
24.
В итоге, как видно из таблицы 1.3 получено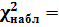 3,20423. 3,20423.
Сравним найденное значение с табличным по уровню значимости α=0,05 и степени свободы s=k-2=7-2=5. 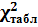 =11,1 =11,1
Т.о., наблюдаемый критерий меньше табличного, следовательно, исходные данные соответствуют нормальному закону распределения.
Критерий согласия Колмогорова - Смирнова
Вычислим критерий в по формуле 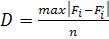 , где , где  – экспериментальные и теоретические накопленные частоты соответственно. Накопленные частоты получаются путем последовательного сложения частот по всем интервалам, начиная с первого. Для удобства вычислений составим расчетную таблицу 2.1. – экспериментальные и теоретические накопленные частоты соответственно. Накопленные частоты получаются путем последовательного сложения частот по всем интервалам, начиная с первого. Для удобства вычислений составим расчетную таблицу 2.1.
Таблица 2.1
| A |
B |
C |
D |
E |
F |
G |
H |
I |
| 32 |
| 33 |
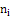 |
3 |
5 |
10 |
7 |
7 |
3 |
5 |
| 34 |
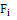 |
3 |
8 |
18 |
25 |
32 |
35 |
40 |
| 35 |
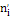 |
3,112 |
5,016 |
7,616 |
8,972 |
7,884 |
4,46 |
2,94 |
| 36 |
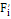 |
3,112 |
8,128 |
15,744 |
24,716 |
32,6 |
37,06 |
40 |
| 37 |
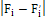 |
0,112 |
0,128 |
2,256 |
0,284 |
0,6 |
2,06 |
| 38 |
Dmax = |
2,256 |
Максимальное значение абсолютной разности накопленных частот равно 2,256. По формуле делим его на n=40 и получим D=0,0564. Найдем табличное значение критерия с уровнем значимости α=0,05 и степенью свободы n=40. 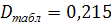 . .
Следовательно, исходные данные соответствуют нормальному распределению, т.к. 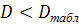 . .
Т.о., второй метод подтверждает наличие нормального распределения выборки.
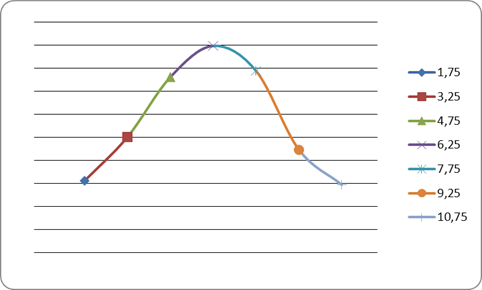
Построение графика распределения частот
Для построения графика распределения частот используем данные таблицы 1.3. В качестве абсциссы берем координаты 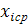 массив D
24:
D
30
. В качестве ординат – блок E
24:
E
30. массив D
24:
D
30
. В качестве ординат – блок E
24:
E
30.
1. Выполним команду ВСТАВКА
из верхнего меню. Выберем пиктограмму Точечная
и в появившемся окне вид плавной кривой с точками.
2. В верхней ленте выбрать команду Выбрать данные.
Появится окно Выбор исходных данных.
После чего выделяем столбец D
24:
D
30
нажимаем клавишу Ctrl
на клавиатуре и, опуская ее, выделяем столбец E
24:
E
30.
Щелкнем по команде ОК
. Появится изображение графика.
|