Кафедра: Высшая математика
Реферат
по дисциплине «Высшая математика»
Тема: «Предел и непрерывность функций нескольких переменных»
Тольятти, 2008
Введение
Понятие функции одной переменной не охватывает все зависимости, существующие в природе. Даже в самых простых задачах встречаются величины, значения которых определяются совокупностью значений нескольких величин.
Для изучения подобных зависимостей вводится понятие функции нескольких переменных.
Понятие функции нескольких переменных
Определение.
Величина u
называется функцией нескольких независимых переменных (x
,
y
,
z
, …,
t
), если каждой совокупности значений этих переменных ставится в соответствие определенное значение величины u
.
Если переменная является функцией от двух переменных х
и у
, то функциональную зависимость обозначают
z
=
f
(
x
,
y
).
Символ f
определяет здесь совокупность действий или правило для вычисления значения z
по данной паре значений х
и у
.
Так, для функции z
=
x
2
+ 3xy
при х
= 1 и у
= 1 имеем z
= 4,
при х
= 2 и у
= 3 имеем z
= 22,
при х
= 4 и у
= 0 имеем z
= 16 и т.д.
Аналогично называется величина u
функцией от трех переменных x
,
y
,
z
,
если дано правило, как по данной тройке значений x
,
y
иz
вычислить соответствующее значение u
:
u
=
F
(
x
,
y
,
z
).
Здесь символ F
определяет совокупность действий или правило для вычисления значения u
, соответствующего данным значениям x
,
y
иz
.
Так, для функции u
=
xy
+
2xz
–
3yz
при х
= 1, у
= 1 и z
= 1 имеем u
=
0,
при х
= 1, у
= -2 и z
= 3 имеем u
=
22,
при х
= 2, у
= -1 и z
= -2 имеем u
=
-16 и т.д.
Таким образом, если в силу некоторого закона каждой совокупности п
чисел (x
,
y
,
z
, …,
t
) из некоторого множества Е
ставится в соответствие определенное значение переменной u
, то и u
называется функцией от п
переменных x
,
y
,
z
, …,
t
, определенной на множестве Е
, и обозначается
u
=
f
(x
,
y
,
z
, …,
t
).
Переменные x
,
y
,
z
, …,
t
называются аргументами функции, множество Е
– областью определения функции.
Частным значением функции называется значение функции в некоторой точке М
0
(x
0
,
y
0
,
z
0
, …,
t
0
) и обозначается f
(М
0
) = f
(x
0
,
y
0
,
z
0
, …,
t
0
).
Областью определения функции называется множество всех значений аргументов, которым соответствуют какие-либо действительные значения функции.
Функция двух переменных z
=
f
(
x
,
y
)
в пространстве представляется некоторой поверхностью. То есть, когда точка с координатами х
, у
пробегает всю область определения функции, расположенную в плоскости хОу
, соответствующая пространственная точка, вообще говоря, описывает поверхность.
Функцию трех переменных u
=
F
(
x
,
y
,
z
)
рассматривают как функцию точки некоторого множества точек трехмерного пространства. Аналогично, функцию п
переменных u
=
f
(x
,
y
,
z
, …,
t
) рассматривают как функцию точки некоторого п
-мерного пространства.
Предел функции нескольких переменных
Для того чтобы дать понятие предела функции нескольких переменных, ограничимся случаем двух переменных х
и у
. По определению функция f
(
x
,
y
)
имеет предел в точке (х
0
, у
0
), равный числу А
, обозначаемый так:
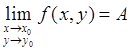 (1) (1)
(пишут еще f
(
x
,
y
)
→А
при (
x
,
y
)
→ (х
0
, у
0
)), если она определена в некоторой окрестности точки (х
0
, у
0
), за исключением, быть может, самой этой точки и если существует предел
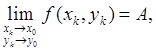 (2) (2)
какова бы ни была стремящаяся к (х
0
, у
0
) последовательность точек (xk
,
yk
).
Так же, как в случае функции одной переменной, можно ввести другое эквивалентное определение предела функции двух переменных: функция f
имеет в точке (х
0
, у
0
) предел, равный А
, если она определена в некоторой окрестности точки (х
0
, у
0
) за исключением, быть может, самой этой точки, и для любого ε > 0 найдется такое δ > 0, что
| f
(
x
,
y
)
– A
| < ε(3)
для всех (
x
,
y
)
, удовлетворяющих неравенствам
0 < 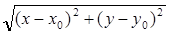 < δ. (4) < δ. (4)
Это определение, в свою очередь, эквивалентно следующему: для любого ε > 0 найдется δ-окрестность точки (х
0
, у
0
) такая, что для всех (x
,
y
) из этой окрестности, отличных от (х
0
, у
0
), выполняется неравенство (3).
Так как координаты произвольной точки (x
,
y
) окрестности точки (х
0
, у
0
) можно записать в виде х = х
0
+
Δх
, у = у
0
+ Δу
, то равенство (1) эквивалентно следующему равенству:
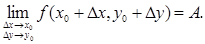
Рассмотрим некоторую функции, заданную в окрестности точки (х
0
, у
0
), кроме, быть может, самой этой точки.
Пусть ω = (ωх
, ωу
) – произвольный вектор длины единица (|ω|2
= ωх
2
+ ωу
2
= 1) и t
> 0 – скаляр. Точки вида
(х
0
+ t
ωх
, y
0
+ t
ωу
) (0 < t
)
образуют луч, выходящий из (х
0
, у
0
) в направлении вектора ω. Для каждого ω можно рассматривать функцию
f
(х
0
+ t
ωх
, y
0
+ t
ωу
) (0 < t
< δ)
от скалярной переменной t
, где δ – достаточно малое число.
Предел этой функции (одной переменной t
)
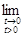 f
(х
0
+ t
ωх
, y
0
+ t
ωу
), f
(х
0
+ t
ωх
, y
0
+ t
ωу
),
если он существует, естественно называть пределом f
в точке (х
0
, у
0
) по направлению ω.
Пример 1.
Функции
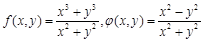
определены на плоскости (x
,
y
) за исключением точки х
0
= 0, у
0
= 0. Имеем (учесть, что 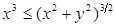 и и 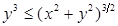 ): ):
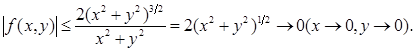
Отсюда
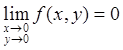
(для ε > 0 полагаем δ = ε/2 и тогда |f
(
x
,
y
)
| < ε, если 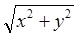 < δ). < δ).
Далее, считая, что k
– постоянная, имеем для y
=
kx
равенство
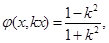
из которого видно, что предел φ в точке (0, 0) по разным направлениям вообще различен (единичный вектор луча y
=
kx
, х
> 0, имеет вид
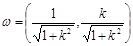 ). ).
Пример 2.
Рассмотрим в R
2
функцию
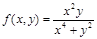 (х
4
+ у
2
≠ 0). (х
4
+ у
2
≠ 0).
Данная функция в точке (0, 0) на любой прямой y
=
kx
, проходящей через начало координат, имеет предел, равный нулю:
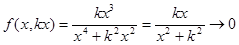 при х
→ 0. при х
→ 0.
Однако эта функция не имеет предела в точки (0, 0), ибо при у = х
2
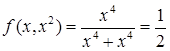 и и 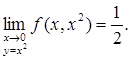
Будем писать 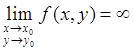 , если функция f
определена в некоторой окрестности точки (х
0
, у
0
), за исключением, быть может, самой точки (х
0
, у
0
) и для всякого N
> 0 найдется δ > 0 такое, что , если функция f
определена в некоторой окрестности точки (х
0
, у
0
), за исключением, быть может, самой точки (х
0
, у
0
) и для всякого N
> 0 найдется δ > 0 такое, что
|f
(
x
,
y
)
| > N
,
коль скоро 0 < 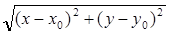 < δ. < δ.
Можно также говорить о пределе f
, когда х
, у
→ ∞:
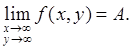 (5) (5)
Например, в случае конечного числа А
равенство (5) надо понимать в том смысле, что для всякого ε > 0 найдется такое N
> 0, что для всех х
, у
, для которых |x
| > N
, |y
| > N
, функция f
определена и имеет место неравенство
|f
(
x
,
y
)
– А
| < ε.
Справедливы равенства
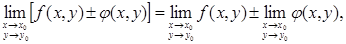 (6) (6)
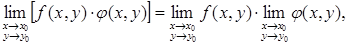 (7) (7)
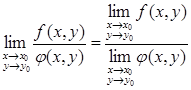 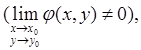 (8) (8)
где может быть х
→ ∞, у
→ ∞. При этом, как обычно, пределы (конечные) в их левых частях существуют, если существуют пределы f
и φ.
Докажем для примера (7).
Пусть (xk
,
yk
) → (х
0
, у
0
) ((xk
,
yk
) ≠ (х
0
, у
0
)); тогда
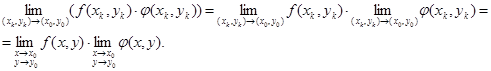 (9) (9)
Таким образом, предел в левой части (9) существует и равен правой части (9), а так как последовательность (xk
,
yk
) стремится к (х
0
, у
0
) по любому закону, то этот предел равен пределу функции f
(
x
,
y
)
∙φ (
x
,
y
)
в точке (х
0
, у
0
).
Теорема.
если функция f
(
x
,
y
)
имеет предел, не равный нулю в точке (х
0
, у
0
), т.е.
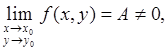
то существует δ > 0 такое, что для всех х
, у
, удовлетворяющих неравенствам
0 < 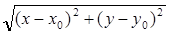 < δ, (10) < δ, (10)
она удовлетворяет неравенству
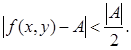 (12) (12)
Поэтому для таких (
x
,
y
)
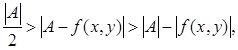
т.е. имеет место неравенство (11). Из неравенства (12) для указанных (
x
,
y
)
следует 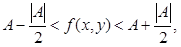 откуда откуда 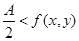 при A
> 0 и при A
> 0 и 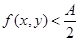 при при
A
< 0 (сохранение знака).
По определению функция f
(
x
) =
f
(
x
1
, …, xn
) =
A
имеет предел в точке
x
0
= 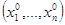 , равный числу А
, обозначаемый так: , равный числу А
, обозначаемый так:
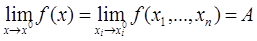
(пишут еще f
(
x
)
→ A
(x
→ x
0
)), если она определена на некоторой окрестности точки x
0
, за исключением, быть может, ее самой, и если существует предел
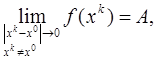
какова бы ни была стремящаяся к x
0
последовательность точек х
k
из указанной окрестности (k
= 1, 2, ...), отличных от x
0
.
Другое эквивалентное определение заключается в следующем: функция f
имеет в точке x
0
предел, равный А
, если она определена в некоторой окрестности точки x
0
, за исключением, быть может, ее самой, и для любого ε > 0 найдется такое δ > 0, что
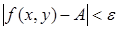 (13) (13)
для всех х
, удовлетворяющих неравенствам
0 < |x
–
x
0
| < δ.
Это определение в свою очередь эквивалентно следующему: для любого ε > 0 найдется окрестность U
(
x
0
)
точки x
0
такая, что для всех х
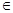 U
(
x
0
)
, х
≠ x
0
, выполняется неравенство (13). U
(
x
0
)
, х
≠ x
0
, выполняется неравенство (13).
Очевидно, что если число А
есть предел f
(
x
)
в x
0
, то А
есть предел функции f
(
x
0
+ h
)
от h
в нулевой точке:
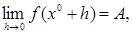
и наоборот.
Рассмотрим некоторую функцию f
, заданную во всех точках окрестности точки x
0
, кроме, быть может, точки x
0
; пусть ω = (ω1
, ..., ωп
) – произвольный вектор длины единица (|ω| = 1) и t
> 0 – скаляр. Точки вида x
0
+ t
ω (0 < t
) образуют выходящий из x
0
луч в направлении вектора ω. Для каждого ω можно рассматривать функцию
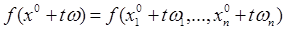 (0 < t
< δω
) (0 < t
< δω
)
от скалярной переменной t
, где δω
есть число, зависящее от ω. Предел этой функции (от одной переменной t
)
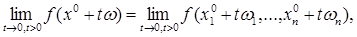
если он существует, естественно называть пределом f
в точке x
0
по направлению вектора ω.
Будем писать 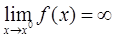 , если функция f
определена в некоторой окрестности x
0
, за исключением, быть может, x
0
, и для всякого N
> 0 найдется δ > 0 такое, что |f
(
x
)
| >N
, коль скоро 0 < |x
–
x
0
| < δ. , если функция f
определена в некоторой окрестности x
0
, за исключением, быть может, x
0
, и для всякого N
> 0 найдется δ > 0 такое, что |f
(
x
)
| >N
, коль скоро 0 < |x
–
x
0
| < δ.
Можно говорить о пределе f
, когда х
→ ∞:
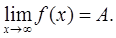 (14) (14)
Например, в случае конечного числа А
равенство (14) надо понимать в том смысле, что для всякого ε > 0 можно указать такое N
> 0, что для точек х
, для которых |x
| > N
, функция f
определена и имеет место неравенство 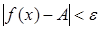 . .
Итак, предел функции f
(
x
)
= f
(
x
1
, ..., хп
)
от п
переменных определяется по аналогии так же, как для функции от двух переменных.
Таким образом, перейдем к определению предела функции нескольких переменных.
Число А
называется пределом функции f
(
M
)
при М
→ М
0
, если для любого числа ε > 0 всегда найдется такое число δ > 0, что для любых точек М
, отличных от М
0
и удовлетворяющих условию | ММ
0
| < δ, будет иметь место неравенство |f
(
M
)
– А
| < ε.
Предел обозначают 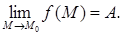 В случае функции двух переменных В случае функции двух переменных 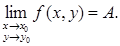
Теоремы о пределах.
Если функции f
1
(
M
)
и f
2
(
M
)
при М
→ М
0
стремятся каждая к конечному пределу, то:
а) 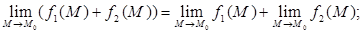
б) 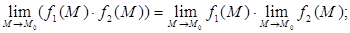
в) 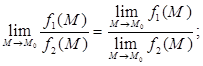  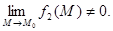
Пример 1.
Найти предел функции: 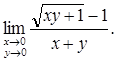
Решение. Преобразуем предел следующим образом:
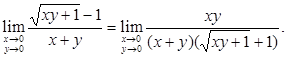
Пусть y
=
kx
, тогда 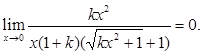
Пример 2.
Найти предел функции: 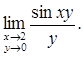
Решение. Воспользуемся первым замечательным пределом 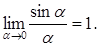 Тогда Тогда 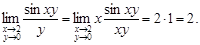
Пример 3.
Найти предел функции: 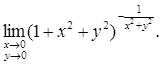
Решение. Воспользуемся вторым замечательным пределом 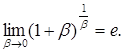 Тогда Тогда 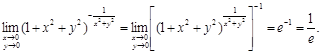
Непрерывность функции нескольких переменных
По определению функция f
(
x
,
y
)
непрерывна в точке (х
0
, у
0
), если она определена в некоторой ее окрестности, в том числе в самой точке (х
0
, у
0
) и если предел f
(
x
,
y
)
в этой точке равен ее значению в ней:
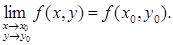 (1) (1)
Условие непрерывности f
в точке (х
0
, у
0
) можно записать в эквивалентной форме:
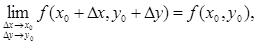 (1') (1')
т.е. функция f
непрерывна в точке (х
0
, у
0
), если непрерывна функция f
(х
0
+ Δх
, у
0
+ Δу)
от переменных Δх
, Δу
при Δх
= Δу =
0.
Можно ввести приращение Δи
функции и
= f
(
x
,
y
)
в точке (
x
,
y
)
, соответствующее приращениям Δх
, Δу
аргументов
Δи
= f
(х
+ Δх
, у
+ Δу)
– f
(
x
,
y
)
и на этом языке определить непрерывность f
в (
x
,
y
)
: функция f
непрерывна в точке (
x
,
y
)
, если
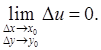 (1'') (1'')
Теорема.
Сумма, разность, произведение и частное непрерывных в точке (х
0
, у
0
) функций f
и φ есть непрерывная функция в этой точке, если, конечно, в случае частного φ (х
0
, у
0
) ≠ 0.
Постоянную с
можно рассматривать как функцию f
(
x
,
y
)
= с
от переменных x
,
y
. Она непрерывна по этим переменным, потому что
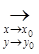 |f
(
x
,
y
)
– f
(х
0
, у
0
) | = |с – с
| = 0 0. |f
(
x
,
y
)
– f
(х
0
, у
0
) | = |с – с
| = 0 0.
Следующими по сложности являются функции f
(
x
,
y
)
= х
и f
(
x
,
y
)
= у
. Их тоже можно рассматривать как функции от (
x
,
y
)
, и при этом они непрерывны. Например, функция f
(
x
,
y
)
= х
приводит в соответствие каждой точке (
x
,
y
)
число, равное х
. Непрерывность этой функции в произвольной точке (
x
,
y
)
может быть доказана так:
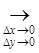 | f
(х
+ Δх
, у
+ Δу)
– f
(
x
,
y
)
| = |f
(х
+ Δх) – х
| = | Δх
| ≤ | f
(х
+ Δх
, у
+ Δу)
– f
(
x
,
y
)
| = |f
(х
+ Δх) – х
| = | Δх
| ≤  0. 0.
Если производить над функциями x
,
y
и постоянными действия сложения, вычитания и умножения в конечном числе, то будем получать функции, называемые многочленами от x
,
y
. На основании сформулированных выше свойств многочлены от переменных x
,
y
– непрерывные функции от этих переменных для всех точек (
x
,
y
)
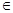 R
2
. R
2
.
Отношение P
/
Q
двух многочленов от (
x
,
y
)
есть рациональная функция от (
x
,
y
)
, очевидно, непрерывная всюду на R
2
, за исключением точек (
x
,
y
)
, где Q
(
x
,
y
)
= 0.
Функция
Р
(
x
,
y
)
= х
3
– у
2
+ х
2
у
– 4
может быть примером многочлена от (
x
,
y
)
третьей степени, а функция
Р
(
x
,
y
)
= х
4
– 2х
2
у
2
+ у
4
есть пример многочлена от (
x
,
y
)
четвертой степени.
Приведем пример теоремы, утверждающей непрерывность функции от непрерывных функций.
Теорема.
Пусть функция f
(
x
,
y
,
z
)
непрерывна в точке (
x
0
,
y
0
,
z
0
)
пространства R
3
(точек (
x
,
y
,
z
)
), а функции
x
= φ(u, v), y
= ψ(u, v), z
= χ(u, v)
непрерывны в точке (
u
0
,
v
0
)
пространства R
2
(точек (
u
,
v
)
). Пусть, кроме того,
x
0
= φ (
u
0
,
v
0
),
y
0
= ψ (
u
0
,
v
0
),
z
0
= χ (
u
0
,
v
0
)
.
Тогда функция F
(
u
,
v
) =
f
[ φ (
u
,
v
),
ψ (
u
,
v
),
χ (
u
,
v
)
] непрерывна (по
(
u
,
v
)
) в точке (
u
0
,
v
0
)
.
Доказательство. Так как знак предела можно внести под знак характеристики непрерывной функции, то
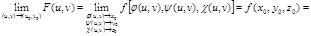 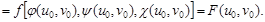
Теорема.
Функция f
(
x
,
y
)
, непрерывная в точке (х
0
, у
0
) и не равная нулю в этой точке, сохраняет знак числа f
(х
0
, у
0
) в некоторой окрестности точки (х
0
, у
0
).
По определению функция f
(
x
) =
f
(
x
1
, ..., хп
)
непрерывна в точке х
0
= (х
0
1
, ..., х
0
п
)
, если она определена в некоторой ее окрестности, в том числе и в самой точке х
0
, и если предел ее в точке х
0
равен ее значению в ней:
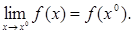 (2) (2)
Условие непрерывности f
в точке х
0
можно записать в эквивалентной форме:
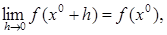 (2') (2')
т.е. функция f
(
x
)
непрерывна в точке х
0
, если непрерывна функция f
(х
0
+ h
)
от h
в точкеh
= 0.
Можно ввести приращение f
в точке х
0
, соответствующее приращению h
= (
h
1
, ..., h
п
)
,
Δh
f
(х
0
) =
f
(х
0
+ h
)
– f
(х
0
)
и на его языке определить непрерывность f
в х
0
: функция f
непрерывна в х
0
, если
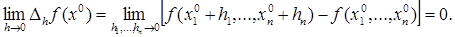 (2'') (2'')
Теорема.
Сумма, разность, произведение и частное непрерывных в точке х
0
функций f
(
x
)
и φ (
x
)
есть непрерывная функция в этой точке, если, конечно, в случае частного φ (х
0
)
≠ 0.
Замечание. Приращение Δh
f
(х
0
)
называют также полным приращением функции f
в точке х
0
.
В пространстве Rn
точек х
= (
x
1
, ..., хп
)
зададим множество точек G
.
По определению х
0
= (х
0
1
, ..., х
0
п
)
есть внутренняя точка множества G
, если существует открытый шар с центром в нем, полностью принадлежащий к G
.
Множество G
 Rn
называется открытым, если все его точки внутренние. Rn
называется открытым, если все его точки внутренние.
Говорят, что функции
х
1
= φ1
(t)
, ..., хп
=
φп
(t)
(a ≤ t ≤ b)
непрерывные на отрезке [a
, b
], определяют непрерывную кривую в Rn
, соединяющую точки х
1
= (х
1
1
, ..., х
1
п
)
и х
2
= (х
2
1
, ..., х
2
п
)
, где х
1
1
= φ1
(а)
, ..., х
1
п
=
φп
(а)
, х
2
1
= φ1
(
b
)
, ..., х
2
п
=
φп
(
b
)
. Букву t
называют параметром кривой.
Множество G
называется связным, если любые его две точки х
1
, х
2
можно соединить непрерывной кривой, принадлежащей G
.
Связное открытое множество называется областью.
Теорема.
Пусть функция f
(
x
)
определена и непрерывна на Rn
(во всех точках Rn
). Тогда множество G
точек х
, где она удовлетворяет неравенству
f
(
x
)
> с
(или f
(
x
)
< с
), какова бы ни была постоянная с
, есть открытое множество.
В самом деле, функция F
(
x
) =
f
(
x
)
– с
непрерывна на Rn
, и множество всех точек х
, где F
(
x
)
> 0, совпадает с G
. Пусть х
0
 G
, тогда существует шар G
, тогда существует шар
| х
– х
0
| < δ,
на котором F
(
x
)
> 0, т.е. он принадлежит к G
и точка х
0
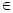 G
– внутренняя для G
. G
– внутренняя для G
.
Случай с f
(
x
)
< с
доказывается аналогично.
Таким образом, функция нескольких переменных f
(М)
называется непрерывной в точке М
0
, если она удовлетворяет следующим трем условиям:
а) функция f
(М)
определена в точке М
0
и вблизи этой точки;
б) существует предел 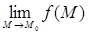 ; ;
в) 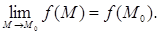
Если в точке М
0
нарушено хотя бы одно из этих условий, то функция в этой точке терпит разрыв. Точки разрыв могут образовывать линии разрыва, поверхность разрыва и т. д. Функция f
(М)
называется непрерывной в области G
, если она непрерывна в каждой точке этой области.
Пример 1.
Найти точки разрыва функции: z
=
ln
(
x
2
+ y
2
)
.
Решение. Функция z
=
ln
(
x
2
+ y
2
)
терпит разрыв в точке х
= 0, у
= 0. Следовательно, точка О
(0, 0) является точкой разрыва.
Пример 2.
Найти точки разрыва функции: 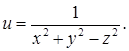
Решение. Функция не определена в точках, в которых знаменатель обращается в нуль, т.е. x
2
+ y
2
– z
2
= 0. Следовательно, поверхность конуса
x
2
+ y
2
= z
2
является поверхностью разрыва.
Заключение
Начальные сведения о пределах и непрерывности встречаются в школьном курсе математики.
В курсе математического анализа понятие предела является одним из основных. С помощью предела вводятся производная и определенный интеграл; пределы же являются основным средством в построении теории рядов. Понятие предела, впервые появившееся в 17 веке в работах Ньютона, используется и получает дальнейшее развитие в теории рядов. В этом разделе анализа исследуются вопросы, связанные с суммой бесконечной последовательности величин (как постоянных, так и функций).
Непрерывность функции дает представление о ее графике. Это означает, что график есть сплошная линия, а не состоит из отдельных разрозненных участков. Это свойство функции находит широкое применение в сфере экономики.
Поэтому понятия предела и непрерывности играют важную роль в исследовании функций нескольких переменных.
Список использованной литературы
1. Бугров Я.С., Никольский С.М. Высшая математика: Учебник для вузов. Том 2: Дифференциальное и интегральное исчисление. Москва: Дрофа, 2004 год, 512 с.
2. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридма М.Н. Высшая математика для экономистов. Москва: Юнити, 2000 год, 271 с.
3. Черненко В.Д. Высшая математика в примерах и задачах. Учебное пособие для вузов. Санкт-Петербург: Политехника, 2003 год, 703 с.
4. http://elib.ispu.ru/library/math/sem2/index.html
5. http://www.academiaxxi.ru/WWW_Books/HM/Fn/toc.htm
|