РЕФЕРАТ
На тему:
Обозначения и определения тензорной алгебры
Содержание
1. Индексные обозначения
2. Условие о суммировании
3. Сложение, умножение и свертывание объектов
4. Симметричные и антисимметричные объекты
Литература
1. Индексные обозначения
Система индексных обозначений составляет столь значительную часть тензорного исчисления, что читатель, освоившись однажды с ее особенностями, сможет идти дальше самостоятельно. Поэтому мы посвятим настоящую главу только самой системе обозначений, изложив кратко ее применение лишь к теории определителей, и отложим до следующей главы собственно тензорную алгебру. Если нам дана совокупность трех независимых переменных, то они могут быть обозначены тремя различными буквами, например х, у, z, но мы считаем более удобным обозначать переменные данной совокупности одной и той же буквой, различая их посредством индексов. Таким образом, мы можем записать три переменные в виде xv х2, х3, или в более компактной форме:

Здесь мы написали индекс г внизу, но в равной мере мы могли бы использовать вместо этого верхний значок, так что переменные были бы записаны в виде х1, х2, х3, или

Понятно, что хг
не означает возведения х в r-ю степень; индекс г используется просто для того, чтобы различить три переменные. Впоследствии мы будем использовать как верхние, так и нижние индексы; в следующей главе мы припишем положению индекса специальный смысл. В дальнейшем мы увидим, что для наших переменных удобна форма записи 2), а не 1).
Однородная линейная функция переменных обычно записывается в виде

где а,, а2, а3 —константы. Таким образом, коэффициенты линейной формы могут быть записаны в виде

Объекты, которые, подобно хт и ат, зависят только от одного индекса, называются объектами первого порядка, а отдельные буквы с индексами х1, х2, х3 и аг, а2, а3 называются элементами или составляющими объекта. Объекты первого порядка, имеющие три составляющие, назовемтрехмерными. Имеются два типа объектов первого порядка, а именно те, у которых индекс вверху, и те, у которых индекс внизу; следовательно, все объекты первого порядка принадлежат к одному из двух типов

С другой стороны, однородная квадратичная функция трех переменных имеет вид

где amn
—константы. Мы видим, что коэффициенты квадратичной формы зависят от двух индексов и записываются так:

Объекты, которые зависят от двух индексов, называются объектами второго порядка. Из того, что индексы бывают верхние и нижние, следует, что объекты второго порядка могут быть трех типов:

Легко видеть, что в этом случае каждый объект имеет 9 составляющих.
Аналогично можно получить объекты третьего порядка, которые будут зависеть от трех индексов и могут принадлежать к любому из четырех типов:

Здесь каждый объект содержит З3 или 27 составляющих. Мы можем
продолжать это построение и получить объекты любого порядка. Для законченности этой последовательности мы назовем объект а, не имеющий индексов, объектом нулевого порядка. Мы взяли число измерений равным трем лишь для определенности. Все, что было сказано выше, применимо также к любому числу измерений, если условиться, что число значений, пробегаемых индексом, равно ¦ числу измерений. Например, если число измерений равно четырем, следует считать, что индексы могут пробегать значения от 1 до 4, а но от 1 до 3, как предполагалось выше.
2. Условие о суммировании
Мы введем теперь два важных условия относительно индексов. В тензорном исчислении мы часто имеем дело с суммами типа C) и E); нетрудно заметить, что в этих формулах индексы, по которым идет суммирование, появляются дважды. Наши формулы можно сделать компактнее, если избавиться от знака 2- Это может быть осуществлено, если принять, что знак 2 будет подразумеваться в любом случае, когда в одночленном выражении индекс повторяется. Тогда C) можно записать так:

а (5) примет вид

Единственное неудобство в применении нашего условия возникает в том случае, когда мы желаем выписать один член какой-либо из сумм (8) или (9). Нам это потребуется очень редко, но мы запасемся для этого случая соглашением, что условие о суммировании применяется только, когда повторяющийся индекс записан малой буквой, а использование заглавных букв для повторяющихся индексов не означает суммирования. Таким образом, отдельные члены сумм (8) и (9) будут обозначаться соответственно. Наше первое условие, следовательно, читается так:
Повторяющийся малый латинский индекс означает суммирование от 1 до 3.
Так как повторяющийся индекс означает суммирование от 1 до 3, то применение какой-нибудь специальной буквы для повторяющихся индексов не обязательно, и мы можем заменить ее любой буквой, которая нам удобна, без изменения значения рассматриваемого выражения. Таким образом,

По этой причине повторяющийся индекс часто называют немым. Индекс, который в каком-нибудь одночленном выражении не повторяется, назовем свободным. Таким образом, все индексы в формулах D), F) и G) —свободные индексы; следует отметить, что в. этих формулах свободные индексы пробегают значения от 1 до 3. Мы имеем, следовательно, наше второе условие:
Свободные (неповторяющиеся) малые латинские индексы пробегают значения от 1 до 3.
Например, объект второго порядка будет теперь записываться в виде

без какого-нибудь дополнительного упоминания о числе значений, пробегаемых г и s. Другими словами, ara означает любую из девяти составляющих

Отметим, что почти всегда немой индекс будет появляться в одним верхнем и в одном нижнем положении. Поскольку это окажется возможным, в настоящей главе мы будем придерживаться такого расположения индексов.
3. Сложение, умножение и свертывание объектов
В алгебре объектов со многими индексами имеются три главные операции, которые называются сложением, умножением и свертыванием.
а) Сложение. Эта операция применима только к объектам одного и того же порядка и типа. Если нам даны два объекта одного и того же порядка и типа и если мы складываем каждую составляющую первого объекта с соответствующей составляющей второго, то мы, очевидно, приходим к объекту того же порядка и типа, что и слагаемые. Этот процесс есть операция сложения, и результирующий объект называется суммой двух объектов. Таким образом, если arst и brst — два объекта третьего порядка, то объект 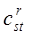 , определенный равенством , определенный равенством

есть сумма 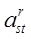 и и 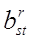 . Мы подразумеваем здесь алгебраическую сумму; поэтому вычитание включено сюда как частный случай. Кроме того, эта операция может быть распространена непосредственно на случай любого количества объектов, если только они все одного и того же порядка и типа. . Мы подразумеваем здесь алгебраическую сумму; поэтому вычитание включено сюда как частный случай. Кроме того, эта операция может быть распространена непосредственно на случай любого количества объектов, если только они все одного и того же порядка и типа.
б) Умножение. Мы сейчас определим произведение двух объектов. Если мы берем два объекта любого типа и умножаем каждую составляющую первого объекта на каждую составляющую второго, мы получаем объект, порядок которого равен сумме порядков двух исходных объектов; этот результирующий объект называется произведением двух объектов. Например, если ar
st
— объект третьего порядка и bmn
— объект второго порядка, то мы видим, что объект сrmn
, составляющие которого определяются равенством

есть объект пятого порядка и является произведением ar
st
и bmn
. Этот процесс, конечно, может быть распространен на любое количество объектов.
в) Свертывание. Процесс свертывания может быть пояснен на примере. Возьмем объект пятого порядка

который имеет как верхние, так и нижние индексы. Если мы теперь положим и равным р, мы получим объект arsfp, и так как р является теперь повторяющимся индексом, то необходимо произвести суммирование от 1 до 3, в соответствии с нашим условием. Итак, полученный таким путем новый

Мы видим, что наш новый объект A2) —третьего по- рядка, т. е. его порядок на два ниже, чем порядок исходного объекта. Операция может быть, очевидно, повторена несколько раз, т. е. мы можем произвести свертывание относительно любой пары индексов, один из которых является нижним,, а другой—верхним. В приведенном выше примере мы можем произвести свертывание еще раз по индексам rp, получив объект первого порядка

Имеется еще одна операция, называемая внутренним умножением, которая не является новой, так как в действительности она является комбинацией умножения и свертывания. Чтобы выполнить эту операцию над двумя объектами, мы сначала перемножаем их, а затем свертываем произведение по нижнему индексу одного объекта и верхнему индексу другого. Таким образом, внутреннее произведение двух объектов есть, например,

4. Симметричные и антисимметричные объекты
Если мы имеем объект аmn
с двумя нижними индексами, то может случиться, что каждая из составляющих не изменится по величине и знаку при перемене мест индексов, т. е.

Такой объект называют симметричным. В более общем случае объект, имеющий любое число нижних индексов, называется симметричным относительно двух из них, если составляющие не изменяются при перемене мест этих двух индексов. Объект называется абсолютно симметричным относительно нижних индексов, если при перемене мест любых двух из них составляющие не изменяются. Абсолютно симметричный объект третьего порядка будет, следовательно, удовлетворять соотношениям

С другой стороны, объект аmn
называется антисимметричным, если перемена мест индексов изменяет знак составляющей, но не изменяет ее численного значения; в таком случае мы имеем

Эти равенства, выписанные полностью, выглядят так:

откуда мы немедленно заключаем, что  Как и выше, объект может быть антисимметричным либо относительно двух каких-нибудь нижних индексов, либо относительно всех пар индексов; в последнем случае объект называется абсолютно антисимметричным. Абсолютно антисимметричный объект третьего порядка должен удовлетворять соотношениям Как и выше, объект может быть антисимметричным либо относительно двух каких-нибудь нижних индексов, либо относительно всех пар индексов; в последнем случае объект называется абсолютно антисимметричным. Абсолютно антисимметричный объект третьего порядка должен удовлетворять соотношениям

Все сказанное выше о симметрии и антисимметрии в равной степени применимо и к верхним индексам.
Литература
1. Рашевский П.К., Риманова геометрия и тензорный анализ, Гостехиздат, Москва, 1953.
2. Гуревич Г.В., Основы теории алгебраических инвариантов, Гостехиздат, Москва, 1948.
3. Труды семинара по векторному и тензорному анализу, вып. I—X, Гостехиздат, Москва, 1933, 1956.
4. Каган В.Ф., Основы теории поверхностей, т, 1, Гостехиздат, Москва, 1943, т. Ц, Москва, 1947.
|