1)Дифференциальное уравнение. Общее решение. Частное решение. Задача Коши
Диф.ур-м наз-ся ур-е
, связывающее независим.перем. х сикомую ф-ию у, и ее производные.
 . .
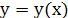 . => ОДУ . => ОДУ
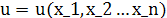 . .
Общим решением
ОДУ первого порядка назся ф-ия 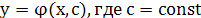 , удовл.след.условиям: , удовл.след.условиям:
1) явл.решением ур-я явл.решением ур-я 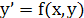 при при 
2)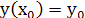 ∃ такое значение произв.пост. ∃ такое значение произв.пост. 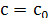 , при котором , при котором  удовл.данному нач.условию. удовл.данному нач.условию. 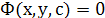 -общий интеграл -общий интеграл
Частн.решением
обыкн.диф.ур-я первого порядка наз-ся ф-ия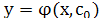 кот.получ.из общего решения кот.получ.из общего решения  ) при конкретном значении с. ) при конкретном значении с.
Задача Коши
- задача нахождения обыкнов. диф.ур-я удовлет. начальному условию 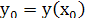
2)Уравнение с разделяющимися переменными.
Наз-ся обыкновенное уравнеие1 порядка, кот.прив.к виду: 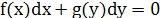
К ним относ. диф.ур.вида:
1)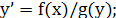 2) 2) 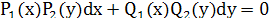 умножим на умножим на 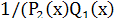 => =>
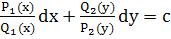 .- ур-е с раздел.перем. .- ур-е с раздел.перем.
3)Однородные уравнения. Уравнения, приводящиеся к однородным
Ф-ия
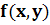 наз-ся однород.ф-ей наз-ся однород.ф-ей
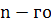 порядка или n-ой измерениями относительно переем порядка или n-ой измерениями относительно переем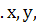 если при если при 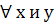 . .
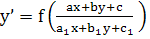 . аргументом явл.дробь. . аргументом явл.дробь.
4)Уравнения в полных дифференциалах. Интегрирующий множитель
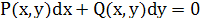 .Ур-е наз-ся ур-ем в полных диф.если сущ-ет такоя ф-ия .Ур-е наз-ся ур-ем в полных диф.если сущ-ет такоя ф-ия
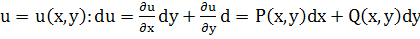 . .
5)Линейное дифференциальное уравнение первого порядка
ДУ 1 порядка наз-ся линейным, если его можно записать в виде 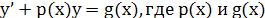 – заданные ф-ии, в частности – постоянные. – заданные ф-ии, в частности – постоянные.
а)Метод Бернулли
Решение ур-я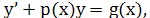 ищется в виде произведения двух других ф-ий, т.е. сРер помощью подстановки ищется в виде произведения двух других ф-ий, т.е. сРер помощью подстановки 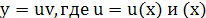 – неизвестные ф-ии х, причем одна из них произвольна (но ≠0) – днйствительно любую ф-ию у(х) можно записать как: – неизвестные ф-ии х, причем одна из них произвольна (но ≠0) – днйствительно любую ф-ию у(х) можно записать как:
 , , 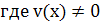 ).Тогда ).Тогда 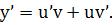 Подставляя выражение у и у’ в Подставляя выражение у и у’ в 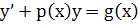 получаем: получаем:  Подберем ф-ю Подберем ф-ю 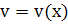 так что бы так что бы
 . Итак, . Итак, 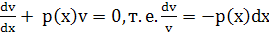 , интегрируя получаем: , интегрируя получаем:
 Ввиду свободы выбора ф-ии Ввиду свободы выбора ф-ии 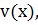 можно принять с=1=> v= можно принять с=1=> v=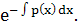
Подставляя найденную ф-ию в ур-е 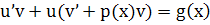 получаем: получаем:  . .
Получено уравнение с раздел.перем.Решаем его: 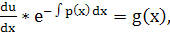
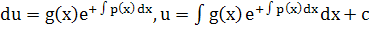 . .
Возвращаясь к переменной у, получеам решение исходного ДУ 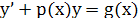
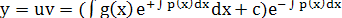 .сходного ДУ переменной у, получаем решение го поля. Нахождение потенциала по заданному примеру. .сходного ДУ переменной у, получаем решение го поля. Нахождение потенциала по заданному примеру.
б)Метод Лагранжа
Рассмотрим однородное уравнение 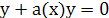 . Очевидно, это уравнение с разделяющимися переменными, его решение: . Очевидно, это уравнение с разделяющимися переменными, его решение: 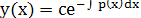
Решения исходного уравнения будем искать в виде: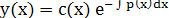
Подставив полученное решение в исходное уравнение: 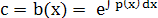 , получаем: c , получаем: c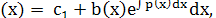 где c1 — произвольная константа. где c1 — произвольная константа.
Таким образом, решение исходного уравнения можно получить путем подстановки c(x) в решение однородного уравнения:  . .
6)Уравнение Бернулли
Ур-е вида 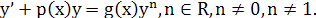
Если n=0, то ДУ – линейное, а при n=1 – с раздел.переменными.
Данное ур-е решается двумя способами:
Первый способ
Заменой
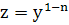 , уравнение приводится к линейному , уравнение приводится к линейному  и может быть решено методом Лагранжа (вариации постоянной) или методом интегрирующего множителя. и может быть решено методом Лагранжа (вариации постоянной) или методом интегрирующего множителя.
Второй способ
Заменим 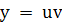 . .
Тогда 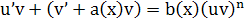 . .
Подберем 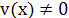 так, чтобы было так, чтобы было
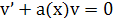 . .
для этого достаточно решить уравнение с разделяющимися переменными 1-го порядка.
После этого для определения 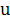 получаем уравнение получаем уравнение
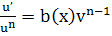 - уравнение с разделяющимися переменными. - уравнение с разделяющимися переменными.
7)Уравнение неразрешенное относительно
 Метод введения параметра Метод введения параметра
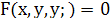 – относительно производной – относительно производной 
a)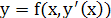
б)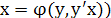
в)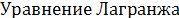
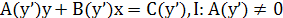 . .
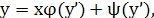 где 𝜑и 𝜓известные ф-ии от где 𝜑и 𝜓известные ф-ии от  наз-ся ур-ем Лагранжа. наз-ся ур-ем Лагранжа.
Введем вспомогат.параметр, положив у’=p. Тогда ур-е 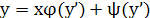 примет вид: у=𝜑(p)+𝜓(p). Дифференц.по х, получим: примет вид: у=𝜑(p)+𝜓(p). Дифференц.по х, получим:
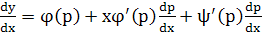 , т.е. , т.е.  или или 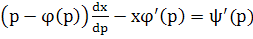 - линейное ур-е относит.неизвестной - линейное ур-е относит.неизвестной 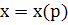 , решив его найдем: , решив его найдем: 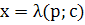 . Исключая параметр р из . Исключая параметр р из 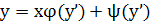 и и 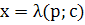 получаем общий интеграл ур-я получаем общий интеграл ур-я 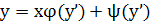 в виде в виде 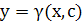 . При делении на . При делении на 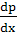 могли быть потеря решения, для которых могли быть потеря решения, для которых  ,т.е. ,т.е.  . Это значение . Это значение 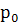 явл.корнем ур-я явл.корнем ур-я 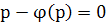 . Решение . Решение  явл.особым для ур-я явл.особым для ур-я 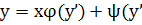
г)Уравнение Клеро
Рассмотрим частный случай уравнения Лагранжа при 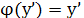 Уравнение принимает вид Уравнение принимает вид

и называется урaвнeниeм Клеро. Положив 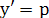 , получаем: , получаем:
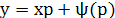 . .
Дифференцируя по х, имеем: 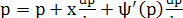 или или  . .
Если 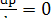 , то , то  . Поэтому, с учетом . Поэтому, с учетом 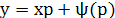 , ДУ , ДУ  имеет общее решение имеет общее решение  . .
Если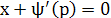 , получаем частное решение уравнения в параметрической форме: , получаем частное решение уравнения в параметрической форме:
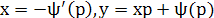 . .
Это решение - особое решение уравнения Клеро: оно не содержится в формуле общего решения уравнения.
8)Особое решение
9)Линейное уравнение
n
-го порядка. Запись с помощью
L
. Свойства
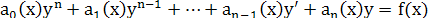 , , . .
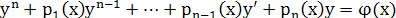 . .
Если коэф.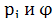 непрер.,то т.осущ.и един.доказана. непрер.,то т.осущ.и един.доказана.
Линейный диф.оператор(ЛДО): 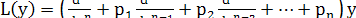 , то , то 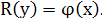
Св-ва:
1)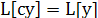 ; 2) ; 2)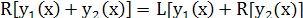 ; 3) ; 3) 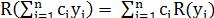 . .
10)Линейная независимость функции. Определитель Вронского. Теорема линейной зависимости
.
Функции 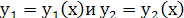 называются линейно независимыми
на интервале называются линейно независимыми
на интервале 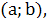 если равенство если равенство 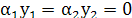 , где , где  , выполняется тогда и только тогда, , выполняется тогда и только тогда,
когда 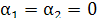
Средством изучения линейной зависимости сестемы ф-ий явл.так называемый определитель Вронсоко
или вронскиан. Для двух диф.ф-ий 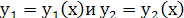 вронскиан имеет вид: вронскиан имеет вид:
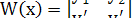 . .
Теорема лин. зависимости
: Если диф.ф-ии 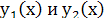 лин.зависимы на лин.зависимы на 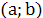 , то определитель Вронского на этом интервале тождественно равен нулю. , то определитель Вронского на этом интервале тождественно равен нулю.
Так как функции 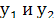 линейно зависимы, то в равенстве линейно зависимы, то в равенстве 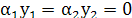 значение значение  отлично от нуля. Пусть отлично от нуля. Пусть  , тогда , тогда  поэтому для любого поэтому для любого 
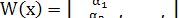 . .
11)Если линейно независимы
⟹
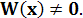 Доказательство Доказательство
Если функции 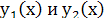 - линейно независимые решения уравнения - линейно независимые решения уравнения 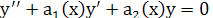 на на 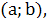 то определитель Вронского на этом интервале нигде не обращается в нуль. то определитель Вронского на этом интервале нигде не обращается в нуль.
Из теоремы следует, что вронскиан не равен нулю ни в одной точке интервала (
a
;
b
)
тогда и только тогда, когда частные решения линейно независимы.
12 Фундаментальная система решений. Теорема существования фундаментальной системы решений. Доказательство
Фундаментальная система решений (ФСР)
представляет собой набор линейно независимых решений однородной системы уравнений.
Совокупность любых двух линейно независимых на интервале (a; b) частных решений  ЛОДУ второго порядка определяет фундаментальную систему решений
этого уравнения: любое произвольное решение может быть получено как комбинация ЛОДУ второго порядка определяет фундаментальную систему решений
этого уравнения: любое произвольное решение может быть получено как комбинация 
Теорема (о ФСР)
Если два частных решения  ЛОДУ ЛОДУ  образуют на интервале (а;b) фундаментальную систему, то общим решением этого уравнения является функция образуют на интервале (а;b) фундаментальную систему, то общим решением этого уравнения является функция
 , где , где 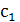 и и 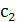 - произвольные постоянные. - произвольные постоянные.
13)
Построение общего решения ЛОДУ
13.Построение общего решения ЛНДУ.
14.ЛДУ n- го порядка с постоянным коэффициентом. Общее решение. ЛОДУ, характеристические мн-н. Корни простые.
15.ЛОДУ, характеристические мн-н. Корни кратные.
16.ЛНДУ. Метод подбора частного решения.
18. Системы ДУ. Метод сведения к ДУ n-го порядка.
19.Системы ДУ. Метод интегрируемых комбинаций.
20. Система ЛДУ. Матричная запись. Свойства
21 Зависимые и независимые решения. Определитель Вронского.
22.Система ЛОДУ. Свойства
23.Фундаментальная система решений. Построение общего решения.
24.ЛН системы. Метод вариаций.
25.Л О системы с постоянным коэффициентом. Метод Эйлера.
уравнение линейный решение бернулли
|