План
Задача 1
Задача 2
Задача 3
Задача 4
Задача 5
Задача 6
Задача 7
Задача 8
Список литературы
По данным приложения 1 по своему варианту выполните следующую обработку статистического материала:
1. Построить группировку предприятий по величине основных фондов, образовав 5 групп с равновеликими интервалами группировки. Приведите расчет равновеликого интервала группировки по формуле. Рассчитать коэффициент корреляции рангов Спирмена. Объясните экономический смысл рассчитанного показателя и сделайте выводы.
2. Определите по каждой группе:
- число заводов;
- стоимость основных производственных фондов - всего и в среднем на один завод;
- стоимость товарной продукции - всего и в среднем на один завод
Результаты представьте в табличной виде, проанализируйте их и сделайте выводы.
Решение
Таблица 1
Исходные данные
| № предприятия |
Среднегодовая стоимость промышленно- производственных основных фондов, млрд. руб. |
Товарная продукция в оптовых ценах предприятия, млрд. руб. |
| 1 |
10,3 |
11,2 |
| 2 |
14,2 |
16,8 |
| 3 |
15,8 |
18,2 |
| 4 |
17,7 |
20,1 |
| 5 |
18,5 |
21,2 |
| 6 |
19,3 |
24,1 |
| 7 |
21,2 |
24,7 |
| 8 |
22,5 |
25,4 |
| 9 |
24,8 |
24,1 |
| 10 |
26,7 |
27,7 |
| 11 |
12,9 |
14,0 |
| 12 |
15,4 |
17,2 |
| 13 |
16,1 |
19,3 |
| 14 |
18,3 |
19,6 |
| 15 |
18,9 |
23,4 |
| 16 |
19,8 |
24,5 |
| 17 |
21,1 |
25,0 |
| 18 |
23,3 |
25,7 |
| 19 |
25,9 |
25,0 |
| 20 |
30,3 |
31,2 |
Таблица 2
Ранжирование исходных данных
| № предприя |
Среднегодовая стоимость промышленно- производственных основных фондов, млрд. руб. |
Товарная продукция в оптовых ценах предприятия, млрд. руб. |
| 1 |
10,3 |
11,2 |
| 11 |
12,9 |
14 |
| 2 |
14,2 |
16,8 |
| 12 |
15,4 |
17,2 |
| 3 |
15,8 |
18,2 |
| 13 |
16,1 |
19,3 |
| 4 |
17,7 |
20,1 |
| 14 |
18,3 |
19,6 |
| 5 |
18,5 |
21,2 |
| 15 |
18,9 |
23,4 |
| 6 |
19,3 |
24,1 |
| 16 |
19,8 |
24,5 |
| 17 |
21,1 |
25 |
| 7 |
21,2 |
24,7 |
| 8 |
22,5 |
25,4 |
| 18 |
23,3 |
25,7 |
| 9 |
24,8 |
24,1 |
| 19 |
25,9 |
25 |
| 10 |
26,7 |
27,7 |
| 20 |
30,3 |
31,2 |
Построим статистический ряд распределения предприятий по величине основных фондов.
n = 5 - количество групп.
Величина равного интервала рассчитывается по формуле:
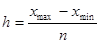 . .
xmax
= 10,3 млн.руб.; хmin
= 30,3 млн.руб.
h = (30,3-10,3)/5 = 4 млн.руб.
В начале построим рабочую таблицу с интервалом h = 4 млн.руб.
Таблица 3
Распределение предприятий по величине основных фондов
| № группы |
Группы предприятий по величине ОФ, млн. руб. |
№ предприятия |
Среднегодовая стоимость промышленно- производственных основных фондов, млрд. руб.(X) |
Товарная продукция в оптовых ценах предприятия, млрд. руб. (Y) |
| I |
10,3-14,3 |
1 |
10,30 |
11,20 |
| 11 |
12,90 |
14,00 |
| 2 |
14,20 |
16,80 |
| всего |
3 |
37,40 |
42,00 |
| в среднем по группе |
12,47 |
14,00 |
| II |
14,3-18,3 |
12 |
15,40 |
17,20 |
| 3 |
15,80 |
18,20 |
| 13 |
16,10 |
19,30 |
| 4 |
17,70 |
20,10 |
| 14 |
18,30 |
19,60 |
| всего |
5 |
83,30 |
94,40 |
| в среднем по группе |
16,66 |
18,88 |
| III |
18,3-22,3 |
5 |
18,50 |
21,20 |
| 15 |
18,90 |
23,40 |
| 6 |
19,30 |
24,10 |
| 16 |
19,80 |
24,50 |
| 17 |
21,10 |
25,00 |
| 7 |
21,20 |
24,70 |
| 8 |
22,50 |
25,40 |
| всего |
7 |
141,30 |
168,30 |
| в среднем по группе |
20,19 |
24,04 |
| IV |
22,3-26,3 |
18 |
23,30 |
25,70 |
| 9 |
24,80 |
24,10 |
| 19 |
25,90 |
25,00 |
| всего |
3 |
74,00 |
74,80 |
| в среднем по группе |
24,67 |
24,93 |
| V |
26,3-30,3 |
10 |
26,70 |
27,70 |
| 20 |
30,30 |
31,20 |
| всего |
2 |
57,00 |
58,90 |
| в среднем по группе |
28,50 |
29,45 |
| итого |
20 |
393,00 |
438,40 |
| среднее |
19,65 |
21,92 |
По данным таблицы 3 строим итоговую аналитическую таблицу.
Таблица 4
Группировка предприятий по величине ОФ
| № п/п |
Группы предприятий |
Число заводов |
Стоимость основных производственных фондов |
Товарная продукция в оптовых ценах предприятия, млрд. руб. |
| всего |
В среднем на один завод |
всего |
В среднем на один завод |
| 1 |
10,3-14,3 |
3 |
37,40 |
12,47 |
42,00 |
14,00 |
| 2 |
14,3-18,3 |
5 |
83,30 |
16,66 |
94,40 |
18,88 |
| 3 |
18,3-22,3 |
7 |
141,30 |
20,19 |
168,30 |
24,04 |
| 4 |
22,3-26,3 |
3 |
74,00 |
24,67 |
74,80 |
24,93 |
| 5 |
26,3-30,3 |
2 |
57,00 |
28,50 |
58,90 |
29,45 |
| Итого |
20 |
393,00 |
19,65 |
438,40 |
21,92 |
Из таблицы видно, что стоимость основных производственных фондов в среднем на один завод наименьшая в группе 1 с интервалом 10,3 – 14,3 и равна 12,47 млн.руб. При этом товарная продукция в среднем на один завод также в этой группе наименьшая и равна 14. Наибольшая стоимость основных производственных фондов в среднем на один завод в группе 5 с интервалом 26,3-30,3 и равна 28,5. Наибольший результат по товарной продукции в оптовых ценах предприятия в среднем на один завод также в группе 5 и равна 29,45.
Из расчетов можно сделать вывод, что товарная продукция в оптовых ценах предприятия напрямую зависит от стоимости основных производственных фондов.
Найдем коэффициент корреляции рангов Спирмэна, который основан на рассмотрении разности рангов значений факторного и результативного признаков по формуле:
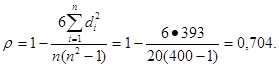
Поскольку коэффициенты корреляции рангов могут изменяться в пределах от -1 до + 1. по результатам расчетов коэффициента Спирмэна можно предположить наличие достаточно тесной прямой зависимости между стоимостью основных производственных фондов и товарной продукцией в оптовых ценах предприятия.
В результате контрольной выборочной проверки расфасовки чая осуществлена 25% механическая выборка по способу бесповторного отбора, в результате которой получено следующее распределение пачек чая по массе:
Таблица 5
Исходные данные
| Масса 1 пачки чая. Г |
Число пачек чая. шт. |
До 49
48-50
50-51
51-52
52 и выше
|
17
52
21
7
3
|
| Итого: 100 |
По результатам выборочного обследования определите:
1. Среднюю массу 1 пачки чая.
2. Дисперсию и среднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0.954 возможные пределы средней массы пачки чая во всей партии продукции.
5. С вероятностью 0.997 возможные пределы удельного веса пачек чая с массой до 49г и свыше 52г во всей партии продукции.
Решение
Таблица 6
Промежуточные вычисления
| Масса 1 пачки чая. г |
Число пачек чая. шт.,f
|
Середина
интервала
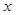
|
Расчетные значения |
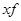
|
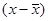
|
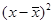 |
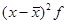 |
| До 49 |
17 |
48,5 |
824,5 |
-1,27 |
1,61 |
27,42 |
| 49-50 |
52 |
49,5 |
2574 |
-0,27 |
0,07 |
3,79 |
| 50-51 |
21 |
50,5 |
1060,5 |
0,73 |
0,53 |
11,19 |
| 51-52 |
7 |
51,5 |
360,5 |
1,73 |
2,99 |
20,95 |
| 52 и выше |
3 |
52,5 |
157,5 |
2,73 |
7,45 |
22,36 |
| Итого |
100 |
- |
4977 |
85,71 |
1. Найдем среднюю массу пачки чая.
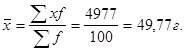
2. Найдем дисперсию и среднее квадратическое отклонение
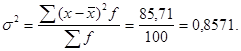
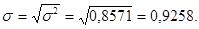
3. Определим коэффициент вариации, %
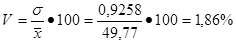 % %
Таким образом, наблюдается небольшая колеблемость веса пачки, поскольку коэффициент вариации признака составляет 1,86%.
4. Границы генеральной средней (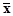 ) определяются значением выборочной средней ( ) определяются значением выборочной средней (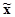 ) и предельной ошибкой выборки для средней ( ) и предельной ошибкой выборки для средней (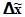 ). Они записываются формулой; ). Они записываются формулой;
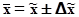 , где , где 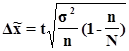
n - численность единиц выборочной совокупности;
N - численность единиц генеральной совокупности.
Значение коэффициента доверия t зависит от заданной степени вероятности. При вероятности 0,954 этот коэффициент t = 2,
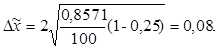
С вероятностью 0,954 возможные пределы, в которых ожидается средний вес:
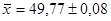 . .
5. число пачек чая с массой до 49г и свыше 52г в выборке – 20.
Доля этих пачек в выборке:
W=20/100=0,2.
При выборочном измерении доли альтернативного признака границы генеральной доли совокупности, обладающей нужным признаком, записываются равенством:
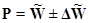 , ,
где Δ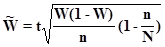
- предельная ошибка выборки для доли. Вероятности 0,997 соответствует значение t = 3.
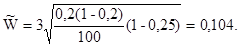
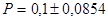
С вероятность 0,997 возможные пределы доли пачек чая с массой до 49г и свыше 52г во всей партии продукции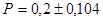 . .
Урожайность пшеницы в районе характеризуется следующими данными:
Таблица 7
Интервальный ряд динамики "А"
| Показатель \ годы |
1998 |
1999 |
2000 |
2000 |
2002 |
| Средняя урожайность, ц/га |
34,0 |
34,8 |
36,6 |
39,3 |
42,8 |
На основе имеющихся данных:
1. Определите все аналитические показатели ряда динамики "А".
2. Покажите взаимосвязь цепных и базисных темпов роста.
3. Приведите графическое изображение динамики средней урожайности.
Таблица 8
Моментный ряд динамики "В"
| Показатели \ Дата |
на 1.I. |
на 1.II. |
на 1.III. |
на.1.IV. |
| Списочная численность работников, чел |
402 |
406 |
403 |
408 |
4. Приведите расчет среднесписочной численности работников предприятия за квартал по данным пометного рада динамики "Б" по формуле средней хронологической длямоментного ряда.
основной фонд себестоимость продукция
Решение
1. Средняя урожайность за 1998-2002 гг. считается как средняя арифметическая:
Уср.= (34+34,8+36,6+39,3+42,8)/5=37,5 ц/га.
Цепные приросты в 1998-2002гг. по годам исчисляется по формуле:
∆Уцепной = Уi
– Yi
-1.
Абсолютные базисные приросты к 1998 г.(базису)
∆Убазисный = Уi
– Y0
;
Темпы роста цепные:
Темпы роста базисные
Tрбазисный
= Yi
*
100/Y0
.
Темп прироста цепной:
∆Tц
i
=∆Уц
i
/Yi
-1
*100.
Темп прироста базисный к (1998 г.):
∆Tб
i
=∆Уб
i
/Y0
*100.
Абсолютное значение 1% прироста в данном периоде есть сотая часть достигнутого уровня в предыдущего периоде. В связи с этим расчет абсолютного значения 1% прироста базисным методом не имеет смысла, ибо для каждого периода это будет одна и та же величина-сотая часть уровня базисного периода.
Полученные результаты представим в таблице.
Таблица 9
Средняя урожайность в 1998-2002 гг.
| Год |
Средняя урожайность, ц/га |
Абсолютные приросты, ц/га. |
Темпы роста, % |
Темп прироста,% |
Абсолютное содержание одного процента прироста, ц/га |
| цепные |
Базисные |
цепные |
Базисные |
цепные |
Базисные |
| 1998 |
34 |
| 1999 |
34,8 |
0,8 |
0,8 |
102,35 |
102,35 |
2,35 |
2,35 |
0,34 |
| 2000 |
36,6 |
1,8 |
2,6 |
105,17 |
107,65 |
5,17 |
7,65 |
0,348 |
| 2001 |
39,3 |
2,7 |
5,3 |
107,38 |
115,59 |
7,38 |
15,59 |
0,366 |
| 2002 |
42,8 |
3,5 |
8,8 |
108,91 |
125,88 |
8,91 |
25,88 |
0,393 |
| Итого |
187,5 |
8,8 |
- |
- |
- |
- |
- |
- |
Среднегодовой коэффициент роста рассчитывается по формуле:
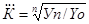 . .
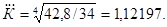
Соответственно средний темп роста составит 112,197%.
2. Сумма цепных приростов равна темпу роста базисному в 2002 г.
0,8+1,8+2,7+3,5=8,8,%.
3.
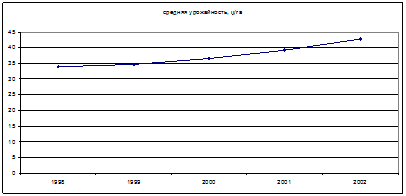
Рис.1. Динамика средней урожайности
Таким образом, в 1998-2002 наблюдался устойчивый рост урожайности.
4. Приведем расчет остатков оборотных средств по данным моментного ряда динамики "Б" по формуле средней хронологической для моментного ряда.
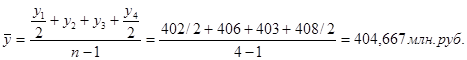
Себестоимость и объем производства пива характеризуется следующими данными:
Таблица 10
Исходные данные
| Марки пива |
Себестоимость1 бутылки ,руб. |
Выработано продукции, тыс. бутылок |
| 2002 |
2003 |
2002 |
2003 |
| Балтика |
20 |
23 |
1835 |
1910 |
| Клинское |
13 |
15 |
1404 |
1415 |
Определите:
1. Индивидуальные и общий агрегатный индексы себестоимости продукции.
2. Индивидуальные и общий агрегатный индексы физического объема продукций.
3. Общий индекс затрат на продукцию (издержек производства).
4. Индекс себестоимости переменного состава и структурных сдвигов,
Решение
Таблица 11
Промежуточные вычисления
| Виды продукции |
Себестоимость единицы продукции, руб. |
Кол-во произведенной продукции, тыс.бутылок. |
индексы
|
стоимость произведенной продукции, тыс.руб.
|
| zo |
z1 |
q0 |
q1 |
iq=q1/q0 |
i=z1/z0 |
z0*q0 |
z0*q1 |
z1*q0 |
z1*q1 |
| Балтика |
20 |
23 |
1835 |
1910 |
1,0409 |
1,1500 |
36700 |
38200 |
42205 |
43930 |
| Клинское |
13 |
15 |
1404 |
1415 |
1,0078 |
1,1538 |
18252 |
18395 |
21060 |
21225 |
| итого |
3239 |
3325 |
54952 |
56595 |
63265 |
65155 |
Найдем индивидуальный и общий агрегатный индексы себестоимости продукции
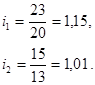
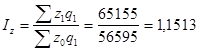 или 115,13%. или 115,13%.
Индивидуальный индекс показывает, что себестоимость Балтики «Подмосковного» 2003 году по сравнению с 2002 годом возросла на 15%, а батона горчичного– на 10%.
Общий агрегатный индекс показывает, что в 2003 г. по сравнению с 2002 г. себестоимость продукции возросла на 15,12%.
2. Найдем индивидуальный и общий индексы физического объема продукции
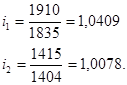
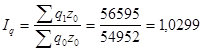 или 102,99%. или 102,99%.
Индивидуальный индекс показывает, что выпуск Балтики в 2003 году по сравнению с 2002 годом вырос на 4,09%, а Клинского – на 0,78%.
Индекс физического объема показывает, что в 2003 г. по сравнению с 2002 г. выпуск продукции увеличился на 2,99%.
3. Используя взаимосвязь найденных общих индексов найдем общий индекс затрат (реализации продукции).
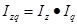
Izq=1,1513*1,0299=1,1857.
Затраты на всю продукцию выросли на 18,57%.
4. индекс себестоимости переменного состава исчисляется по формуле:
Jz
=Z1
: Z0
= 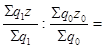 (65155/3325)/(54952/3229)=1,155. (65155/3325)/(54952/3229)=1,155.
Динамику средней cебестоимости за счет изменения структуры выпуска продукции определяется с помощью индекса изменения структуры:
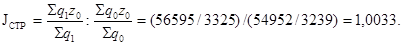 , ,
По данным приложения 2 по своему варианту
определить по плану и фактически:
1. Реализованную, чистую и условно-чистую продукцию.
2. Процент повышения плана по каждому из этих итоговых показателей. Проанализировать полученные результаты.
Таблица 12
Исходные данные
Варианты
Показатели
|
3 |
| план |
план |
| 1.Товарная продукция, млн.руб. |
15465 |
15465 |
| 2. Изменение остатков товарной продукции, млн.руб. |
| а) на складе |
+30,0 |
+30,0 |
| б) в пути |
+25,0 |
+25,0 |
| 3. Полная себестоимость товарной продукции, млн.руб. в том числе |
12372 |
12372 |
| а) материальные затраты, млн.руб. |
11260 |
11260 |
| б) оплата труда, млн.руб. |
989 |
989 |
| в) амортизация, млн.руб. |
123 |
123 |
| 4. Среднегодовая стоимость основных фондов, млн.руб. |
17776 |
17776 |
| 5. Отработано за год, тыс. чел.-дн. |
295,4 |
295,4 |
| 6. Неявки на работу, тыс. чел.-дн. |
89,7 |
89,7 |
| 7. Отработано за год, тыс. чел.-час., в том числе: |
2274,6 |
2274,6 |
| а) сверхурочные работы, тыс. чел.-час. |
- |
- |
| 8. Доля рабочих в общей численности ППП |
0,83 |
0,83 |
| 9. Прибыль, млн.руб. |
3093 |
3093 |
Решение
Реализованная продукция (РП) – отгруженная покупателям и оплаченная ими в данном периоде.
РП=ТП-(ΔТПп+ΔТПск).
План: 15465-(30+25)=15415 млн.руб.
Фактически:15795-(20+(-10)=15485 млн.руб.
Чистая продукция (ЧП) - это результат живого труда, вновь созданная стоимость за отчетный период. Она не учитывает в своем составе результаты прошлого труда и в масштабе общества представляет национальный доход (НД). Она может быть подучена двумя способами: в виде суммы оплаты труда промышленно-производственного персонала с отчислениями на социальные нужды (V) и прибыли (m), либо путем вычитания из товарной продукции затрат прошлого труда в виде стоимости материальных затрат (С)
По плану:
989+3093=4082 тыс.руб.
Фактически:
1011+3159=4170 тыс.руб.
Условно-чистая продукция (УЧП) - это чистая продукция плюс ежегодные амортизационные отчисления (А). Этот показатель в масштабе всего народного хозяйства представляет валовой национальный продукт (ВНП).
По плану
4082+123=4205 млн.руб.
Фактически
4170+126=4296 млн.руб.
Процент повышения:
- реализованной продукции: 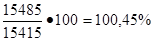 , ,
- чистой продукции: 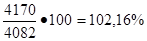
Фактически реализовано продукции по сравнению с плановым на 0,45% больше.
Фактически чистая продукция по сравнению с плановым больше на 2,16%.
По данным приложения 2 по своему варианту
определить по плану и фактически:
б) среднегодовую, среднедневную и среднечасовую выработку на одного рабочего.
3. Общее изменение товарной продукции, а также ее изменение за счет производительности труда и численности промышленно-производственного персонала по сравнению с плановым заданием.
4. Среднее число дней работы на одного рабочего.
5. Среднее число часов работы на одного рабочего.
6. Среднюю продолжительность рабочего дня (полную и урочную).
7. Показатели использования рабочего времени: коэффициент использования числа дней работы на одного рабочего; коэффициент использования продолжительности рабочего дня; полный (интегральный) коэффициент использования рабочего времени. Покажите взаимосвязь исчисленных показателей, сделайте выводы.
Решение
1) Среднемесячная численность
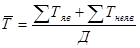
а) Среднесписочная численность ППП:
по плану
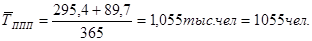
фактически
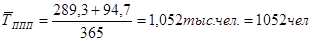
б) Доля рабочих в общей численности ППП:
по плану -0,83
фактически – 0,86
Следовательно среднесписочная численность рабочих:
по плану:
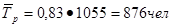
фактически:
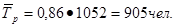
2)Показатели уровня производительности труда
а) Среднегодовая выработка на одного работника ППП:
 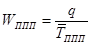
по плану
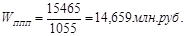
Фактически
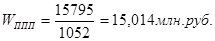
б) среднегодовая выработка на одного рабочего:
по плану:
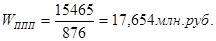
Фактически
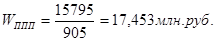
Среднечасовая выработка на одного рабочего:
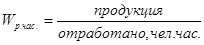
по плану
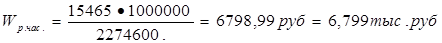
фактически
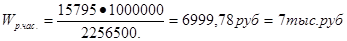
Среднедневная выработка на одного рабочего:
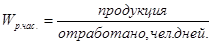
по плану
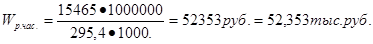
фактически
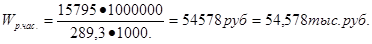
3) Общее изменение товарной продукции
Изменение объема продукции за счет изменения производительности труда и численности:
а) в относительном выражении
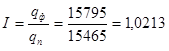 или 102,13% или 102,13%
Объем товарной продукции фактически по сравнению с планом повысился на 2,13%.
Рассмотрим из-за чего произошло увеличение.
Индекс производительности труда:
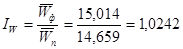 или 102,42% или 102,42%
Производительность труда фактически по сравнению с планом выросла на 2,42%
Индекс численности работников:
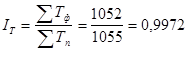 или 99,72% или 99,72%
Численность работников фактически по сравнению с планом снизилась на 0,28%.
Объем товарной продукции фактически по сравнению с планом повысился на 2,13% из-за повышения производительности труда на 2,42% и сокращения численности рабочих на 0,28%
б) в абсолютном выражении
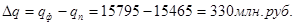
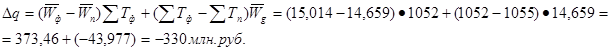
Увеличение объема товарной продукции фактически по сравнению с планом составило в абсолютном выражении 330 млн.руб. Это произошло за счет повышения производительности труда – на 274 млн.руб. и за счет сокращения численности работников на 44 млн.руб.
4). Среднее число дней работы на одного рабочего:
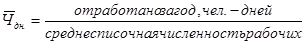
по плану
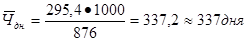
фактически:
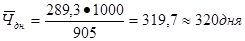
5) Среднее число часов работы на одного рабочего:
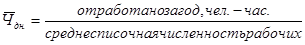
по плану
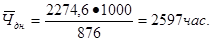
фактически:
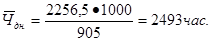
6)Средняя продолжительность рабочего дня в часах:
фактически отработанные чел.-часов
фактически отработанные чел.-дней
Различают урочную (без учета сверх урочных) и полную продолжительность рабочего дня.
Полная средняя продолжительность рабочего дня:
по плану
2274,6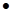 1000 1000
Дполн
=--------------- =7,7час
295,4  1000 1000
Фактически
2256,5 1000 1000
Дполн
=--------------- =7,8час
289,3 1000 1000
Урочная средняя продолжительность рабочего дня:
по плану
2274,6 1000 1000
Д=--------------- =7,7час
295,4 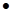 1000 1000
Фактически
(2256,5-2,5)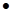 1000 1000
Д=--------------- = 7,79час
289,3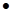 1000 1000
7) Показатели использования рабочего времени:
Коэффициент использования рабочего периода (коэффициент использования числа дней работы одного рабочего)
Среднее число дней работы
Кр.п
.=------------------------------------------
Число рабочих дней в периоде
по плану
337
Кр.п
.=---------=1,47
230
фактически:
320
Кр.п
.=---------=1,39
230
Коэффициент использования продолжительности рабочего дня:
Средняя продолжительность раб.дня в часах
Кр.д
.=----------------------------------------------------------------------------------
Средняя установленная продолжительность раб. дня в часах
Полный
-по плану
7,7
Кр.д
.=--------= 0,962
8,0
-фактически
7,8
Кр.д
.=--------= 0,975
8,0
Поурочный
-по плану
7,7
Кр.д
.=--------= 0,962
8,0
-фактически
7,79
Кр.д
.=--------= 0,974
8,0
Интегральный показатель использования рабочего времени:
Кинт
= Кр.п
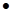 Кр.д Кр.д
полный по плану: Кинт
= 1,47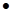 0,962 = 1,414 0,962 = 1,414
полный фактически: Кинт
= 1,39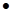 0,975 = 1,356 0,975 = 1,356
поурочный по плану: Кинт
= 1,47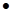 0,962 = 1,414 0,962 = 1,414
поурочный фактически: Кинт
= 1,39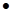 0,974 = 1,354 0,974 = 1,354
Фактически 2,6% (1-0,974) от установленной продолжительности рабочей смены недорабатывал в среднем каждый рабочий в результате недоиспользования внутрисменного времени. 0,974-0,975=-0,001-доля неиспользуемого внутрисменного времени, которая была компенсирована за счет сверхурочных работ.
На основе данных о среднегодовой, среднедневной и среднечасовой выработке на одного рабочего, а также данных о среднем числе дней работы на одного рабочего в год и средней продолжительности рабочего дня, полученных при решение задачи № 6, определите взаимосвязь всех
показателей средней выработки (производительности труда) по своему варианту
по плану и фактически. Проанализируйте полученные результаты, используя индексный факторный метод анализа (см. методические указания к решению задачи № 7).
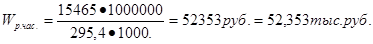
фактически
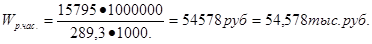
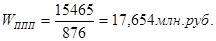
фактически
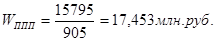
Решение
Итак, имеем данные:
среднечасовая выработка Wn
(час)
= 6,799 тыс.руб.; Wф(час)
= 7тыс.руб.
среднедневная выработка Wn
(дн)
= 52,353 тыс.руб.; Wф(дн)
= 54,578тыс.руб.
среднегодовая выработка Wn
(год)
= 17,654млн.руб.; Wф(год)
= 17,453млн.руб.
среднее число дней 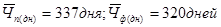
средняя продолжительность рабочего дня
Д n
(полн)
=7,7;
Д ф(полн)
=7,8.
Определим взаимосвязь всех показателей средней выработки
Wдн
= Wчас
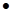 Дполн Дполн
Wп(дн)
= 6,799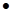 7,7 = 52,3523 тыс.руб. 7,7 = 52,3523 тыс.руб.
Wф(дн)
= 7 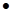 7,8 = 54,6 тыс.руб. 7,8 = 54,6 тыс.руб.
Wодн
= Wдн
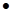 Чдн Чдн
Wп(год)
= 52,3523 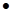 337=17642,73 тыс.руб. 337=17642,73 тыс.руб.
Wф(год)
= 54,6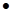 320=17472 тыс.руб. 320=17472 тыс.руб.
Неточность возникла при округлении в расчетах.
Таблица 13
Промежуточные вычисления, тыс.руб.
| показатель |
средне часовая выработка |
средняя продолжительность рабочего дня (полная) |
средняя дневная выработка |
среднее число дней работы на одного рабочего |
средняя годовая выработка на одного рабочего |
| а |
в |
a*b |
с |
v=a*b*c |
| план |
6,799 |
7,7 |
52,3523 |
337 |
17642,73 |
| фактически |
7 |
7,8 |
54,6 |
320 |
17472 |
Годовая выработка:
V=a*b*c.
Влияние факторов, обозначенных в схеме буквами а, в, с, на общее изменение среднегодовой выработки можно определить при помощи взаимосвязанных частных индексов методом цепных подстановок, поочередно принимая каждый фактор за переменную величину. Остальные факторы должны быть взяты на условно постоянном уровне.
Так, влияние фактора "а" вычисляется по формуле:
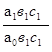 =1,0296 =1,0296
Фактора "в" по формуле:
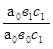 =1,0450. =1,0450.
Фактора "с" по формуле:
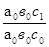 = 0,9851, = 0,9851,
что означает коэффициент динамики данного фактора.
Общее изменение среднегодовой выработки определяется по формуле:
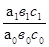 =0,9940. =0,9940.
Взаимосвязь показателей.
1,0296*1,0450*0,9851 = 0,9940.
По данным приложения 2 по своему варианту
определить по плану и фактически:
1. Показатели использования основных фондов:
а) фондоотдачу;
б) фондоемкость;
в) фондовооруженность труда;
г) затраты на один рубль товарной продукции;
д) рентабельность продукции.
2. Используя расчетные данные задачи № 6 о среднегодовой выработке одного работника ППП (среднегодовая производительность труда) и данные о фондоотдаче и фондовооруженности, покажите взаимосвязь этих показателей. Сделайте выводы.
Решение
а) фондоотдача
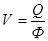
план 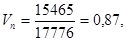
факт 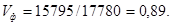
Фондоотдача по сравнению с планом увеличилась на 0,02 за счет увеличения выпуска продукции, т.е. лучшего использования оборудования.
б) фондоемкость
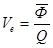
план 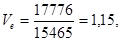
факт 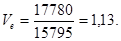
Фондоемкость – это обратный показатель фондоотдачи и снижение этого показателя по факту –это хороший показатель работы оборудования.
в) фондовооруженность труда
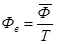
план 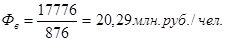
факт 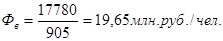
Фондовооруженность увеличилась – это говорит о поступлении нового оборудования и этот коэффициент вырос по факту в сравнении с планом на 0,03.
г) затраты на один рубль товарной продукции
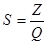
план 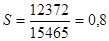
факт 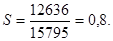
Затраты на один рубль товарной продукции остался неизменным – показывает о неизменности себестоимости продукции.
д) рентабельность продукции
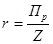
план 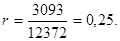
факт 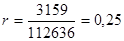
Рентабельность продукции не изменилась, что говорит о стабильности предприятия и также стабильном спросе на продукцию.
2. Взаимосвязь показателей.
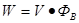 или или 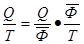
план 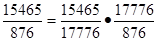
17,65=17,65.
факт 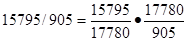
17,45=17,45.
1. Гусаров В.М. Статистика. – М.: ЮНИТИ-ДАНА, 2005.
2. Ефимова М.Р., Петрова Е.В., Румянцева В.Н. Общая теория статистики. – М.: ИНФРА-М, 2003.
3. Курс социально-экономической статистики / Под ред. М.Г. Назаровой. – М.: Финстатинформ, 2000.
4. Теория статистики / Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 1998.
|