Конкурсный урок алгебры и начала математического анализа
Тема:
"
Логарифмические уравнения
"
Класс: 11 МОУ «Гимназия №1»
Учитель: Умарова Г.К. МОУ «Кабаньевская СОШ»
Цели урока:
– организовать деятельность учащихся по изучению новой темы;
– обеспечить закрепление новых понятий логарифмическое уравнение, методы решения логарифмических уравнений;
– научить учащихся решать логарифмические уравнения методом, основанным на определению логарифма, методом потенцирования;
– развивать умение анализировать, сопоставлять, делать выводы, синтезировать полученные знания и умения;
– воспитывать умение работать в парах; навык самооценки и взаимооценки.
Оборудование: мультимедийный проектор
Ход урока:
Дорогие ребята! Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением: Математика – интересный и очень нужный предмет. Наш урок я назвала уроком Красоты и гармонии. В вашем понимании, что такое красота? Что такое гармония?
Душой математики является красота и гармония. Я хочу, чтобы вы чувствовали эту красоту, и это чувство помогало вам в изучении такого замечательного предмета, как математика. О гармонии в математики, о ее красоте говорили очень многие. Об этом говорил и известный академик-геометр 20 века Александр Данилович Александров. Его слова является эпиграфом нашего урока:
Холодные числа, внешне сухие формулы математики полны внутренней красоты и жара сконцентрированной в них мысли.
Александров А.Д.
Эти слова я бы полностью отнесла к теме, которую мы с вами рассматриваем сегодня.
Устная работа
1. Вычислите устно:
а) log28
б) lg 0,01;
в) 2 log 2
32.
Что использовали для выполнения данного задания? (определение логарифма)
2. Найдите х:
а) log3
x = 4 (х=81)
б)) log3
(7х-9)=log3
x (х= 1,5)
Как иначе сформулировать 3 задание? (решите уравнение)
А как вы думаете, какие это уравнения? (логарифмические)
Запишем тему урока: «Логарифмические уравнения»
Давайте сформулируем цели урока.
Можете сформулировать определение логарифмического уравнения?
Объяснение нового материала
Записать
на доске, поясняя
log аf(x) = log ag(x), где а-положит. число, отличное от 1, и уравнения, сводящиеся к этому виду.
Посмотрим, как вы нашли корень 1 уравнения
Чем пользовались? (определением)
Итак, выделим первый метод решения логарифмических уравнений, основанный на определении логарифма.
Общий вид такого уравнения 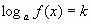 . Это уравнение может быть заменено равносильным ему уравнением . Это уравнение может быть заменено равносильным ему уравнением 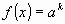 . .
Давайте оформим решение уравнения 2.
log3
(7x – 9) = log3
x
7х – 9 = х
6х = 9
х = 1,5
Применение формул потенцирования расширяет область определения уравнения. Поэтому необходима проверка корней. Проверим найденные корни по условиям 7х-9>0
x>0
Для решения данного уравнения мы использовали метод потенцирования. Этот метод применяется для уравнений вида 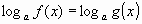 и сводится к решению уравнения f(x)=g(x), х должен удовлетворять решению системы. и сводится к решению уравнения f(x)=g(x), х должен удовлетворять решению системы.
Мы рассмотрели с вами 2 метода решения логарифмических уравнений. Какие? (по определению, метод потенцирования)
Закрепление
№17.1 устно
Каким методом будем находить корень уравнения? (по определению)
А) 8 б) 1/7 в) 0,09 г.) 4
№17 (а, б) с комментированием. Каким методом будем решать?
А) log0,1
(x2
+4x-20)=0 б) log1/7
(x2
+x-5)= – 1
x2
+4x-20=0,10
x2
+x-5=1/7 – 1
x2
+4x-20=1 x2
+x-5=7
x2
+4x-21=0 x2
+x-12=0
x1
+x2
= -4 x1
+x2
= -1
x1
*x2
=-21 x1
*x2
=-12
x1
=-7, x2
= 3 x1
=-4, x2
= 3
№17.6 (а, б)
Каким методом будем решать? (потенцирования)
Решаем в парах
А) 3х-6=2х-3 б) 14+4х=2х+2
3х-2х=-3+6 4х-2х=2–14
х=3 2х= – 12, х= – 6. корней нет
Самостоятельная работа
Вам предложены уравнения. Ваша задача решить эти уравнения и соотнести ответы с соответствующей буквой. В результате должно получиться слово. Обращаю ваше внимание, что уравнения взяты из демоверсий ЕГЭ, задание В3.
1. 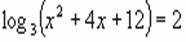 (-1, – 3) (-1, – 3)
2. 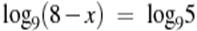 (х=3) (х=3)
3. 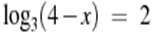 (х=-5) (х=-5)
4. 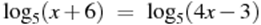 (х=3) (х=3)
5. 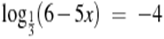 (х=-15) (х=-15)
Ключ
| 3
|
-2
|
-3, – 1
|
-15
|
-7
|
-1
|
-5
|
0
|
12
|
| Е
|
А
|
Н
|
Р
|
Д
|
О
|
П
|
З
|
Л
|
Джон Непер
Графический диктант
А сейчас вы побудете в роли учителя. Вам необходимо определить верно ли найдены корни уравнения. Если верно вы рисуете
«да» – ^, «нет» – Выписываете свой фигуры в одну строчку.
| В-1 |
В-2 |
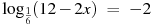 , х = – 12 , х = – 12 |
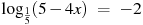 , х = 5 , х = 5 |
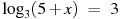 , х= – 22 , х= – 22 |
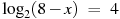 , х = – 8 , х = – 8 |
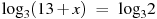 , х = – 11 , х = – 11 |
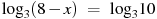 , х = – 2 , х = – 2 |
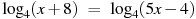 , х = 3 , х = 3 |
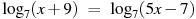 , х = – 4 , х = – 4 |
Ответы:
^-^^ -^^-
Итог урока:
Сейчас мы сдадим мини экзамен по теме нашего урока.
Билеты:
1. Дайте определение логарифмического уравнения.
2. Какими методами можно решать логарифмические уравнения?
3.
4.
5.
6.
Считаете ли вы, что цели урока решены? Чему научились, что закрепили?
На партах у вас есть кружки голубого, оранжевого и розового цвета. Оцените себя за деятельность на уроке. 3-гол цвет, 4 – оранжевый, 5 – розовый.
Домашнее задание.
Возьмите карточки с разноуровневым дом задание. Кто желает может взять все уровни.
1 уровень
· log 3
x= 4
· log 2
x= -6
· logx
64 = 6
· – log x
64 = 3
· 2 log x
8 + 3 = 0
2 уровень
· log 3
(2х – 1) = log 3
27
· log 3
(4х+5)+log 3
(х +2) = log 3
(2х +3)
· log 2
х = – log 2
(6х – 1)
· 4 + log 3
(3-х) = log 3
(135–27х)
· log (х – 2) + log 3
(х – 2) = 10
(х – 2) + log 3
(х – 2) = 10
3 уровень
· 2log 2
3
х – 7 log 3
х + 3 = 0
· lg 2
х – 3 lg х – 4 = 0
· log 2
3
х – log 3
х – 3 = 2 lоg
2
3
В заключении урока я хочу вам прочитать стихотворение:
«Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,а математика способна достичь всех этих целей».
Так сказал американский математик Морис Клайн.
Спасибо за работу!
логарифмический решение уравнение урок
|