Контрольная работа
«Вещественные числа: способы представления и хранения в ЭВМ»
Рязань, 2006 г.
1. Цель работы
1. Изучение основных типов данных с плавающей точкой, принятых стандартов и их представление в современных ЭВМ.
2. Наработка практических навыков обращения с вещественными числами на компьютере (запись, считывание, хранение).
2. Теоретическая часть
2.1 Вещественные числа
Вещественные числа (REAL) – числа, имеющие дробную часть. Для их представления в компьютере используется так называемое представление с плавающей точкой (ПТ), основанное на алгебраической записи чисел в виде:
X = ±Mx
q±Пх
плавающий вещественный число компьютер
где q – основание системы счисления;
Пх
– порядок числа (целое);
Мх
– мантисса (значащая часть числа), обычно представляется дробью:
Mx= ±0.d1
d2
… dn
.
Условие di
≠0 является характерным признаком нормализованного числа в ФПТ. Нормализованное представление используется для однозначной записи вещественных чисел. Для нормализованной двоичной мантиссы (q=2) диапазон определяется неравенством 2-1
≤ |Мх| <1. Знак числа определяется знаком мантиссы.
Мантисса числа X в общем виде записывается соответственно как
а) Мх =.d0
d1
d2
d3
d4
, где di
{0,1};
б) Мх = d0
.d1
d2
d3
d4
, где di
{0,1}.
Разряд d0
в нормализованных числах всегда равен «1» и в памяти компьютера не хранится («скрытый бит»). Таким образом, мантисса, хранящаяся в памяти компьютера всегда число дробное. (Рис. 1)
d1 d2 d3 d4…
↑ ↑
«скрытый» бит место точки
Рис. 1. Представление n-разрядной мантиссы
Форма представления чисел с ПТ позволяет значительно увеличить диапазон и точность представления чисел при той же длине разрядной сетки что и для чисел с ФТ.
2.2 Представление в памяти
Вещественные числа в отличие от целых представляются и хранятся в памяти в прямом коде, их представление стандартизовано. Согласно стандарту IEЕЕ – 754 для ПК IBМ PC вводят три машинных формата:
– одинарной точности (4 байта);
– двойной точности (8 байт);
– расширенной точности (10 байт).
Некоторые фирмы разработчики ПО используют нестандартные форматы (в компиляторе языка Pascal фирмы Borland используется формат длиной б байтов).
Представление вещественных чисел в классическом двоичном формате
Представление вещественных чисел в классическом двоичном формате имеет четыре поля используется в старых ЭВМ.
Задание 1. Считать из памяти (найти Х10
) число, представленное в классическом двоичном формате.
X= -0.10100*2-3
= -19/32*2-3
= -19/256.
Задание 2 Х= +7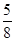 представить в классическом двоичном формате (n=5, m=3). X= +7 представить в классическом двоичном формате (n=5, m=3). X= +7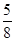 = 111.1012
= 0.111101*2+3 = 111.1012
= 0.111101*2+3
0 11110 0 0112
2.3 Машинные форматы вещественных данных
В различных алгоритмических языках принятые стандарты описываются разными ключевыми словами.
В языке Turbo-Pascal определены следующие типы вещественных чисел: single, Real, double, extended и comp.
Типы вещественных чисел в языке Turbo-Pascal приведены в таблице 1.
Таблица 1. Типы вещественных чисел в языке Turbo-Pascal
| Название типа |
Длина в байтах |
Мантисса (десятичных значащих цифр) |
Диапазон десятичного порядка |
| single |
4 |
7… 8 |
-45..+38 |
| real |
б |
11…12 |
-39..+38 |
| double |
8 |
15…16 |
-324..+308 |
Во всех типах мантисса хранится в прямом коде (ПК). Порядок (или экспонента е) задается в так называемой смещенной форме. Смещение выбирается так, чтобы характеристика была целым положительным числом (тогда знак характеристики хранить не требуется).
Смещение для типа real =129, для типа single =127, для типа double =1023.
Смещенный порядок (характеристика Е) равен истинному порядку П, увеличенному на величину смещения, т.е. Е=П+смещение.
Если 0<Е<255, то значение числа X определяется по правилу:
дляформат single: X = f (S, E, M) = (-l)S
-2(E -l27)
(1.M);
дляформата real: X = f (S, M, E) = (-l)S
-2(E -l29)
(1.M), где S=0 или 1.
2.4 Внутреннее представление вещественных данных
Формат Single (4 байта)
31 30 23 22 0
если 0<E<255, то (-1)s
*2(
E
-127)
*(1.M)
если E=0 и M≠255, то (-1)s
*2(
E
-127)
*(1.M)
1. X= f (S, E, M) = если E=0 и M=0, то (-1)s
*0
если E=255 и M=0, то (-1)s
*∞
если E=255 и M≠0, то X-нечисло (NAN, Not-a-Number).
Формат real (6 байт)
47 46 8 7 0
0, если е=0
Х = f(S, M, E) =
(-1)S
*2(
E
-129)
*(1.М), если 0<Е<255
Формат double (8 байтов)
63 62 52 51 0
Х = (-1)s
*2(
E
-01023)
*(1.M).
3. Практическая часть
Считывание вещественных чисел из памяти ЭВМ.
Регистрация:
– выбрать пункт меню «Информатика»;
– в появившемся подменю выбрать пункт GR440;
– после появления приглашения D:\INFORM\GR440 запустить рабочую среду, набрав на клавиатуре Lab6 и нажав [Enter].
Задание 1.
Число -23 представить в ФПТ в форматах single, real и double и разместить в памяти ПК, начиная с адреса ds: OOCOh. Результаты преобразования и перехода от значения числа к представлению его в памяти занести в таблицу 2.
Таблица 2. Переход от X10
к отображению в памяти
| Число |
Алгебраическая запись |
Формат |
16-ричное представление числа |
Адрес |
Отображение в памяти |
| -23 |
-1.0111*2+4
|
single |
С1 B8 00 00 |
ds:00C0h |
00 00 B8 C1 |
| -23 |
-1.0111*2+4
|
real |
B800 00 00 00 85 |
ds:00C8h |
85 00 00 00 00 B8 |
| -23 |
-1.0111*2+4
|
double |
C0 37 00 00 00 00 00 00 |
ds:00D0h |
00 00 00 00 00 00 37 C0 |
Комментарии к таблице 2:
Х=-23=-1.01112
=-1.0111*2+4
В формате single:
порядок Е=4+127=131=83h=100000112
SgEM
Х: 1 10000011 01110000000000000000000
Х: 1100 0001 1011 1000 0000 0000 0000 0000
Х: C1 B8 0 0 0 0
Число Х=-23 в формате single в 16-ричной СС представляется как Х:С1В80000h и отображается в памяти в обратном порядке Х:00 00 В8 С1.
В формате real:
порядок Е=4+129=133=85h=100001012
SgME
Х: 1 011100000000000000000000000000000000000 10000101
Х: 1011 1000 0000 0000 0000 0000 0000 0000 0000 0000 1000 0101
Х: B8 0 0 0 0 0 0 0 0 8 5
Число Х=-23 в формате real в 16-ричной СС представляется как Х:В80000000085h и отображается в памяти в обратном порядке Х:85 00 00 00 00 В8.
В формате double:
порядок E=4+1023=1027=403h=100000000112
SgEM
Х: 1 10000000011 0111000000000000000000000000000000000000000000000000
Х: 1100 0000 0011 0111 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Х: C0 3 7 0 0 0 0 0 0 0 0 0 0 0 0
Число Х=-23 в формате double в 16-ричной СС представляется как Х:С037000000000000h и отображается в памяти в обратном порядке Х:00 00 00 00 00 00 37 С0.
Задание 2.
По адресам ds:2h, ds:2ah, ds:66h считать из памяти числа, в режиме отображения byte, представленные в форматах single, real и double, и найти их десятичный эквивалент. Результаты представить в виде таблицы 3.
Вариант 8 (адреса:
ds
:1
Eh
,
ds
:54
h
,
ds
:9
Eh
)
Установить подокно с отображением оперативной памяти (ОП) на область, начинающуюся с адреса ds:1Eh:
– Ctrl+G;
– В открывшемся диалоговом окне набрать адрес ds:1Eh и нажать <Enter>;
Установить режим отображения byte, после чего нажать <Enter>;
– ALT+F10;
– Переместите курсор на пункт Displayas и нажмите <Enter>;
– Выберите требуемый режим отображения (byte) и нажмите <Enter>;
– Перенести представление числа в памяти, расположенного по адресу ds:1Eh, в Таблицу 2.
Установить подокно с отображением оперативной памяти (ОП) на область, начинающуюся с адреса ds:54h:
– Ctrl+G;
– В открывшемся диалоговом окне набрать адрес ds:54h и нажать <Enter>;
– Перенести представление числа в памяти, расположенного по адресу ds:1Eh, в Таблицу 2.
Установить подокно с отображением оперативной памяти (ОП) на область, начинающуюся с адреса ds:9Eh:
– Ctrl+G;
– В открывшемся диалоговом окне набрать адрес ds:9Eh и нажать <Enter>;
– Перенести представление числа в памяти, расположенного по адресу ds:1Eh, в Таблицу 3.
Таблица 3. Переход от отображения в памяти к Х10
| Адрес |
Формат |
| ds:0002h |
single |
| ds:002аh |
real |
| ds:0066h |
double |
Список литературы
1. Информатика, ч.I: Методические указания к лабораторным работам / Сост. Н.И. Иопа. – Рязань: РГРТА 2002.
2. Информатика. Базовый курс / С.В. Симонович и др. СПб.: Питер, 2001, с. 114–120.
3. Шафрин Ю.А. Информационные технологии. М.: Лаборатория Базовых знаний, 1998, с. 164–179.
|