Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Омский государственный технический университет
Кафедра: "Средства связи и информационная безопасность"
Курсовая работа по дисциплине "Основы Теории Цепей"
Тема проекта:
Синтез и анализ электрического фильтра
Выполнил студент:
Кузюков Виктор Васильевич
Группа: ЗРП-218 (210402)
Проверил преподаватель:
Омск 2010 г.
Исходные данные
| Тип фильтра |
Amin
(дБ) |
∆A (дБ) |
Rг
, Rн
(Ом) |
f0
(кГц) |
Кпр
|
| НЧ |
55 |
1,5 |
3,0 |
180 |
2,5 |
1) Тип фильтра – НЧ (низкочастотный)
2) Минимально-допустимое значение рабочего ослабления в ПЗ Amin
- 55 дБ
3) Неравномерность затухания в полосе пропускания ∆A - 1,5 дБ
4) Сопротивление генератора и нагрузки Rг
, Rн
- 3,0 Ом
5) Частота полосы пропускания f0
– 180 кГц
6) Коэффициент пропускания (Кпр
= ПЗ / ПП) Кпр
– 2,5
Для создания электрического фильтра надо выбрать Аппроксимирующий полином:
Я для работы выбрал Аппроксимирующий полином — Баттерворта. Расчёты для фильтра 5-го порядка.
Фильтрами НЧ (ФНЧ) называют фильтры, пропускающие в нагрузку лишь низкие частоты: с ω1
= 0 до ω2
. Полоса их затухания находится в интервале от ω2
до ∞.
Фильтры НЧ можно классифицировать в зависимости от их характеристик. Характеристика затухания фильтра Баттерворта приведена на рис.1. Фильтр Баттерворта характеризуется монотонным изменением затухания в полосе пропускания и задерживания. Затухание в полосе задерживания (ПЗ) изменяется приблизительно на 6 дБ за октаву для каждого элемента схемы. Например, пятиэлементный фильтр будет иметь затухание 30 дБ при двойной частоте среза и 60 дБ при учетверенной частоте среза. За нормированную частоту Ω = l для фильтра Баттеворта принимается частота, на которой затухание составляет 3 дБ.
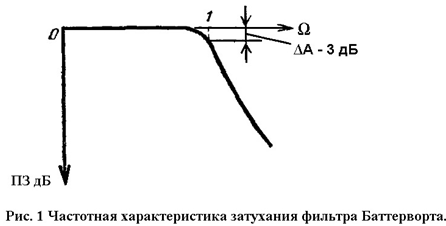
Нормирование.
На практике обычно величины элементов фильтра нормируются для частоты среза 1 рад/с при сопротивлении нагрузки 1 Ом. Для преобразования нормированных величин в реальные их необходимо умножить на коэффициент преобразования. Например, нормированная индуктивность и емкость умножаются на постоянные КL
и КC
, которые можно вычислить с помощью следующих формул:

где R - сопротивление нагрузки;  - частота среза; все величины выражены в генри, фарадах, омах и герцах. - частота среза; все величины выражены в генри, фарадах, омах и герцах.
Приведенные формулы можно преобразовать в одну дискретным выбором единиц. Если используется сопротивление, равное 1000 Ом, частота среза выражена в килогерцах, а постоянные KL
и КC
- в микрогенри и пикофарадах, формула приводится к виду

Для расчёта фильтра далее будут использоваться спец. таблицы в которых применяется следующее сокращённые обозначение:
B02 – фильтр Баттерворта 2-го порядка.
G03 – фильтр Гаусса 3-го порядка.
Т05-10 – фильтр Чебышева 5-го порядка с максимальным коэффициентом отражения 10%
С07-20-38 – фильтр Крауэра 7-го порядка с максимальным коэффициентом отражения 20% и модульным углом 38º
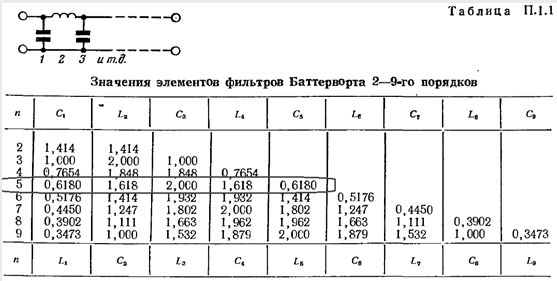
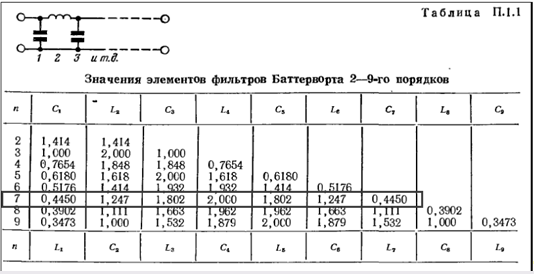
Нормированные значения элементов для фильтра Баттерворта приводятся в табл. П. 1.1. Требуемые значения элементов получаются в результате умножения нормированных значений на постоянную преобразования.
По вышеуказанным формулам рассчитываю значения для KL
иKC
KL
= 3 / (2 * 3,14 * 180000) = 2,65*10-6
Гн.
KC
= 1 / (2 * 3,14 * 180000 * 3) = 2,95*10-7
Ф.
Далее находим значения C1
, L2
, C3
, L4
, C5
C1
= 0,618 * 2,95*10-7
= 1,8231*10-7
Ф
L2
= 1,618 * 2,65*10-6
= 4,2877*10-6
Гн
C3
= 2,000 * 2,95*10-7
= 5,9000*10-7
Ф
L4
= 1,618 * 2,65*10-6
= 4,2877*10-6
Гн
C5
= 0,618 * 2,95*10-7
= 1,8231*10-7
Ф
Для проверки работы фильтра я использовал программное обеспечение MicroCap 7.
Построив схему фильтра НЧ по подобию из таблице П.1.1 и добавив учтённые сопротивления генератора и нагрузки, получается "идеальный" фильтр.

Здесь под "идеальным" я предполагаю что у нас будут характеристики фильтра с найденными значениями, но в реальных условиях приходится подбирать номиналы из стандарта рядов номиналов выпускаемых радиоэлементах. (Возможно можно заказать индивидуально выпуск штучно под устройство, но это делается для особых случаев, в нашем случае это нецелесообразно) Более подробно о рядах в приложении, для начала проведём анализ построенного фильтра, посмотрим его амплитудночастотную характеристику (АЧХ) и фазавочастотную характеристику (ФЧХ).
Для анализа выбираем Analysis – AC…
В раскрывшемся окне "ACAnalysisLimits"
для просмотра АЧХ надо ввести db (v(Out)),
для просмотра ФЧХ надо ввести ph(v(Out)).
Остальные параметры устанавливаются для каждого отдельного случая. В моём анализируется участок от 50 кГц до 1 мГц в одном окне.

Дополнительно включаем AutoScalrRanges и жмём Run и получаем график.
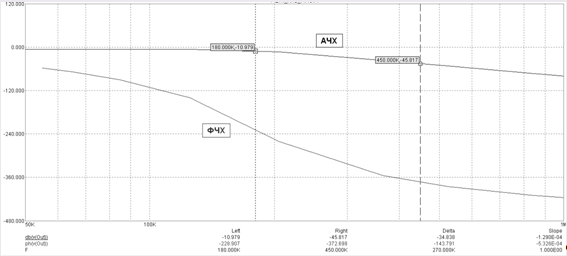
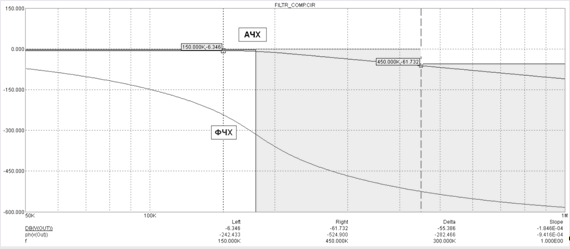
где что в ПП проходят частоты до 180 кГц и далее начинается спад. Из данных выше зная что коэффициент пропускания Кпр
= ПЗ / ПП = 2,5. ПП = 180 кГц, находится ПЗ = Кпр
* ПП откуда и получаем 180 * 2,5 = 450 кГц.
Проверим проходную способность выбрав AnalysisTransient…и для примера подадим на вход 3 разных частоты по отдельности с шагом в 170 кГц. (170, 340,510)
Для этого изменим частоту входного сигнала, для каждого случая:

Далее выбираю AnalysisTransient… и ввожу следующие характеристики анализа:

При этом далее видим:

На граф. анализе, не вдаваясь в детали запаздывание фазы и группового время запаздывания, видно что фильтр пропускает частоту 170 кГц.
Далее провожу те же операции, но на вход подаю следующее экспериментальное значение – 340 кГц., при этом частота уже попадает в ПЗ и её уровень амплитуды должен уменьшаться.


По графику видно затухание происходит.
И то же самое для частоты - 510 кГц., где амплитуда частоты должна быть приближённой к нулю.


Как видим получилось, что фильтр работает.
Для проверки или постройки фильтра в среде MicroCap можно использовать встроенную функцию, выбрав меню Design и выбрать фильтр для построения Активного или Пассивного фильтра, в моём случае выбираю PassiveFilters… В окне PassiveFilters Designer ввожу данные, при этом выбираю фильтр Баттерворта, в программе он 7 порядка


После ввода значений получаем схему:

Для проверки сравню полученные данные с теми которые считал выше для фильра 5-го порядка сделав расчёт на примере C1 и L1 построенной схемы для 7-го найдя расчётные C1р
и L1р
. По схеме:
C1 = 131,1678 * 10-9
Ф
L1 = 3,30772 * 10-6
Гн
Рассчитаем.
KL
= 3 / (2 * 3,14 * 180000) = 2,65*10-6
Гн.
KC
= 1 / (2 * 3,14 * 180000 * 3) = 2,95*10-7
Ф.
Тогда:
C1р
должно быть 0,4450 * 2,95*10-7
= 1,31278*10-7
или 131,278*10-9
Ф
L1р
должно быть 1,247 * 2,65*10-6
= 3,30455*10-6
Гн
Сравним полученные результаты:
| C1 Ф |
C1р
Ф |
L1 Гн |
L1р
Гн |
| 131,1678 * 10-9
|
131,278*10-9
|
3,30772 * 10-6
|
3,30455*10-6
|
| 131,1678 * 10-9
- 131,278*10-9
|
3,30772 * 10-6
- 3,30455*10-6
|
| Разница по модулю = 1,1*10-10
|
Разница по модулю = 2,6222*10-7
|
Разница не значительная, учитывая при этом что реальный состав компонентов к фильтру будем подбирать по раду номиналов.
Просмотрим анализ.
Проверим на фильтрацию тестовых частот 170, 340,510 кГц.
На частоте 170 кГц.
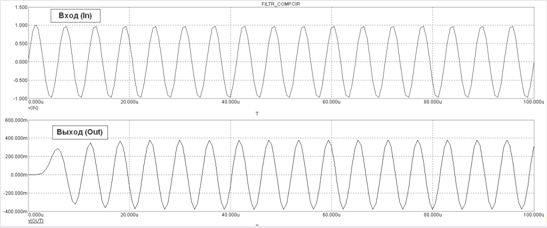
На частоте 340 кГц
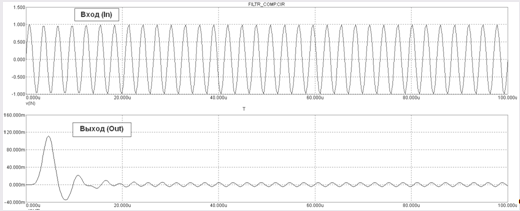
На частоте 510 кГц

Из проведённой проверки видно, что мой фильтр работает практически идентично построенному автоматически. Расхождение и более грубая характеристика моего фильтра по сравнению с программным объясняется не точностью вычислений при расчёте и учёте малой разрядности (если у меня вычисления с точностью до трёх знаков, после запятой, то компьютер считает с гораздо большей разрядностью и фильтр берется на 2 порядка выше).
Теперь из рассчитанной ранее схемы:

Составляю реальную схему выбрав значения из ряда номиналов радиодеталей из ряда E6, E12, E24:


Получим:
аппроксимирующий электрический фильтр радиодеталь
| Расчётные данные |
Из соотв. Ряда E6,E12,E24 |
| C1
= 1,8231*10-7
Ф |
1,8*10-7
Ф |
| L2
= 4,2877*10-6
Гн |
4,3*10-6
Гн |
| C3
= 5,9000*10-7
Ф |
5,6*10-7
Ф |
| L4
= 4,2877*10-6
Гн |
4,3*10-6
Гн |
| C5
= 1,8231*10-7
Ф |
1,8*10-7
Ф |

Полученную схему анализирую подобно расчётной и получаю данные:

По тесту на пропускания:
На частоте 170 кГц

На частоте 340 кГц

На частоте 510 кГц

Приложение
Ряды номиналов радиодеталей
Номиналы промышленно выпускаемых радиодеталей (сопротивление резисторов, ёмкость конденсаторов, индуктивность небольших катушек индуктивности) имеют отнюдь не произвольные значения, а берутся из специальных номинальных рядов. Точнее, номиналы деталей могут быть произвольным числом из соответствующего ряда, умноженным на произвольный десятичный множитель (десять в произвольной степени), например резистор из ряда E12 может иметь сопротивление 1,2 Ом, 12 Ом, 120 Ом, …, 1,2 МОм, 12 МОм, 1,5 Ом, 15 Ом и т. д.
Номинальные ряды E6, E12, E24
Название ряда указывает общее число элементов в нём, т. е. ряд E24 содержит 24 числа в интервале от 1 до 10, E12 — 12 чисел и т. д.
Каждый ряд соответствует определённому допуску в номиналах деталей. Так, детали из ряда E6 имеют допустимое отклонение от номинала ±20 %, из ряда E12 — ±10 %, из ряда E24 — ±5 %. Собственно, ряды устроены таким образом, что следующее значение отличается от предыдущего чуть меньше, чем на двойной допуск.
Указание на схемах номиналов элементов, не принадлежащих никакому ряду без особого технического обоснования, считается неграмотностью. Поэтому хорошие радиоинженеры помнят ряд E24 наизусть. Значения номиналов для некоторых рядов приведены в таблице:

Видно, что ряд E12 получается вычёркиванием из ряда E24 каждого второго номинала, аналогично, E6 получается вычёркиванием из E12 каждого второго номинала.
Простая формула для получения значений номиналов:
V(n) = Round(100*exp((n-1)/N*ln(10))),
где V(n) значение n-го номинала в классе E-N (N=192,96,48,24,12,6,3).
Принципы построения рядов
Ряд E24 приблизительно представляет собой геометрическую прогрессию со знаменателем 101/24. Другими словами, в логарифмическом масштабе элементы этого ряда делят отрезок от 1 до 10 на 24 равные части. По некоторым, видимо историческим, соображениям некоторые элементы отличаются от идеальной прогрессии, хотя и никогда не больше, чем на 2,5 %. Номинальные ряды с меньшим количеством элементов получаются вычёркиванием элементов из ряда E24 через один. Номиналы из этих рядов образуют примерно геометрическую прогрессию со знаменателем 101/12 (E12), 101/6 (E6), 101/3 (E3). Ряд E3 практически не применяется. Номинальные ряды с большим числом элементов образуют уже абсолютно точную геометрическую прогрессию со знаменателем 101/n, где n — число элементов ряда. Число n всегда представляет собой степень двойки, умноженную на 3.
Номинальный ряд по сути своей представляет собой таблицу десятичных логарифмов. Действительно, порядковый номер элемента в ряду минус 1 даёт мантиссу логарифма в виде простой дроби со знаменателем (m − 1)/n (m — номер элемента, n — порядок ряда, например, 24 для E24). Зная наизусть ряд E24, можно, таким образом, в уме вычислять произведения чисел, корни небольших степеней из чисел, логарифмы чисел с точностью, примерно ±5 %. Например, вычислим квадратный корень из 1000. Десятичный логарифм этого числа равен 3, поделив его пополам, находим, что десятичный логарифм ответа 1,5 = 1 + 12/24, т. е. ответ есть 10 умноженное на элемент, стоящий в ряду E24 на 13-м месте, т. е. точно в середине ряда, т. е. получили примерно 33.
Есть универсальный способ определения номинала для любого ряда V(n)=(10^n)^(1/m), где m - номер ряда, а n=0;1;2;...;m-1. (Бодиловский В.Г., Смирнов М.А. Справочник молодого радиста. Изд. 3-е. перераб. и доп. М, "Высш. школа", 1976)
Номинальные ряды с большим числом элементов
Ряд E48 соответствует относительной точности ±2 %, E96 — ±1 %, E192 — ±0,5 %. Хотя элементы этих рядов образуют строгую геометрическую прогрессию со знаменателями 101/48 ≈ 1,04914, 101/96 ≈ 1,024275, 101/192 ≈ 1,01206483 и легко могут быть вычислены на калькуляторе, тем не менее для удобства приведём и эти ряды.
Номинальные ряды E48, E96, E192

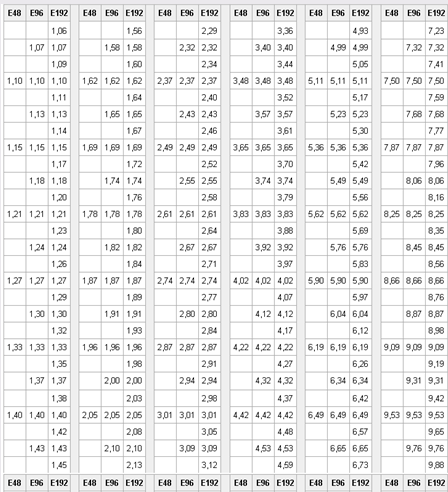
Библиографический список
1. Ханзел. Г.Е., Справочник по расчёту фильтров. США, 1966, Пер. с англ., В.А.Старостина, под ред. А.Е.Знаменского. М., "Сов. радио" 1974 г. 288 с. С ил.
2. Internet: Ряды номиналов радиодеталей http://ru.wikipedia.org/wiki/E96
|