МОДЕЛИРОВАНИЕ СЕТИ КЛАСТЕРИЗАЦИИ ДАННЫХ В MATLAB NEURAL NETWORK TOOL
СОДЕРЖАНИЕ
Введение
1. Общие сведения о кластеризации
1.1 Понятие кластеризации
1.2 Процесс кластеризации
1.3 Алгоритмы кластеризации
1.3.1 Иерархические алгоритмы
1.3.2 k-Means алгоритм
1.3.3 Минимальное покрывающее дерево
1.3.4 Метод ближайшего соседа
1.3.5 Алгоритм нечеткой кластеризации
1.3.6 Применение нейронных сетей
1.3.7 Генетические алгоритмы
1.4 Применение кластеризации
2. Сеть Кохонена
2.1 Структура сети Кохонена
2.2 Обучение сети Кохонена
2.3 Выбор функции «соседства»
2.4 Карта Кохонена
2.5 Задачи, решаемые при помощи карт Кохонена
3. Моделирование сети кластеризации данных в MATLABNEURALNETWORKTOOLBOX
3.1 Самоорганизующиеся нейронные сети в MATLABNNT
3.1.1 Архитектура сети
3.1.2 Создание сети
3.1.3 Правило обучения слоя Кохонена
3.1.4 Правило настройки смещений
3.1.5 Обучение сети
3.1.6 Моделирование кластеризации данных
3.2 Карта Кохонена в MATLABNNT
3.2.1 Топология карты
3.2.2 Функции для расчета расстояний
3.2.3 Архитектура сети
3.2.4 Создание сети
3.2.5 Обучение сети
3.2.6 Моделирование одномерной карты Кохонена
3.2.7 Моделирование двумерной карты Кохонена
Выводы
Перечень ссылок
ВВЕДЕНИЕ
В настоящее время ни у кого не вызывает удивления проникновение компьютеров практически во все сферы человеческой деятельности. Совершенствование элементной базы, определяющей архитектуру компьютера, и распараллеливания вычислений позволяют быстро и эффективно решать задачи все возрастающей сложности. Решение многих проблем немыслимо без применения компьютеров. Однако, обладая огромным быстродействием, компьютер часто не в состоянии справиться с поставленной перед ним задачей так, как бы это сделал человек. Примерами таких задач могут быть задачи распознавания, понимания речи и текста, написанного от руки, и многие другие. Таким образом, сеть нейронов, образующая человеческий мозг, являясь, как и компьютерная сеть, системой параллельной обработки информации, во многих случаях оказывается более эффективной. Идея перехода от обработки заложенным в компьютер алгоритмом некоторых формализованных знаний к реализации в нем свойственных человеку приемов обработки информации привели к появлению искусственных нейронных сетей (ИНС).
Отличительной особенностью биологических систем является адаптация, благодаря которой такие системы в процессе обучения развиваются и приобретают новые свойства. Как и биологические нейронные сети, ИНС состоят из связанных между собой элементов, искусственных нейронов, функциональные возможности которых в той или иной степени соответствуют элементарным функциям биологического нейрона. Как и биологический прототип, ИНС обладает следующим свойствами:
·адаптивное обучение;
·самоорганизация;
·вычисления в реальном времени;
·устойчивость к сбоям.
Таким образом, можно выделить ряд преимуществ использования нейронных сетей:
·возможно построение удовлетворительной модели на нейронных сетях даже в условиях неполноты данных;
·искусственные нейронные сети легко работают в распределенных системах с большой параллелизацией в силу своей природы;
·поскольку искусственные нейронные сети подстраивают свои весовые коэффициенты, основываясь на исходных данных, это помогает сделать выбор значимых характеристик менее субъективным.
Сейчас мир переполнен различными данными и информацией - прогнозами погод, процентами продаж, финансовыми показателями и массой других. Часто возникают задачи анализа данных, которые с трудом можно представить в математической числовой форме. Например, когда нужно извлечь данные, принципы отбора которых заданы нечетко: выделить надежных партнеров, определить перспективный товар, проверить кредитоспособность клиентов или надежность банков и т.п. И для того, чтобы получить максимально точные результаты решения этих задач необходимо использовать различные методы анализа данных. В частности, можно использовать ИНС для кластеризации данных, что, на мой взгляд является наиболее перспективным подходом.
1.ОБЩИЕ СВЕДЕНИЯ О КЛАСТЕРИЗАЦИИ
1.1 Понятие кластеризации
Классификация– наиболее простая и распространенная задача. В результате решения задачи классификации обнаруживаются признаки, которые характеризуют группы объектов исследуемого набора данных - классы; по этим признакам новый объект можно отнести к тому или иному классу.
Кластеризация – это автоматическое разбиение элементов некоторого множества на группы в зависимости от их схожести. Синонимами термина "кластеризация" являются "автоматическая классификация", "обучение без учителя" и "таксономия".
Задача кластеризации сходна с задачей классификации, является ее логическим продолжением, но ее отличие в том, что классы изучаемого набора данных заранее не предопределены. Таким образом кластеризация предназначена для разбиения совокупности объектов на однородные группы (кластеры или классы). Если данные выборки представить как точки в признаковом пространстве, то задача кластеризации сводится к определению "сгущений точек".
Целью кластеризации является поиск существующих структур.
Кластеризация является описательной процедурой, она не делает никаких статистических выводов, но дает возможность провести разведочный анализ и изучить "структуру данных".
Само понятие "кластер" определено неоднозначно: в каждом исследовании свои "кластеры". Переводится понятие кластер как "скопление", "гроздь". В искусственных нейронных сетях под понятием кластер понимается подмножество «близких друг к другу» объектов из множества векторов характеристик. Следовательно, кластер можно охарактеризовать как группу объектов, имеющих общие свойства.
Характеристиками кластера можно назвать два признака:
·внутренняя однородность;
·внешняя изолированность.
В таблице 1.1 приведено сравнение некоторых параметров задач классификации и кластеризации.
Таблица 1.1
Сравнение классификации и кластеризации
|
Характеристика |
Классификация |
Кластеризация |
| Контролируемость обучения |
Контролируемое обучение |
Неконтролируемое обучение |
| Стратегия |
Обучение с учителем |
Обучение без учителя |
| Наличие метки класса |
Обучающее множество сопровождается меткой, указывающей класс, к которому относится наблюдение |
Метки класса обучающего множества неизвестны |
| Основание для классификации |
Новые данные классифицируются на основании обучающего множества |
Дано множество данных с целью установления существования классов или кластеров данных |
На рисунке 1.1 схематически представлены задачи классификации и кластеризации

Рисунок 1.1 – Сравнение задач классификации и кластеризации
Кластеры могут быть непересекающимися, или эксклюзивными, и пересекающимися. Схематическое изображение непересекающихся и пересекающихся кластеров дано на рисунке 1.2

Рисунок 1.2 – Непересекающиеся и пересекающиеся кластеры
1.2 Процесс кластеризации
Процесс кластеризации зависит от выбранного метода и почти всегда является итеративным. Он может стать увлекательным процессом и включать множество экспериментов по выбору разнообразных параметров, например, меры расстояния, типа стандартизации переменных, количества кластеров и т.д. Однако эксперименты не должны быть самоцелью - ведь конечной целью кластеризации является получение содержательных сведений о структуре исследуемых данных. Полученные результаты требуют дальнейшей интерпретации, исследования и изучения свойств и характеристик объектов для возможности точного описания сформированных кластеров.

Рисунок 1.3 – Общая схема кластеризации
Кластеризация данных включает в себя следующие этапы:
а) Выделение характеристик.
Для начала необходимо выбрать свойства, которые характеризуют наши объекты, ими могут быть количественные характеристики (координаты, интервалы…), качественные характеристики (цвет, статус, воинское звание…) и т.д. Затем стоит попробовать уменьшить размерность пространства характеристических векторов, то есть выделить наиболее важные свойства объектов. Уменьшение размерности ускоряет процесс кластеризации и в ряде случаев позволяет визуально оценивать результаты. Выделенные характеристики стоит нормализовать. Далее все объекты представляются в виде характеристических векторов. Мы будем полностью отождествлять объект с его характеристическим вектором.
б) Определение метрики.
Следующим этапом кластеризации является выбор метрики, по которой мы будем определять близость объектов. Метрика выбирается в зависимости от:
·пространства, в котором расположены объекты;
·неявных характеристик кластеров.
Например, если все координаты объекта непрерывны и вещественны, а кластера должны представлять собой нечто вроде гиперсфер, то используется классическая евклидова метрика (на самом деле, чаще всего так и есть):
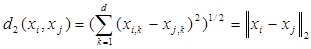 .(1.1) .(1.1)
в) Представление результатов.
Результаты кластеризации должны быть представлены в удобном для обработки виде, чтобы осуществить оценку качества кластеризации. Обычно используется один из следующих способов:
·представление кластеров центроидами;
·представление кластеров набором характерных точек;
·представление кластеров их ограничениями.

Рисунок 1.4 – Способы представления кластеров
Оценка качества кластеризации может быть проведена на основе следующих процедур:
· ручная проверка;
· установление контрольных точек и проверка на полученных кластерах;
· определение стабильности кластеризации путем добавления в модель новых переменных;
· создание и сравнение кластеров с использованием различных методов.
Разные методы кластеризации могут создавать разные кластеры, и это является нормальным явлением. Однако создание схожих кластеров различными методами указывает на правильность кластеризации.
1.3 Алгоритмы кластеризации
Следует отметить, что в результате применения различных методов кластерного анализа могут быть получены кластеры различной формы. Например, возможны кластеры "цепочного" типа, когда кластеры представлены длинными "цепочками", кластеры удлиненной формы и т.д., а некоторые методы могут создавать кластеры произвольной формы. Различные методы могут стремиться создавать кластеры определенных размеров (например, малых или крупных), либо предполагать в наборе данных наличие кластеров различного размера. Некоторые методы кластерного анализа особенно чувствительны к шумам или выбросам, другие - менее. В результате применения различных методов кластеризации могут быть получены неодинаковые результаты, это нормально и является особенностью работы того или иного алгоритма. Данные особенности следует учитывать при выборе метода кластеризации. На сегодняшний день разработано более сотни различных алгоритмов кластеризации.
Классифицировать алгоритмы можно следующим образом:
·строящие «снизу вверх» и «сверху вниз»;
·монотетические и политетические;
·непересекающиеся и нечеткие;
·детерминированные и стохастические;
·потоковые (оnline) и не потоковые;
·зависящие и не зависящие от порядка рассмотрения объектов.
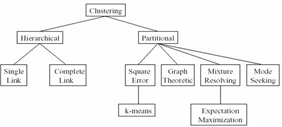
Рисунок 1.5 – Классификация алгоритмов кластеризации
Далее будут рассмотрены основные алгоритмы кластеризации.
1.3.1 Иерархические алгоритмы
Результатом работы иерархических алгоритмов является дендограмма (иерархия), позволяющая разбить исходное множество объектов на любое число кластеров. Два наиболее популярных алгоритма, оба строят разбиение «снизу вверх»:
·single-link – на каждом шаге объединяет два кластера с наименьшим расстоянием между двумя любыми представителями;
·complete-link – на каждом шаге объединяет два кластера с наименьшим расстоянием между двумя наиболее удаленными представителями.
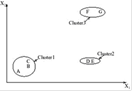
Рисунок 1.6 – Пример single-link алгоритма
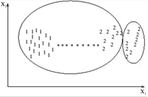
Рисунок 1.7 – Пример complete-link алгоритма
1.3.2 k-Means алгоритм
Данный алгоритм состоит из следующих шагов:
1. Случайно выбрать kточек, являющихся начальными координатами «центрами масс» кластеров (любые k из n объектов, или вообще k случайных точек).
2. Отнести каждый объект к кластеру с ближайшим «центром масс».
3. Пересчитать «центры масс» кластеров согласно текущему членству.
4. Если критерий остановки не удовлетворен, вернуться к шагу 2.
В качестве критерия остановки обычно выбирают один из двух: отсутствие перехода объектов из кластера в кластер на шаге 2 или минимальное изменение среднеквадратической ошибки.
Алгоритм чувствителен к начальному выбору «центр масс».
Рисунок 1.8 – Пример k-Means алгоритма
1.3.3 Минимальное покрывающее дерево
Данный метод производит иерархическую кластеризацию «сверху вниз». Сначала все объекты помещаются в один кластер, затем на каждом шаге один из кластеров разбивается на два, так чтобы расстояние между ними было максимальным.

Рисунок 1.9 – Пример алгоритма минимального покрывающего дерева
1.3.4 Метод ближайшего соседа
Этот метод является одним из старейших методов кластеризации. Он был создан в 1978 году. Он прост и наименее оптимален из всех представленных.
Для каждого объекта вне кластера делаем следующее:
1. Находим его ближайшего соседа, кластер которого определен.
2. Если расстояние до этого соседа меньше порога, то относим его в тот же кластер. Иначе из рассматриваемого объекта создается еще один кластер.
Далее рассматривается результат и при необходимости увеличивается порог, например, если много кластеров из одного объекта.
1.3.5 Алгоритм нечеткой кластеризации
Четкая (непересекающаяся) кластеризация – кластеризация, которая каждый 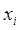 из из 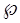 относит только к одному кластеру. относит только к одному кластеру.
Нечеткая кластеризация – кластеризация, при которой для каждого 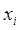 из из 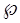 определяется определяется  . .  – вещественное значение, показывающее степень принадлежности – вещественное значение, показывающее степень принадлежности 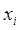 к кластеру j. к кластеру j.
Алгоритм нечеткой кластеризации таков:
1. Выбрать начальное нечеткое разбиение объектов на n кластеров путем выбора матрицы принадлежности 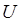 размера размера 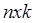 . Обычно . Обычно 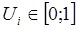 . .
2. Используя матрицу U, найти значение критерия нечеткой ошибки. Например,
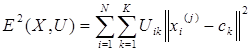 , (1.2) , (1.2)
где 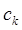 - «центр масс» нечеткого кластера k, - «центр масс» нечеткого кластера k,
 . (1.3) . (1.3)
3. Перегруппировать объекты с целью уменьшения этого значения критерия нечеткой ошибки.
4. Возвращаться в пункт 2 до тех пор, пока изменения матрицы 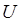 не станут значительными. не станут значительными.
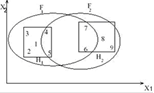
Рисунок 1.10 – Пример алгоритма нечеткой кластеризации
1.3.6 Применение нейронных сетей
Порой для решения задач кластеризации целесообразно использовать нейронные сети. У данного подхода есть ряд особенностей:
·искусственные нейронные сети легко работают в распределенных системах с большой параллелизацией в силу своей природы;
·поскольку искусственные нейронные сети подстраивают свои весовые коэффициенты, основываясь на исходных данных, это помогает сделать выбор значимых характеристик менее субъективным.
Существует масса ИНС, например, персептрон, радиально-базисные сети, LVQ-сети, самоорганизующиеся карты Кохонена, которые можно использовать для решения задачи кластеризации. Но наиболее лучше себя зарекомендовала сеть с применением самоорганизующихся карт Кохонена, которая и выбрана для рассмотрения в данном дипломном проекте.
1.3.7 Генетические алгоритмы
Это алгоритм, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений. Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе.
Задача формализуется таким образом, чтобы её решение могло быть закодировано в виде вектора («генотипа») генов. Где каждый ген может быть битом, числом или неким другим объектом. В классических реализациях ГА предполагается, что генотип имеет фиксированную длину. Однако существуют вариации ГА, свободные от этого ограничения.
Общая схема данного подхода:
1. Выбрать начальную случайную популяцию множества решений и получить оценку качества для каждого решения (обычно она пропорциональна 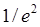 ). ).
2. Создать и оценить следующую популяцию решений, используя эволюционные операторы: оператор выбора – с большой вероятностью предпочитает хорошие решения; оператор рекомбинации (обычно это «кроссовер») – создает новое решение на основе рекомбинации из существующих; оператор мутации – создает новое решение на основе случайного незначительного изменения одного из существующих решений.
3. Повторять шаг 2 до получения нужного результата.
Главным достоинством генетических алгоритмов в данном применении является то, что они ищут глобальное оптимальное решение. Большинство популярных алгоритмов оптимизации выбирают начальное решение, которое затем изменяется в ту или иную сторону. Таким образом получается хорошее разбиение, но не всегда самое оптимальное. Операторы рекомбинации и мутации позволяют получить решения, сильно не похожее на исходное – таким образом осуществляется глобальный поиск.

Рисунок 1.11 – Пример генетического алгоритма
1.4 Применение кластеризации
Кластерный анализ применяется в различных областях. Он полезен, когда нужно классифицировать большое количество информации, например, обзор многих опубликованных исследований, проводимых с помощью кластерного анализа.
Наибольшее применение кластеризация первоначально получила в таких науках как биология, антропология, психология. Для решения экономических задач кластеризация длительное время мало использовалась из-за специфики экономических данных и явлений. Так, в медицине используется кластеризация заболеваний, лечения заболеваний или их симптомов, а также таксономия пациентов, препаратов и т.д. В археологии устанавливаются таксономии каменных сооружений и древних объектов и т.д. В менеджменте примером задачи кластеризации будет разбиение персонала на различные группы, классификация потребителей и поставщиков, выявление схожих производственных ситуаций, при которых возникает брак. В социологии задача кластеризации - разбиение респондентов на однородные группы. В маркетинговых исследованиях кластерный анализ применяется достаточно широко - как в теоретических исследованиях, так и практикующими маркетологами, решающими проблемы группировки различных объектов. При этом решаются вопросы о группах клиентов, продуктов и т.д.
Так, одной из наиболее важных задач при применении кластерного анализа в маркетинговых исследованиях является анализ поведения потребителя, а именно: группировка потребителей в однородные классы для получения максимально полного представления о поведении клиента из каждой группы и о факторах, влияющих на его поведение. Важной задачей, которую может решить кластерный анализ, является позиционирование, т.е. определение ниши, в которой следует позиционировать новый продукт, предлагаемый на рынке. В результате применения кластерного анализа строится карта, по которой можно определить уровень конкуренции в различных сегментах рынка и соответствующие характеристики товара для возможности попадания в этот сегмент. С помощью анализа такой карты возможно определение новых, незанятых ниш на рынке, в которых можно предлагать существующие товары или разрабатывать новые.
Кластерный анализ также может быть удобен, например, для анализа клиентов компании. Для этого все клиенты группируются в кластеры, и для каждого кластера вырабатывается индивидуальная политика. Такой подход позволяет существенно сократить объекты анализа, и, в то же время, индивидуально подойти к каждой группе клиентов.
Таким образом, кластеризация, во-первых, применятся для анализа данных (упрощение работы с информацией, визуализация данных). Использование кластеризации упрощает работу с информацией, так как:
·достаточно работать с k представителями кластеров;
·легко найти «похожие» объекты – такой поиск применяется в ряде поисковых движков;
·происходит автоматическое построение каталогов;
·наглядное представление кластеров позволяет понять структуру множества объектов в пространстве.
Во-вторых, для группировки и распознавания объектов. Для распознавания образов характерно:
·построение кластеров на основе большого набора учебных данных;
·присвоение каждому из кластеров соответствующей метки;
·ассоциирование каждого объекта, полученного на вход алгоритма распознавания, с меткой соответствующего кластера.
Для группировки объектов характерно:
·сегментация изображений
·уменьшение количества информации

Рисунок 1.12 – Пример сегментации изображения
В-третьих, для извлечения и поиска информации, построения удобных классификаторов.
Извлечение и поиск информации можно рассмотреть на примере книг в библиотеке. Это наиболее известная система не автоматической классификации – LCC (LibraryofCongressClassification):
·метка Q означает книги по науке;
·подкласс QA – книги по математике;
·метки с QA76 до QA76.8 – книги по теоретической информатике.
Проблемами такой классификация является то, что иногда классификация отстает от быстрого развития некоторых областей науки, а также возможность отнести каждую книгу только к одной категории. Однако в этом случае приходит на помощь автоматическая кластеризация с нечетким разбиением на группы, что решает проблему одной категории, также новые кластера вырастают одновременно с развитием той или иной области науки.
2. СЕТЬ КОХОНЕНА
Сеть Кохонена - это одна из разновидностей нейронных сетей, которые используют неконтролируемое обучение. При таком обучении обучающее множество состоит лишь из значений входных переменных, в процессе обучения нет сравнивания выходов нейронов с эталонными значениями. Можно сказать, что такая сеть учится понимать структуру данных.
Идея сети Кохонена принадлежит финскому ученому Тойво Кохонену (1982 год). Основной принцип работы сетей - введение в правило обучения нейрона информации относительно его расположения.
В основе идеи сети Кохонена лежит аналогия со свойствами человеческого мозга. Кора головного мозга человека представляет собой плоский лист и свернута складками. Таким образом, можно сказать, что она обладает определенными топологическими свойствами (участки, ответственные за близкие части тела, примыкают друг к другу и все изображение человеческого тела отображается на эту двумерную поверхность). Во многих моделях ИНС решающую роль играют связи между нейронами, определяемые весовыми коэффициентами и указывающие место нейрона в сети. Однако в биологических системах, на пример, таких как мозг, соседние нейроны, получая аналогичные входные сигналы, реагируют на них сходным образом, т. е. группируются, образуя некоторые области. Поскольку при обработке многомерного входного образа осуществляется его проецирование на область меньшей размерности с сохранением его топологии, часто подобные сети называют картами (self-organizing feature map). В таких сетях существенным является учет взаимного расположения нейронов одного слоя.
Сеть Кохонена (самоорганизующаяся карта) относится к самоорганизующимся сетям, которые при поступлении входных сигналов, в отличие от сетей, использующих обучение с учителем, не получают информацию о желаемом выходном сигнале. В связи с этим невозможно сформировать критерий настройки, основанный на рассогласовании реальных и требуемых выходных сигналов ИНС, поэтому весовые параметры сети корректируют, исходя из других соображений. Все предъявляемые входные сигналы из заданного обучающего множества самоорганизующаяся сеть в процессе обучения разделяет на классы, строя так называемые топологические карты.
2.1 Структура сети Кохонена
Сеть Кохонена использует следующую модель (рисунок 2.1): сеть состоит из М нейронов, образующих прямоугольную решетку на плоскости — слой.

Рисунок 2.1 – Модель сети Кохонена
К нейронам, расположенным в одном слое, представляющем собой двумерную плоскость, подходят нервные волокна, по которым поступает N-мерный входной сигнал. Каждый нейрон характеризуется своим положением в слое и весовым коэффициентом. Положение нейронов, в свою очередь, характеризуется некоторой метрикой и определяется топологией слоя, при которой соседние нейроны во время обучения влияют друг на друга сильнее, чем расположенные дальше. Каждый нейрон образует взвешенную сумму входных сигналов с 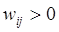 , если синапсы ускоряющие, и , если синапсы ускоряющие, и  - если тормозящие. Наличие связей между нейронами приводит к тому, что при возбуждении одного из них можно вычислить возбуждение остальных нейронов в слое, причем это возбуждение с увеличением расстояния от возбужденного нейрона уменьшается. Поэтому центр возникающей реакции слоя на полученное раздражение соответствует местоположению возбужденного нейрона. Изменение входного обучающего сигнала приводит к максимальному возбуждению другого нейрона и соответственно — к другой реакции слоя. Сеть Кохонена может рассматриваться как дальнейшее развитие LVQ (LearningVectorQuantization). Отличие их состоит в способах обучения. - если тормозящие. Наличие связей между нейронами приводит к тому, что при возбуждении одного из них можно вычислить возбуждение остальных нейронов в слое, причем это возбуждение с увеличением расстояния от возбужденного нейрона уменьшается. Поэтому центр возникающей реакции слоя на полученное раздражение соответствует местоположению возбужденного нейрона. Изменение входного обучающего сигнала приводит к максимальному возбуждению другого нейрона и соответственно — к другой реакции слоя. Сеть Кохонена может рассматриваться как дальнейшее развитие LVQ (LearningVectorQuantization). Отличие их состоит в способах обучения.
2.2 Обучение сети Кохонена
Сеть Кохонена, в отличие от многослойной нейронной сети, очень проста; она представляет собой два слоя: входной и выходной. Элементы карты располагаются в некотором пространстве, как правило, двумерном.
Сеть Кохонена обучается методом последовательных приближений. В процессе обучения таких сетей на входы подаются данные, но сеть при этом подстраивается не под эталонное значение выхода, а под закономерности во входных данных. Начинается обучение с выбранного случайным образом выходного расположения центров.
В процессе последовательной подачи на вход сети обучающих примеров определяется наиболее схожий нейрон (тот, у которого скалярное произведение весов и поданного на вход вектора минимально). Этот нейрон объявляется победителем и является центром при подстройке весов у соседних нейронов. Такое правило обучения предполагает "соревновательное" обучение с учетом расстояния нейронов от "нейрона-победителя".
Обучение при этом заключается не в минимизации ошибки, а в подстройке весов (внутренних параметров нейронной сети) для наибольшего совпадения с входными данными.
Основной итерационный алгоритм Кохонена последовательно проходит ряд эпох, на каждой из которых обрабатывается один пример из обучающей выборки. Входные сигналы последовательно предъявляются сети, при этом желаемые выходные сигналы не определяются. После предъявления достаточного числа входных векторов синаптические веса сети становятся способны определить кластеры. Веса организуются так, что топологически близкие узлы чувствительны к похожим входным сигналам.
В результате работы алгоритма центр кластера устанавливается в определенной позиции, удовлетворительным образом кластеризующей примеры, для которых данный нейрон является "победителем". В результате обучения сети необходимо определить меру соседства нейронов, т.е. окрестность нейрона-победителя, которая представляет собой несколько нейронов, которые окружают нейрон-победитель.
Сначала к окрестности принадлежит большое число нейронов, далее ее размер постепенно уменьшается. Сеть формирует топологическую структуру, в которой похожие примеры образуют группы примеров, близко находящиеся на топологической карте.
Рассмотрим это более подробнее. Кохонен существенно упростил решение задачи, выделяя из всех нейронов слоя лишь один с-й нейрон, для которого взвешенная сумма входных сигналов максимальна:
 . (2.1) . (2.1)
Отметим, что весьма полезной операцией предварительной об работки входных векторов является их нормализация:
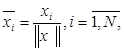 (2.2) (2.2)
превращающая векторы входных сигналов в единичные с тем же направлением.
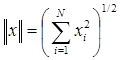 (2.3) (2.3)
В этом случае вследствие того, что сумма весов каждого нейрона одного слоя  для всех нейронов этого слоя одинакова и для всех нейронов этого слоя одинакова и 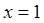 , условие (2.1) эквивалентно условию: , условие (2.1) эквивалентно условию:
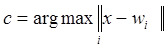 .(2.4) .(2.4)
Таким образом, будет активирован только тот нейрон, вектор весов которого w наиболее близок к входному вектору х. А так как перед началом обучения неизвестно, какой именно нейрон будет активироваться при предъявлении сети конкретного входного вектора, сеть обучается без учителя, т. е. самообучается. Вводя потенциальную функцию — функцию расстояния 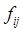 («соседства») между i-м и j-м нейронами с местоположениями («соседства») между i-м и j-м нейронами с местоположениями 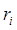 и и  соответственно, монотонно убывающую с увеличением расстояния между этими нейронами, Кохонен предложил следующий алгоритм коррекции весов: соответственно, монотонно убывающую с увеличением расстояния между этими нейронами, Кохонен предложил следующий алгоритм коррекции весов:
 ,(2.5) ,(2.5)
где  - изменяющийся во времени коэффициент усиления (обычно выбирают - изменяющийся во времени коэффициент усиления (обычно выбирают 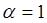 на первой итерации, постепенно уменьшая в процессе обучения до нуля); на первой итерации, постепенно уменьшая в процессе обучения до нуля); 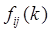 - монотонно убывающая функция. - монотонно убывающая функция.
 , (2.6) , (2.6)
Где 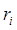 и и  - векторы, определяющие положение нейронов i и j в решетке. При принятой метрике - векторы, определяющие положение нейронов i и j в решетке. При принятой метрике 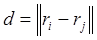 функция функция 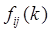 с ростом времени с ростом времени  стремится к нулю. На практике вместо параметра времени стремится к нулю. На практике вместо параметра времени  используют параметр расстояния используют параметр расстояния  , задающий величину области «соседства» и уменьшающийся с течением времени до нуля. Выбор функции , задающий величину области «соседства» и уменьшающийся с течением времени до нуля. Выбор функции 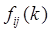 также влияет на величины весов всех нейронов в слое. Очевидно, что для нейрона-победителя также влияет на величины весов всех нейронов в слое. Очевидно, что для нейрона-победителя  : :
 .(2.7) .(2.7)
На рисунке 2.2 показан пример изменения двумерных весов карты 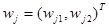 , образующей цепь. При появлении входного образа , образующей цепь. При появлении входного образа  наиболее сильно изменяется весовой вектор нейрона-победителя 5, менее сильно — веса расположенных рядом с ним нейронов 3, 4, 6, 7. А так как нейроны 1, 2, 8, 9 лежат вне области «соседства», их весовые коэффициенты не изменяются. наиболее сильно изменяется весовой вектор нейрона-победителя 5, менее сильно — веса расположенных рядом с ним нейронов 3, 4, 6, 7. А так как нейроны 1, 2, 8, 9 лежат вне области «соседства», их весовые коэффициенты не изменяются.

Рисунок– 2.2 Изменение весов карты Кохонена
Таким образом, алгоритм обучения сети Кохонена может быть описан так:
1. Инициализация
Весовым коэффициентам всех нейронов присваиваются малые случайные значения и осуществляется их нормализация. Выбирается соответствующая потенциальная функция 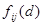 и назначается начальное значение коэффициента усиления и назначается начальное значение коэффициента усиления 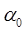 . .
2. Выбор обучающего сигнала
Из всего множества векторов обучающих входных сигналов в соответствии с функцией распределения  выбирается один вектор выбирается один вектор  , который представляет «сенсорный сигнал», предъявляемый сети. , который представляет «сенсорный сигнал», предъявляемый сети.
3. Анализ отклика (выбор нейрона)
По формуле (2.1) определяется активированный нейрон.
4. Процесс обучения
В соответствии с алгоритмом (2.5) изменяются весовые коэффициенты активированного и соседних с ним нейронов до тех пор, пока не будет получено требуемое значение критерия качества обучения или не будет предъявлено заданное число обучающих входных векторов. Окончательное значение весовых коэффициентов совпадает с нормализованными векторами входов.
Поскольку сеть Кохонена осуществляет проецирование N-мерного пространства образов на М-мерную сеть, анализ сходимости алгоритма обучения представляет собой довольно сложную задачу.
Если бы с каждым нейроном слоя ассоциировался один входной вектор, то вес любого нейрона слоя Кохонена мог бы быть обучен с помощью одного вычисления, так как вес нейрона-победителя корректировался бы с 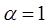 (в соответствии с (2.5) для одномерного случая вес сразу бы попадал в центр отрезка [а, b]). Однако обычно обучающее множество включает множество сходных между собой входных векторов, и сеть Кохонена должна быть обучена активировать один и тот же нейрон для каждого из них. Это достигается усреднением входных векторов путем уменьшения величины, а не при предъявлении каждого последующего входного сигнала. Таким образом, веса, ассоциированные с нейроном, усреднятся и примут значение вблизи «центра» входных сигналов, для которых данный нейрон является «победителем». (в соответствии с (2.5) для одномерного случая вес сразу бы попадал в центр отрезка [а, b]). Однако обычно обучающее множество включает множество сходных между собой входных векторов, и сеть Кохонена должна быть обучена активировать один и тот же нейрон для каждого из них. Это достигается усреднением входных векторов путем уменьшения величины, а не при предъявлении каждого последующего входного сигнала. Таким образом, веса, ассоциированные с нейроном, усреднятся и примут значение вблизи «центра» входных сигналов, для которых данный нейрон является «победителем».
2.3 Выбор функции «соседства»
На рисунке 2.3 показан слой нейронов с нейроном-победителем, отмеченным черным кружком. Поскольку веса всех затемненных нейронов изменяются по-разному, в зависимости от их удаленности от нейрона-победителя, наиболее простым является выбор в качестве  некоторой величины, равной единице при некоторой величины, равной единице при 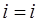 , меньшей единицы для затемненных нейронов, т. е. нейронов, лежащих в непосредственной близости от активированного нейрона, и нулю для остальных, отмеченных светлыми кружками. , меньшей единицы для затемненных нейронов, т. е. нейронов, лежащих в непосредственной близости от активированного нейрона, и нулю для остальных, отмеченных светлыми кружками.

Рисунок 2.3 – Слой нейронов Кохонена
На практике же в качестве  выбирают функции, использующие евклидову метрику: выбирают функции, использующие евклидову метрику:
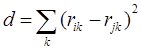 , (2.8) , (2.8)
где 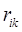 , , 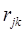 — координаты i-гo и j-го нейронов. — координаты i-гo и j-го нейронов.
К числу наиболее широко используемых потенциальных функций относятся:
а) колоколообразная функция Гаусса
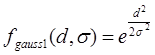 , (2.9) , (2.9)
где 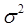 - дисперсия отклонения; - дисперсия отклонения;

Рисунок 2.4 – Колоколообразная функция Гаусса
б) функция «мексиканская шляпа»
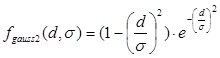 , (2.10) , (2.10)
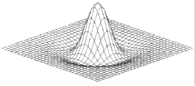
Рисунок 2.5 – Функция «мексиканская шляпа»
в) косинусоидная функция
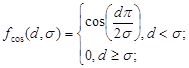 (2.11) (2.11)

Рисунок 2.6 – Косинусоидная функция
г) конусообразная функция
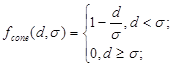 (2.12) (2.12)

Рисунок 2.7 – Конусообразная функция
д) цилиндрическая функция
 (2.13) (2.13)

Рисунок 2.8 – Цилиндрическая функция
2.4 Карта Кохонена
Как правило, сначала строят довольно грубую карту (модель разбиения), постепенно уточняя ее в процессе обучения. Для этого необходимо медленно изменять не только параметр 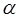 , но и, например, параметр , но и, например, параметр 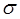 в формуле (2.9). Одним из эффективных способов изменения этих параметров является следующий: в формуле (2.9). Одним из эффективных способов изменения этих параметров является следующий:
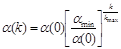 , (2.14) , (2.14)
 , (2.15) , (2.15)
где 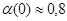 ; ; 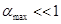 ; ; 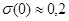 ; ;  - параметры, определяющие крутизну функции - параметры, определяющие крутизну функции  ; ; 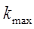 - задаваемое число итераций. - задаваемое число итераций.
На рисунке 2.9 показан процесс построения карты Кохонена, представляющей собой двумерную решетку, образованную путем соединения соседних нейронов, находящихся в узлах решетки. Исходя из начальных условий и используя алгоритм обучения (2.5), сеть по мере увеличения числа обучающих входных образов развивается и приобретает вид решетки. Внизу каждого рисунка поставлено количество образов, на основании которых получена соответствующая сеть.

Рисунок 2.9 – Построение карты Кохонена
Уникальность метода самоорганизующихся карт состоит в преобразовании n-мерного пространства в двухмерное. Применение двухмерных сеток связано с тем, что существует проблема отображения пространственных структур большей размерности. Имея такое представление данных, можно визуально определить наличие или отсутствие взаимосвязи во входных данных.
Нейроны карты Кохонена располагают в виде двухмерной матрицы, раскрашивают эту матрицу в зависимости от анализируемых параметров нейронов.
На рисунке 2.10 приведен пример карты Кохонена.

Рисунок 2.10 – Пример карты Кохонена
На рисунке 2.11 приведена раскраска карты, а точнее, ее i-го признака, в трехмерном представлении. Как мы видим, темно-синие участки на карте соответствуют наименьшим значениям показателя, красные - самым высоким.

Рисунок 2.11 – Раскраска i-го признака в трехмерном пространстве
Теперь, возвращаясь к рисунку 2.10, мы можем сказать, какие объекты имеют наибольшие значения рассматриваемого показателя (группа объектов, обозначенная красным цветом), а какие - наименьшие значения (группа объектов, обозначенная синим цветом).
Таким образом, карты Кохонена можно отображать:
·в двухмерном виде, тогда карта раскрашивается в соответствии с уровнем выхода нейрона;
·в трехмерном виде.
В результате работы алгоритма получаем такие карты:
а) Карта входов нейронов.
Веса нейронов подстраиваются под значения входных переменных и отображают их внутреннюю структуру. Для каждого входа рисуется своя карта, раскрашенная в соответствии со значением конкретного веса нейрона. При анализе данных используют несколько карт входов. На одной из карт выделяют область определенного цвета - это означает, что соответствующие входные примеры имеют приблизительно одинаковое значение соответствующего входа. Цветовое распределение нейронов из этой области анализируется на других картах для определения схожих или отличительных характеристик.
б) Карта выходов нейронов.
На карту выходов нейронов проецируется взаимное расположение исследуемых входных данных. Нейроны с одинаковыми значениями выходов образуют кластеры - замкнутые области на карте, которые включают нейроны с одинаковыми значениями выходов.
в) Специальные карты.
Это карта кластеров, матрица расстояний, матрица плотности попадания и другие карты, которые характеризуют кластеры, полученные в результате обучения сети Кохонена.
Координаты каждой карты определяют положение одного нейрона. Так, координаты [15:30] определяют нейрон, который находится на пересечении 15-го столбца с 30-м рядом в матрице нейронов. Важно понимать, что между всеми рассмотренными картами существует взаимосвязь - все они являются разными раскрасками одних и тех же нейронов. Каждый пример из обучающей выборки имеет одно и то же расположение на всех картах.
Полученную карту можно использовать как средство визуализации при анализе данных. В результате обучения карта Кохонена классифицирует входные примеры на кластеры (группы схожих примеров) и визуально отображает многомерные входные данные на плоскости нейронов.
При реализации сети Кохонена возникают следующие проблемы:
1. Выбор коэффициента обучения 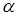
Этот выбор влияет как на скорость обучения, так и на устойчивость получаемого решения. Очевидно, что процесс обучения ускоряется (скорость сходимости алгоритма обучения увеличивается) при выборе 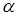 близким к единице. Однако в этом случае предъявление сети различных входных векторов, относящихся к одному классу, приведет к изменениям соответствующего вектора весовых коэффициентов. Напротив, при близким к единице. Однако в этом случае предъявление сети различных входных векторов, относящихся к одному классу, приведет к изменениям соответствующего вектора весовых коэффициентов. Напротив, при  0 скорость обучения будет медленной, однако вектор весовых коэффициентов, достигнув центра класса, при подаче на вход сети различных сигналов, относящихся к одному классу, будет оставаться вблизи этого центра. Поэтому одним из путей ускорения процесса обучения при одновременном обеспечении получения устойчивого решения является выбор переменного 0 скорость обучения будет медленной, однако вектор весовых коэффициентов, достигнув центра класса, при подаче на вход сети различных сигналов, относящихся к одному классу, будет оставаться вблизи этого центра. Поэтому одним из путей ускорения процесса обучения при одновременном обеспечении получения устойчивого решения является выбор переменного 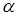 с с  1 на начальных этапах обучения и 1 на начальных этапах обучения и  0 - на заключительных. К сожалению, такой подход не применим в тех случаях, когда сеть должна непрерывно подстраиваться к предъявляемым ей новым входным сигналам. 0 - на заключительных. К сожалению, такой подход не применим в тех случаях, когда сеть должна непрерывно подстраиваться к предъявляемым ей новым входным сигналам.
2. Рандомизация весов
Рандомизация весов слоя Кохонена может породить серьезные проблемы при обучении, так как в результате этой операции весовые векторы распределяются равномерно по поверхности гиперсферы. Как правило, входные векторы распределены неравномерно и группируются на относительно малой части поверхности гиперсферы. Поэтому большинство весовых векторов окажутся настолько удаленными от любого входного вектора, что не будут активированы и станут бесполезными. Более того, оставшихся активированных нейронов может оказаться слишком мало, чтобы разбить близко расположенные входные векторы на кластеры.
3. Выбор начальных значений векторов весовых коэффициентов и нейронов.
Если начальные значения выбраны неудачно, т. е. расположенными далеко от предъявляемых входных векторов, то нейрон не окажется победителем ни при каких входных сигналах, а, следовательно, не обучится.
На рисунке 2.12 показан случай, когда начальное расположение весов 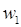 и и  привело к тому, что после обучения сети все предъявляемые образы классифицируют нейроны с весами привело к тому, что после обучения сети все предъявляемые образы классифицируют нейроны с весами  , ,  , и , и  . Веса же . Веса же 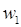 и и  не изменились и могут быть удалены из сети. не изменились и могут быть удалены из сети.

а б
Рисунок 2.12 – Начальное (а) и конечное (б) положения векторов весов
4. Выбор параметра расстояния 
Если сначала параметр  выбран малым или очень быстро уменьшается, то далеко расположенные друг от друга нейроны не могут влиять друг на друга. Хотя две части в такой карте настраиваются правильно, общая карта будет иметь топологический дефект (рисунок 2.13). выбран малым или очень быстро уменьшается, то далеко расположенные друг от друга нейроны не могут влиять друг на друга. Хотя две части в такой карте настраиваются правильно, общая карта будет иметь топологический дефект (рисунок 2.13).
5. Количество нейронов в слое
Число нейронов в слое Кохонена должно соответствовать числу классов входных сигналов. Это может быть недопустимо в тех задачах, когда число классов заранее известно.

Рисунок 2.13 – Топологический дефект карты
6. Классы входных сигналов
Слой Кохонена может формировать только классы, представляющие собой выпуклые области входного пространства.
2.5 Задачи, решаемые при помощи карт Кохонена
Самоорганизующиеся карты могут использоваться для решения задач моделирования, прогнозирования, кластеризации, поиска закономерностей в больших массивах данных, выявления наборов независимых признаков и сжатии информации.
Наиболее распространенное применение сетей Кохонена - решение задачи классификации без учителя, т.е. кластеризации.
Напомним, что при такой постановке задачи нам дан набор объектов, каждому из которых сопоставлена строка таблицы (вектор значений признаков). Требуется разбить исходное множество на классы, т.е. для каждого объекта найти класс, к которому он принадлежит.
В результате получения новой информации о классах возможна коррекция существующих правил классификации объектов.
Самым распространенным применением карт Кохонена является:
·разведочный анализ данных
·обнаружение новых явлений
В первом случае сеть Кохонена способна распознавать кластеры в данных, а также устанавливать близость классов. Таким образом, пользователь может улучшить свое понимание структуры данных, чтобы затем уточнить нейросетевую модель. Если в данных распознаны классы, то их можно обозначить, после чего сеть сможет решать задачи классификации. Сети Кохонена можно использовать и в тех задачах классификации, где классы уже заданы, - тогда преимущество будет в том, что сеть сможет выявить сходство между различными классами.
Во втором случае сеть Кохонена распознает кластеры в обучающих данных и относит все данные к тем или иным кластерам. Если после этого сеть встретится с набором данных, непохожим ни на один из известных образцов, то она не сможет классифицировать такой набор и тем самым выявит его новизну.
кластеризация нейронный сеть кохонен
3. МОДЕЛИРОВАНИЕ СЕТИ КЛАСТЕРИЗАЦИИ ДАННЫХ В MATLABNEURALNETWORKTOOLBOX
Программное обеспечение, позволяющее работать с картами Кохонена, сейчас представлено множеством инструментов. Это могут быть как инструменты, включающие только реализацию метода самоорганизующихся карт, так и нейропакеты с целым набором структур нейронных сетей, среди которых - и карты Кохонена; также данный метод реализован в некоторых универсальных инструментах анализа данных.
К инструментарию, включающему реализацию метода карт Кохонена, относятся MATLAB Neural Network Toolbox, SoMine, Statistica, NeuroShell, NeuroScalp, Deductor и множество других.
3.1 Самоорганизующиеся нейронные сети в MATLABNNT
Для создания самоорганизующихся нейронных сетей, являющихся слоем или картой Кохонена, предназначены М-функции newc и newsom cooтветственно.
По команде help selforg можно получить следующую информацию об М-функциях, входящих в состав ППП Neural Network Toolbox и относящихся к построению сетей Кохонена (таблица 3.1):
Таблица 3.1
М-функции, входящие в состав ППП NeuralNetworkToolbox
| Self-organizing networks |
Самоорганизующиеся сети |
| New networks |
Формирование сети |
newc
newsom
|
Создание слоя Кохонена
Создание карты Кохонена
|
| Using networks |
Работа с сетью |
sim
init
adapt
train
|
Моделирование
Инициализация
Адаптация
Обучение
|
| Weight functions |
Функции расстояния и взвешивания |
| negdist |
Отрицательное евклидово расстояние |
| Net input functons |
Функции накопления |
| netsum |
Сумма взвешенных входов |
| Transfer functions |
Функции активации |
| compet |
Конкурирующая функция активации |
Topology
functions
|
Функции описания топологии сети |
gridtop
hextop
randtop
|
Прямоугольная сетка
Гексагональная сетка
Сетка со случайно распределенными узлами
|
| Distance functions |
Функции расстояния |
dist
boxdist
mandist
linkdist
|
Евклидово расстояние
Расстояние максимального координатного смещения
Расстояние суммарного координатного смешения Расстояние связи
|
| Initialization functions |
Функции инициализации сети |
initlay
initwb
initcon
midpoint
|
Послойная инициализация
Инициализация весов и смещений
Инициализация смещений с учетом чувствительности нейронов
Инициализация весов по правилу средней точки
|
| Learning functions |
функции настройки параметров |
learnk
learncon
learnsom
|
Правило настройки весов для слоя Кохонена Правило настройки смещений для слоя Кохонена Правило настройки весов карты Кохонена |
| Adapt functions |
Функции адаптации |
| adaptwb |
Адаптация весов и смещений |
| Training functions |
Функции обучения |
| trainwb1 |
Повекторное обучение весов и смещений |
| Demonstrations |
Демонстрационные примеры |
democ1
demosm1
demosm2
|
Настройка слоя Кохонена
Одномерная карта Кохонена
Двумерная карта Кохонена
|
3.1.1 Архитектура сети
Промоделированная архитектура слоя Кохонена в MATLABNNT показана на рисунке 3.1.

Рисунок 3.1 – Архитектура слоя Кохонена
Нетрудно убедиться, что это слой конкурирующего типа, поскольку в нем применена конкурирующая функция активации. Кроме того, архитектура этого слоя очень напоминает архитектуру скрытого слоя радиальной базисной сети. Здесь использован блок ndist для вычисления отрицательного евклидова расстояния между вектором входа 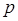 и строками матрицы весов и строками матрицы весов 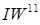 . Вход функции активации . Вход функции активации 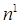 - это результат суммирования вычисленного расстояния с вектором смещения - это результат суммирования вычисленного расстояния с вектором смещения  . Если все смещения нулевые, максимальное значение . Если все смещения нулевые, максимальное значение 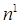 не может превышать 0. Нулевое значение не может превышать 0. Нулевое значение 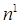 возможно только, когда вектор входа возможно только, когда вектор входа 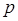 оказывается равным вектору веса одного из нейронов. Если смещения отличны от 0, то возможны и положительные значения для элементов вектора оказывается равным вектору веса одного из нейронов. Если смещения отличны от 0, то возможны и положительные значения для элементов вектора 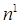 . .
Конкурирующая функция активации анализирует значения элементов вектора 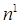 и формирует выходы нейронов, равные 0 для всех нейронов, кроме одного нейрона-победителя, имеющего на входе максимальное значение. Таким образом, вектор выхода слоя и формирует выходы нейронов, равные 0 для всех нейронов, кроме одного нейрона-победителя, имеющего на входе максимальное значение. Таким образом, вектор выхода слоя  имеет единственный элемент, равный 1, который соответствует нейрону-победителю, а остальные равны 0. Такая активационная характеристика может быть описана следующим образом; имеет единственный элемент, равный 1, который соответствует нейрону-победителю, а остальные равны 0. Такая активационная характеристика может быть описана следующим образом;
 (3.1) (3.1)
Заметим, что эта активационная характеристика устанавливается не на отдельный нейрон, а на слой. Поэтому такая активационная характеристика и получила название конкурирующей. Номер активного нейрона 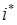 определяет ту группу (кластер), к которой наиболее близок входной вектор. определяет ту группу (кластер), к которой наиболее близок входной вектор.
3.1.2 Создание сети
Для формирования слоя Кохонена предназначена М-функция newc. Покажем, как она работает, на простом примере. Предположим, что задан массив из четырех двухэлементных векторов, которые надо разделить на 2 класса:
р = [.1 .8 .1 .9; .2 .9 .1 .8]
р =
0.1000 0.8000 0.1000 0.9000
0.2000 0.9000 0.1000 0.8000.
В этом примере нетрудно видеть, что 2 вектора расположены вблизи точки (0,0) и 2 вектора - вблизи точки (1,1). Сформируем слой Кохонена с двумя нейронами для анализа двухэлементных векторов входа с диапазоном значений от 0 до 1:
net = newc([0 1; 0 1],2).
Первый аргумент указывает диапазон входных значений, второй определяет количество нейронов в слое. Начальные значения элементов матрицы весов задаются как среднее максимального и минимального значений, т. е. в центре интервала входных значений; это реализуется по умолчанию с помощью М-функции midpoint при создании сети. Убедимся, что это действительно так:
wts = net.IW{l,l}
wts =
0.5000 0.5000
0.5000 0.5000.
Определим характеристики слоя Кохонена:
net.layers{1}
ans =
dimensions: 2
distanсeFcn: 'dist'
distances:[2x2 double]
initFcn:' initwb '
netinputFcn:'netsum'
positions:[0 1]
size:2
topologyFcn:'hextop'
transferFcn:'compet'
userdata:[1x1 struct].
Из этого описания следует, что сеть использует функцию евклидова расстояния dist, функцию инициализации initwb, функцию обработки входов netsum, функцию активации compet и функцию описания топологии hextop.
Характеристики смещений следующие:
net.biases{1}
ans =
initFcn:'initcon'
learn:1
learnFcn:'learncon'
learnParam:[1x1 struct]
size:2
userdata:[1x1 struct].
Смещения задаются функцией initcon и для инициализированной сети равны
net.b{l}
ans =
5.4366
5.4366.
Функцией настройки смещений является функция lеаrcon, обеспечивающая настройку с учетом параметра активности нейронов.
Элементы структурной схемы слоя Кохонена показаны на рисунке 3.2, а-б и могут быть получены с помощью оператора:
gensim(net)
Они наглядно поясняют архитектуру и функции, используемые при построении слоя Кохонена.
Теперь, когда сформирована самоорганизующаяся нейронная сеть, требуется обучить сеть решению задачи кластеризации данных. Напомним, что каждый нейрон блока compet конкурирует за право ответить на вектор входа 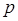 . Если все смещения равны 0, то нейрон с вектором веса, самым близким к вектору входа . Если все смещения равны 0, то нейрон с вектором веса, самым близким к вектору входа 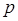 , выигрывает конкуренцию и возвращает на выходе значение 1; все другие нейроны возвращают значение 0. , выигрывает конкуренцию и возвращает на выходе значение 1; все другие нейроны возвращают значение 0.
 
а б
Рисунок 3.2 – Элементы структурной схемы слоя Кохонена
3.1.3 Правило обучения слоя Кохонена
Правило обучения слоя Кохонена, называемое также правилом Кохонена, заключается в том, чтобы настроить нужным образом элементы матрицы весов. Предположим, что нейрон  победил при подаче входа победил при подаче входа  на шаге самообучения на шаге самообучения  , тогда строка , тогда строка  матрицы весов корректируется в соответствии с правилом Кохонена следующим образом: матрицы весов корректируется в соответствии с правилом Кохонена следующим образом:
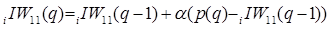 . (3.2) . (3.2)
Правило Кохонена представляет собой рекуррентное соотношение, которое обеспечивает коррекцию строки  матрицы весов добавлением взвешенной разности вектора входа и значения строки на предыдущем шаге. Таким образом, вектор веса, наиболее близкий к вектору входа, модифицируется так, чтобы расстояние между ними стало еще меньше. Результат такого обучения будет заключаться в том, что победивший нейрон, вероятно, выиграет конкуренцию и в том случае, когда будет представлен новый входной вектор, близкий к предыдущему, и его победа менее вероятна, когда будет представлен вектор, существенно отличающийся от предыдущего. Когда на вход сети поступает все большее и большее число векторов, нейрон, являющийся ближайшим, снова корректирует свой весовой вектор. В конечном счете, если в слое имеется достаточное количество нейронов, то каждая группа близких векторов окажется связанной с одним из нейронов слоем. В этом и заключается свойство самоорганизации слоя Кохонена. матрицы весов добавлением взвешенной разности вектора входа и значения строки на предыдущем шаге. Таким образом, вектор веса, наиболее близкий к вектору входа, модифицируется так, чтобы расстояние между ними стало еще меньше. Результат такого обучения будет заключаться в том, что победивший нейрон, вероятно, выиграет конкуренцию и в том случае, когда будет представлен новый входной вектор, близкий к предыдущему, и его победа менее вероятна, когда будет представлен вектор, существенно отличающийся от предыдущего. Когда на вход сети поступает все большее и большее число векторов, нейрон, являющийся ближайшим, снова корректирует свой весовой вектор. В конечном счете, если в слое имеется достаточное количество нейронов, то каждая группа близких векторов окажется связанной с одним из нейронов слоем. В этом и заключается свойство самоорганизации слоя Кохонена.
Настройка параметров сети по правилу Кохонена реализована в виде М-функции learnk.
3.1.4 Правило настройки смещений
Одно из ограничений всякого конкурирующего слоя состоит в том, что некоторые нейроны оказываются незадействованными. Это проявляется в том, что нейроны, имеющие начальные весовые векторы, значительно удаленные от векторов входа, никогда не выигрывают конкуренции, независимо от того как долго продолжается обучение. В результате оказывается, что такие векторы не используются при обучении и соответствующие нейроны никогда не оказываются победителями. Такие нейроны-неудачники называются "мертвыми" нейронами, поскольку они не выполняют никакой полезной функции. Чтобы исключить такую ситуацию и сделать нейроны чувствительными к поступающим на вход векторам, используются смещения, которые позволяют нейрону стать конкурентным с нейронами-победителями. Этому способствует положительное смещение, которое добавляется к отрицательному расстоянию удаленного нейрона.
Соответствующее правило настройки, учитывающее нечувствительность мертвых нейронов, реализовано в виде М-функции learncon и заключается в следующем - в начале процедуры настройки всем нейронам конкурирующего слоя присваивается одинаковый параметр активности:
 , (3.3) , (3.3)
где  - количество нейронов конкурирующего слоя, равное числу кластеров. В процессе настройки М-функция learncon корректирует этот параметр таким образом, чтобы его значения для активных нейронов становились больше, а для неактивных нейронов меньше. Соответствующая формула для вектора приращений параметров активности выглядит следующим образом: - количество нейронов конкурирующего слоя, равное числу кластеров. В процессе настройки М-функция learncon корректирует этот параметр таким образом, чтобы его значения для активных нейронов становились больше, а для неактивных нейронов меньше. Соответствующая формула для вектора приращений параметров активности выглядит следующим образом:
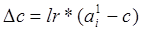 , (3.4) , (3.4)
где  - параметр скорости настройки; - параметр скорости настройки;  -вектор, элемент -вектор, элемент  которого равен 1, а остальные - 0. которого равен 1, а остальные - 0.
Нетрудно убедиться, что для всех нейронов, кроме нейрона-победителя, приращения отрицательны. Поскольку параметры активности связаны со смещениями соотношением (в обозначениях системы MATLAB):
 , (3.5) , (3.5)
то из этого следует, что смещение для нейрона-победителя уменьшится, а смещения для остальных нейронов немного увеличатся.
М-функция learnсon использует следующую формулу для расчета приращений вектора смещений:
 . (3.6) . (3.6)
Параметр скорости настройки  по умолчанию равен 0.001, и его величина обычно на порядок меньше соответствующего значения для М-функции learnk. Увеличение смещений для неактивных нейронов позволяет расширить диапазон покрытия входных значений, и неактивный нейрон начинает формировать кластер. В конечном счете он может начать притягивать новые входные векторы - это дает два преимущества. Первое преимущество, если нейрон не выигрывает конкуренции, потому что его вектор весов существенно отличается от векторов, поступающих на вход сети, то его смещение по мере обучения становится достаточно большим и он становится конкурентоспособным. Когда это происходит, его вектор весов начинает приближаться к некоторой группе векторов входа. Как только нейрон начинает побеждать, его смещение начинает уменьшаться. Таким образом, задача активизации "мертвых" нейронов оказывается решенной. Второе преимущество, связанное с настройкой смещений, состоит в том, что они позволяют выровнять значения параметра активности и обеспечить притяжение приблизительно одинакового количества векторов входа. Таким образом, если один из кластеров притягивает большее число векторов входа, чем другой, то более заполненная область притянет дополнительное количество нейронов и будет поделена на меньшие по размерам кластеры. по умолчанию равен 0.001, и его величина обычно на порядок меньше соответствующего значения для М-функции learnk. Увеличение смещений для неактивных нейронов позволяет расширить диапазон покрытия входных значений, и неактивный нейрон начинает формировать кластер. В конечном счете он может начать притягивать новые входные векторы - это дает два преимущества. Первое преимущество, если нейрон не выигрывает конкуренции, потому что его вектор весов существенно отличается от векторов, поступающих на вход сети, то его смещение по мере обучения становится достаточно большим и он становится конкурентоспособным. Когда это происходит, его вектор весов начинает приближаться к некоторой группе векторов входа. Как только нейрон начинает побеждать, его смещение начинает уменьшаться. Таким образом, задача активизации "мертвых" нейронов оказывается решенной. Второе преимущество, связанное с настройкой смещений, состоит в том, что они позволяют выровнять значения параметра активности и обеспечить притяжение приблизительно одинакового количества векторов входа. Таким образом, если один из кластеров притягивает большее число векторов входа, чем другой, то более заполненная область притянет дополнительное количество нейронов и будет поделена на меньшие по размерам кластеры.
3.1.5 Обучение сети
Реализуем 10 циклов обучения. Для этого можно использовать функции train или adapt:
net.trainParam.epochs = 10
net = train(net,p)
net.adaptParam.passes = 10
[net,y,e] = adapt(net,mat2cell(p)).
Заметим, что для сетей с конкурирующим слоем по умолчанию используется обучающая функция trainwbl, которая на каждом цикле обучения случайно выбирает входной вектор и предъявляет его сети; после этого производится коррекция весов и смещений.
Выполним моделирование сети после обучения:
а = sim(net,p)
ас = vec2ind(a)
ас = 2 1 2 1.
Видим, что сеть обучена классификации векторов входа на 2 кластера: первый расположен в окрестности вектора (0,0), второй - в окрестности вектора (1,1). Результирующие веса и смещения равны:
wtsl = net.IW{l,l}
b1 = net.b{l}
wts1 =
0.58383 0.58307
0.41712 0.42789
b1=
5.4152
5.4581.
Заметим, что первая строка весовой матрицы действительно близка к вектору (1,1), в то время как вторая строка близка к началу координат. Таким образом, сформированная сеть обучена классификации входов. В процессе обучения каждый нейрон в слое, весовой вектор которого близок к группе векторов входа, становится определяющим для этой группы векторов. В конечном счете, если имеется достаточное число нейронов, каждая группа векторов входа будет иметь нейрон, который выводит 1, когда представлен вектор этой группы, и 0 в противном случае, или, иными словами, формируется кластер. Таким образом, слой Кохонена действительно решает задачу кластеризации векторов входа.
3.1.6 Моделирование кластеризации данных
Функционирование слоя Кохонена можно пояснить более наглядно, используя графику системы MATLAB. Рассмотрим 48 случайных векторов на плоскости, формирующих 8 кластеров, группирующихся около своих центров. На графике, приведенном на рисунке 3.3, показано 48 двухэлементных векторов входа.
Сформируем координаты случайных точек и построим план их расположения на плоскости:
с = 8
n = 6 % Число кластеров, векторов в кластере
d = 0.5 % Среднеквадратичное отклонение от центра кластера
х = [-10 10;-5 5] % Диапазон входных значений
[r,q] = size(x); minv = min(x1)1; maxv = mах(х1)1
v = rand(r, e).С{maxv - minv) *ones(l,c) + xninv*ones (l,c) )t = c*n % Число точек
v= [v v v v v]; v=v+randn{r,t)*d % Координаты точек
Р = v
plot(P(l,:), P(2,:),'+k') % (рисунок 3.3)
title('Векторы входа'), xlabel('Р(1,:)'), ylabel('P(2,:)').
Векторы входа, показанные на рисунке 3.3, относятся к различным классам.

Рисунок 3.3 – Двухэлементные векторы входа
Применим конкурирующую сеть из восьми нейронов для того, чтобы распределить их по классам:
net = newc([-2 12;-1 6], 8 ,0.1)
w0 =net.IW{l}
b0 = net.b{l}
c0 = exp(l)./b0.
Начальные значения весов, смещений и параметров активности нейронов представлены ниже:
w0 =b0 =с0 =
0.50.2521.7460.125
0.50.2521,7460.125
0.50.2521.7460.125
0-50.2521.7460.125
0.50.2521.7460.125
0.50.2521.7460.125
0.50.2521.7460.125
0.50.2521.7460.125.
После обучения в течение 500 циклов получим:
net.trainParam.epochs = 500
net = train(net,P)
w = net.IW{l} bn = net.b{l}
cn = exp(1)./bn
wn=bn=cn=
6.2184 2.423922.1370,123
1.3277 0.9470121.7180.125
0.31139 0.4093521.1920.128
3.543 4.584521.4720.127
3.4617 2.8S9621.9570.124
4 3171 1.427821.1850.128
6.7065 0.4369623.0060.118
0.97S17 0.1724221.420.127.
Как следует из приведенных таблиц, центры кластеризации распределились по восьми областям, показанным на рисунке 3.4, а; смещения отклонились в обе стороны от исходного значения 21.746 также, как и параметры активности нейронов, показанные на рисунке 3.4, б.
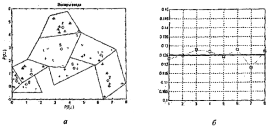
Рисунок 3.4 – Полученные центры кластеризации
Рассмотренная самонастраивающаяся сеть Кохонена является типичным примером сети, которая реализует процедуру обучения без учителя.
3.2 Карта Кохонена в MATLABNNT
Самоорганизующаяся сеть в виде карты Кохонена предназначена для решения задач кластеризации входных векторов. В отличие от слоя Коконена карта Кохонена поддерживает такое топологическое свойство, когда близким кластерам входных векторов соответствуют близко расположенные нейроны.
Первоначальная топология размещения нейронов в слое Кохонена задается М-функциями gridtop, hextop или randtop, что соответствует размещению нейронов в узлах либо прямоугольной, либо гексагональной сетки, либо в узлах сетки со случайной топологией. Расстояния между нейронами вычисляются с помощью специальных функций вычисления расстояний dist, boxdist, linkdist и mandist.
Карта Кохонена для определения нейрона-победителя использует ту же процедуру, какая применяется и в слое Кохонена. Однако на карте Кохонена одновременно изменяются весовые коэффициенты соседних нейронов в соответствии со следующим соотношением:
 . (3.7) . (3.7)
В этом случае окрестность нейрона-победителя включает все нейроны, которые находятся в пределах некоторого радиуса  : :
 . (3.8) . (3.8)
Чтобы пояснить понятие окрестности нейрона, обратимся к рисунку 3.5.

Рисунок 3.5 – Окрестности нейрона
Левая часть рисунка соответствует окрестности радиуса 1 для нейрона-победителя с номером 13; правая часть - окрестности радиуса 2 для того же нейрона. Описания этих окрестностей выглядят следующим образом:
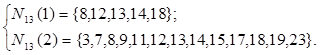
Заметим, что топология карты расположения нейронов не обязательно должна быть двумерной. Это могут быть и одномерные и трехмерные карты, и даже карты больших размерностей. В случае одномерной карты Кохонена, когда нейроны расположены вдоль линии, каждый нейрон будет иметь только двух соседей в пределах радиуса 1 или единственного соседа, если нейрон расположен на конце линии. Расстояния между нейронами можно определять различными способами, используя прямоугольные или гексагональные сетки, однако это никак не влияет на характеристики сети, связанные с классификацией входных векторов.
3.2.1 Топология карты
Как уже отмечалось выше, можно задать различные топологии для карты расположения нейронов, используя М-функции gridtop, hextop, randtop.
Рассмотрим простейшую прямоугольную сетку размера 2x3 для размещения шести нейронов, которая может быть сформирована с помощью функции gridtop:
pos = gridtop(2,3)
pos =
0 10101
0 0 1122
plotsom(pos) % (рисунок 3.6).
Соответствующая сетка показана на рисунке 3.6. Метки position(1, i) и position(2,i) вдоль координатных осей генерируются функцией plotsom и задают позиции расположения нейронов по первой, второй и т. д. размерностям карты.

Рисунок 3.6 – Прямоугольная сетка
Здесь нейрон 1 расположен в точке с координатами (0,0), нейрон 2 - в точке (1,0), нейрон 3 - в точке (0,1) и т. д. Заметим, что, если применить команду gridtop, переставив аргументы местами, получим иное размещение нейронов;
pos=gridtop(3,2)pos =
0 1 2 0 1 2
0 0 0 1 1 1.
Гексагональную сетку можно сформировать с помощью функции hextop:
pos = hextop(2,3)
pos =
0 1.0000 0.5000 1.5000 0 1.0000
0 0 0.8660 0.8660 1.7321 1.7321.
plotsom (pos) % (рисунок 3.7).
Рисунок 3.7 – Гексагональная сетка
Заметим, что М-функция hextop используется по умолчанию при создании карт Кохонена при применении функции newsom.
Сетка со случайным расположением узлов может быть создана с помощью функции randtop:
pos = randtop(2,3)
pos =
0.061787 0.64701 0.40855 0.94383 0 0.65113
0 0.12233 0.90438 0.54745 1.4015 1.5682
plotsom(pos) % (рисунок 3.8).

Рисунок 3.8 – Сетка со случайным расположением узлов
3.2.2 Функции для расчета расстояний
В ППП NNT используется 4 функции для расчета расстояний между узлами сетки.
Функция dist вычисляет евклидово расстояние между нейронами, размещенными в узлах сетки, в соответствии с формулой:
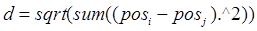 , (3.9) , (3.9)
где  , , 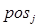 - векторы положения нейронов с номерами i и j. - векторы положения нейронов с номерами i и j.
Обратимся к прямоугольной сетке из шести нейронов (рисунок 3.6) и вычислим соответствующий массив расстояний:
pos = gridtop(2,3)
d = disе(pos)
d =
0 1 1 1.4142 2 2.2361
1 0 1.4142 1 2.2361 2
1 1.4142 0 1 1 1.4142
1.4142 1 1 0 1.4142 1
2 2.2361 1 1.4142 0 1
2.2361 2 1.4142 1 1 0.
Этот массив размера 6х6 описывает расстояния между нейронами и содержит на диагонали нули, поскольку они определяют расстояние нейрона до самого себя, а затем, двигаясь вдоль строки, до второго, третьего и т. д.
На рисунке 3.9 показано расположение нейронов в узлах прямоугольной сетки. Введем понятие окрестности для прямоугольной сетки. В этом случае окрестность размера 1, или просто окрестность 1, включает базовый нейрон и его непосредственных соседей; окрестность 2 включает нейроны из окрестности 1 и их соседей.

Рисунок 3.9 – Расположение нейронов в узлах прямоугольной сетки
Размер, а соответственно и номер окрестности, определяется максимальным значением координаты смещения нейрона от базового. Вводимое таким способом расстояние между нейронами называется расстоянием максимального координатного смещения и может быть вычислено по формуле:
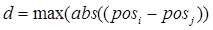 , (3.10) , (3.10)
где  , , 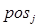 - векторы положения нейронов с номерами i и j. - векторы положения нейронов с номерами i и j.
Для вычисления этого расстояния в ППП NNT предназначена М-функция boxdist. Для конфигурации нейронов, показанной на рисунке 3.6, эти расстояния равны:
роs = gridtop(2,3)
d = boxdist(pos)
d=
0 1 1 1 2 2
1 0 1 1 2 2
1 1 0 1 1 1
1 1 1 0 1 1
2 2 1 1 0 1
2 2 1 1 1 0.
Расстояние максимального координатного смещения между базовым нейроном 1 и нейронами 2, 3 и 4 равно 1, поскольку они находятся в окрестности 1, а расстояние между базовым нейроном и нейронами 5 и 6 равно 2, и они находятся в окрестности 2. Расстояние максимального координатного смещения от нейронов 3 и 4 до всех других нейронов равно 1.
Определим другое расстояние между нейронами, которое учитывает то количество связей, которое необходимо установить, чтобы задать путь движения от базового нейрона. Если задано  нейронов, положение которых определяется векторами нейронов, положение которых определяется векторами  , i = 1,..., S, то расстояние связи между ними определяется соотношением: , i = 1,..., S, то расстояние связи между ними определяется соотношением:
 (3.11) (3.11)
Если евклидово расстояние между нейронами меньше или равно 1, то расстояние связи принимается равным 1; если между нейронами с номерами i и j имеется единственный промежуточный нейрон с номером  , то расстояние связи равно 2, и т. д. , то расстояние связи равно 2, и т. д.
Для вычисления расстояния связи в ППП NNT предназначена функции linkdist. Для конфигурации нейронов, доказанной на рисунке 3.6, эти расстояния равны:
pos = gridtop{2,3)
d = linkdist(pos)
d =
0 1 1 2 2 3
1 0 2 1 3 2
1 2 0 1 1 2
2 1 1 0 2 1
2 3 1 2 0 1
3 2 2 1 1 0.
Расстояние связи между базовым нейроном 1 и нейронами 2, 3 равно 1, между базовым нейроном и нейронами 4 и 5 равно 2, между базовым нейроном и нейроном 6 равно 3. Наконец, определим расстояние максимального координатного смещении по формуле:
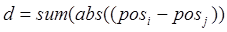 , (3.12) , (3.12)
где  , , 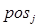 - векторы расположения нейронов с номерами i и j. - векторы расположения нейронов с номерами i и j.
Для вычисления расстояния максимального координатного смещения в ППП NNT предназначена функции mandist.
Вновь обратимся к конфигурации нейронов на рисунке 3.6:
pos = gridtop(2,3)
d = mandist(pos)
d =
0 1 1 2 2 3
1 0 2 1 3 2
1 2 0 1 1 2
2 1 1 0 2 1
2 3 1 2 0 1
3 2 2 1 1 0.
В случае прямоугольной сетки оно совпадает с расстоянием связи.
3.2.3 Архитектура сети
Промоделированная архитектура самоорганизующейся карты Кохонена в MATLABNNT показана на рисунке 3.10.

Рисунок 3.10 – Архитектура самоорганизующейся карты Кохонена
Эта архитектура аналогична структуре слоя Кохонена за исключением того, что здесь не используются смещения. Конкурирующая функция активации возвращает 1 для элемента выхода  , соответствующего победившему нейрону; все другие элементы вектора , соответствующего победившему нейрону; все другие элементы вектора  равны 0. равны 0.
Однако в сети Кохонена выполняется перераспределение нейронов, соседствующих с победившим нейроном. При этом можно выбирать различные топологии размещения нейронов и различные меры для вычисления расстояний между нейронами.
3.2.4 Создание сети
Для создания самоорганизующейся карты Кохонена в составе ППП MATLAB NNT предусмотрена М-функция newsom. Допустим, что требуется создать сеть для обработки двухэлементных векторов входа с диапазоном изменения элементов от 0 до 2 и от 0 до 1 соответственно. Предполагается использовать гексагональную сетку размера 2x3. Тогда для формирования такой нейронной сети достаточно воспользоваться оператором:
net = newsom([0 2; 0 1], [2 3])
net.layers{l}
ans =
dimensions:[2 3]
distanceFcn:'linkdist'
distances:[6x6 double]
initFcn:'initwb'
netInputFcn:'netsum'
positions:[2x6 double]
size:6
topologyFcn:'hextop'
transferFcn:'compet'
userdata:[1x1 struct].
Из анализа характеристик этой сети следует, что она использует по умолчанию гексагональную топологию hextop и функцию расстояния linkdist.
Для обучения сети зададим следующие 12 двухэлементных векторов входа:
Р = [0.1 0.3 1.2 1.1 1.8 1.7 0.1 0.3 1.2 1.1 1.8 1.7; ...
0.2 0.1 0.3 0.1 0.3 0.2 1.8 1.8 1.9 1.9 1.7 1.8].
Построим на топографической карте начальное расположение нейронов карты Кохонена и вершины векторов входа (рисунок 3.11):
plotsom(net.iw{1,1}, net.layers{1}.distances)
hold on
plot(P(1,;),P(2,:), '*к','markersize',10)
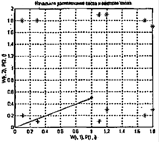
Рисунок 3.11 – Начальное расположение нейронов
Векторы входа помечены символом * и расположены по периметру рисунка, а начальное расположение нейронов соответствует точке с координатами (1, 0.5).
3.2.5 Обучение сети
Обучение самоорганизующейся карты Кохонена реализуется повекторно независимо от того, выполняется обучение сети с помощью функции trainwbl или адаптация с помощью функции adaptwb. В любом случае функция learnsom выполняет настройку элементов весовых векторов нейронов.
Прежде всего определяется нейрон-победитель и корректируются его вектор весов и векторы весов соседних нейронов согласно соотношению:
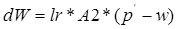 , (3.13) , (3.13)
где 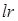 - параметр скорости обучения; - параметр скорости обучения;  - массив параметров соседства для нейронов, расположенных в окрестности нейрона-победителя i, который вычисляется по соотношению: - массив параметров соседства для нейронов, расположенных в окрестности нейрона-победителя i, который вычисляется по соотношению:
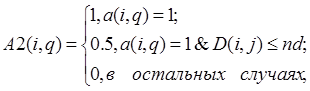 (3.14) (3.14)
где 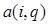 - элемент выхода нейронной сети; - элемент выхода нейронной сети;  - расстояние между нейронами i и j; - расстояние между нейронами i и j; 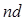 - размер окрестности нейрона-победителя. - размер окрестности нейрона-победителя.
Весовые векторы нейрона-победителя и соседних нейронов изменяются в зависимости от значения параметра соседства. Веса нейрона-победителя изменяются пропорционально параметру скорости обучения, а веса соседних нейронов - пропорционально половинному значению этого параметра.
Процесс обучения карты Кохонена включает 2 этапа: этап упорядочения векторов весовых коэффициентов в пространстве признаков и этап подстройки. При этом используются следующие параметры обучения сети (таблица 2.1):
Таблица 2.1
Параметры обучения сети
| Параметры обучения и настройки карты Кохонена |
Значение по умолчанию |
| Количество циклов обучения |
neе.trainParamepochs |
N |
>1000 |
| Количество циклов на этапе упорядочения |
netinputWeights{1,1}.learnParam.order_steps |
S |
1000 |
| Параметр скорости обучения на этапе упорядочения |
net.inputWeights{1,1}.leamParam.order_lr |
order_lr |
0.9 |
| Параметр скорости обучения на этапе подстройки |
net.inputWeights{1,1}.learnParam.tune_lr |
tune |
0.02 |
| Размер окрестности на этапе подстройки |
net.inputWeights(1,1).learnParam.tune_nd |
tune_nd |
1 |
В процессе построения карты Кохонена изменяются 2 параметра: размер окрестности и параметр скорости обучения.
Этап упорядочения. На этом этапе используется фиксированное количество шагов. Начальный размер окрестности назначается равным максимальному расстоянию между нейронами для выбранной топологии и затем уменьшается до величины, используемой на этапе подстройки в соответствии со следующим правилом:
 , (3.15) , (3.15)
где 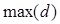 - максимальное расстояние между нейронами; - максимальное расстояние между нейронами;  - номер текущего шага. - номер текущего шага.
Параметр скорости обучения изменяется по правилу:
 . (3.16) . (3.16)
Таким образом, он уменьшается от значения order_lr до значения tune_lr.
Этап подстройки. Этот этап продолжается в течение оставшейся части процедуры обучения. Размер окрестности на этом этапе остается постоянным и равным:
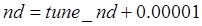 . (3.17) . (3.17)
Параметр скорости обучения изменяется по следующему правилу:
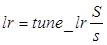 . (3.18) . (3.18)
Параметр скорости обучения продолжает уменьшаться, но очень медленно, и именно поэтому этот этап именуется подстройкой. Малое значение окрестности и медленное уменьшение параметра скорости обучения хорошо настраивают сеть при сохранении размещения, найденного на предыдущем этапе. Число шагов на этапе подстройки должно значительно превышать число шагов на этапе размещения. На этом этапе происходит тонкая настройка весов нейронов по отношению к набору векторов входа.
Как и в случае слоя Кохонена, нейроны карты Кохонена будут упорядочиваться так, чтобы при равномерной плотности векторов входа нейроны карты Кохонена также были распределены равномерно. Если векторы входа распределены неравномерно, то и нейроны на карте Кохонена будут иметь тенденцию распределяться в соответствии с плотностью размещения векторов входа.
Таким образом, при обучении карты Кохонена решается не только задача кластеризации входных векторов, но и выполняется частичная классификация.
Выполним обучение карты Кохонена размера 2x3 с гексагональной сеткой и с мерой, определяемой расстоянием связи:
net = newsom([0 2; 0 1], [2 3]).
Для обучения сети зададим 12 двухэлементных векторов входа
Р = [0.1 0.3 1.2 1.1 1.8 1.7 0.1 0.3 1.2 1.1 1.8 1.7; ...
0.2 0.1 0.3 0.1 0.3 0,2 1,8 1.8 1.9 1.9 1.7 1.8].
Зададим количество циклов обучения равным 2000:
net.trainParam.epochs = 2000
net.trainParam.show = 100
net = train (net, P)
plot(p(l,:),P(2,:), '*', 'markersize',10)
hold on
plotsom(net.iw{1*1},net.layers{l).distances).
Результат обучения представлен на рисунке 3.12.
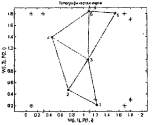
Рисунок 3.12 – Карты Кохонена с гексагональной сеткой
Положение нейронов и их нумерация определяются массивом весовых векторов, который для данного примера имеет вид:
net.IW{l}
ans =
1.2163 0.20902
0.73242 0.46577
1.0645 0.99103
0.4551 1.3893
1.5359 1.8079
1.0888 1.8433.
Если промоделировать карту Кохонена на массиве обучающих векторов входа, то будет получен следующий выход сети:
а = sim(net,P)
а =
(2,1)1
(2,2)1
(1,3) 1
(1,4) 1
(1,5) 1
(1,6) 1
(4,7) 1
(4,8) 1
(6,9) 1(6.10) 1
(5.11) 1
(5.12) 1.
Это означает, что векторы входов 1 и 2 отнесены к кластеру с номером 2, векторы 3-6 - к кластеру 1, векторы 7-8 - к кластеру 4, векторы 9-10 - к кластеру 6, а векторы 11-12 - к кластеру 5. Номер кластера на рисунке соответствует номеру соответствующего нейрона на карте Кохонена.
Если сформировать произвольный вектор входа, то карта Кохонена должна указать его принадлежность к тому или иному кластеру:
а = sim(net,[1.5; 1])
а = (3,1) 1.
В данном случае представленный вектор входа отнесен к кластеру с номером 3. Обратите внимание, что векторов такого сорта в обучающей последовательности не было. Рассмотрим еще 2 модели одномерной и двумерной карт Кохонена.
3.2.6 Моделирование одномерной карты Кохонена
Рассмотрим 100 двухэлементных входных векторов единичной длины, распределенных равномерно в пределах от 0 до 90°:
angles = 0:0.5*pi/99:0.5*pi
Р = [sin(angles);cos(angles)]
plot(P(1,1:10:end), P(2,l:10:end), 'b')
holdon.
График входных векторов приведен на рисунке 3.13, а, и на нем символом * отмечено положение каждого 10-го вектора.
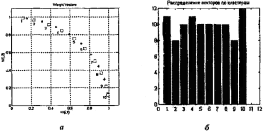
Рисунок 3.13 – График входных векторов
Сформируем самоорганизующуюся карту Кохонена в виде одномерного слоя из 10 нейронов и выполним обучение в течение 2000 циклов:
net = newsom( [0 1;0 1], [10])
net.trainParam.epochs = 2000; net.trainParam.show = 100
[net, tr] = train(net,P)
plotsom (net .IW{1,1}, net.layers{1}.distances) % (рисунок 3.13 ,a)
figure ( 2) a = sim(net,P); bar(sum(a1)) % (рисунок 3.13,б).
Весовые коэффициенты нейронов, определяющих центры кластеров, отмечены на рисунке 3.13, а цифрами. На рисунке 3.13, б показано распределение обучающих векторов по кластерам. Как и ожидалось, они распределены практически равномерно с разбросом от 8 до 12 векторов в кластере.
Таким образом, сеть подготовлена к кластеризации входных векторов. Определим, к какому кластеру будет отнесен вектор [1; 0]:
а = sim(net,[1;0])
а = (10,1)1.
Как и следовало ожидать, он отнесен к кластеру с номером 10.
3.2.7 Моделирование двумерной карты Кохонена
Этот пример демонстрирует обучение двумерной карты Кохонена. Сначала создадим обучающий набор случайных двумерных векторов, элементы которых распределены по равномерному закону в интервале [-1, 1]:
P = rands(2,1000)
plot(P(l,:),Р(2, :),'+') % (рисунок 3.14).

Рисунок 3.14 – Обучающий набор случайных двумерных векторов
Для кластеризации векторов входа создадим самоорганизующуюся карту Кохонена размера 5x6 с 30 нейронами, размещенными на гексагональной сетке:
net = newsom([-1 1; -1 1],[5,6])
net.trainParam.epochs = 1000
net.trainParam.show = 100
net = train(net,P); plotsom(net.IW{1,1},net.layers{l}.distances).
Результирующая карта после этапа размещения показана на рисунке 3.15, а. Продолжим обучение и зафиксируем карту после 1000 шагов этапа подстройки (рисунок 3.15, б), а затем после 4000 шагов (рисунок 3.15, в). Нетрудно убедиться, что нейроны карты весьма равномерно покрывают область векторов входа.

Рисунок 3.15 – Результирующая карта после этапа размещения
Определим принадлежность нового вектора к одному из кластеров карты Кохонена и построим соответствующую вершину вектора на рисунке 3.15, в:
а = sim(net,[0.5;0.3])
а = (19.1) 1
hold on, plot(0.5,0.3,'*k') %(риcунок 3.15, в).
Нетрудно убедиться, что вектор отнесен к 19-му кластеру.
Промоделируем обученную карту Кохонена, используя массив векторов входа:
а = sim(net,P)
bar(sum(a')) % (рисунок 3.16).
Из анализа рисунка 3.16 следует, что количество векторов входной последовательности отнесенных к определенному кластеру, колеблется от 13 до 50.

Рисунок 3.16 – Промоделированная карта Кохонена
Таким образом, в процессе обучения двумерная самоорганизующаяся карта Кохонена выполнила кластеризацию массива векторов входа. Следует отметить, что на этапе размещения было выполнено лишь 20% от общего числа шагов обучения, т, е. 80% общего времени обучения связано с тонкой подстройкой весовых векторов. Фактически на этом этапе выполняется в определенной степени классификация входных векторов.
Слой нейронов карты Кохонена можно представлять, в виде гибкой сетки, которая натянута на пространство входных векторов. В процессе обучения карты, в отличие от обучения слоя Кохонена, участвуют соседи нейрона-победителя, и, таким образом, топологическая карта выглядит более упорядоченной, чем области кластеризации слоя Кохонена.
ВЫВОДЫ
Современный мир переполнен различными данными и информацией - прогнозами погод, процентами продаж, финансовыми показателями и массой других. Часто возникают задачи анализа данных, которые с трудом можно представить в математической числовой форме. Например, когда нужно извлечь данные, принципы отбора которых заданы неопределенно: выделить надежных партнеров, определить перспективный товар, проверить кредитоспособность клиентов или надежность банков и т.п. И для того, чтобы получить максимально точные результаты решения этих задач необходимо использовать различные методы анализа данных.
Одним из ведущих методов анализа данных является кластеризация. Задачей кластеризации является разбиения совокупности объектов на однородные группы (кластеры или классы), а целью - поиск существующих структур. Решается данная задача при помощи различных методов, выбор метода должен базироваться на исследовании исходного набора данных. Сложностью кластеризации является необходимость ее экспертной оценки.
На данный момент существует большое количество методов кластеризации. Так, например, наиболее очевидным является применение методов математической статистики. Но тут возникает проблема с количеством данных, ибо статистические методы хорошо работают при большом объеме априорных данных, а у нас может быть ограниченное их количество. Поэтому статистические методы не могут гарантировать успешный результат, что делает их малоэффективными в решении многих практических задач.
Другим путем решения этой задачи может быть применение нейронных сетей, что является наиболее перспективным подходом. Можно выделить ряд преимуществ использования нейронных сетей:
·возможно построение удовлетворительной модели на нейронных сетях даже в условиях неполноты данных;
·искусственные нейронные сети легко работают в распределенных системах с большой параллелизацией в силу своей природы;
·поскольку искусственные нейронные сети подстраивают свои весовые коэффициенты, основываясь на исходных данных, это помогает сделать выбор значимых характеристик менее субъективным.
Кластеризация является задачей, относящейся к стратегии "обучение без учителя", т.е. не требует наличия значения целевых переменных в обучающей выборке. Для нейросетевой кластеризации данных могут использоваться различные модели сетей, но наиболее эффективным является использование сетей Кохонена или самоорганизующихся карт.
В данной магистерской работе подробно на примерах рассмотрена такая парадигма нейронных сетей как карты Кохонена. Основное отличие этих сетей от других моделей состоит в наглядности и удобстве использования. Эти сети позволяют упростить многомерную структуру, их можно считать одним из методов проецирования многомерного пространства в пространство с более низкой размерностью. Интенсивность цвета в определенной точке карты определяется данными, которые туда попали: ячейки с минимальными значениями изображаются темно-синим цветом, ячейки с максимальными значениями - красным.
Другое принципиальное отличие карт Кохонена от других моделей нейронных сетей - иной подход к обучению, а именно - неуправляемое или неконтролируемое обучение. Этот тип обучения позволяет данным обучающей выборки содержать значения только входных переменных. Сеть Кохонена учится понимать саму структуру данных и решает задачу кластеризации.
ПЕРЕЧЕНЬ ССЫЛОК
1. Руденко О.Г., Бодянский Е.В. Искусственные нейронные сети – Харьков, 2005. – 407с.
2. Котов А., Красильников Н. Кластеризация данных
3. Jain A.K., Murty M.N., Flynn P.J. Data Clustering: A Review "(http://www/csee/umbc/edu/nicolas/clustering/p264-jain.pdf)
4. Kogan J., Nicholas C., Teboulle M. Clustering Large and High Dimensional Data (http://www/csee/umbc/edu/nicolas/clustering/tutorial.pdf)
5. Медведев В.С., Потемкин В.Г. Нейронные сети. MATLAB 6 – М.: ДИАЛОГ-МИФИ, 2002. – 496с.
6. Круглов В. В., Борисов В. В. Искусственные нейронные сети. Теория и практика – М.: Горячая линия - Телеком, 2001. – 382с.
7. Каллан Р. Основные концепции нейронных сетей – «Вильямс», 2001. –288с.
|