Вступ
Тема контрольної роботи «Актуарні розрахунки» з дисципліни «Страхування».
Страхування – це відносини по захисту майнових інтересів громадян і юридичних осіб при настанні окремих не передбачуваних несприятливих подій за рахунок грошових фондів, що формуються шляхом сплати ними страхових платежів (страхових внесків, страхових премій). Іншими словами, категорія страхування визначає систему економічних відносин, що включає сукупність форм і методів формування цільових фондів грошових коштів і використання їх на відшкодування збитку при різних непередбачених несприятливих явищах (ризиках), а також на надання допомоги громадянам при настанні окремих визначених подій у їхньому житті.
З погляду права страхування відноситься до цивільно-правових відносин.
Специфічні ознаки страхування:
– відносини формуються при наявності імовірності настання непередбачених,раптових, несприятливих подій, що можуть викликати матеріальний збиток;
– при формуванні відносин здійснюється розподіл можливого збитку між учасниками страхування за рахунок того, що випадковий характер подій робить їх малоймовірними для всіх учасників одночасно;
– страхування передбачає перерозподіл збитку, як між учасниками, так і в часі;
– замкнута розкладка збитку обумовлює зворотність коштів, мобілізованих у страховий фонд: уся сума страхових платежів (без обліку витрат організацій, що здійснюють страхування) повертається у формі відшкодування збитку на протязі прийнятого в розрахунок інтервалу часу в тому ж самому територіальному масштабі.
Сутність страхування полягає в розподілі збитку між усіма ділянками страхування. Це є кооперацією по боротьбі з наслідками стихійних лих і протиріччями, що виникають у суспільстві через розходження майнових інтересів людей. Таким чином, страхування – елемент виробничих відносин. Воно пов’язано з відшкодуванням матеріальних втрат, що є основою для безперервності і безперебійності процесу відтворення.
Страхування – одна з найдавніших категорій суспільно-виробничих відносин. По мірі розвитку товарно-грошових відносин примітивна форма – натуральне страхування – була замінена грошовою формою. Страхові відносини, закріплені в письмовому договорі страхування як цивільно-правова угода, відомі, принаймні, з епохи пізнього Середньовіччя. Тоді завдяки великим географічним відкриттям помітно розширилися обсяги морської міжнародної торгівлі. Підприємцям знадобилися великі капітали, щоб використовувати нові можливості, що відкрилися.
Історично виникнувши в зв’язку з необхідністю забезпечити компенсації збитків, які не підлягають перекладанню на інших осіб, страхування перетерпіло в ході свого тривалого розвитку істотні зміни і поширюється зараз на багато випадків, коли настання збитків пов’язане з цивільно-правовою відповідальністю їх носія. У таких випадках страхування є для потерпілого додатковою гарантією охорони його майнових інтересів. Надалі, поряд з майновим страхуванням, що забезпечує відшкодування збитків, пов’язаних з втратою чи ушкодженням матеріальних благ, з’явилося особисте страхування, що гарантує виплати визначених грошових сум при настанні смерті, каліцтва, хвороби та при дожитті до визначеного віку людини.
1. Поняття і зміст актуарних розрахунків
Актуарні розрахунки – це сукупність економіко-математичних методів розрахунку необхідного і достатнього обсягу ресурсів страхового фонду страховика. В основі актуарних розрахунків лежить використання чинності закону великих чисел. Актуарними розрахунками в Україні можуть займатися особи, що мають відповідну кваліфікацію відповідно до вимог Держкомісії з регулювання ринків з фінансових послуг, що підтверджується відповідними посвідченнями.
Актуарій(лат. actuaru, actuarmus
– скорописець, рахівник) – фахівець зі страхування, що займається розробкою науково обґрунтованих методів розрахунків тарифних ставок по довгостроковому страхуванню життя: розрахунків, зв’язаних з утворенням резервів страхових внесків, визначенням розмірів позичок, викупних сум і т.д.
Редуцирування – зменшення розміру первісної страхової суми за договором довготермінового страхування життя. Воно зв’язано з достроковим припиненням сплати місячних внесків, коли страхувальник має право на викупну суму.
Викупна сума – сума, що належить до виплати страхувальнику за довгостроковим договором страхування життя, на день припинення їм сплати місячних страхових внесків. Розмір викупної суми залежить від тривалості минулого періоду страхування і терміну, на який був укладений договір. Так при п’ятилітньому терміну страхування викупна сума через 6 місяців страхування складає 75% від резерву внесків, що утворився по договорі, а через 4 роки 6 місяців – 98,5%.
На основі актуарних розрахунків визначається частка участі страхувальника в створенні страхового фонду, робиться перерахунок страхових внесків при зміні умов договору страхування життя.
Актуарна калькуляція – форма, по якій робиться розрахунок собівартості і вартості послуг, що надаються страховиком страхувальнику. Актуарна калькуляція:
- дозволяє визначити страхові платежі за договором, що потребує вимір ризику, прийнятого страховиком;
- відображає суму витрат на ведення справи по обслуговуванню договорів страхування.
Актуарні розрахунки виробляються з урахуванням особливостей страхування.
До них відносяться:
1) події, що піддаються оцінці, носять ймовірний характер. Це відбивається на величині пред’явлених до сплати страхових внесків;
2) визначення собівартості послуги, що робиться страховиком страхувальнику, проводиться у відношенні всієї страхової сукупності;
3) необхідність виділення і визначення розмірів страхових резервів страховика;
4) прогнозування сторнування договорів страхування, оцінка їхньої величини;
5) дослідження норми позичкового відсотка і тенденцій його зміни в часі;
6) наявність повного чи часткового збитку, пов’язаного зі страховим випадком, що створює потребу зміни його розподілу в часі і просторі з допомогою спеціальних таблиць;
7) дотримання принципу рівноваги між страховими внесками страхувальника і страховим забезпеченням, наданим страховою компанією, завдяки отриманим страховим внескам;
8) виділення групи ризику в рамках даної страхової сукупності.
Задачі актуарних розрахунків:
Вивчення і класифікація ризиків по окремим ознакам (групам) у рамках страхової сукупності.
Розрахунок математичної імовірності настання страхового випадку, визначення частоти і ступеня ваги наслідків заподіяння збитку як окремих ризикових груп, так і в цілому по страховій сукупності.
Математичне обґрунтування необхідних витрат на організацію процесу страхування.
Дослідження процентної ставки при використанні страховиком зібраних страхових внесків як інвестиції і тенденцій її зміни в конкретному тимчасовому інтервалі та визначення залежності між процентною ставкою і величиною брутто-ставки.
На підставі актуарних розрахунків визначаються розміри тарифних ставок, що за допомогою довгострокових фінансових досліджень заздалегідь занижуються на суму доходу, що буде отриманий страховиком від використання акумульованих внесків страхувальників як інвестиції.
В актуарних розрахунках застосовується теорія імовірності, оскільки розміри тарифних ставок у першу чергу залежать від ступеня імовірності страхового випадку.
Поняття імовірності стосовно до страхового випадку характеризується двома особливостями:
1) імовірність установлюється шляхом підрахунку несприятливих подій для страхувальника і страховика (пожари, повені, крадіжки і т. п.);
2) при страхуванні є лише деяка кількість об’єктів, з яких окремі підвергаються страховому випадку.
Імовірність страхового випадку в майновому страхуванні відбиває частоту страхових випадків за попередній період, тобто відношення потерпілих від події об’єктів до їхньої загальної кількості.
Приклад 1
.
У даному районі за ряд років у середньому втратам піддається 100 будинків з 10000, відповідно імовірність страхового випадку складає 0,01.
Імовірність утрати працездатності від нещасливих випадків обчислюється на основі звітних даних підприємств та лікарень. В особистому страхуванні для визначення імовірності страхового випадку використовуються показники смертності і тривалості життя населення, обчислювальні по таблиці смертності. При цьому виробляється диференціація тарифних ставок за віком людей на підставі даних і прийомів демографії. На основі статистичних спостережень над смертністю населення обчислюється імовірність дожити і вмерти для осіб різного віку, на підставі якої створюється таблиця смертності (табл. 1).
Таблиця 1. Витяг з таблиці смертності
Вік,
років
|
Кількість осіб, що доживають до віку Х років |
Кількість умираючих при переході від віку Х до віку Х+1 років |
Імовірність вмерти на протязі наступного року життя |
Середня тривалість майбутнього життя |

|

|
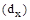
|
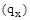
|
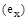
|
| 0 |
100000 |
1782 |
0,01782 |
69,57 |
| 1 |
98218 |
185 |
0,00188 |
69,83 |
| … |
… |
… |
… |
… |
| 20 |
96773 |
145 |
0,00149 |
51,73 |
| … |
… |
… |
… |
… |
| 40 |
92246 |
374 |
0,00406 |
33,71 |
| 41 |
91872 |
399 |
0,00434 |
32,84 |
| … |
… |
… |
… |
… |
| 50 |
87064 |
735 |
0,00844 |
25,38 |
| … |
… |
… |
… |
… |
| 60 |
77018 |
1340 |
0,01740 |
17,97 |
| іт.д. |
Таблиця смертності містить розрахункові показники, що характеризують смертність населення в окремих вікових групах і доживаємість при переході від одного віку до наступного. Вона показує, як поступово зменшується покоління одночасно народжених (прийняте за 100000 чол.) зі збільшенням віку.
Імовірність вмерти розраховується по формулі:
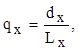
де 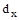 – число умираючих; – число умираючих;
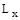 – число осіб, які доживають до даного віку. – число осіб, які доживають до даного віку.
Приклад 2
.
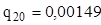 . .
Виходить, що з 100000 чоловік до 20-літнього віку не доживають 149 чоловік. Розташовуючи показниками імовірності вмерти, страховик з достатнім ступенем упевненості може припустити, що протягом найближчого року з числа застрахованих у віці 20 років може вмерти 0,15%, а імовірність дожити до 21 року складе:
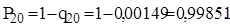
Розрахунок тарифної ставки (AR) включає визначення нетто-ставки, розмірів витрат на ведення справи, надбавки за ризик у майновому страхуванні і страхуванні відповідальності, знижки на позичковий відсоток у страхуванні життя і пенсій.
У розрахунках по особистому страхуванню надбавки за ризик можливі, але звичайно не використовуються. Це пов’язано з тим, що обсяг страхової сукупності досить великий, а страхова сума порівняно невелика.
Класифікація актуарних розрахунків
:
- по галузях страхування (особисте страхування, майнове, страхування відповідальності);
– за часом складання (планові і звітні);
– за ієрархічною ознакою: загальні (для всієї країни), зональні (для регіону), територіальні (для району).
Звітні актуарні розрахунки – це актуарні розрахунки, що розробляються по вже здійсненим операціям страховика, тобто по наявним звітним даним самого страховика.
Планові актуарні розрахунки розробляються при введенні нового виду страхування, по якому відсутні які-небудь достовірні спостереження ризику. У цьому випадку використовують результати актуарних розрахунків по однотипним чи близьким по змісту видам страхування. По закінченні визначеного терміну (не менш 3 років) аналізуються отримані статистичні дані по даному ризику й у плановий актуарний розрахунок вносяться відповідні корективи. Таким чином планові актуарні розрахунки перетворюються в звітні.
2. Основні показники страхової статистики
У процесі аналізу розраховують наступні показники:
- частота страхових подій;
- коефіцієнт кумуляції ризику;
- коефіцієнт збитковості;
- середня страхова сума на один об’єкт страховки;
- середня сума на один постраждалий об’єкт;
- вага ризику;
- збитковість страхової суми;
- норма збитковості;
- чистота збитку;
- вага збитку.
Частота страхових подій(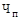 ) характеризується кількістю страхових подій у розрахунку на один об’єкт страхування: ) характеризується кількістю страхових подій у розрахунку на один об’єкт страхування:
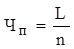 , ,
де L – число страхових подій;
n – число об’єктів страхування.
Частота не менше 1 означає, що одна страхова подія спричинила за собою кілька страхових випадків.
Коефіцієнт кумуляції – ризик чи спустошливість страхової події (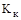 ) уявляє відношення числа постраждалих об’єктів до числа страхових подій: ) уявляє відношення числа постраждалих об’єктів до числа страхових подій:
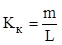 , ,
де m – число постраждалих об’єктів у результаті страхового випадку.
Кумуляція являє собою скупчення застрахованих об’єктів на обмеженому просторі (склад, судно). Коефіцієнт кумуляції ризику показує середнє число об’єктів, що постраждали від страхової події чи скільки застрахованих об’єктів може бути настигнуто страховою подією. Мінімальне значення 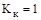 . Якщо . Якщо  , це означає, що в міру росту спустошливості зростає число страхових випадків на одну страхову подію. Отже, тому страховики намагаються уникати майнового страхування ризиків з великим , це означає, що в міру росту спустошливості зростає число страхових випадків на одну страхову подію. Отже, тому страховики намагаються уникати майнового страхування ризиків з великим 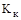 . .
Коефіцієнт збитковості (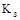 ) чи коефіцієнт збитку являє собою відношення суми виплаченого страхового відшкодування до суми всіх постраждалих об’єктів страхування: ) чи коефіцієнт збитку являє собою відношення суми виплаченого страхового відшкодування до суми всіх постраждалих об’єктів страхування:
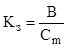 ,
,
де B – сума виплаченого страхового відшкодування;
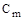 – страхова сума, що приходиться на ушкоджений об’єкт страхової сукупності. – страхова сума, що приходиться на ушкоджений об’єкт страхової сукупності.
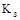 не може бути більше 1, що означає, що всі застраховані об’єкти знищені більш одного разу. не може бути більше 1, що означає, що всі застраховані об’єкти знищені більш одного разу.
Середня страхова сума на один об’єкт (договір) страхування являє собою відношення загальної страхової суми всіх об’єктів страхування до числа всіх об’єктів страхування:
 ,
,
де C – страхова сума всіх об’єктів страхування.
У зв’язку з тим, що об’єкти майнового страхування обов’язково розрізняються страховими сумами в актуарних розрахунках використовуються різні методи підрахунку середніх величин.
Середня страхова сума на один постраждалий об’єкт являє собою відношення страхової суми всіх постраждалих об’єктів до числа цих об’єктів:
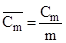 . .
Вага ризику (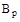 ) являє собою відношення середньої страхової суми на один постраждалий об’єкт до середньої страхової суми на один об’єкт страхування: ) являє собою відношення середньої страхової суми на один постраждалий об’єкт до середньої страхової суми на один об’єкт страхування:
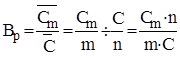 . .
Показник ваги ризику використовується при оцінці і переоцінці частоти прояву страхової події.
Збитковість страхової суми (імовірність збитку) являє собою відношення страхового відшкодування, яке належить до виплати, до страхової суми всіх об’єктів страхування:
 . .
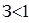 . У противному випадку маємо недострахування. Збитковість страхової суми можна розглядати як міру виплати фінансової премії. . У противному випадку маємо недострахування. Збитковість страхової суми можна розглядати як міру виплати фінансової премії.
Норма збитковості (коефіцієнт виплат) являє собою процентне відношення суми виплаченого страхового відшкодування до суми зібраних страхових внесків.
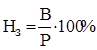 , ,
де P – сума зібраних страхових внесків.
Для практичних цілей обчислюють нетто-норму збитковості, брутто-норму збитковості. Норма збитковості може бути більше чи менше 100%.
Частота збитку обчислюється шляхом множення частоти страхових подій на коефіцієнт кумуляції:

чи
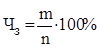 . .
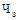 виражає частоту настання страхового випадку. Виражається звичайно в% чи промилє – тисячній частці числа виражає частоту настання страхового випадку. Виражається звичайно в% чи промилє – тисячній частці числа
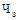 завжди менше 100%, тому що завжди менше 100%, тому що 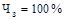 означає, що настання цієї події не імовірно, а дійсне для всіх об’єктів. означає, що настання цієї події не імовірно, а дійсне для всіх об’єктів.
Вага збитку (розмір збитку) являє собою добуток коефіцієнта збитковості і ваги ризику. Показує середню арифметичну величину збитку по ушкоджених об’єктах страхування стосовно середньої страхової суми всіх об’єктів:
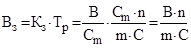 . .
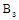 вказує на те, яка частина страхової суми знищена. Зі зростанням страхової суми вага збитку знижується. Показник вказує на те, яка частина страхової суми знищена. Зі зростанням страхової суми вага збитку знижується. Показник 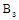 характеризує частковий збиток. У випадку, коли збиток дорівнює дійсній вартості застрахованого майна, такий збиток називається повним збитком. характеризує частковий збиток. У випадку, коли збиток дорівнює дійсній вартості застрахованого майна, такий збиток називається повним збитком.
3. Розрахунок тарифних ставок
При страхуванні відбувається замкнута розкладка збитку між страхувальниками. Тому при розрахунку нетто-ставки прийнято виходити з рівності:
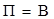 , ,
де П – страховий платіж, що відповідає нетто-ставці;
В-страхове відшкодування.
Страхова компанія повинна зібрати суму страхових внесків, що має бути потім виплачена страхувальникам.
Приклад 3
.
Імовірність страхового випадку (пожежі) у районі складає 0,01. За умови, що кожний з 100 об’єктів застрахований на 5000 грн. щорічні виплати складають:

Частка одного страхувальника в загальному страховому фонді складає 50 грн. (5000/100) – страховий внесок кожного страхувальника.
Нетто-ставка:
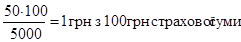 . .
На практиці при проведенні страхування суми виплачуваного страхового відшкодування постраждалим об’єктам, як правило, відрізняються від страхової суми по них. Причому, якщо за окремим договором виплата може бути тільки менше чи рівною страховій сумі, середня по групі об’єктів виплата на один договір може перевищувати середню страхову суму. Тому при розрахунку нетто-ставка коректується на коефіцієнт, який дорівнює відношенню середньої виплати до середньої страхової суми на один договір.
Нетто-ставка визначається за формулою:
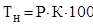 , ,
де 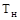 – тарифна нетто-ставка; – тарифна нетто-ставка;
Р – імовірність страхового випадку;
К – поправочний коефіцієнт;
100 – одиниця страхової суми (100 грн.).
 , ,
де 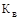 – кількість виплат (страхових випадків) за період (звичайний рік), грн.; – кількість виплат (страхових випадків) за період (звичайний рік), грн.;
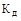 – кількість укладених договорів у даному році, од. – кількість укладених договорів у даному році, од.
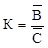 , ,
де 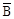 – середня виплата на один договір, грн.; – середня виплата на один договір, грн.;
 – середня страхова сума на один договір, грн. – середня страхова сума на один договір, грн.
Тоді розрахунок нетто-ставки можна проводити за формулою:
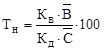 . .
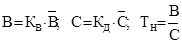 , ,
де В-загальна сума виплат страхового відшкодування, грн.;
С – загальна сума застрахованих об’єктів.
Тарифна ставка (брутто-ставка):
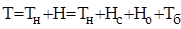 , ,
де Н – навантаження;
 – статті навантаження, встановлювані в абсолютній сумі; – статті навантаження, встановлювані в абсолютній сумі;
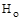 – статті навантаження, встановлювані у відсотку до брутто-ставки. – статті навантаження, встановлювані у відсотку до брутто-ставки.
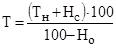 . .
Якщо всі елементи навантаження визначені у відсотках до брутто-ставки, то розмір брутто-ставки можна встановлювати за формулою:
 . .
Збитковість страхової суми може бути розрахована як по видах страхування, однорідним об’єктам страхування, так і по окремих страхових ризиках.
Страхові внески, зібрані страховиком, використовуються їм як інвестиції, що приносять визначений доход. Цей доход у сумі з внесками складе страховий фонд буде дорівнює:
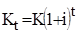 , ,
де 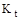 – сума страхового фонду, необхідна для виплати страхового відшкодування до кінця t періоду; – сума страхового фонду, необхідна для виплати страхового відшкодування до кінця t періоду;
К – первісна сума страхового фонду;
t – фактор часу.
З урахуванням доходів від вкладеного капіталу тарифні ставки в страхуванні життя заздалегідь занижуються на суму одержуваного доходу.
Сума первісного внеску:
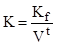 , ,
де V – множник, що дисконтує, (коефіцієнт дисконтування), визначений по спеціальній таблиці чи розрахований по формулі:
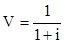 . .
Приклад 4
.
і = 0,40;
V10
(10 років) = 0,0346.
Отже, щоб через 10 років при і = 0,40 одержати 100 грн., необхідно сьогодні зробити внесок у 3 грн. 46 коп.
Тарифні ставки по страхуванню на дожиття бувають одноразові і річні
. Спочатку розраховують одноразову ставку.
Приклад 5
.
Зробити розрахунок брутто-ставки на дожиття за договором страхування людини у віці 50 років (х = 50) на термін 10 років (t = 10) зі страхової суми 100 грн. Частка навантаження в структурі тарифа 30% (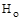 = 30%). = 30%).
Рішення.
1) Кількість виплат страхової суми через 10 років: з таблиці смертності за 60 років доживають 77018 чоловік, звідси кількість виплат – 77018.
2) Страховий фонд через 10 років: страхова сума з кожних 100 грн. договору
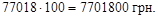
3) Первісна сума страхового фонду:
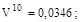
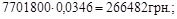

Отже, одноразовий загальний внесок – 266482 грн.
4) Внесок кожного страхувальника: по таблиці Х0
= 87064.
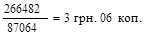
5) Брутто-ставка (тарифна ставка)
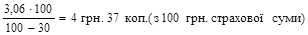 . .
Розрахунок річної тарифної ставки на дожиття (розстроченої по роках) обчислюється за формулою:
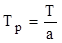 , ,
де Т – одноразова тарифна ставка (брутто-ставка);
а – коефіцієнт розстрочки.
Коефіцієнт розстрочки обчислюється з використанням таблиць смертності і дисконтуючих множників. Розрахунок здійснюється в спеціальних таблицях.
Приклад 6
.
При віці 50 років і терміну страхування 10 років – Кр
= 8,06; Тг
= 4,37/8,06 = 0,54 грн. Відповідно, річна тарифна ставка на дожиття складає 54 коп. з 100 грн. страхової суми.
Приклад 7
.
Розрахувати одноразову нетто-ставку по страхуванню на випадок смерті, якщо людина у віці 40 років страхується на термін 2 роки.
Рішення.
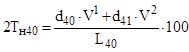 , ,
де 2 – термін страхування;
40 – вік страхувальника;
d40
– число осіб, що вмирають у віці 40 і 41 рік;
V1
, V2
– множники;
L – число оcіб у віці вступу в страхування;
100 – одиниця страхової суми.
d40
– 374, d41
– 399, L40
– 92246 чоловік (з таблиці смертності), при і – 0,4; V1
– 0,71433, V2
– 0,5102.
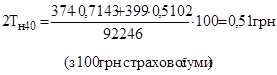
При визначенні тарифних ставок і резервів внесків по страхуванню життя для спрощення актуарних розрахунків використовують комутаційні числа.
Комутаційні числа – показники методу комутації (commutatіo
– зміна), тобто методу дослідження, що спирається на те, що при зміні одних показників проходить зміна в інших показниках.
В актуарних розрахунках по страхуванню життя застосовуються наступні комутаційні числа:
страхування актуарний розрахунок тарифний
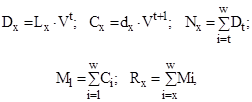
де x – вік;
t – фактор часу (термін страхування),
dx
– число умираючих при переході від віку х до віку х+1;
V – множник, що дисконтує;
Lx
– число осіб, що дожили до віку х;
і – процентна ставка позичкового капіталу;
w – граничний вік по таблиці смертності.
При розрахунку нетто-ставки на дожиття застосовуються числа Dx
і Nx,
на випадок смерті Cx
, Mx
, Nx
; при численні віку внесків у випадку смерті застрахованого – Rх
.
Існують спеціальні таблиці, де приводяться комутаційні числа при різних ставках.
Попередня формула в комутаційних числах має вид:
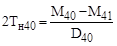 . .
Висновки
В процесі виконання контрольної роботи ми розкрили основні поняття і зміст актуарних розрахунків, основні показники страхової статистики, навчилися на ряді прикладів виконувати розрахунок тарифних ставок.
Література
1. Закон України «Про внесення змін до Закону України «Про страхування» // Урядовий кур’єр. – 2001. – 7 листопада.
2. Законодавство України про страхування // Збірник нормативних актів. – К.: Атіка, 2009. – 464 с.
3. Програма розвитку страхового ринку України на 2001–2004 роки. Затверджена Постановою KM України від 2 лютого 2001 р. №98. – К.: Офіційний вісник, 2001. – №5.
4. Александров А.А. Страхование. – М.: ПРИОР, 2008. – 186 с.
5. Балабанов И.Т., Балабанов А.И. Страхование. Учебник. – СПб.: Питер, 2001. – 256 с.
6. Бурроу К. Основы страховой статистики. – М.: Анкил, 2006. – 96 с.
7. Заруба О.Д. Страхова справа: Підручник. – К., 2008.
8. Касимов Ю.Ф. Начала актуарной математики. – Зелиноград: НТФ НИТ, 2004. –184 с.
9. Кутуков В.Б. Основы финансовой и страховой математики. Методы расчета кредитных, инвестиционных пенсионных и страховых схем. – М.:Дело, 2008. – 304 с.
10. Основы страховой деятельности: Учебник / Отв. ред. проф. Т.А. Федорова. – М.: БЕК, 2009. – 776 с.
11. Плешков А.П., Орлова И.В. Очерки зарубежного страхования. – М: Анкил, 2007. – 200 с.
12. Практикум по страховому делу / Под ред. проф. В.И. Рябикина. – М.: Финстатинформ, 2008. – 72 с.
13. Ротова Т.А., Руденко Л.С. Страхування: Навч. посібник. – К.: КНЕУ, 2001. – 400 с.
14. Рябикин В.И. Актуарные расчеты. – М.: Финстатинформ, 2006. – 89 с.
15. Страхування: Підручник / Керівник авт. колективу і наук, ред. С.С. Осадець. – Вид. 2-ге, перероб. і доп. – К.: КНЕУ, 2002. – 599 с.
16. Фалин Г.И., Фалин А.И. Введение в актуарную математику. Математические модели в страховании. – М.: Изд-во МГУ, 2004. – 110 с.
17. Шихов А.К. Страхование. Учеб. пособие для вузов. – М.: ЮНИТИ-ДАНА, 2000. –431 с.
18. Штрауб Э. Актуарная математика имущественного страхования. – М., 2004. –148 с.
|