ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Факультет автоматики и вычислительной техники
Информатика и вычислительная техника
Кафедра АИКС
АЛГОРИТМЫ ОБРАБОТКИ ДАННЫХ ЛИНЕЙНОЙ И НЕЛИНЕЙНОЙ СТРУКТУРЫ
Пояснительная записка к курсовому проекту
Студентка группы 8В84
А. C. Бушанова
Руководитель
Доцент каф. АИКС
И.В. Цапко
Томск – 2011г.
Задание на курсовое проектирование
Программно реализовать алгоритмы обработки данных, представленных в виде пирамиды (максимальной или минимальной – по выбору пользователя): преобразование массива в пирамиду, включение элемента в пирамиду, удаление элемента из пирамиды, вывод пирамиды на экран.
1. Краткое словесное описание алгоритмов, используемых при решении поставленной задачи
Пирамида - законченное бинарное дерево, имеющее упорядочение узлов по уровням.
Различают максимальные пирамиды и минимальные.
В максимальной пирамиде родительский узел больше или равен каждому из своих сыновей. Корень содержит наибольший элемент.
В минимальной пирамиде родительский узел меньше или равен каждому из своих сыновей.
Корень содержит наименьший элемент.
На каждом уровне пирамида содержит 2n
элементов, где n – номер уровня. Высота пирамиды  , где N — количество элементов пирамиды. , где N — количество элементов пирамиды.
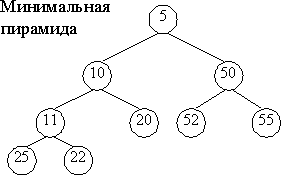

Пирамида используется в тех приложениях, где клиенту требуется прямой доступ к минимальному элементу.
Пирамида является списком, который хранит данные в виде бинарного дерева.
Все алгоритмы обработки пирамид сами должны обновлять дерево и поддерживать пирамидальное упорядочение.
Преобразование массива в пирамиду
Индекс последнего элемента пирамиды равен n-1.
Индекс его родителя равен (n-2)/2, и он определяет последний нелистовой узел пирамиды. Этот индекс является начальным для преобразования массива.
Рассмотрим целочисленный массив
int A[10] = {9, 12, 17, 30, 50, 20, 60, 65, 4, 19};
Индексы листьев: 5, 6, ..., 9.
Индексы родительских узлов: 4, 3, ..., 0.
Родитель А[4]=50, он больше своего сына А[9]=19 и поэтому должен поменяться с ним местами.
Родитель А[3]=30, он больше своего сына А[8]=4 и поэтому должен поменяться с ним местами (если меньших сына два, то меняется местами с наименьшим сыном).
На уровне 2 родитель А[2]=17 уже удовлетворяет условию пирамидальности, поэтому перестановок не производится.
Родитель А[1]=12 больше своего сына А[3]=4 и должен поменяться с ним местами.
Процесс прекращается в корневом узле. Родитель А[0]=9 должен поменяться местами со своим сыном А[1].
Результирующее дерево является пирамидой.

Включение элемента в пирамиду
1. Новый элемент добавляется в конец списка.
2. Если новый элемент имеет значение, меньшее, чем у его родителя, узлы меняются местами.
3. Новый родитель рассматривается как сын, и проверяется условие пирамидальности для более старшего родителя.
4. Процесс сканирует путь предков и завершается, встретив родителя, меньше чем новый элемент, или достигнув корневого узла.
Удаление из пирамиды
Данные удаляются всегда из корня дерева.
1. Удалить корневой узел и заменить его последним узлом.
2. Если новый корневой узел больше любого своего сына, то необходимо его поменять местами с наименьшим сыном.
3. Движение по пути меньших сыновей продолжается до тех пор, пока элемент не займет правильную позицию в качестве родителя или пока не будет достигнут конец списка.
2. Структурная схема программы с описанием
Схема взаимодействия функций программного комплекса:
      
   

Структурные схемы алгоритмов:
Преобразование массива в максимальную пирамиду
Функция удаления элемента из пирамиды

  

· программы, нажмите на кнопку “Program’s Data”. Вверху под надписью “Array” будет выведен массив.
· Если Вы желаете ввести данные самостоятельно, в поле над кнопками “Delete Element” и “Add Element”, введите число, затем нажмите кнопку “Add Element”, введенное число появится под надписью “Array”.
· Далее следует выбрать тип пирамиды, для этого установите метку напротив желаемой пирамиды, затем нажмите кнопку “Show Tree”. В поле слева от панели параметров вы увидите получившуюся пирамиду.
· Если Вы хотите добавить элемент в уже существующую пирамиду , в поле над кнопками “Delete Element” и “Add Element”, введите число, затем нажмите кнопку “Add Element”, введенное число будет добавлено в конец массива.
· Если вы хотите удалить элемент, введите его значение в поле над кнопками “Delete Element” и “Add Element” и нажмите кнопку “Delete Element”, если этот элемент является корнем, произойдет его удаление.
пирамида максимальный минимальный алгоритм
3. Пример выполнения программного комплекса

Рис. 1. Общий вид приложения

Рис. 2. Ввод данных и вывод пирамиды
Список используемой литературы
1. Цапко И.В. Структуры и алгоритмы обработки данных: учебное пособие Томск: Изд-во Томского политехнического университета, 2007. – 184 с.
Приложение А
Листинг программы
#include <vcl.h>
#pragma hdrstop
#include "UnitHeapTree.h"
#include <math.h>
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TFormHeapTree *FormHeapTree;
#define N 1000
//---------------------------------------------------------------------------
int array[N]; // используемый массив
int n=0; //фактическое количество элементов в массиве
//---------------------------------------------------------------------------
void makeArray() //создание массива, если пользователь
{ //предпочел использовать данные программы
randomize();
for(int i=0;i<10;i++)
array[i]=random(20);
n=10;
}
//-----------------функция преобразования массива в минимальную пирамиду -----------------
void heap_min()
{
int temp;
for(int l =floor((n-1)/2); l>=0; l--)
{
for(int j = floor((n-1)/2); j>=0; j--)
{
int i=2*j;
if((i+2)<n)
{
if(array[i+2]<=array[i+1] && array[i+2]<array[j])
{
temp = array[i+2];
array[i+2] = array[j];
array[j] = temp;
}
else
if(array[i+2]>=array[i+1] && array[i+1]<array[j])
{
temp = array[i+1];
array[i+1] = array[j];
array[j] = temp;
}
}
else
if(array[i+1]< array[j])
{
temp = array[i+1];
array[i+1] = array[j];
array[j] = temp;
}
}
}
}
//---------------функция преобразования массива в максимальную пирамиду -----------------
void heap_max()
{
int temp;
for(int l =floor((n-1)/2); l>=0; l--)
{
for(int j = floor((n-1)/2); j>=0; j--)
{
int i=2*j;
if((i+2)<n)
{
if(array[i+2]>=array[i+1] && array[i+2]>array[j])
{
temp = array[i+2];
array[i+2] = array[j];
array[j] = temp;
}
else
if(array[i+2]<=array[i+1] && array[i+1]>array[j])
{
temp = array[i+1];
array[i+1] = array[j];
array[j] = temp;
}
}
else
if(array[i+1]> array[j])
{
temp = array[i+1];
array[i+1] = array[j];
array[j] = temp;
}
}
}
}
//-------------------------удаление элемента из пирамиды ----------------------------------------
void delElem(int t)
{
int f;
for(int i=0; i<n; i++)
{
if(array[i]==t && i==0)
{
array[0]=array[n-1];
n=n-1;
break;
}
else
{
ShowMessage("This element is not a root or this element is not found");
break;
}
}
}
//-------------------функция очищения области рисования пирамиды -------------------------------
void Re(void)
{
FormHeapTree->ImageTree->Canvas->FillRect(Rect(0,0,FormHeapTree->ImageTree->Width,FormHeapTree->ImageTree->Height));
}
//-------------------------Функция вывода пирамиды на экран -------------------------------------------
void showTree()
{
Re();
int x = FormHeapTree->ImageTree->Width/2;
int y = 20;
int pr = 20;//расстояние между элементрами
if(n!=0)
{
int m = log(n)/log(2);
FormHeapTree->ImageTree->Canvas->Ellipse(x,20,x+30,50);
FormHeapTree->ImageTree->Canvas->TextOutA(x+10,y+5,array[0]);
//левое поддерово снизу вверх
for(int i=m; i>0; i--)
{
int q=pow(2,i-1)-1;
for(int j=pow(2,i)-1; j<=pow(2,i)+pow(2,i-1)-2; j++)
if(j<n)
{
FormHeapTree->ImageTree->Canvas->Ellipse(x-q*pr*2-pr-5, y+i*50-5, x-q*pr*2-pr+30-5, y+i*50-5+30);
FormHeapTree->ImageTree->Canvas->TextOutA(x-q*pr*2-pr+5, y+i*50, array[j]);
q--;
}
//правое поддерево
q=0;
for(int j = pow(2,i)+pow(2,i-1)-1; j<=pow(2,i+1)-2; j++)
if(j<n)
{
FormHeapTree->ImageTree->Canvas->Ellipse(x+q*pr*2+pr-5, y+i*50-5, x+q*pr*2+pr+30-5, y+i*50-5+30);
FormHeapTree->ImageTree->Canvas->TextOutA(x+q*pr*2+pr+5, y+i*50, array[j]);
q++;
}
pr*=2;
}
}
}
//---------------------------------------------------------------------------
__fastcall TFormHeapTree::TFormHeapTree(TComponent* Owner)
: TForm(Owner)
{
}
//---------------------------------функция вывода массива на экран ------------------------------------
void ShowArray()
{
FormHeapTree->LabelArray->Caption = "";
for(int i=0; i<n; i++)
FormHeapTree->LabelArray->Caption = FormHeapTree->LabelArray->Caption + " " + array[i];
}
//--------------------функция добавления элемента в пирамиду---------------------------------------
void __fastcall TFormHeapTree::SpeedButtonAddClick(TObject *Sender)
{
if(this->EditElem->Text != "")
{
try
{
int temp = StrToInt(this->EditElem->Text);
array[n] = temp;
this->LabelArray->Caption = this->LabelArray->Caption + " " + array[n];
n++;
}
catch(EConvertError &e)
{
ShowMessage("Please enter only numbers.");
}
}
else
ShowMessage("Please enter element!");
}
//----------------------функция непосредственно удаления элемента из пирамиды -----------
void __fastcall TFormHeapTree::SpeedButtonDeleteClick(TObject *Sender)
{
if(this->EditElem->Text != "")
{
try
{
int temp = StrToInt(this->EditElem->Text);
delElem(temp);
this->LabelArray->Caption = "";
ShowArray();
}
catch(EConvertError &e)
{
ShowMessage("Please enter only numbers.");
}
}
else
ShowMessage("Please enter element!");
}
//----------------- функция вывода пирамиды на экран ------------------------------------------------
void __fastcall TFormHeapTree::SpeedButtonShowTreeClick(TObject *Sender)
{
if(RadioButtonMin->Checked == true || RadioButtonMax->Checked == true)
{
if(RadioButtonMin->Checked)
{
// RadioButtonMax->Checked = false;
heap_min();
ShowArray();;
}
if(RadioButtonMax->Checked)
{
//RadioButtonMin->Checked = false;
heap_max();
ShowArray();
}
showTree();
}
else
ShowMessage("Please choose type of heap-tree.");
}
//------------ функция использоания данных программы-----------------------------------------------
void __fastcall TFormHeapTree::ButtonProgDataClick(TObject *Sender)
{
makeArray();
ShowArray();;
//---------------------------------------------------------------------------
|