Министерство образования Российской Федерации
Тульский государственный университет
Кафедра
Теоретической Механики
Решение типовых задач по теоретической механике
Выполнил: студент гр.220121
Батищев Д. В.
Проверил: Макарова Л. Л.
Тула 2004
1. K2. Поступательное и вращательное движение твердого тела
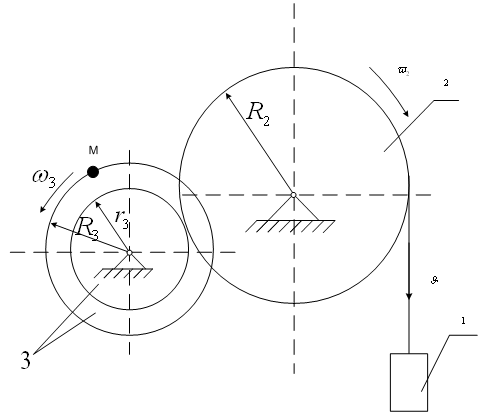
Дано:
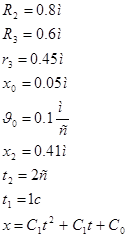
Определить: 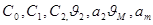
Решение
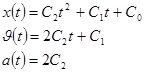
При 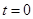
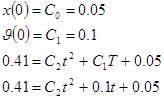
При 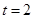
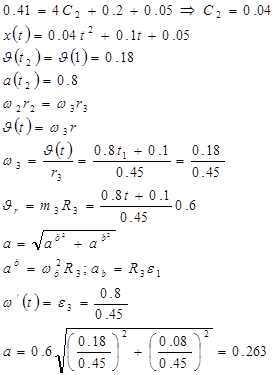
Ответ: 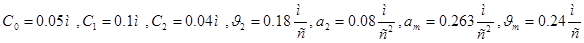
2. К3. Кинематический анализ плоского механизма
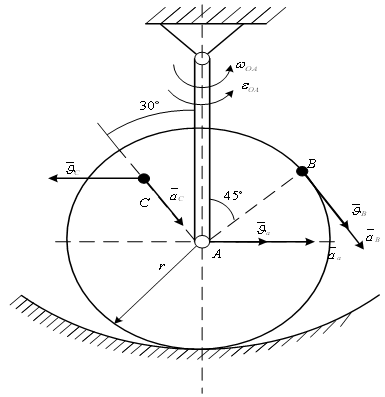
Дано:
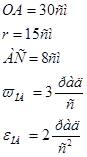
Найти:
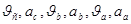
поступательный кинематический энергия твердый тело
Решение
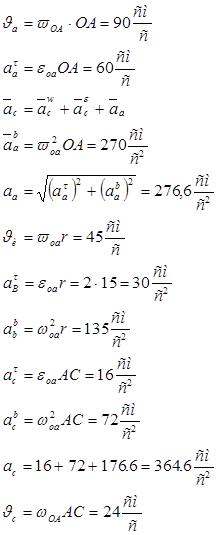
Ответ:
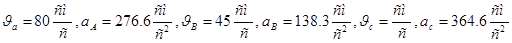
3. D10. Применение теоремы об изменении кинетической энергии к
изучению движения механической системы
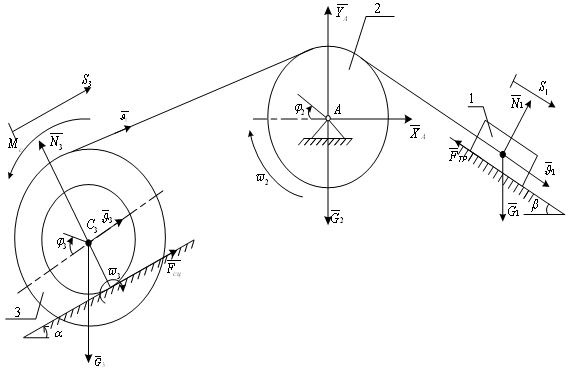
Дано:

Определить 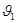 при при 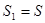
Решение
Применим теорему об изменении кинетической энергии системы:
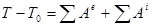
Рассматривая, система неизменяема, поэтому 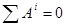 . Так как в начальном положении системы находится в покое, то . Так как в начальном положении системы находится в покое, то 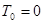 , тогда: , тогда:
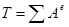
Составить кинетические соотношения:
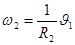
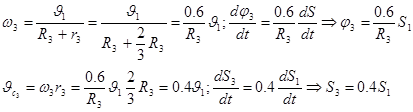
Вычислим кинетическую энергию системы в конечном положении:
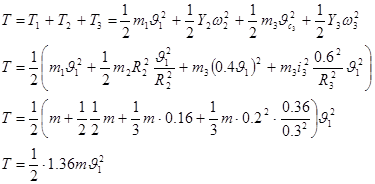
Найдем сумму работ всех внешних сил на заданном перемещении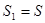 : :

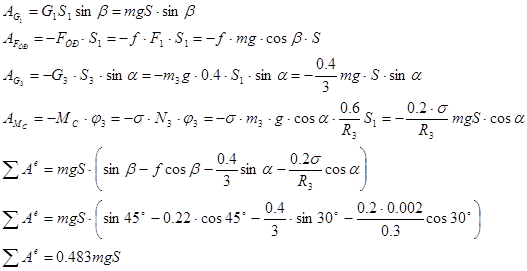
Для определения скорости 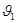 воспользуемся уравнением: воспользуемся уравнением: 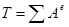
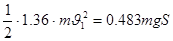 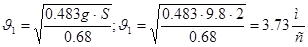
Ответ: 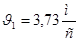
4. D19. Применение общего управления динамики к исследованию
движения механической системы с одной степенью свободы
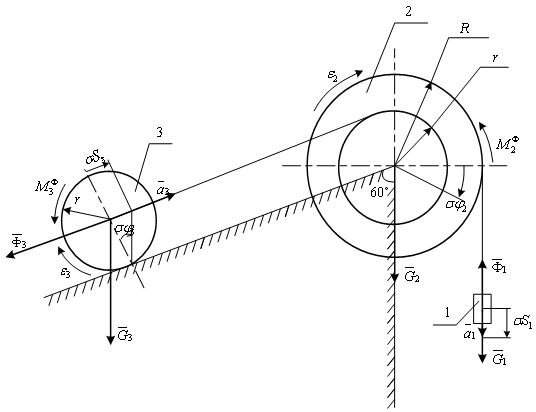
Дано:
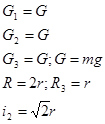
Определить: 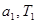
Решение:
Сообщим системе возможное перемещение в направлении ее действительного движения.
Составим общее уравнение динамики:
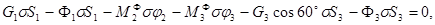
где 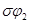 и и 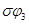 - углы поворотов блоков 2 и 3. - углы поворотов блоков 2 и 3.
Найдем зависимость между возможными перемещениями
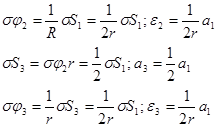
Определим силы и моменты сил инерции.
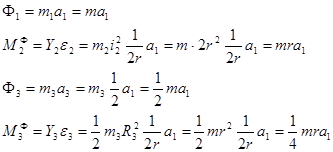
Подставляя полученное выражение в общее уравнение динамики, найдем ускорение груза 1.
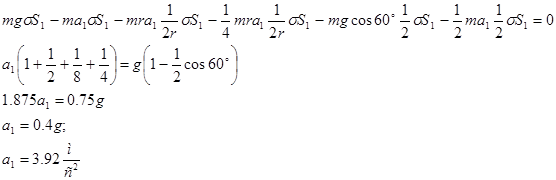
Для определения натяжения в ветви нити 1-2 мысленно разрежем нить и заменим её действие на груз 1 реакцией 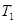 . На основании принципа Даламбера имеем: . На основании принципа Даламбера имеем:

Ответ: 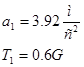
5. D14. Применение принципа возможных перемещений к решению
задач о равновесии сил
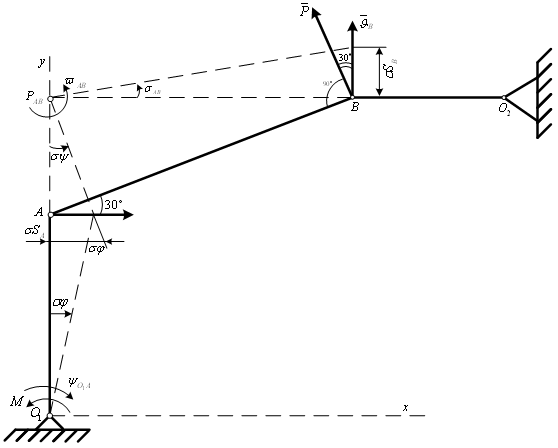
1. Составить уравнение работ, выражающее принцип возможных перемещений:
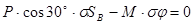
Найдем зависимость между возможными перемещениями:
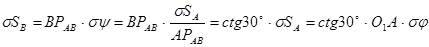
С учетом этого запишем:
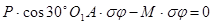
Отсюда: 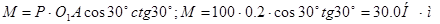
2. Составим уравнение мощностей, выражающие принцип возможных скоростей: 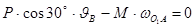
Запишем кинематическое соотношения:
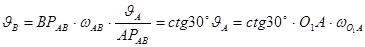
С учетом этого запишем:
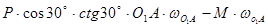
Отсюда находим: 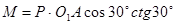
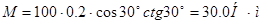
Ответ: 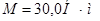
|