БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
РЕСПУБЛИКАНСКИЙ ИНСТИТУТ ИННОВАЦИОННЫХ ТЕХНОЛОГИЙ
КАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Курсовая работа
Дисциплина «Математическое моделирование»
Тема: «Моделирование движения парашютиста»
Минск 2008
Содержание
Введение
1. Свободное падение тела с учетом сопротивления среды
2. Формулировка математической модели и ее описание.
3. Описание программы исследования с помощью пакета Simulink
4. Решение задачи программным путем
Список использованных источников
Формулировка проблемы
:
Катапульта выбрасывает манекен человека с высоты 5000 метров. Парашют не раскрывается, манекен падает на землю. Оценить скорость падения в момент удара о землю. Оценить время достижения манекеном предельной скорости. Оценить высоту, на которой скорость достигла предельного значения. Построить соответствующие графики, провести анализ и сделать выводы.
Научиться составлять математическую модель, решать дифференциальные уравнения программными средствами (используется язык технических вычислений MatLAB 7.0, пакет расширения Simulink) и анализировать полученные данные о математической модели.
При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту, относительно несложную, задачу нельзя решить средствами “школьной” физики: таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления.
Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это утверждение не является абсолютным). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение, 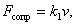 где где 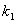 определяется свойствами среды и формой тела. Например, для шарика определяется свойствами среды и формой тела. Например, для шарика 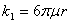 — это формула Стокса, где — это формула Стокса, где 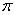 — динамическая вязкость среды, r — радиус шарика. Так, для воздуха при t = 20°С и давлении 1 атм — динамическая вязкость среды, r — радиус шарика. Так, для воздуха при t = 20°С и давлении 1 атм 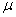 = 0,0182 H.c.м-2 для воды 1,002 H.c.м-2 , для глицерина 1480 H.c.м-2. = 0,0182 H.c.м-2 для воды 1,002 H.c.м-2 , для глицерина 1480 H.c.м-2.
Оценим, при какой скорости для падающего вертикально шара сила сопротивления сравняется с силой тяжести (в движение станет равномерным).
Имеем
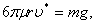
или
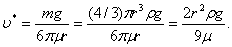 (1)
(1)
Пусть r= 0,1 м, 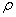 = 0,8 кг/м (дерево). При падении в воздухе = 0,8 кг/м (дерево). При падении в воздухе 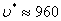 м/с, в воде м/с, в воде 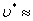 17 м/с, в глицерине 17 м/с, в глицерине 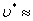 0,012 м/с. 0,012 м/с.
На самом деле первые два результата совершенно не соответствуют действительности. Дело в том, что уже при гораздо меньших скоростях сила сопротивления становится пропорциональной квадрату скорости: 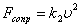 . Разумеется, линейная по скорости часть силы сопротивления формально также сохранится, но если . Разумеется, линейная по скорости часть силы сопротивления формально также сохранится, но если 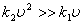 , то вкладом , то вкладом 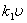 можно пренебречь (это конкретный пример ранжирования факторов). О величине k2 известно следующее: она пропорциональна площади сечения тела S, поперечного по отношению к потоку, и плотности среды можно пренебречь (это конкретный пример ранжирования факторов). О величине k2 известно следующее: она пропорциональна площади сечения тела S, поперечного по отношению к потоку, и плотности среды 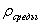 и зависит от формы тела. Обычно представляют k2 = 0,5сS и зависит от формы тела. Обычно представляют k2 = 0,5сS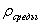 , где с — коэффициент лобового сопротивления — безразмерен. Некоторые значения с (для не очень больших скоростей) приведены на рис.1. , где с — коэффициент лобового сопротивления — безразмерен. Некоторые значения с (для не очень больших скоростей) приведены на рис.1.
При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом вихри газа или жидкости начинают интенсивно отрываться от тела, значение с в несколько раз уменьшается. Для шара оно становится приблизительно равным 0,1. Подробности можно найти в специальной литературе.
Вернемся к указанной выше оценке, исходя из квадратичной зависимости силы сопротивления от скорости.
Имеем
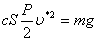
или
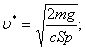 (2) (2)
для шарика
 (3)
(3)
 |
Диск
Полусфера
Полусфера
Шар
Каплевидное тело
Каплевидное тело
|
с = 1,11
с = 1,33
с = 0,55
с = 0,4
с = 0,045
с = 0,01
|
Рис
1
. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму
Примем r = 0,1 м, 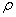 =0,8.103 кг/м3 (дерево). Тогда для движения в воздухе ( =0,8.103 кг/м3 (дерево). Тогда для движения в воздухе (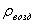 = 1,29 кг/м3 ) получаем = 1,29 кг/м3 ) получаем 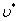 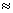 18 м/с, в воде( 18 м/с, в воде(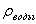 = 1.103 кг/м3 ) = 1.103 кг/м3 ) 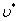 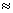 0,65 м/с, в глицерине ( 0,65 м/с, в глицерине (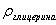 = 1,26.103 кг/м3 ) = 1,26.103 кг/м3 ) 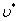 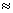 0,58 м/с. 0,58 м/с.
Сравнивая с приведенными выше оценками линейной части силы сопротивления, видим, что для движения в воздухе и в воде ее квадратичная часть сделает движение равномерным задолго до того, как это могла бы сделать линейная часть, а для очень вязкого глицерина справедливо обратное утверждение. Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения — уравнение второго закона Ньютона с учетом двух сил, действующих на тело: силы тяжести и силы сопротивления среды:
 (4)
(4)
Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем
 (5)
(5)
Вопрос, который мы будем обсуждать на первом этапе, таков: каков характер изменения скорости со временем, если все параметры, входящие в уравнение (7) заданы? При такой постановке модель носит сугубо дескриптивный характер. Из соображений здравого смысла ясно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого момента, 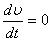 , и соответствующую установившуюся скорость , и соответствующую установившуюся скорость 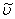 можно найти из условия можно найти из условия 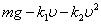 =0, решая не дифференциальное, а квадратное уравнение. Имеем =0, решая не дифференциальное, а квадратное уравнение. Имеем
 (6)
(6)
(второй — отрицательный — корень, естественно, отбрасываем). Итак, характер движения качественно таков: скорость при падении возрастает от 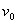 до до 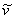 . Как и по какому закону – это можно узнать, лишь решив дифференциальное уравнение (7). . Как и по какому закону – это можно узнать, лишь решив дифференциальное уравнение (7).
Однако даже в столь простой задаче мы пришли к дифференциальному уравнению, которое не относится ни к одному из стандартных типов, выделяемых в учебниках по дифференциальным уравнениям, допускающих очевидным образом аналитическое решение. И хотя это не доказывает невозможность его аналитического решения путем хитроумных подстановок, но они не очевидны. Допустим, однако, что нам удастся найти такое решение, выраженное через суперпозицию нескольких алгебраических и трансцендентных функций – а как найти закон изменения во времени перемещения? Формальный ответ прост:
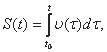 (7) (7)
но шансы на реализацию этой квадратуры уже совсем невелики. Дело в том, что класс привычных нам элементарных функций очень узок, и совершенно обычна ситуация, когда интеграл от суперпозиции элементарных функций не может быть выражен через элементарные функции в принципе. Математики давно расширили множество функций, с которыми можно работать почти так же просто, как с элементарными (т. е. находить значения, различные асимптотики, строить графики, дифференцировать, интегрировать). Тем, кто знаком с функциями Бесселя, Лежандра, интегральными функциями и еще двумя десятками других, так называемых специальных функций, легче находить аналитические решения задач моделирования, опирающихся на аппарат дифференциальных уравнений. Однако даже получение результата в виде формулы не снимает проблемы представления его в виде, максимально доступном для понимания, чувственного восприятия, ибо мало кто может, имея формулу, в которой сопряжены логарифмы, степени, корни, синусы и тем более специальные функции, детально представить себе описываемый ею процесс - а именно это есть цель моделирования.
В достижении этой цели компьютер — незаменимый помощник. Независимо от того, какой будет процедура получения решения - аналитической или численной, — задумаемся об удобных способах представления результатов. Разумеется, колонки чисел, которых проще всего добиться от компьютера (что при табулировании формулы, найденной аналитически, что в результате численного решения дифференциального уравнения), необходимы; следует лишь решить, в какой форме и размерах они удобны для восприятия. Слишком много чисел в колонке быть не должно, их трудно будет воспринимать, поэтому шаг, с которым заполняется таблица, вообще говоря, гораздо больше шага, с которым решается дифференциальное уравнение в случае численного интегрирования, т.е. далеко не все значения 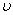 и и 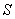 , найденные компьютером, следует записывать в результирующую таблицу (табл. 2). , найденные компьютером, следует записывать в результирующую таблицу (табл. 2).
Таблица 2
Зависимость перемещения и скорости падения от времени (от 0 до 15 с)
| t(c) |
S(m) |
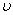 (м/с) (м/с) |
t(c) |
S(m) |
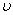 (м/с) (м/с) |
0
1
2
3
4
5
6
7
|
0
4.8
18.7
40.1
66.9
97.4
130.3
164.7
|
0
9,6
17,9
24,4
28,9
31,9
33,8
35,0
|
8
9
10
11
12
13
14
15
|
200.1
235.9
272.1
308.5
345.0
381.5
418.1
454.7
|
35.6
36.0
36.3
36.4
36.5
36.6
36.6
36.6
|
Кроме таблицы необходимы графики зависимостей 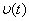 и и 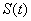 ; по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественное понимание процесса. ; по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественное понимание процесса.
Еще один элемент наглядности может внести изображение падающего тела через равные промежутки времени. Ясно, что при стабилизации скорости расстояния между изображениями станут равными. Можно прибегнуть и к цветовой раскраске — приему научной графики, описанному выше.
Наконец, можно запрограммировать звуковые сигналы, которые подаются через каждый фиксированный отрезок пути, пройденный телом — скажем, через каждый метр или каждые 100 метров — смотря по конкретным обстоятельствам. Надо выбрать интервал так, чтобы вначале сигналы были редкими, а потом, с ростом скорости, сигнал слышался все чаще, пока промежутки не сравняются. Таким образом, восприятию помогают элементы мультимедиа. Поле для фантазии здесь велико.
Приведем конкретный пример решения задачи о свободно падающем теле. Герой знаменитого фильма “Небесный тихоход” майор Булочкин, упав с высоты 6000 м в реку без парашюта, не только остался жив, но даже смог снова летать. Попробуем понять, возможно, ли такое на самом деле или же подобное случается только в кино. Учитывая сказанное выше о математическом характере задачи, выберем путь численного моделирования. Итак, математическая модель выражается системой дифференциальных уравнений.
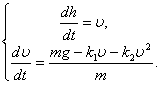 (8)
(8)
Разумеется, это не только абстрактное выражение обсуждаемой физической ситуации, но и сильно идеализированное, т.е. ранжирование факторов перед построением математической модели произведено. Обсудим, нельзя ли произвести дополнительное ранжирование уже в рамках самой математической модели с учетом конкретно решаемой задачи, а именно — будет ли влиять на полет парашютиста линейная часть силы сопротивления и стоит ли ее учитывать при моделировании.
Так как постановка задачи должна быть конкретной, мы примем соглашение, каким образом падает человек. Он опытный летчик и наверняка совершал раньше прыжки с парашютом, поэтому, стремясь уменьшить скорость, он падает не “солдатиком”, а лицом вниз, “лежа”, раскинув руки в стороны. Рост человека возьмем средний — 1,7 м, а полуобхват грудной клетки выберем в качестве характерного расстояния — это приблизительно 0,4 м. для оценки порядка величины линейной составляющей силы сопротивления воспользуемся формулой Стокса. Для оценки квадратичной составляющей силы сопротивления мы должны определиться со значениями коэффициента лобового сопротивления и площадью тела. Выберем в качестве коэффициента число с=1,2 как среднее между коэффициентами для диска и для полусферы (выбор дня качественной оценки правдоподобен). Оценим площадь: S = 1,7 ∙ 0,4 = 0,7(м2).
В физических задачах на движение фундаментальную роль играет второй закон Ньютона. Он гласит, что ускорение, с которым движется тело, прямо пропорционально действующей на него силе (если их несколько, то равнодействующей, т.е. векторной сумме сил) и обратно пропорционально его массе:
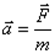 . .
Так для свободно падающего тела под действием только собственной массы закон Ньютона примет вид:
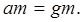
Или в дифференциальном виде:
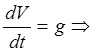
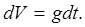
Взяв интеграл от этого выражения, получим зависимость скорости от времени:
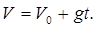
Если в начальный момент V0 = 0, тогда 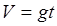 . .
Далее определим зависимость высоты от времени, для чего проинтегрируем последнее выражение.
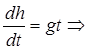
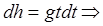
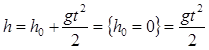 . .
Выясним, при какой скорости сравняются линейная и квадратичная составляющие силы сопротивления. Обозначим эту скорость 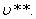 Тогда Тогда

или

Ясно, что практически с самого начала скорость падения майора Булочкина гораздо больше, и поэтому линейной составляющей силы сопротивления можно пренебречь, оставив лишь квадратичную составляющую.
После оценки всех параметров можно приступить к численному решению задачи. При этом следует воспользоваться любым из известных методов интегрирования систем обыкновенных дифференциальных уравнений: методом Эйлера, одним из методов группы Рунге — Кутта или одним из многочисленных неявных методов. Разумеется, у них разная устойчивость, эффективность и т.д. — эти сугубо математические проблемы здесь не обсуждаются.
Вычисления производятся до тех пор, пока не опустится на воду. Примерно через 15 с после начала полета скорость становится постоянной и остается такой до приземления. Отметим, что в рассматриваемой ситуации сопротивление воздуха радикально меняет характер движения. При отказе от его учета график скорости, изображенный на рисунке 2, заменился бы касательной к нему в начале координат.
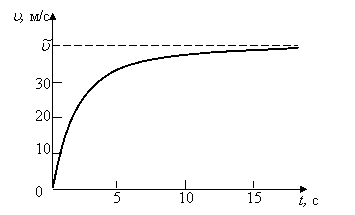
Рис. 2. График зависимости скорости падения от времени
парашютист падение сопротивление математическая модель
При построении математической модели необходимо соблюдение следующих условий:
- манекен массой 50 кг соответственно падают в воздухе с плотностью 1,225 кг/м3;
- на движение влияют только силы линейного и квадратичного сопротивления;
- площадь сечения тела S=0.4 м2;
Тогда для свободно падающего тела под действием сил сопротивления закон Ньютона примет вид:
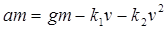 , ,
где a – ускорение тела, м/с2,
m – его масса, кг,
g – ускорение свободного падения на земле, g = 9,8 м/с2,
v – скорость тела, м/c,
k1 – линейный коэффициент пропорциональности, примем k1 = β = 6πμl (μ – динамическая вязкость среды, для воздуха μ = 0,0182 Н.с.м-2; l – эффективная длина, примем для среднестатистического человека при росте 1,7 м и соответствующем обхвате грудной клетки l = 0,4 м),
k2 – квадратичный коэффициент пропорциональности. K2 = α = С2ρS. В данном случае достоверно можно узнать лишь плотность воздуха, а площадь манекена S и коэффициент лобового сопротивления С2 для него определить сложно, можно воспользоваться полученными экспериментальными данными и принять K2 = α = 0,2.
Тогда получим закон Ньютона в дифференциальном виде:
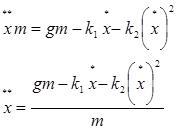
Так как
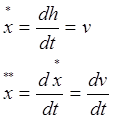
Тогда можно составить систему дифференциальных уравнений:
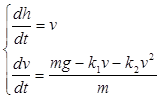
Математическая модель при падении тела в гравитационном поле с учетом сопротивления воздуха выражается системой из двух дифференциальных уравнений первого порядка.
Для имитационного моделирования движения парашютиста в системе MATLAB используем элементы пакета расширения Simulink. Для задания величин начальной высоты - H_n, конечной высоты - H_ k, числа - pi, μ – динамическая вязкость среды - my, обхват - R, массе манекена m, коэффициент лобового сопротивления - c, плотность воздуха - ro, площадь сечения тела - S, ускорение свободного падения - g, начальная скорость - V_n используем элемент Constantнаходящийся в Simulink/Sources(рисунок 3).

Рисунок 3. Элемент
Constant
Для операции умножения используем блок Product, находящийся в Simulink/MathOperations/Product (рисунок 4).

Рисунок. 4
Для ввода k1 – линейного коэффициента пропорциональности и k2 – квадратичного коэффициента пропорциональности используем элемент Gain, находящийся в Simulink/MathOperations/Gain(Рисунок. 5.)

Рисунок. 5
Для интегрирования – элемент Integrator. Находящийсяв Simulink/Continuous/Integrator. Рисунок. 6.

Рисунок. 6
Для вывода информации используем элементы Display и Scope. Находящиеся в Simulink/Sinks. (Рисунок. 7)

Рисунок. 7
Математическая модель для исследования с использованием вышеперечисленных элементов, описывающая последовательный колебательный контур приведена на рисунке 8.

Рисунок. 8
Программа исследований
1. Исследование графика зависимости высоты от времени и скорости от времени масса парашютиста равна 50кг.

Рисунок 9
Из графиков видно, что при расчете падения парашютиста массой 50 кг, следующие данные: максимальная скорость равна 41,6 м/с и время равно 18с , и должна достигаться через 800 м падения, т.е. в нашем случае на высоте около 4200 м.

Рисунок. 10
2. Исследование графика зависимости высоты от времени и скорости от времени масса парашютиста равна 100кг.

Рисунок 11

Рисунок 12
С массой парашютиста 100 кг.: максимальная скорость равна 58 м/с и время равно 15с , и должна достигаться через 500 м падения, т.е. в нашем случае на высоте около 4500 м. (рисунок. 11., рисунок. 12).
Выводы по полученным данным, которые справедливы для манекенов, отличающихся только массой, но с одинаковыми размерами, формой, типом поверхности и другими параметрами, определяющими внешний вид объекта.
Легкий манекен при свободном падении в гравитационном поле с учетом сопротивления среды достигает меньшей предельной скорости, но за меньший промежуток времени и, естественно, при одинаковой начальной высоте – в более низкой точке траектории, чем тяжелый манекен.
Чем тяжелее манекен, тем быстрее он достигнет земли.
4.
Решение задачи программным путем
М-файл функции parashut.m:
%Функция моделирования движения парашютиста
function dhdt=parashut(t,h)
global k1 k2 g m
% система ДУ первого порядка
dhdt(1,1)= -h(2);
dhdt(2,1)=(m*g-k1*h(2)-k2*h(2)*h(2))/m
М-файл вывода результатов parashutist.m:
% Моделирование движения парашютиста
% Васильцов С. В.
clc
global h0 g m k1 k2 a
% k1-линейный коэффициент пропорциональности, определяющийся свойствами среды и формой тела. Формула Стокса.
k1=6*0.0182*0.4;
%k2-квадратичный коэффициент пропорциональности, пропорционален площади сечения тела, поперечного по
%отношения к потоку, плотности среды и зависит от формы тела.
k2=0.5*1.2*0.4*1.225
g=9.81; % ускорение свободного падения
m=50; % масса манекена
h0=5000; % высота
[t h]= ode45(@parashut,[0 200],[h0 0] )
r=find(h(:,1)>=0);
s=length(r);
b=length(t);
h(s+1:b,:)=[];
t(s+1:b,:)=[];
a=g-(k1*-h(:,2)+k2*h(:,2).*h(:,2))/m % вычисляемускорение
% Построение графика зависимости высоты от времени
subplot(3,1,1), plot(t,h(:,1),'LineWidth',1,'Color','r'),grid on;
xlabel('t, c'); ylabel('h(t), m');
title('Графикзависимостивысотыотвремени', 'FontName', 'Arial','Color','r','FontWeight','bold');
legend('m=50 kg')
% Построение графика зависимости скорости от времени
subplot(3,1,2), plot(t,h(:,2),'LineWidth',1,'Color','b'),grid on;
xlabel('t, c');
ylabel('V(t), m/c');
Title('Графикзависимостискоростиотвремени', 'FontName', 'Arial','Color','b','FontWeight','bold');
legend('m=50 kg')
% Построение графика зависимости ускорения от времени
subplot(3,1,3), plot(t,a,'-','LineWidth',1,'Color','g'),grid on;
text (145, 0,'t, c');
ylabel('a(t), m/c^2');
Title('Графикзависимостиускоренияотвремени', 'FontName', 'Arial','Color','g','FontWeight','bold');
legend('m=50 kg')
Экранная форма вывода графиков.
      
Список использованных источников
1. Вся физика. Е.Н. Изергина. – М.: ООО «Издательство «Олимп», 2001. – 496 с.
2. Касаткин И. Л. Репетитор по физике. Механика. Молекулярная физика. Термодинамика/ Под ред. Т. В. Шкиль. – Ростов Н/Д: изд-во «Феникс», 2000. – 896 с.
3. Компакт-диск «Самоучитель MathLAB». ООО «Мультисофт», Россия, 2005.
4. Методические указания к Курсовой работе: дисциплина Математическое моделирование. Движение тела при учете сопротивления среды. – Минск. РИИТ БНТУ. Кафедра ИТ, 2007. – 4 с.
5. Решение систем дифференциальных уравнений в Matlab. Дубанов А.А. [Электронный ресурс]. – Режим доступа: http://rrc.dgu.ru/res/exponenta/ educat/systemat/dubanov/index.asp.htm;
6. Энциклопедия д.д. Физика. Т. 16. Ч.1. с. 394 – 396. Сопротивление движению и силы трения. А. Гордеев. /Глав. ред. В.А. Володин. – М. Аванта+, 2000. – 448 с.
7. MatlabFunctionReference [Электронный ресурс]. – Режим доступа: http://matlab.nsu.ru/Library/Books/Math/MATLAB/help/techdoc/ref/.
|