Введение
Тема контрольной работы «Построение графиков функций. Решение нелинейных уравнений
и систем нелинейных уравнений
» по дисциплине «Информатика».
Цель и задачи работы:
1. Научиться создавать и применять ранжированные переменные.
2. Научиться строить графики в декартовой системе.
3. Научиться решению нелинейных уравнений и систем нелинейных уравнений с помощью решающего блока.
4. Решение системы линейных уравнений матричным способом.
При решении многих технических задач математические модели решения представляют собой нелинейные уравнения, системы нелинейных уравнений, системы линейных уравнений.
Уравнения и системы уравнений, возникающие в практических задачах, обычно можно решить только численно. Методы численного решения реализованы и в программе MathCad.
Для выполнения практической части:
Загрузить
программу MathCADс помощью ярлыка.
Сохранить файл
в собственной папке под именем ….
Задание №1
Создать ранжированные переменные и вывести таблицы их значений
1. Создать ранжированную переменную z
, которая имеет:
начальное значение 1
конечное значение 1.5
шаг изменения переменной 0.1
и вывести таблицу значений переменнойz
2. Создать ранжированную переменную y
, которая имеет:
начальное значение 2
конечное значение 7
шаг изменения переменной 1
и вывести таблицу значений переменной y
3. Создать ранжированную переменную t, которая имеет:
начальное значение a
конечное значение b
шаг изменения переменной h
и вывести таблицу значений переменнойt
Для создания ранжированных переменных используют Палитру
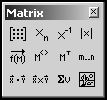
|
Последовательность действий:
1.
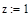 (ввести начальное значение) (ввести начальное значение)
2.
(запятая)
3.
ввести следующее значение (1.1)
4.
нажимают кнопку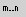
5.
1.5 (ввести конечное значение
|
Если шаг изменения =1, то не выполняют пункты 2. и 3.
Для вывода таблицы значений, достаточно ввести имя переменной и знак  . .
Выполнение Задания №
1
| 1.1 |
1.2 |
1.3 |
 |
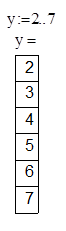 |
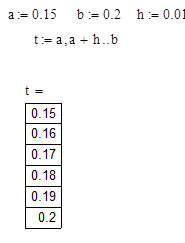 |
Задание ранжированной переменной в виде  удобно
тем, что изменяя значения a, h, bавтоматически изменяется и таблица вывода ранжированной переменной удобно
тем, что изменяя значения a, h, bавтоматически изменяется и таблица вывода ранжированной переменной |
Задание №2
Построить график функции
f
(
x
)=
sin
(
x
)+
ex
-2
на диапазоне [-5; 2
]
Выполнение задания №
2
Последовательность действий:
1. Создать ранжированную переменную x

2. Создать функцию пользователя 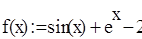
3. Для построения графика использовать Палитру Graph
и кнопку 
|

|
4. Ввести в место ввода по оси X
имя независимого аргумента – x
5. Ввести в место ввода по оси Y
– f
(
x
)
6. Отвести от графика указатель мыши и щелкнуть левой кнопкой мыши. График будет построен
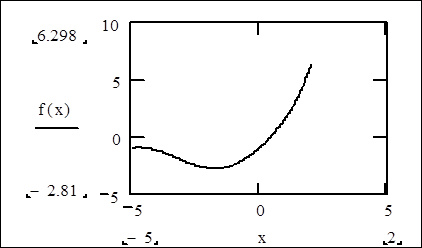
Рис. 1.1
Для форматирования графика, дважды щелкнуть в области графика.
Появится диалоговое окно

|
В этом окне
1.на Вкладке
Ось X
-
Y
установитьпереключатель
Пересечение
2.на Вкладке
Трассировки можно установить цвет и толщину линии
|
Если щелкнуть по графику (появятся маркеры вокруг графика), то методом протягивания в нужном направлении можно изменить размеры графика.
Так выглядит график после форматирования

Рис. 1.2
Теоретическая часть
Блок уравнений и неравенств, требующих решения, записывается после ключевого слова Given (дано
). При записи уравнений используется знак логического равенства =
, кнопка находится в Палитре
Boolean.
Заканчивается блок решения вызовом функции Find(найти
). В качестве аргументов этой функции – искомая
величина. Если их несколько (при решении систем уравнений, то искомые неизвестные должны быть перечислены через запятую).
Всякое уравнение с одним неизвестным может быть записано в виде, f(x)=0,
где f(x) – нелинейная функция. Решение таких уравнений заключается в нахождении корней, т.е. тех значений неизвестного x
, которые обращают уравнение в тождество. Точное решение нелинейного уравнения далеко не всегда возможно. На практике часто нет необходимости в точном решении уравнения. Достаточно найти корни уравнения с заданной степенью точности.
Процесс нахождения приближенных корней уравнения состоит из двух этапов:
1 этап. Отделение корней, т.е. разбиения области определения функции f(x), на отрезки, в каждом из которых содержится только один корень уравнения.
2 этап.Уточнение приближенных корней уравнения, т.е. доведение их до заданной степени точности.
Практическая часть
Задание №1
Постановка задачи:
Найти корень уравнения x
3
-
x
2
=2 с точностью Е=0,00001
Приведем заданное уравнение к виду f
(
x
)
=0
x
3
-
x
2
-2 =0 f
(
x
)
= x
3
-
x
2
-2
Выполнение задания №
1
1 этап – отделение корней
Из графика
видно, что приближенное значение
x
=1.5
(то значение x, при котором функция пересекает ось x)
2 этап – уточнение приближенного значения корня
Специальный вычислительный блок имеет следующую структуру
|
 |
Задают начальное значение x (из графика – приближенное) |
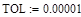 |
TOL– Системная переменная, которой присваивается значение требуемой точности 0.00001 |
Так как требуемая точность вычисления 0.00001, то дважды щелкнув по результату, необходимо отформатировать результат (задать нужное количество десятичных знаков).
| Given |
Given (дано
) – ключевое слово, открывающее
блок решения
|
| x3
-x2
–2 =
0 |
Так записывается уравнение. При записи уравнений в решающем блоке используют знак логического равенства =
, которому соответствует кнопка  Палитры Палитры  |
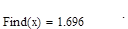 |
Вызвать функции Find, которая в качестве аргументов должна содержать искомую величины (если их несколько, то они перечисляются через запятую) |

Ответ:
x
=1.69562
Проверка
:
Найденное значение корня подставим в заданное уравнение.
Если xнайден верно, то f(x)=0 (так как мы ищем приближенное
значение, то в правой части может быть не нуль, а очень малое значение < Е (требуемой точности)
Уточнение корня в программе MathCad
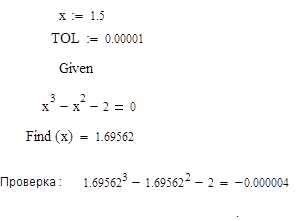
Задание №2
Постановка задачи:
Решить систему уравнений  с точностью Е=0.00001 с точностью Е=0.00001
Выполнение задания №
2

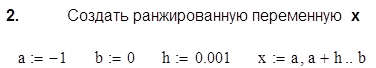
3.
Построить графики функций y1 (x) и y2 (x)

4. Находим из графика точку пересечения кривых

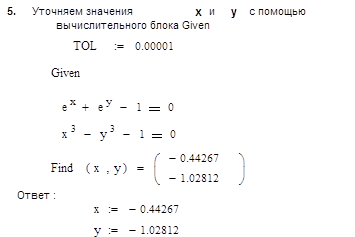
Проверка:
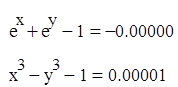
Литература
1. Симонович С. Информатика: базовый курс. – СПб.: Питер, 1999, 640 с.
2. Дьяконов В. MATHCAD 8/2000: специальный справочник – СПБ: Питер, 2001. – 592 с.
|