КУРСОВА РОБОТА
"Властивості лінійних операторів та їх застосування при розв’язанні задач. Матриця лінійного оператора"
Запоріжжя 2010
1.
Поняття лінійного оператора. Алгебраїчні операції над операторами
Нехай  і і  два різних лінійних простору над полем комплексних чисел. Відображення два різних лінійних простору над полем комплексних чисел. Відображення  , яке ставляє у відповідність кожному вектору , яке ставляє у відповідність кожному вектору  простору простору  деякий вектор деякий вектор  простору простору  , будемо називати оператором , будемо називати оператором  , діючий із , діючий із  в в  . Якщо . Якщо  є образом вектора є образом вектора  , то пишуть , то пишуть  . .
Оператор  називається лінійним, якщо виконуються дві умови: називається лінійним, якщо виконуються дві умови:
1.  (властивість адитивності); (властивість адитивності);
2.  (властивість однорідності); (властивість однорідності);
Тут  довільно взяті вектори простору довільно взяті вектори простору  , , 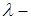 довільно комплексне число. довільно комплексне число.
Позначимо через  множина всіх лінійних операторів, діючих із множина всіх лінійних операторів, діючих із  в в  . Два лінійних оператора . Два лінійних оператора  і і  будемо вважати рівними, якщо для будь – якого вектору будемо вважати рівними, якщо для будь – якого вектору  простору простору 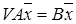 . Визначимо тепер операцію додавання із множини . Визначимо тепер операцію додавання із множини  і операцію множення оператора на число. Під сумою двох лінійних операторів і операцію множення оператора на число. Під сумою двох лінійних операторів  і і  розуміють оператор розуміють оператор  такий, що для будь – якого вектора такий, що для будь – якого вектора  простору простору 
 . .
Під добутком лінійного оператора  на комплексне число на комплексне число  розуміють оператор розуміють оператор  такий, що для любого вектора такий, що для любого вектора  простору простору 
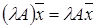
Неважко переконатися в тому, що оператори  і і  лінійні. лінійні.
Оператор 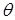 називається нульовим, якщо для будь – якого вектору називається нульовим, якщо для будь – якого вектору  простору простору   . .
Щоб переконатися, що оператор 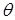 лінійний і, як наслідок, належності множині лінійний і, як наслідок, належності множині  , потрібно показати, що для довільно взятих векторів , потрібно показати, що для довільно взятих векторів  простору простору  мають місце рівності мають місце рівності  і і  . Так як будь – якому вектору простору . Так як будь – якому вектору простору  оператор оператор 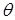 ставить у відповідність вектор ставить у відповідність вектор  , то , то   . Як наслідок, . Як наслідок, 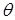 - лінійний оператор. - лінійний оператор.
Введемо поняття оператора, протилежному лінійному оператору  . Оператор – . Оператор –  називається протилежним оператором називається протилежним оператором  , якщо , якщо  . Неважко перевірити, що для довільно взятого оператору . Неважко перевірити, що для довільно взятого оператору  із із 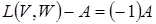 і що і що  лінійний оператор. лінійний оператор.
Введені на множині  лінійні операції над її елементами (операторами) мають такі властивості: лінійні операції над її елементами (операторами) мають такі властивості:
1. , ,
2.  , ,
3. існує один лінійний оператор  такий, що для будь – якого лінійного оператора такий, що для будь – якого лінійного оператора  із із  
4. для кожного оператора 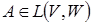 існує єдиний оператор – існує єдиний оператор –  такий, що такий, що  . .
Із перелічених властивостей лінійних операцій над елементами множини  випливає, що множина випливає, що множина  по відношенню до операції суми операторів є адитивною абелевою групою. Операція множення на число має такі властивості по відношенню до операції суми операторів є адитивною абелевою групою. Операція множення на число має такі властивості   . .
Всі перелічені властивості лінійних операцій над елементами множини  дозволяє стверджувати, що множина дозволяє стверджувати, що множина  є лінійним простором над полем комплексних чисел. Звідси випливає, що можна ставити питання про розмірність цього простору, про його базиси, підпросторів. є лінійним простором над полем комплексних чисел. Звідси випливає, що можна ставити питання про розмірність цього простору, про його базиси, підпросторів.
2.
Лінійні перетворення (оператори) із простору V в V
В подальшому будемо розглядати лінійні оператори, діючі із лінійного простору  в той самий простір. Ці оператори називають також перетвореннями із в той самий простір. Ці оператори називають також перетвореннями із  в в  . .
Назвемо тотожнім (одиничним) оператор  такий, що для любого вектора такий, що для любого вектора  простору простору  . Очевидно, . Очевидно,  , , 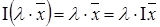 , для любих , для любих 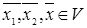 . З цього випливає, оператор . З цього випливає, оператор  – лінійний і, тому, – лінійний і, тому,  . Неважко упевнитися в тому, що оператор . Неважко упевнитися в тому, що оператор  – єдиний. Дійсно, якщо припустити що, крім тотожного оператора – єдиний. Дійсно, якщо припустити що, крім тотожного оператора  з з  , існує ще один тотожний оператор , існує ще один тотожний оператор  , тоді для будь-якого , тоді для будь-якого  будемо мати будемо мати  , ,  , очевидно, , очевидно, 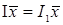 , тобто , тобто  . .
Введемо операцію множення операторів. Нехай  та та  – два будь-яких лінійних оператора з – два будь-яких лінійних оператора з  , а , а  – довільний вектор простору – довільний вектор простору  . Очевидно вектор . Очевидно вектор 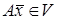 , тому цей вектор можна привести за допомогою оператора , тому цей вектор можна привести за допомогою оператора  . В результаті вектор . В результаті вектор  буде перетворений до вектору буде перетворений до вектору  . Оператор, який приводить довільний вектор . Оператор, який приводить довільний вектор  простору простору  у вектор у вектор  , називається добутком операторів , називається добутком операторів  та та  і позначається так: і позначається так:  . За означенням добутку операторів . За означенням добутку операторів  і і   для будь-якого вектору для будь-якого вектору  . Легко перевірити, що . Легко перевірити, що   , ,  , де , де  – довільно вибране комплексне число. З цього слідує, що добуток лінійних операторів є лінійним оператором, тобто – довільно вибране комплексне число. З цього слідує, що добуток лінійних операторів є лінійним оператором, тобто  . Зауважимо, що . Зауважимо, що  . .
Операції додавання та множення лінійних операторів мають наступні властивості
1)  , 3) , 3)  , ,
2)  , 4) , 4)  . .
Для ілюстрації способу доведення цих властивостей доведемо властивість  . Нехай . Нехай  – довільний вектор простору – довільний вектор простору  . Для довільного вектору . Для довільного вектору  простору простору  за означенням добутку і суми операторів має за означенням добутку і суми операторів має

Таким чином,  , тобто , тобто  . .
Якщо для оператору  можна вказати такий лінійний оператор можна вказати такий лінійний оператор  , що , що  , то оператор , то оператор  називають оберненим для оператору називають оберненим для оператору  . Можна показати, що оператор . Можна показати, що оператор  – єдиний. – єдиний.
Покажемо, що оператор  , що має обернений, перетворює ненульовий вектор в ненульовий, тобто якщо , що має обернений, перетворює ненульовий вектор в ненульовий, тобто якщо  , то й , то й  . Спочатку доведемо, що . Спочатку доведемо, що 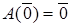 . Дійсно, так як . Дійсно, так як  – лінійний оператор, то для будь-якого – лінійний оператор, то для будь-якого  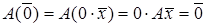 . Доведене твердження справедливе для будь-якого лінійного оператора, в тому числі і для оператора, що має обернений, і для оператора . Доведене твердження справедливе для будь-якого лінійного оператора, в тому числі і для оператора, що має обернений, і для оператора  . Нехай . Нехай  і і  . Так як оператор . Так як оператор  має обернений, то має обернений, то 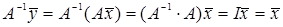 , тобто , тобто  . Якщо припустити, що деякому . Якщо припустити, що деякому  відповідає вектор відповідає вектор  , тоді на основі установлених рівностей , тоді на основі установлених рівностей  і і  виходило б, що виходило б, що  . А це заперечує початковому фактові, що . А це заперечує початковому фактові, що  . З цього випливає, що припущення про те, що для деякого . З цього випливає, що припущення про те, що для деякого   , невірно, тому для будь – якого , невірно, тому для будь – якого   . .
Доведемо ще одну властивість оператора  , що має обернений. Такий оператор два різних вектора , що має обернений. Такий оператор два різних вектора 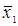 та та  перетворює у два різні вектори перетворює у два різні вектори  і і  . Дійсно, якщо припустити противне, що існують такі нерівні один одному . Дійсно, якщо припустити противне, що існують такі нерівні один одному 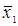 і і  , для яких , для яких 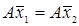 , тоді для таких , тоді для таких 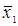 і і  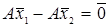 або, що те саме або, що те саме  . За умовою оператор . За умовою оператор  має обернений. За доведеною вище властивістю такого оператора із рівності має обернений. За доведеною вище властивістю такого оператора із рівності  випливає, що випливає, що 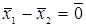 , тобто , тобто  . Ми прийшли до протиріччя з тим фактом, що за умовою . Ми прийшли до протиріччя з тим фактом, що за умовою  . З цього випливає, що будь – яким двом різним векторам . З цього випливає, що будь – яким двом різним векторам 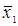 і і  відповідають різні образи відповідають різні образи  і і  . .
Оператор  називають взаємно – однозначним, якщо два будь – які різні вектори називають взаємно – однозначним, якщо два будь – які різні вектори 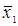 і і  він перетворює у різні вектори він перетворює у різні вектори  і і  . Із наведеного вище випливає, що оператор . Із наведеного вище випливає, що оператор  , що має обернений, є взаємно – однозначним. Для взаємно – однозначного оператора неважко довести таку властивість: якщо , що має обернений, є взаємно – однозначним. Для взаємно – однозначного оператора неважко довести таку властивість: якщо  , то і , то і  . Покажемо, що взаємно – однозначний оператор . Покажемо, що взаємно – однозначний оператор  лінійно незалежні вектори лінійно незалежні вектори 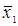 , ,  , …, , …,  перетворює в лінійно незалежні вектори перетворює в лінійно незалежні вектори  , ,  , …, , …,  . Для доведення цього твердження скористаємося методом «від противного». Припустимо противне, що вектори . Для доведення цього твердження скористаємося методом «від противного». Припустимо противне, що вектори  , …, , …,  – лінійно незалежні. Тоді можна знайти такі не рівню нулю числа, – лінійно незалежні. Тоді можна знайти такі не рівню нулю числа,  що що  . Так як оператор . Так як оператор  – лінійний, то – лінійний, то  . .
Звідси за властивістю взаємно-однозначного оператора  , тобто вектори , тобто вектори 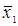 , ,  , …, , …,  виявляються лінійно залежними. Протиріччя з умовою ствердження означає, що вектори виявляються лінійно залежними. Протиріччя з умовою ствердження означає, що вектори  , ,  , …, , …,  лінійно незалежні. лінійно незалежні.
Із доведеного випливає, що будь-який вектор  простору простору  має єдиний прообраз має єдиний прообраз  такий, що такий, що  . Доведемо тільки єдність прообразу вектора . Доведемо тільки єдність прообразу вектора  . Дійсно, якщо припустити, що вектор . Дійсно, якщо припустити, що вектор  має декілька різноманітних прообразів, наприклад, має декілька різноманітних прообразів, наприклад, 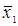 і і  , то виявиться, що , то виявиться, що  . Звідси . Звідси  , маємо , маємо  , так як оператор взаємно-однозначний. Отже, якщо оператор , так як оператор взаємно-однозначний. Отже, якщо оператор  – взаємно-однозначний, то кожному вектору – взаємно-однозначний, то кожному вектору  простору простору  він ставить у відповідність один і тільки один вектор він ставить у відповідність один і тільки один вектор  . Звідси випливає, що взаємно-однозначний оператор має обернений. . Звідси випливає, що взаємно-однозначний оператор має обернений.
Підводячи підсумок сказаному вище про властивості оберненого і взаємно-однозначного операторів, сформулюємо наступне твердження.
Теорема 2.1. Для того, щоб лінійний оператор  мав обернений необхідно і достатньо, щоб він був взаємно-однозначним. мав обернений необхідно і достатньо, щоб він був взаємно-однозначним.
Введемо поняття ядра й образу оператора. Ядром лінійного оператора  називають таку множину називають таку множину  векторів простору векторів простору  , що для любого , що для любого   . Відомо, що будь-який лінійний оператор приводить вектор . Відомо, що будь-який лінійний оператор приводить вектор 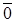 в в 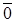 , тобто , тобто  , тому ядро довільного лінійного оператора не є пустою множиною, так як воно завжди містить оператор , тому ядро довільного лінійного оператора не є пустою множиною, так як воно завжди містить оператор 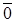 . .
Теорема 2.2. Якщо  містить єдиний вектор містить єдиний вектор 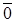 , то оператор , то оператор  є взаємно-однозначним. є взаємно-однозначним.
Доведення. Нехай  - два довільно взятих вектора лінійного простору. Якщо показати, що - два довільно взятих вектора лінійного простору. Якщо показати, що 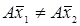 , то це буде означати, що оператор , то це буде означати, що оператор  є взаємно-однозначним. Припустимо противне, що знайдуться два вектора є взаємно-однозначним. Припустимо противне, що знайдуться два вектора 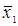 і і  , такі, що , такі, що  , а , а  . Тоді для цих векторів . Тоді для цих векторів  . За умовою теореми . За умовою теореми  складається із єдиного вектора складається із єдиного вектора 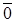 , тобто для вектора , тобто для вектора 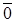 і тільки для нього і тільки для нього  . В силу цього . В силу цього  чи чи  . Ми прийшли до протиріччя з припущенням про те, що . Ми прийшли до протиріччя з припущенням про те, що  . Тому для будь-яких не рівних один одному векторів . Тому для будь-яких не рівних один одному векторів 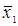 і і  простору простору   . Отже, твердження теореми вірне. . Отже, твердження теореми вірне.
Теорема 2.3. Для того, щоб оператор  мав обернений, необхідно і достатньо, щоб мав обернений, необхідно і достатньо, щоб  . .
Доведення цієї теореми основується на теоремах 2.1 і 2.2 про обернений оператор і ядро взаємно-однозначного оператора.
Образом оператора  називається множина називається множина  всіх векторів простору всіх векторів простору  , кожний з яких має прообраз, тобто якщо , кожний з яких має прообраз, тобто якщо  , то існує такий вектор , то існує такий вектор 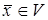 , що , що  . Легко побачити, що якщо . Легко побачити, що якщо  містить тільки нульовий вектор, то містить тільки нульовий вектор, то  є весь лінійний простір є весь лінійний простір  : :  . Дійсно, якщо . Дійсно, якщо  , то оператор , то оператор  є взаємно-однозначним. За доведеною вище властивістю взаємно-однозначного оператора кожний вектор є взаємно-однозначним. За доведеною вище властивістю взаємно-однозначного оператора кожний вектор  простору простору  має єдиний прообраз має єдиний прообраз  : :  , так що , так що  . .
Покажемо тепер, що множина  для довільного лінійного простору для довільного лінійного простору  є підпростором лінійного простору є підпростором лінійного простору  . Нехай . Нехай 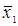 і і  – два довільно взятих вектори множини – два довільно взятих вектори множини  . Так як . Так як  , то , то  . Нехай . Нехай  – довільне число. Так як – довільне число. Так як  , то , то 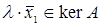 . Таким чином, лінійні операції над будь-якими векторами множини . Таким чином, лінійні операції над будь-якими векторами множини  дають вектори тієї ж множини, тобто дають вектори тієї ж множини, тобто  – підпростір простору – підпростір простору  . .
Аналогічним способом доводиться, що множина  також є підпростором простору також є підпростором простору  . .
Розмірність підпростору  називається дефектом оператора називається дефектом оператора . Розмірність підпростору . Розмірність підпростору  називається рангом оператора називається рангом оператора  . Для рангу оператора . Для рангу оператора  використовується одне з позначень використовується одне з позначень  або або  , для позначення дефекту оператора використовується символ , для позначення дефекту оператора використовується символ  . .
Теорема 2.4. Для будь-якого лінійного оператора  із із  сума розмінностей його ядра і образу дорівнює розмірності простору сума розмінностей його ядра і образу дорівнює розмірності простору  , тобто , тобто 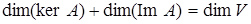 або або  . .
Теорема 2.5. Нехай 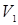 і і  - два яких-небудь підпростори - два яких-небудь підпростори  - мірного простору - мірного простору  , причому , причому  . Тоді існує такий лінійний оператор . Тоді існує такий лінійний оператор  , що , що  , а , а 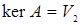 . .
Доведення. Нехай  - розмірність підпростору - розмірність підпростору 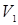 , тобто , тобто  , а , а 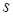 – розмірність підпростору – розмірність підпростору  . За умовою теореми . За умовою теореми  . Виберемо базис . Виберемо базис   - мірного простору - мірного простору  так, щоб так, щоб 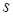 векторів векторів  було базисом підпростору було базисом підпростору  . В підпросторі . В підпросторі 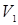 візьмемо який-небудь базис візьмемо який-небудь базис  . Розглянемо лінійний оператор . Розглянемо лінійний оператор  , який перетворює вектори , який перетворює вектори  простору простору  у вектори у вектори  , а кожний з векторів , а кожний з векторів  у нульовий вектор, тобто у нульовий вектор, тобто  . .
Оператор  довільний вектор довільний вектор 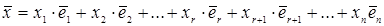 простору простору  приводить у вектор приводить у вектор   , який належить підпростору , який належить підпростору 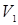 простора простора  . Звідси випливає, що . Звідси випливає, що  , тобто підпростір , тобто підпростір 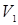 містить образ оператора містить образ оператора  . Щоб довести, що . Щоб довести, що  , треба за означенням множини , треба за означенням множини  показати, що будь-який вектор показати, що будь-який вектор  підпростору підпростору 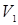 , має прообраз у просторі , має прообраз у просторі  . Розглянутий лінійний оператор . Розглянутий лінійний оператор  перетворює вектори перетворює вектори  простору простору  у вектори у вектори  , тому довільно взятий вектор , тому довільно взятий вектор  підпростору підпростору 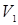 можна представити у вигляді можна представити у вигляді  . В силу лінійності оператора и також того, що . В силу лінійності оператора и також того, що  , вектор , вектор  можна представити також і в такій формі: можна представити також і в такій формі:   , де , де  – довільно вибрані комплексні числа. Останній вираз для довільного вектору – довільно вибрані комплексні числа. Останній вираз для довільного вектору  означає, що він є образом вектора означає, що він є образом вектора  простору простору  . Таким чином, . Таким чином,  . .
Покажемо тепер, що підпростір  є ядром оператора є ядром оператора  . Нехай . Нехай  який-небудь вектор підпростору який-небудь вектор підпростору  . Так як . Так як  , то це означає, що вектор , то це означає, що вектор  входить в ядро оператора входить в ядро оператора  . Звідси випливає, що підпростір . Звідси випливає, що підпростір  . Для доведення того, що . Для доведення того, що 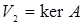 треба показати, що будь-який вектор треба показати, що будь-який вектор  простору простору  , що не належить підпростору , що не належить підпростору  , не може бути елементом ядра оператора , не може бути елементом ядра оператора  . Нехай . Нехай  - вектор простору - вектор простору  , який не належить підпростору , який не належить підпростору  . Зрозуміло, що хоча б одна із координат . Зрозуміло, що хоча б одна із координат  цього вектору не рівна нулю, так як в протилежному випадку цього вектору не рівна нулю, так як в протилежному випадку  . Розглянемо . Розглянемо 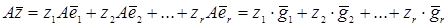 . Так як . Так як  лінійно незалежні вектори, а серед чисел лінійно незалежні вектори, а серед чисел  є відмінні від нуля, то є відмінні від нуля, то 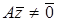 . Це означає, що будь-який вектор, що не належить підпростору . Це означає, що будь-який вектор, що не належить підпростору  , не належить і ядру оператора , не належить і ядру оператора  . Отже, . Отже, 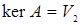 . .
Теорема 2.6. Нехай  і і  – два яких-небудь лінійних оператора із множини – два яких-небудь лінійних оператора із множини  , тоді , тоді  , ,  . .
Доведення. Нехай 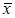 – довільний вектор простору – довільний вектор простору  . Зрозуміло, що . Зрозуміло, що  . Будь-який вектор . Будь-який вектор  множини множини  за означенням добутку операторів це вектор за означенням добутку операторів це вектор  . Останній є вектором множини . Останній є вектором множини  . З цього слідує, що має місце включення . З цього слідує, що має місце включення  . А це означає, що . А це означає, що  , тобто , тобто  . Перше твердження теореми доведено. . Перше твердження теореми доведено.
Доведемо справедливість другого. Нехай 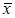 – довільний вектор ядра оператора – довільний вектор ядра оператора  , тоді , тоді 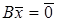 , і, тому, , і, тому,  . Це означає, що якщо . Це означає, що якщо  , то , то  , тобто , тобто  . Звідси випливає нерівність . Звідси випливає нерівність  . Позначимо через . Позначимо через  розмірність простору розмірність простору  . Згідно теореми 2.4 . Згідно теореми 2.4 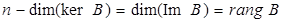 , ,  . Так як . Так як  , то , то  , тобто , тобто  . .
Теорема 2.7. Нехай  – розмірність простору – розмірність простору  , ,  і і  – лінійні оператори із – лінійні оператори із  , тоді , тоді  . .
3.
Матриця лінійного оператора
Нехай  - деякий базис лінійного простору - деякий базис лінійного простору  , а , а  – який-небудь лінійний оператор, діючий із – який-небудь лінійний оператор, діючий із  в в  . Вектор . Вектор  оператор оператор  перетворює в вектор перетворює в вектор  . Вектори . Вектори  простору простору  розкладемо по векторах базису розкладемо по векторах базису  цього простору. Побудуємо матрицю цього простору. Побудуємо матрицю  порядку порядку  , стовпці якої складені із координат векторів , стовпці якої складені із координат векторів  , ,
 , ,  , , 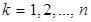 . .
Матриця  називається матрицею оператора називається матрицею оператора  в базисі в базисі  . .
Приклад. Записати матрицю тотожного і нульового операторів у базисі  простору простору  . .
Розв’язок. Тотожний оператор  будь-який вектор простору будь-який вектор простору  приводить в той же самий оператор. Тому приводить в той же самий оператор. Тому  . А це означає, що матриця . А це означає, що матриця  тотожного оператора буде одиничною в будь-якому базисі простору тотожного оператора буде одиничною в будь-якому базисі простору  . Нульовий оператор . Нульовий оператор 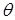 будь-який вектор простору будь-який вектор простору  перетворює в нульовий вектор, тому матриця перетворює в нульовий вектор, тому матриця  цього оператора – нульова в будь-якому базисі. цього оператора – нульова в будь-якому базисі.
Із сказаного вище випливає, що в обраному базисі  -мірного простору -мірного простору  з кожним лінійним оператором з кожним лінійним оператором  можна зв’язати квадратну матрицю можна зв’язати квадратну матрицю  порядку порядку  . Виникає питання: чи можна кожній квадратній матриці . Виникає питання: чи можна кожній квадратній матриці  порядку порядку  поставити у відповідність такий лінійний оператор поставити у відповідність такий лінійний оператор  , матриця якого в заданому базисі , матриця якого в заданому базисі  простору простору  співпадає з матрицею співпадає з матрицею  ? Стверджувальну відповідь на це питання дає ? Стверджувальну відповідь на це питання дає
Теорема 3.1. Нехай  – деяка квадратна матриця порядку – деяка квадратна матриця порядку  . Нехай . Нехай  – довільний обраний базис – довільний обраний базис  -мірного лінійного простору -мірного лінійного простору  . Тоді існує єдиний лінійний оператор . Тоді існує єдиний лінійний оператор  , який у вказаному базисі має матрицю , який у вказаному базисі має матрицю  . .
Доведення. Розглянемо лінійний оператор  , який вектори , який вектори  базису простору базису простору  перетворює у вектори перетворює у вектори 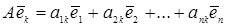 , ,  . У базисі . У базисі  оператор оператор  , очевидно, має матрицю , очевидно, має матрицю  . Залишається довести, що є єдиним оператором з матрицею. Припустимо протилежне, що, крім оператора . Залишається довести, що є єдиним оператором з матрицею. Припустимо протилежне, що, крім оператора  , існує ще лінійний оператор , існує ще лінійний оператор  , маючий матрицю , маючий матрицю  в базисі в базисі  . Це означає, що . Це означає, що  , ,  . Виберемо який-небудь вектор . Виберемо який-небудь вектор  простору простору  і розглянемо вектори і розглянемо вектори  і і  . Маємо . Маємо   . .
Як наслідок, що для будь-якого   . Звідси витікає, що . Звідси витікає, що 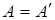 . Теорему доведено. . Теорему доведено.
Теорема 3.2. Нехай  – матриця лінійного оператора – матриця лінійного оператора  в базисі в базисі  простору простору  . Ранг оператора . Ранг оператора  дорівнює рангу його матриці: дорівнює рангу його матриці: 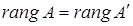 . .
Доведення. В основі доведення лежать означення рангу оператора і рангу матриці:  , ранг матриці , ранг матриці  дорівнює рангу системи його стовпців. дорівнює рангу системи його стовпців.
Нехай  – який-небудь вектор – який-небудь вектор  - мірного простору - мірного простору  . Образом вектора . Образом вектора  є вектор є вектор   . Як бачимо, довільний вектор образу оператора . Як бачимо, довільний вектор образу оператора  , тобто множини , тобто множини  , представляє собою лінійну комбінацію векторів , представляє собою лінійну комбінацію векторів  . Отже, . Отже,  є лінійною оболонкою множини векторів є лінійною оболонкою множини векторів  . Відомо, що розмірність лінійної оболонки дорівнює рангові системи векторів, які вони утворюють, тому . Відомо, що розмірність лінійної оболонки дорівнює рангові системи векторів, які вони утворюють, тому  . За означенням у стовпцях матриці . За означенням у стовпцях матриці  оператора оператора  розміщені координати векторів розміщені координати векторів  у базисі у базисі  . Отже, на основі означення рангу матриці . Отже, на основі означення рангу матриці  . Таким чином, . Таким чином,  . .
Нехай  і і  матриці операторів матриці операторів  і і  в якому-небудь базисі простору в якому-небудь базисі простору  , тоді із способу побудови цих матриць витікає, що матриці операторів , тоді із способу побудови цих матриць витікає, що матриці операторів  і і  , де , де  і і  – довільно взяті числа, рівні відповідно – довільно взяті числа, рівні відповідно  і і 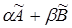 . Доведемо справедливість першого твердження, як більш складного. Дійсно, стовпці матриці оператора . Доведемо справедливість першого твердження, як більш складного. Дійсно, стовпці матриці оператора  побудовані із координат векторів побудовані із координат векторів 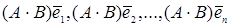 у базисі у базисі  простору простору  . Визначимо елементи . Визначимо елементи  -го стовпця цієї матриці, тобто координати вектора -го стовпця цієї матриці, тобто координати вектора 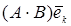 . Маємо . Маємо

Звідси видно, що довільний елемент  матриці матриці  оператора оператора  дорівнює дорівнює  , тобто дорівнює сумі добутків елементів , тобто дорівнює сумі добутків елементів  -го рядка матриці -го рядка матриці  на відповідний елемент на відповідний елемент  -го стовпця матриці -го стовпця матриці  . А це означає, що . А це означає, що  . Твердження доведено. . Твердження доведено.
Із доведеного твердження і теорем 2.6, 2.7 про ранг оператора  слідує справедливість таких нерівностей для двох добутків квадратних матриць слідує справедливість таких нерівностей для двох добутків квадратних матриць  і і  одного порядку одного порядку  . .
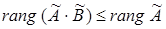 , ,  , ,

Відомо, що необхідною і достатньою умовою існування оберненого оператора для оператора  , є умова , є умова  , де , де  – розмірність простору – розмірність простору  . Із теореми 3.2 витікає, що остання умова еквівалентна вимозі: матриця . Із теореми 3.2 витікає, що остання умова еквівалентна вимозі: матриця  оператора оператора  повинна бути не виродженою. повинна бути не виродженою.
Іншими словами, щоб оператор  мав обернений необхідно і достатньо, щоб його матриця в якому-небудь базисі лінійного простору мав обернений необхідно і достатньо, щоб його матриця в якому-небудь базисі лінійного простору  виявилась не виродженою. виявилась не виродженою.
4.
Перетворення матриці оператора при заміні базису
Нехай у просторі  обрані два базиси обрані два базиси  і і 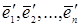 . Перший базис для зручності назвемо старим, а другий – новим. Координати векторів . Перший базис для зручності назвемо старим, а другий – новим. Координати векторів  у старому базисі розмістимо у стовпцях матриці у старому базисі розмістимо у стовпцях матриці
 . .
Побудована матриця називається матрицею переходу від старого базису до нового. Вектори  лінійно незалежні, тому лінійно незалежні, тому  і, звісно, матриця і, звісно, матриця  не вироджена. не вироджена.
Згідно сказаному
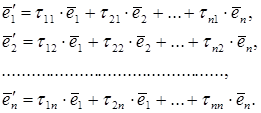  (4.1) (4.1)
Ці формули зв’язку між векторами старого і нового базисів у матричному записі мають вигляд
 , ,
де  – транспонована матриця – транспонована матриця  . .
Теорема 4.1. Матриці  і і  оператора оператора  в базисах в базисах  і і  зв’язані співвідношеннями зв’язані співвідношеннями
 , ,
 , ,
де  – матриця переходу від старого базису – матриця переходу від старого базису  до нового до нового  . .
Доведення. За означенням матриці оператора
 , ,

де  і і  – елементи матриць – елементи матриць  і і  . Замінимо в останній рівності вектори . Замінимо в останній рівності вектори  згідно формулам (4.1), отримаємо згідно формулам (4.1), отримаємо
 (4.2) (4.2)
З іншого боку
 
Але
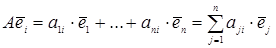
Тому
 (4.3) (4.3)
Із двох отриманих виразів (4.2) і (4.3) для вектора виходить, що
  
У цій рівності вектори  лінійно незалежні, тому коефіцієнти про однакових векторах у лівій і правій частинах рівності мають бути однаковими, отже, лінійно незалежні, тому коефіцієнти про однакових векторах у лівій і правій частинах рівності мають бути однаковими, отже,
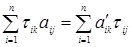 , , 
Згідно означенню добутку двох матриць звідси витікає матричне рівність 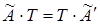 . Якщо помножити обидві частини цієї рівності на . Якщо помножити обидві частини цієї рівності на  праворуч, то отримаємо праворуч, то отримаємо  , якщо помножити на , якщо помножити на 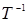 злів, то будемо мати злів, то будемо мати  . Теорему доведено. . Теорему доведено.
Матриці  і і  одного й того ж порядку називаються подібними, якщо можна знайти таку не вироджену матрицю одного й того ж порядку називаються подібними, якщо можна знайти таку не вироджену матрицю 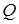 того ж порядку, що того ж порядку, що 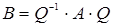 . Із цього означення і теореми 4.1 витікає, що матриці оператора . Із цього означення і теореми 4.1 витікає, що матриці оператора  у різних базисах виявляються побідними. Покажемо, що визначники подібних матриць у різних базисах виявляються побідними. Покажемо, що визначники подібних матриць  і і  рівні. Дійсно, згадавши, що визначник добутку квадратних матриць дорівнює добутку визначників співмножників, можемо записати рівні. Дійсно, згадавши, що визначник добутку квадратних матриць дорівнює добутку визначників співмножників, можемо записати
 . .
Із доведеного твердження виходить, що визначник матриці оператора не змінюється при заміні базису. У зв’язку з цим доречно ввести поняття визначника оператора. Визначником оператора  називають число називають число  , рівне визначнику матриці оператора , рівне визначнику матриці оператора  в якому-небудь базисі простору. в якому-небудь базисі простору.
Приклад. Лінійний оператор  діє на вектори базису діє на вектори базису  наступним чином: наступним чином: 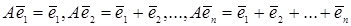 . Знайти визначник оператора . Знайти визначник оператора  . .
Розв’язок. Матриця оператора  у базисі у базисі  має вигляд має вигляд
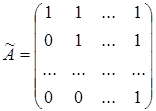 , ,
тобто є верхньою трикутною. Визначник цієї матриці дорівнює одиниці, тому і 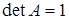 . .
5.
Власні значення і власні вектори оператора
Число  називається власним числом лінійного оператора називається власним числом лінійного оператора  , якщо у просторі , якщо у просторі  можна знайти такий ненульовий вектор можна знайти такий ненульовий вектор  , що , що
 (5.1) (5.1)
Будь-який ненульовий вектор, задовольняючий рівності (5.1), називають власним вектором оператора  , що відповідає власному значенню , що відповідає власному значенню  . .
Рівність (5.1) можна записати по іншому 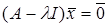 , де , де  – тотожний оператор. Оскільки – тотожний оператор. Оскільки  – ненульовий вектор, то зрозуміло, що розмірність ядра оператора – ненульовий вектор, то зрозуміло, що розмірність ядра оператора  не менше одиниці. Нехай не менше одиниці. Нехай  – розмірність простору – розмірність простору  , в якому діє оператор , в якому діє оператор  . Відомо, що . Відомо, що  . Звісно, . Звісно,
 . Але тоді . Але тоді 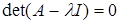 . .
Таким чином, якщо число  є власним значенням оператора є власним значенням оператора  , то , то  є коренем рівняння є коренем рівняння 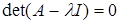 (характеристичне рівняння або вікове рівняння оператора (характеристичне рівняння або вікове рівняння оператора  ). ).
Вияснимо, чи всі корені характеристичного рівняння 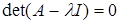 будуть власними значеннями оператора будуть власними значеннями оператора  . Нехай . Нехай 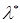 – який-небудь корінь рівняння, тоді для цього значення – який-небудь корінь рівняння, тоді для цього значення   . Це означає, що матриця оператора . Це означає, що матриця оператора  буде виродженою у будь-якому базисі простору буде виродженою у будь-якому базисі простору 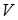 . Як наслідок, . Як наслідок,  . Так як . Так як 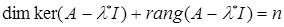 , то , то  . А це означає, що існую по меншій мірі один ненульовий вектор . А це означає, що існую по меншій мірі один ненульовий вектор  , такий, що , такий, що 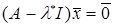 чи чи  . Таким чином, будь-який корінь характеристичного рівняння . Таким чином, будь-який корінь характеристичного рівняння 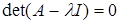 буде власним значенням оператора буде власним значенням оператора  , тобто вірне твердження. , тобто вірне твердження.
Теорема 5.1. Для того, щоб комплексне число  було власним значенням лінійного оператора було власним значенням лінійного оператора  , необхідно і достатньо, щоб це число було коренем характеристичного рівняння , необхідно і достатньо, щоб це число було коренем характеристичного рівняння 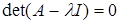 . .
Нехай  – базис простору – базис простору 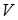 и нехай и нехай
 , ,
матриця лінійного оператора  у цьому базисі. Відомо, що матриця тотожного оператора у цьому базисі. Відомо, що матриця тотожного оператора  в будь-якому базисі буде одиничною, тому в розглянутому базисі простору в будь-якому базисі буде одиничною, тому в розглянутому базисі простору 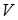 оператор оператор 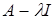 характеризується такою матрицею характеризується такою матрицею
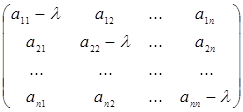 . .
Визначник цієї матриці, тобто  , називається характеристичним або віковим визначником оператора , називається характеристичним або віковим визначником оператора  . Легко побачити, що добуток елементів . Легко побачити, що добуток елементів 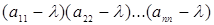 головної діагоналі вікового визначника буде многочленом степені головної діагоналі вікового визначника буде многочленом степені  , решта членів визначника будуть многочленами степені не вище , решта членів визначника будуть многочленами степені не вище 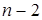 . З цього видно, що віковий визначник оператора . З цього видно, що віковий визначник оператора  є многочленом степені є многочленом степені  . За наслідком з основної теореми алгебри такий многочлен має . За наслідком з основної теореми алгебри такий многочлен має  коренів, якщо кожний корінь рахувати стільки разів, яка його кратність. Тому число власних значень оператора коренів, якщо кожний корінь рахувати стільки разів, яка його кратність. Тому число власних значень оператора  , діючого в , діючого в  -мірному просторі, дорівнює -мірному просторі, дорівнює  , якщо кожне власне значення рахувати стільки разів, яка його кратність. , якщо кожне власне значення рахувати стільки разів, яка його кратність.
Відомо, що в різних базисах простору 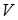 матриці оператора матриці оператора  , взагалі-то, різні. У зв’язку з цим виникає питання про пошук такого базису простору , взагалі-то, різні. У зв’язку з цим виникає питання про пошук такого базису простору 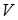 , в якому матриця оператора має найпростіший вигляд (найбільше число нульових елементів). Припустімо, що у просторі , в якому матриця оператора має найпростіший вигляд (найбільше число нульових елементів). Припустімо, що у просторі 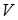 існує базис існує базис  всі вектори якого є власними векторами оператора всі вектори якого є власними векторами оператора  , тобто , тобто   . У цьому базисі матриця оператора буде мати діагональний вигляд . У цьому базисі матриця оператора буде мати діагональний вигляд
 . .
Навпаки, якщо в якому-небудь базисі простору 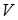 матриця лінійного оператора матриця лінійного оператора  має діагональний вид, то всі вектори базису є власними векторами оператора має діагональний вид, то всі вектори базису є власними векторами оператора  . Таким чином, доведено наступне твердження. . Таким чином, доведено наступне твердження.
Теорема 5.2. Для того, щоб матриця лінійного оператора  у базисі у базисі  простору простору 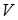 була діагональною, необхідно і достатньо, щоб вектори була діагональною, необхідно і достатньо, щоб вектори  були власними векторами оператора були власними векторами оператора  . Теорема 5.3. Якщо власні значення . Теорема 5.3. Якщо власні значення 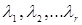 лінійного оператора лінійного оператора  , діючого в , діючого в  -мірному просторі -мірному просторі 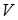 , різні, тоді відповідні їм власні вектори , різні, тоді відповідні їм власні вектори  лінійно незалежні. лінійно незалежні.
Наслідок. Якщо характеристичне рівняння 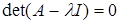 має має  різних коренів, то у різних коренів, то у  -мірному векторному просторі існує базис, в якому матриця оператора -мірному векторному просторі існує базис, в якому матриця оператора  має діагональний вид. має діагональний вид.
Якщо оператор  має кратні власні значення, то може виявитися, що максимальна лінійно незалежна сукупність власних векторів оператора має кратні власні значення, то може виявитися, що максимальна лінійно незалежна сукупність власних векторів оператора  не буда утворювати базис лінійного простору, в якому діє оператор не буда утворювати базис лінійного простору, в якому діє оператор  . У зв’язку з цим виникає питання, якими векторами доповнити до базису простору максимальну лінійно незалежну сукупність власних векторів, щоб у цьому базисі матриця мала найпростіший вигляд. Відповідь на це питання дав французький математик Жордан. . У зв’язку з цим виникає питання, якими векторами доповнити до базису простору максимальну лінійно незалежну сукупність власних векторів, щоб у цьому базисі матриця мала найпростіший вигляд. Відповідь на це питання дав французький математик Жордан.
Вектор  називається приєднаним вектором оператора називається приєднаним вектором оператора  , що відповідає кратному власному значенню , що відповідає кратному власному значенню  цього оператора, якщо можна вказати таке натуральне число цього оператора, якщо можна вказати таке натуральне число  , що , що  . Число . Число  називається порядком приєднаного вектора називається порядком приєднаного вектора  . Нехай . Нехай  – приєднаний вектор порядку – приєднаний вектор порядку  , що відповідає власному значенню , що відповідає власному значенню  . Позначимо через . Позначимо через  вектор вектор  . Тоді за означенням приєднаного вектора . Тоді за означенням приєднаного вектора  або або  . Вектор . Вектор  виявляється власним вектором оператора виявляється власним вектором оператора  . Цю властивість приєднаного вектора можна використовувати при побудові приєднаних векторів за заданим власним вектором . Цю властивість приєднаного вектора можна використовувати при побудові приєднаних векторів за заданим власним вектором  . .
Теорема 5.4. (теорема Жордана). У  -мірному векторному просторі -мірному векторному просторі 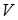 існує базис існує базис 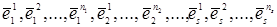 , побудований із , побудований із 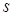 власних векторів власних векторів  і відповідних їм приєднаних векторів, такий, що і відповідних їм приєднаних векторів, такий, що
 , ,  ; ;  , ,  . .
У цьому базисі матриця оператора  має наступний вид має наступний вид
 , ,
де  - квадратна матриця порядку - квадратна матриця порядку  (клітка Жордана): (клітка Жордана):
 . .
Вказана в теоремі 5.4 форма матриці  оператора оператора  називається жордановою або канонічною формою матриці цього оператора. називається жордановою або канонічною формою матриці цього оператора.
На кінець відмітимо, що якщо  – власний вектор лінійного оператора – власний вектор лінійного оператора  , то і вектор , то і вектор  , де , де 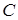 – довільно взяте відмінне від нуля число, також буде власним вектором оператора – довільно взяте відмінне від нуля число, також буде власним вектором оператора  . Дійсно, . Дійсно,
 . .
Приклад 1. З’ясувати, які з перетворень  , заданих шляхом завдання координат вектора , заданих шляхом завдання координат вектора 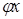 як функцій координат вектора як функцій координат вектора 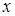 , являються лінійними, і в випадку лінійності знайти їх матриці в тому базисі, в якому задано координати векторів , являються лінійними, і в випадку лінійності знайти їх матриці в тому базисі, в якому задано координати векторів 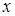 і і 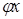 . .
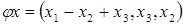 . .
Розв’язання: Для того, щоб дізнатись, чи являються лінійними функції координат вектора треба перевірити, чи виконуються наступні дві аксіоми:
Аксіома адитивності:  . .
Для будь-яких векторів  та та  повинно виконуватись повинно виконуватись
 . .
 
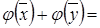 
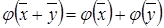 . .
Аксіома адитивності виконується.
Перевіримо аксіому однорідності:

 


Так як властивість адитивності і однорідності виконується, тому перетворення  – лінійне. – лінійне.
Приклад 2. З’ясувати, які з перетворень  , заданих шляхом завдання координат вектора , заданих шляхом завдання координат вектора 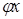 як функцій координат вектора як функцій координат вектора 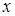 , являються лінійними, і в випадку лінійності знайти їх матриці в тому базисі, в якому задано координати векторів , являються лінійними, і в випадку лінійності знайти їх матриці в тому базисі, в якому задано координати векторів 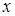 і і 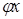 . .
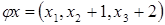 . .
Розв’язання: Для того, щоб дізнатись, чи являються лінійними функції координат вектора треба перевірити, чи виконуються наступні дві аксіоми:
Аксіома адитивності:  . .
Для будь-яких векторів  та та  повинно виконуватись повинно виконуватись


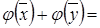 
 . .
Так як властивість адитивності не виконується, тому перетворення  – не лінійне. – не лінійне.
Приклад 3. Показати, що множення квадратних матриць другого порядку а) зліва, б) з права на дану матрицю 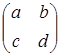 являються лінійними перетвореннями простору всіх матриць другого порядку, і знайти матриці їх перетворень в базисі, який складається з матриць: являються лінійними перетвореннями простору всіх матриць другого порядку, і знайти матриці їх перетворень в базисі, який складається з матриць:
 , ,  , ,  , , 
Розв’язання: За означенням матриці лінійного перетворення  , ,  . Знаходимо образи базисних векторів і обчислюємо їх координати в заданому базисі: . Знаходимо образи базисних векторів і обчислюємо їх координати в заданому базисі:




Розташувавши отримані координати образів за стовпчиками отримаємо матрицю лінійного перетворення:
 . .
Приклад 4. Лінійне перетворення  в базисі в базисі 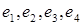 має матрицю має матрицю
A=
Знайти матрицю цього ж перетворення в базисі: e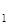 , ,  , ,  , ,  + +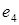 . .
Розв’язання: Формула зв’язку між векторами старого і нового базисів у матричному записі має вигляд:
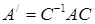
Обернену матрицю знайдемо за допомогою приєднаної:
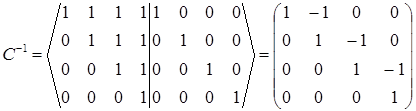
Підставляємо отримані значення в формулу, отримаємо:
 . .
Приклад 5. Знайти власні значення і власні вектори лінійного перетворення, заданому в деякому базисі матрицею:  . .
Розв’язання: Складаємо характеристичне рівняння і розв’язавши його знаходимо власні числа:

Розв’язуємо її методом Гауса, для цього приводимо матрицю до східчастого вигляду:


Складаємо однорідну систему рівнянь для визначення власних векторів:
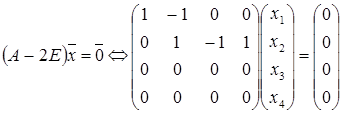

Оскільки максимальна кількість лінійно незалежних власних векторів менша за вимірність простору, то власні вектори не утворюють базис простору і таким чином матриця не діагоналізуєма.
Приклад 6. З’ясувати, яку з матриць лінійних перетворень можна привести до діагонального виду шляхом переходу до нового базису. Знайти цей базис і відповідну йому матрицю: 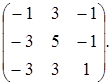
Розв’язання: Складаємо характеристичне рівняння і розв’язавши його знаходимо власні числа:

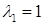
Розв’язуємо її методом Гауса, для цього приводимо матрицю до східчастого вигляду:
A=
Власні вектори мають вигляд:  . . 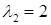
 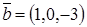 , , 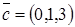
Формула зв’язку між векторами старого і нового базисів у матричному записі має вигляд:
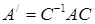
 . .
Матриця діагоналізована.
Приклад 7. З’ясувати, яку з матриць лінійних перетворень можна привести до діагонального виду шляхом переходу до нового базису. Знайти цей базис і відповідну йому матрицю: 
Розв’язання: Складаємо характеристичне рівняння і розв’язавши його знаходимо власні числа:


Розв’язуємо її методом Гауса, для цього приводимо матрицю до східчастого вигляду:
A=

A=
Матриця не може бути діагоналізованою, так як а.к.=г.к.=1.
Висновки
В даній курсовій роботі розглянуто базові властивості лінійних операторів, поняття матриці лінійного оператора та питання зв’язку матриць оператора у різних базисах. Крім того, до роботи включені питання діагоналізіруємості матриці оператора, які пов’язані з існуванням базису, що складається з власних векторів оператора. За усіма розглянутими теоретичними питаннями зроблена підборка задач, яка їх ілюструє та допомагає детально розібратися в теоретичному матеріалі.
оператор вектор лінійний матриця базис
Перелік посилань
1. Курош А.Г. Курс вищої алгебри. – М.: Наука, 1968. – 331 с.
2. Кострикін А.И., Манін Ю.И. Лінійна алгебра і геометрія. – М.: Наука, 1986. – 304 с.
3. Проскуряков І. В. Збірник задач з лінійної алгебри. – М.: Наука, 1974. – 384 с.
|

 ,
, 
 .
.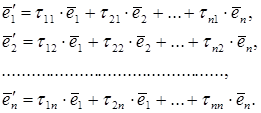
 ,
,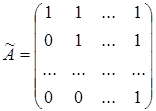 ,
, ,
,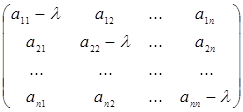 .
. .
. ,
, .
.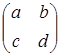 являються лінійними перетвореннями простору всіх матриць другого порядку, і знайти матриці їх перетворень в базисі, який складається з матриць:
являються лінійними перетвореннями простору всіх матриць другого порядку, і знайти матриці їх перетворень в базисі, який складається з матриць: ,
,  ,
,  ,
, 
 . Знаходимо образи базисних векторів і обчислюємо їх координати в заданому базисі:
. Знаходимо образи базисних векторів і обчислюємо їх координати в заданому базисі:



 .
.
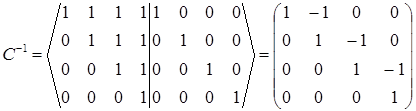
 .
. .
.

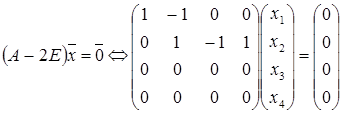
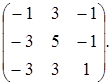



 .
.


