Курсовая работа
"Анализ пьезокерамического преобразователя"
Введение
Устройства, преобразующие электрическую энергию в акустическую (энергию упругих колебаний среды) и обратно называют электроакустическими преобразователями (ЭАП). В зависимости от направления преобразования существуют два вида: излучатели и приёмники. ЭАП широко используют для излучения и приёма звука в технике связи и звуковоспроизведения, для измерения и приёма упругих колебаний в ультразвуковой технике, гидролокации и в акустоэлектронике. Наиболее распространённые ЭАП линейны, т.е. удовлетворяют требованию неискажённой передачи сигнала, и обратимы, т.е. могут работать и как излучатель, и как приёмник, и подчиняются принципу взаимности.
В большинстве случаев имеет место двойное преобразование энергии: электромеханическое, в результате которого часть подводимой к преобразователю электрической энергии переходит в энергию колебаний некоторой механической системы, и механоакустическое, при котором за счёт колебаний механической системы в среде создаётся звуковое поле. ЭАП – это своеобразные связанные колебательные системы. В такой системе происходит взаимодействие электрических и механических процессов. Потому и эквивалентные схемы ЭАП представляют в виде двух связанных контуров – механического и электрического. В физике существует метод электромеханических аналогий, с помощью которого получают эквиваленты электрических и механических величин.
Данный метод основан на подобии математических моделей механических и электрических систем. Уравнения движения механических систем и уравнения напряжений и токов в электрических цепях принимают за математические модели, а построенная с использованием электрических элементов – аналогов эквивалентная механической системе электрическая схема предстает как графическое изображение уравнения движения. Граничные условия в схеме выглядят в виде источников и потребителей энергии.
1.
Теоретическая часть
1.1 Пьезоэффект. Общие положения
В некоторых диэлектриках и полупроводниках под действием деформаций в определенных направлениях появляются электрические заряды, то есть они поляризуются. Это явление, названное прямым пьезоэффектом, было обнаружено у кристаллов кварца, турмалина, сегнетовой соли, и др.
Под действием внешнего электрического поля в пьезоэлектрике изменяется взаимное расположение атомов решетки, а, следовательно, и размеры кристалла. При действии внешней силы, деформирующей кристалл, также изменяется расположение атомов решетки, в результате чего внутри кристалла меняется электрическое поле и появляется поляризация у всего кристалла, а между электродами – разность потенциалов.
Деформацию диэлектрика, т.е. изменение его размеров под действием электрического поля, называют обратным пьезоэффектом. Таким образом, если на металлические обкладки подать переменное напряжение, то пластинка будет попеременно растягиваться и сжиматься вдоль оси  , т.е. в ней будут возбуждаться механические колебания. , т.е. в ней будут возбуждаться механические колебания.
1.2 Уравнения пьезоэффекта
Важно отметить, что приведенные соотношения имеют лишь качественный характер. Реальное описание пьезоэлектрического эффекта намного сложнее. Дело в том, что механическое напряжение является тензорной величиной, имеющей шесть независимых компонентов, тогда как поляризация является векторной величиной. Поэтому пьезомодуль, устанавливающий связь между вектором поляризации и механическими напряжениями, является тензором третьего ранга, имеющим 18 независимых компонентов. В тензорной форме уравнение прямого и обратного пьезоэффектов принимает следующий вид:
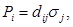 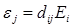
где i
= 1,2,3
– компоненты вектора поляризованности; j
= 1,2…6
– компоненты тензора механических напряжений или деформаций.
При пьезоэлектрическом эффекте возникшее в кристалле электрическое поле можно охарактеризовать вектором электрической поляризации Р, вектором электростатической индукции в или вектором Е, а действующее на кристалл механическое усилие – тензором механических напряжений Тij или тензором механических деформаций еij. Таким образом, тензорное воздействие вызывает векторное явление, или обратно. Значит, связывающее их свойство кристалла должно быть тензором третьего ранга:

В общем случае (без учёта влияния симметрии кристалла) каждая компонента вектора Р связана с каждой компонентой тензора Тij
соотношением:


Входящие в это уравнение 27 компонент образуют тензор третьего ранга – тензор пьезоэлектрических модулей. Вследствие симметрии тензора механических напряжений Тij его компоненты Поэтому: Поэтому:  и число независимых компонент тензора сокращается до 18. Компактные матричные обозначения вводятся по схеме: 11 → 1, 22 → 2, 33→ 3, 23
или 32 → 4, 13
или 31 → 5, 12
или 21 → 6.
Для и число независимых компонент тензора сокращается до 18. Компактные матричные обозначения вводятся по схеме: 11 → 1, 22 → 2, 33→ 3, 23
или 32 → 4, 13
или 31 → 5, 12
или 21 → 6.
Для  примем обозначения: примем обозначения:  , тогда: , тогда:


Таблица 1. Матрица пьезомодулей

Чтобы определить физический смысл каждой из этих компонент рассмотрим одну из компонент, например d
14:
d
14 =
d
123 +
d
132
, т.е. P
1 = (
d
123 +
d
132)
T
23
. Если в кристалле d14 ≠ 0, то это значит, что под действием сдвигового напряжения, приложенного в направлении оси Х2
к площадке, нормальной к оси Х3
(или в направлении Х3
к площадке, нормальной к Х2
), возникает электрическая поляризация, характеризуемая составляющей вектора Р1
, направленная вдоль оси Х1
.
Данный смысл пьезомодуля d
14
изменится, если изменить кристаллографическую установку. Проанализировав таким образом все 18 пьезомодулей, можно прийти к выводу, что они характеризуют четыре типа пьезоэлектрических эффектов.
Уравнение ППЭ можно выразить через относительную деформацию 
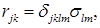
где 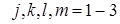 – компоненты тензора деформации упругой податливости кристалла. – компоненты тензора деформации упругой податливости кристалла.
Тогда уравнение ППЭ примет вид
 , ,
где  – компоненты пьезоэлектрического коэффициента третьего ранга, также как и – компоненты пьезоэлектрического коэффициента третьего ранга, также как и 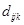 . Он также характеризуется пьезоэлектрическими свойствами кристалла. . Он также характеризуется пьезоэлектрическими свойствами кристалла.
ППЭ можно характеризовать не только через поляризацию 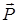 , но и через вектор напряженности электрического поля , но и через вектор напряженности электрического поля 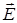
 
где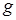 и и 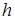 – пьезоэлектрические коэффициенты кристалла, связанные между собой, а также с коэффициентами – пьезоэлектрические коэффициенты кристалла, связанные между собой, а также с коэффициентами 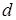 и и 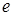 через упругие и диэлектрические постоянные. через упругие и диэлектрические постоянные.
Основное уравнение обратного пьезоэффекта (ОПЭ) имеет вид

где величина 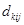 – это компоненты тензора третьего ранга идентичного тензору пьезомодулей, входящих в основное уравнение пьезоэффекта. – это компоненты тензора третьего ранга идентичного тензору пьезомодулей, входящих в основное уравнение пьезоэффекта.
1.3 Пьезокерамические преобразователи и эквивалентные схемы
В пьезокерамических элементах (ПКЭ) разных геометрических форм можно возбудить линейные или планарные нормальные колебания в различных направлениях. Типы нормальных колебаний, называемые модами колебаний, в ПЭК зависят от взаимной ориентации оси поляризации, электрического поля и колебательного перемещения частиц. По взаимной ориентации электрического поля и колебательного перемещения выделяют моды колебаний, в которых электрическое поле поперечно направлению колебаний (пьезоэлектрически мягкие моды) или совпадают с ними (пьезоэлектрически жесткие моды).
Для выбора независимых электрических переменных (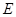 или или  ) в уравнениях пьезоэффекта оценивают электрические граничные условия в направлениях одномерного линейного или планарного колебательного движения. Электрические граничные условия определяются расположением поверхностей электродов и формой ПКЭ. ) в уравнениях пьезоэффекта оценивают электрические граничные условия в направлениях одномерного линейного или планарного колебательного движения. Электрические граничные условия определяются расположением поверхностей электродов и формой ПКЭ.
Для пьезомягких мод поверхности электродов параллельны направлению колебаний (используется поперечный пьезоэффект): 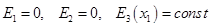 , поэтому независимой электрической переменной целесообразно выбрать , поэтому независимой электрической переменной целесообразно выбрать 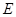 . Входящая в этом случае в соответствующие уравнения состояния упругая константа с индексом . Входящая в этом случае в соответствующие уравнения состояния упругая константа с индексом 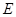 свободна от дополнительного вклада, связанного с пьезоэффектом, при этом свободна от дополнительного вклада, связанного с пьезоэффектом, при этом 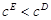 . Отсюда ясно, почему моды с полем . Отсюда ясно, почему моды с полем 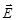 , поперечным колебаниям перемещения, называют пьезомягкими. , поперечным колебаниям перемещения, называют пьезомягкими.
Для пьезожестких мод поверхности электродов перпендикулярны направлению колебаний (используется продольный пьезоэффект): 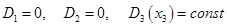 , поэтому независимой переменной целесообразно выбрать , поэтому независимой переменной целесообразно выбрать 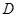 . .
Механические граничные условия для одномерных или планарных мод колебаний формулируются в зависимости от того, какой размер определяет резонансную частоту: наибольший или наименьший. Моды колебаний по этому признаку разделяются на низкочастотные и высокочастотные. Промежуточные моды выделяют как среднечастотные.
1.4 Дисковый пьезокерамический преобразователь
Для проведения гидроакустических измерений необходимы излучатели и приемники звука, удовлетворяющие требованиям неискаженного звукового поля, широкого частотного диапазона, отсутствия направленности действия.
Пьезокерамический дисковый преобразователь (рис. 1) состоящий из металлического диска 1 и двух приклеенных к нему круглых пьезокерамических биморфных пластин 2, колебательная система помещена в корпус 3, нижняя пластинка – в заливочную массу 4.

Рис. 1. Пьезокерамический дисковый преобразователь

Рис. 5. Эквивалентная схема дискового пьезокерамического ЭАП
где:
Сs – электрическая емкость преобразователя;
R – сопротивление электрических потерь;
N – коэффициент электромеханической трансформации;
СЭ
– эквивалентная гибкость;
MЭКВ
– эквивалентная масса;
RS
– сопротивление излучателю;
Rмп
– сопротивление механических потерь.
2.
Расчетная часть
2.1 Постановка задачи
Диск, изготовленный из пьезоматериала ЦТСНВ-1, имеет средний радиус а=4 см. Учитывая, что толщина дискаd=a/5
– определим элементы электромеханической схемы, включая коэффициент трансформации N, сопротивление излучения Rs, сопротивление электрических потерь Rпэ, сопротивление механических потерь Rмп;
– найдем конечные формулы для КЭМС и КЭМСД и рассчитаем их;
– определим частоты резонанса и антирезонанса;
– вычислим добротность преобразователя в режиме излучения;
– рассчитаем и построим частотные характеристики входной проводимости и входного сопротивления.
Геометрические размеры диска:
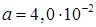 м –
средний радиус диска; м –
средний радиус диска;
 м
– толщина диска. м
– толщина диска.
Константы пьезокерамического материала ЦТСНВ-1:
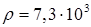 кг/м3
– плотность; кг/м3
– плотность;
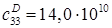 Н/м2
– модуль упругости; Н/м2
– модуль упругости;
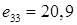 Кл/м2
– пьезоэлектрическая постоянная; Кл/м2
– пьезоэлектрическая постоянная;
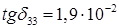 – тангенс угла электрических потерь; – тангенс угла электрических потерь;
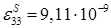 Ф/м
– диэлектрическая проницаемость. Ф/м
– диэлектрическая проницаемость.
Свойства воды:
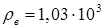 кг/м3
– плотность; кг/м3
– плотность;
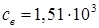 м/с
– скорость звука в воде. м/с
– скорость звука в воде.
Акустомеханический КПД преобразователя:
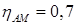 . .
2.2 Расчет параметров ЭАП
1. Эквивалентная масса
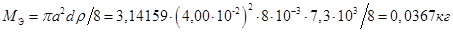
2. Эквивалентная податливость
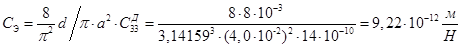
3. Электрическая емкость
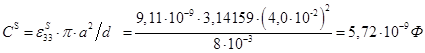
4. Коэффициент электромеханической трансформации
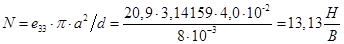
5. Собственная частота

6. Активное сопротивление излучения

7. Активное сопротивление, учитывающее потери энергии
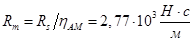
8. Активное сопротивление механических потерь
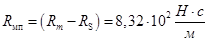
9. Коэффициент электромеханической связи
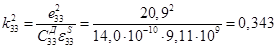
10. Резонансная частота
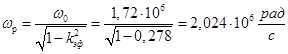
11. Частота антирезонанса
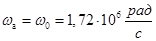
12. Добротность в режиме излучения
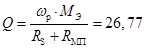
2.3 Расчет и построение частотных характеристик входной проводимости и входного сопротивления
Для емкостных ЭАП с элементами 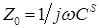 и и 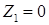 активная и реактивная проводимость выражаются следующим образом активная и реактивная проводимость выражаются следующим образом
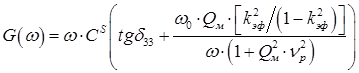 , (3) , (3)
пьезоэффект преобразователь частотный сопротивление
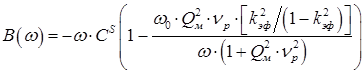 , (4) , (4)
где 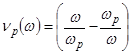 . Произведем замену . Произведем замену  , тогда , тогда
 . (5) . (5)
Подставив (5) в (3) и (4) с учетом замены получим
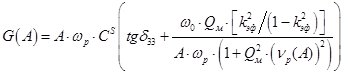 , ,
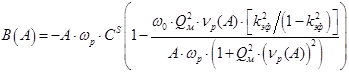 . .
Таким образом, комплексная проводимость имеет вид:
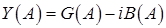 . .
На рис. 4 представлены графики зависимостей 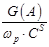 , , 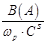 , , 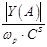
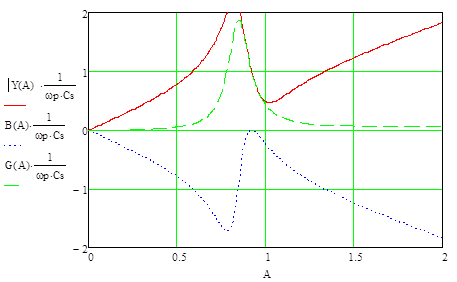
Рис. 4. Частотная характеристика проводимости емкостного ЭАП
Комплексное сопротивление в зависимости от относительной частоты имеет вид
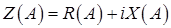 , ,
где активное и реактивное сопротивление связано с активной и реактивной проводимостью следующими соотношениями
На рис. 5 представлены графики зависимостей 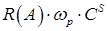 , , 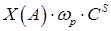 , , 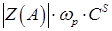 . .
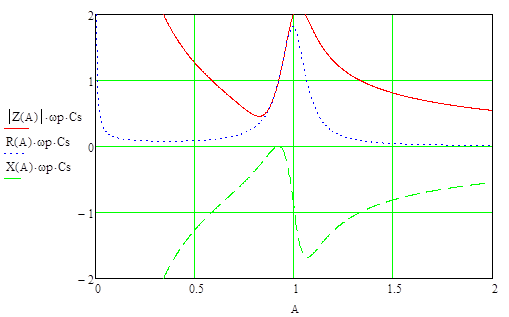
Рис. 5. Частотная характеристика входного сопротивления емкостного ЭАП
Заключение
В работе были определены элементы электромеханической схемы, частоты резонанса и антирезонанса, расчет значения КЭМС, вычисление добротности преобразователя в режиме излучения, расчет и построение частотных характеристик входной проводимости и входного сопротивления.
В процессе анализа графиков стало понятно, что данная система является резонансной и имеет четко выраженный резонанс и антирезонанс. Из полученного значения коэффициента электромеханической связи 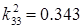 можно сделать вывод о большом КПД системы. можно сделать вывод о большом КПД системы.
Из построенного графика можно сделать заключение, что существует возможность определения резонансной и антирезонансной частоты и определение резонансного промежутка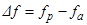 . Причем, чем выше . Причем, чем выше 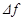 , тем выше будут проявляться керамические свойства материала. , тем выше будут проявляться керамические свойства материала.
Список использованных источников
1. Пугачев С.И. Конспект лекций по курсу ЭАП.
2. Резниченко А.И. Подводные электроакустические преобразователи. Л.: ЛКИ, 1990.
3. Свердлин Г.М. Гидроакустические преобразователи и антенны. Л.: Судостроение, 1988.
|