| ЗМІСТ
ОСНОВНІ УМОВНІ ПОЗНАЧЕННЯ
ВСТУП
1. ТЕОРЕТИЧНА ЧАСТИНА
1.1 Методи дослідження рівноваги в гетерогенних системах
1.1.1 Основні положення
1.1.2 Система Р – Т
1.1.3 Система Г – Р
1.1.4 Система Г-Р-Т
1.1.5 Система Г-Т
1.2 Дослідження кінетики масообміну
1.2.1 Специфіка вивчення кінетики хімічних реакцій
1.2.2 Методи вивчення кінетики гетерогенно-каталітичних реакцій (системи Г-Т
і Р-Т
)
1.2.3 Основи формальної кінетики. Швидкість хімічної реакції
1.2.4 Кінетична модель топохімічних реакцій
1.3 Методи розрахунків
1.3.1 Інтегральні методи розрахунку кінетичних констант
1.3.1.1 Одинична реакція першого порядку
1.3.1.2 Одинична реакція другого порядку
1.3.1.3 Одинична реакція n-го порядку
1.3.1.4 Метод графічної інтеграції
1.3.1.5 Метод постійних частин
1.3.2 Оцінка застосовності теоретичних рівнянь
1.3.3 Розрахунок енергії активації
2. ПРАКТИЧНА ЧАСТИНА
2.1 Постановка завдання
2.2 Виконання завдання
ВИСНОВОК
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
гетерогенна кінетика хімічна реакція
О
СНОВНІ УМОВНІ ПОЗНАЧЕННЯ
V
- швидкість реакції;
C
– концентрація регента;
τ – час;
k
–
константа швидкості реакції;
K
- коефіцієнт масопередачі;
F
- поверхня розділу фаз;
ΔC
- рушійна сила процесу;
N –
кількість речовини;
β
– ступінь перетворення;
τ
1/2
- час напівперетворення;
α
– ступінь напівперетворення;
Е – енергія активації.
ВСТУП
Курсова робота на тему «Методи експериментальних досліджень і розрахунків кінетики хіміко-технологічних процесів» з дисципліни «Хімічна технологія неорганічних речовин».
Курсова робота виконується з метою засвоєння на практиці основних методів дослідження стану рівноваги і кінетики хіміко-технологічних процесів, основ розрахунку кінетичних констант, визначення механізму і області протікання процесів.
Вивчення даної дисципліни ґрунтується на знаннях, одержаних при вивченні таких дисциплін: загальна і неорганічна хімія, фізична хімія, фізика, вища математика, теоретичні основи технології неорганічних речовин, кінетика і каталіз, основи наукових досліджень і наукова інформація і інших.
Мета і задачі курсової роботи:
- засвоєння на практиці основних методів дослідження стану рівноваги і кінетики хіміко-технологічних процесів;
- засвоєння основ розрахунку кінетичних констант;
- визначення механізму і області протікання процесів.
1. ТЕОРЕТИЧНА ЧАСТИНА
1.1 Методи дослідження рівноваги в гетерогенних системах
1.1.1 Основні положення
Інформація про рівновагу є первинною при створенні технологічного процесу. В гомогенних системах, термодинаміка яких детально розроблена, вона може бути одержана і розрахунковим шляхом за методами які розглядаються в курсах «Фізична хімія» та «Теоретичні основи технології неорганічних речовин». В гетерогенних системах її дуже часто визначають тільки дослідним шляхом.
Для дослідження рівноваги в гетерогенних системах використовують дві групи базових методів: статичні і динамічні. В статичних методах завантажені в реактор реагенти витримують до встановлення рівноваги, не обновлюючи. Динамічні методи, або проточні - це методи з реагентами, які в ході досліду вводять в реактор і виводять з нього, замінюючи свіжими. Широке поширення набули також комбіновані методи: статичні по одній фазі (наприклад, по рідкій) і динамічні по іншій (наприклад, по газу). В циркуляційних методах динамічний принцип роботи поєднується з відсутністю введення свіжих реагентів, що характерне для методів статичних. Вони, отже, є варіантом статичного методу. Схемне зображення методів, вживаних при вивченні гетерогенної рівноваги, приведено на рис.1.

Рис. 1. Схематичне зображення методів:
а – статичний метод;
б – метод статичний з зовнішньою циркуляцією однієї з фаз (циркуляційний); в – динамічний метод;
г – комбінований метод (проток однієї з фаз відсутній)
Збільшенню швидкості перебігу процесу сприяє диспергування і перемішування фаз. Обидва прийоми підвищують швидкість перенесення компонентів системи до поверхні розділу фаз. Диспергування припускає попереднє подрібнення частинок твердої фази і введення газу в рідину через дисперсійні перегородки (наприклад, фільтр Шотта). Можливості диспергування небезмежні, і в лабораторних умовах одержати пил або міхур газу розміром істотно нижче 0,1 мм
важко. Принципи перемішування очевидні з рис.1: мішалка (а), циркуляція (б), протока (в, г).
Диспергування і перемішування – це, у відомому значенні, турбування експериментатора про самого себе: чим вище швидкість встановлення рівноваги, тим швидше буде завершений дослід. Контроль перебігу процесу в часі - це борг експериментатора. Але, без "виплати" його немає, і не може, бути вивчення рівноваги, оскільки не яке окреме вимірювання виконане через будь-який, навіть дуже значний, проміжок часу після початку досліду, не має в собі самому ознаки рівноваги. Воно одержує це через зіставлення з іншими вимірюваннями, у тому числі, з вимірюваннями, що здійснені через інші (і великі, і менші) проміжки часу.
У багатофазній системі число ступенів свободи, що визначають стан рівноваги, дається рівнянням Гиббса - Дюгема:
У = К - Ф+2
де: У
- число ступенів свободи
К
- кількість компонентів
Ф
- число фаз
2
– ступені свободи, що доводяться на "постійні" термодинамічні параметри: температуру і тиск.
Це ж рівняння, по суті, визначає кількість незалежних змінних в дослідах по вивченню рівноваги. Наприклад, для чотирьох компонентів, що відповідає реакції:
А + В
«
С + Д
і двох фаз кількість незалежних змінних рівна чотирьом. До них слід віднести температуру, тиск і концентрації двох будь – яких компонентів. Цю сукупність змінних позначають через Т
, Р
і Сij
(i
- номер компоненту, j
-
номер фази) і називають термодинамічними параметрами системи. Кожний дослід по вивченню рівноваги здійснюють в деякій точці багатовимірного простору, утвореного цими параметрами. Рухаючись по ньому з вибраною стратегією (наприклад, відповідно до правил статистичного планування, які розглядаються в курсі “Математичне моделювання і застосування ЕОМ”), дослідник здійснює більш менш повне вивчення об'єкту. Нижче розглядається техніка вивчення гетерогенної рівноваги в системах, що найбільш часто зустрічаються в неорганічній технології. Фази систем позначені заголовними буквами: Г
- газ, Р
- рідина, Т
- тверде тіло.
1.1.2 Система Р – Т
Набір термодинамічних параметрів в цій системі рівний двом найменуванням: Т
і Cij
(оскільки Сij
– може бути набагато більше ніж 1, то говорити про два параметри не можна). Тиск виключений. Він пов'язаний з газовою фазою, яка за умов задачі неістотна. Область зміни температур в технології неорганічних речовин практично обмежується температурами замерзання і кипіння води (або іншого розчинника). Область зміни концентрацій речовини, що розчиняється, обмежується з одного боку нулем (немає речовини в розчині) з другого боку – концентрацією насиченого розчину при заданій температурі (речовина перестає розчинятися). Отже,
Т, Р, Cij
®
Т (0 ÷ 100 0
С),
Cij
(0 ÷ Снас).
Транспорт твердого матеріалу, як правило, ускладнений. В лабораторних умовах використання великих кількостей рідкої фази (водні розчини кислот, солей і лугів) небажане. Сукупність всіх цих обставин призводить до того, що найпереважнішим типом реактора є статичний, схема якого була приведена на рис.1. Він є термостатованою відкритою колбою або стаканом. Реактор обов'язково обладнають мішалками.
У реактор послідовно завантажують твердий матеріал і рідину, включають мішалку і ведуть відлік часу, періодично відбираючи на аналіз рідку фазу. В ході проміжних аналізів звичайно визначають зміст тільки ключового компоненту. Як ключовий компонент, непридатна речовина, що знаходиться в системі у великому надлишку - його концентрація змінюється мало. В цій же якості незручна речовина, концентрація якої дуже низька, оскільки її визначення звичайно ускладнене. Як ключову слід вибирати речовину, для якої зміни концентрації визначаються легко і точно.
Якщо передбачений фізико–хімічний аналіз, то пробу після визначення в ній ключового компоненту повертають в реактор. При хімічному аналізі пробу в реактор не повертають, а спад речовин, звичайно, враховують шляхом складання по-компонентних матеріальних балансів.
Після досягнення рівноваги фази розділяють. Це одна з найважчих операцій методу, особливо якщо вивчення рівноваги проводять при температурі, яка суттєво відрізняється від кімнатної. В ході фільтрації і декантації відбувається зміна температури розчину, що міняє рівноважні співвідношення. Тому ці операції проводять на фільтрах, що обігріваються (охолоджуються), і по можливості швидко. Повне розділення фаз вимагає, крім того, промивки осаду на фільтрі, що може супроводжуватися його частковим розчиненням. Підбору промивної рідини, її кількості, температурі і доцільності її приєднання до основної маси фільтрату надається особлива увага.
Фільтрат аналізують на всі компоненти системи. Аналіз твердої фази, якщо він представляє значні труднощі, в технологічних дослідах часто не проводять. Склад її розраховують на підставі матеріальних балансів компонентів в рідкій фазі.
У неорганічній технології описану вище техніку експериментатор використовує при вивченні сольової рівноваги і процесів екстракції речовин з природної сировини (наприклад, фосфорної кислоти з фосфоритів).
1.1.3 Система Г – Р
Число найменувань термодинамічних параметрів в цій системі дорівнює трьом. Інтервал температур, як і в системі Р - Т
, дорівнює 0 ÷ 100°С. Тому Т, Р, Cij Т( 0 ÷ 100°C), Р(0 ÷ Рзж), Cij(0 ÷ Снас.).Інтервал по тиску у верхній межі обмежується, як правило, тиском зжиження газу, а інтервал по концентраціях – концентрацією насиченого розчину (наприклад, при її підвищенні ми можемо одержати трифазну систему, оскільки розчинена речовина почне кристалізуватися). Для вивчення рівноваги в системі Г - Р
частіше за інші використовують комбінований метод: проточний по газу і статичний по рідині. Його реалізують у вигляді двох варіантів, які можна назвати методом "рівноважного тиску" і методом "рівноважних складів". В методі "рівноважного тиску" летучий компонент переходить з рідини в газову фазу так, щоб в ній досягався парціальний тиск компоненту, рівноважний складу рідини. В методі "рівноважних складів" має місце зворотний перехід. В ньому забезпечують склад рідини, рівноважний парціальному тиску компонентів газової фази.
1.1.4Система Г-Р-Т
У неорганічній технології використовують речовини, які як правило, добре змочувані водою. Тому рівновага в системі Г-Р-Т
зводиться до рівноваги в двох пов'язаних між собою системах: Г-Р
і Р-Т
. Незалежне вивчення кожної з цих систем, якщо воно можливе, дозволяє розрахувати рівноважний стан трифазної системи. Якщо потреба в експериментах все ж таки є, то для їх виконання використовують методи, вживані в системі Г-Р
; вони поєднують в собі елементи, достатні для вивчення будь-якої із зв'язаних двофазних систем. В реакторі, природньо, буде знаходиться суспензія Т
в Р
.
Основна складність будь – якого методу вивчення рівноваги, пов'язана з фіксацією його встановлення. В цій системі вона ускладнена тим, що швидкість встановлення рівноваги в парах, Г-Р
і Р-Т
може виявитися істотно різною. Аналіз на швидкому "плечі" системи може свідчити про встановлення рівноваги, яка насправді не досягнута. Тому контролю рівноваги слід надати підвищену увагу, а аналіз повинен обов'язково захоплювати фази повільного "плеча" системи.
1.1.5 Система Г-Т
Для цієї системи характерний повний набір термодинамічних параметрів, і дуже широкий інтервал їх зміни. Він майже не має обмежень для тиску. Для температури нижньою межею є абсолютний нуль, а верхнім - температура плавлення твердого тіла.
Для вивчення рівноваги в системі Г-Т широко використовують комбінований і статичний методи. Вибір методу в основному обумовлений тиском: при атмосферному і підвищеному тиску застосовують комбіновані установки, для вимірювань у вакуумі - статичні. Дані про рівновагу в системах Г-Т
необхідні для створення процесів кальцинації твердих речовин і адсорбційного очищення газів. Їх використовують і при визначенні величини питомої поверхні адсорбентів і каталізаторів, при вивченні властивостей поверхні твердих тіл і структури пор в них.
1.2 Дослідження кінетики масообміну
Вивчення рівноваги дає необхідну, але для розрахунку технологічного процесу (апарату) недостатню інформацію. Процес протікає в часі, в апараті обмежених розмірів; і кінцевий стан компонентів і фаз, що беруть участь в ньому, відрізняється від асимптотичного (t
®
¥
) рівноважного стану.
Структура математичних моделей більшості сучасних хіміко-технологічних процесів (апаратів) в даний час загалом добре розроблена. Модель звичайно включає рівняння збереження маси і енергії, рівняння їх перенесення між фазами системи, рівняння перетворення компонентів у фазах або на межі їх розділу, дані про граничний (рівноважний) стан системи і умови однозначності. По рівню специфічності рівняння моделі розпадаються на дві групи. До першої відносяться рівняння збереження і умови однозначності. Це специфічні елементи моделей: їх форма залежить від типу і конструкції апарату, їх параметри відображають умови процесу і розміри апарату. Отже, ніщо, пов'язане з цими елементами, не може і не повинне бути пов'язане з експериментом, щонайменш, з лабораторною його стадією.
Специфіка процесу лише опосередковано впливає на рівноважний стан системи: вона задає умови, але не визначає ні форму, ні параметри. Те ж саме можна сказати про рівняння кінетики. Рівняння кінетики і рівноважні співвідношення неспецифічні, не пов'язані з конкретним процесом і апаратом. Саме тому рівновага і кінетика можуть бути предметом експерименту.
Маючи взагалі не специфічність, дані про рівновагу і кінетику, ні в якому разі, нерівноправні в математичних моделях процесів і апаратів. До форми перших ставляться нежорсткі вимоги. Їх можна задати і у вигляді таблиці експериментальних даних. Але без доказів очевидна мала цінність таблиці експериментальних даних за течією в часі ("кінетика") процесу, реалізованого в експериментальному реакторі. Причина полягає в тому, що ця "кінетика" не звільнена від специфіки лабораторного реактора (конструкції, розмірів, умов роботи і т.ін.), яка нетотожна специфіці промислового об'єкту. Усунення специфіки і складає головну задачу експериментатора, що працює на математичне моделювання промислового апарату, і досягається вона через математичне моделювання об'єкту експериментування. Подібне, дійсно, пізнається подібним.
Математичне моделювання експериментального об'єкту - невід'ємна частина дослідів, метою яких є забезпечення проектних робіт із створення нових виробництв. Воно багато в чому визначає конструкцію експериментальної установки і методологію виконання дослідів. Втім, справедливе і більш звичне зворотне твердження: установка і дослід визначають структуру і зміст математичної моделі.
1.2.1 Специфіка вивчення кінетики хімічних реакцій
Вивчення кінетики хімічних реакцій це більш складніший етап дослідницької роботи, ніж вивчення масообміну: зростає число належних до визначення коефіцієнтів, складнішою стає підтримка постійної температури, більш жорсткими стають вимоги до рівня ізотермічності. Цілком нездійсненною може виявитися умова постійності розділу фаз: саме протікання реакції може бути пов'язано з руйнуванням старих фаз і виникненням нових. Вивчення хімічних реакцій часто виявляється справою швидше мистецтва, ніж логіки.
Порівняно простий випадок представляє кінетика гетерогенних каталітичних реакцій. В ході них каталізатор у взаємодії як би не бере участь. Такі реакції називають квазігомогенними. Техніка їх вивчення розроблена достатньо добре.
Хімічна реакція, навіть гомогенна, є звичайно складним багатоступінчатим процесом. Розшифровка її механізму, підсумком якого є пізнання природи реакції і визначення фізично достовірних параметрів кінетики її протікання, є дуже складною задачею. Тому в технологічних дослідженнях кінетику реакцій часто розглядають формально, швидкість яких виражають у формі закону діючих мас. Реакції, які вдається описати таким чином, називають простими.
1.
2.2 Методи вивчення кінетики гетерогенно-каталітичних реакцій (системи Г-Т
і Р-Т
)
Формально каталізатор не бере участі в перетвореннях, і каталітична реакція, як вже наголошувалося, є квазігомогенною. Тому в рівняннях математичної моделі присутні тільки концентрації реагенту в потоці.
Для вивчення кінетики каталітичних реакцій використовують реактори трьох типів (три метода): інтегральний, диференційний і циркуляційний.
У зовнішньо-кінетичній області реакція переважно протікає на поверхні каталізатора. Дифузія з потоку до поверхні більш не лімітує процес, а дифузія реагенту в глиб зерна каталізатору виключена, наприклад, через те, що каталізатор непористий. Порядок швидкості реакції так само, як константа швидкості і енергія активації, у зовнішньо-кінетичній області визначають саму хімічну реакцію і є кінцевим результатом дослідження формальної кінетики процесу, що вивчається.
Зовнішньо-кінетична область протікання процесу може спостерігатися і на пористих каталізаторах. Це звичайно має місце тоді, коли швидкість реакції така висока, а коефіцієнт дифузії реагенту в гранулу такий малий, що реагент зазнає перетворення, не встигаючи скільки-небудь помітно дифундувати в глиб гранули, тобто він реагує на її поверхні.
Частіше ж в пористій гранулі спостерігають внутрішньо-дифузійну і внутрішньо-кінетичну області протікання реакції. Розглянемо умови, протилежні умовам протікання зовнішньо - кінетичного процесу: швидкість реакції дуже мала, а комплекс для реакції дуже великий. Із-за великої проникності гранули каталізатора весь об'єм її пронизаний реагентом. Концентрація реагенту на поверхні гранули і в будь-якій крапці усередині неї практично однакові. Реакція з однаковою швидкістю протікає у всьому об'ємі пористого каталізатора. Такий режим і називають внутрішньо-кінетичним. Його характерна ознака, що констатується експериментатором, полягає в незалежності константи швидкості від розміру гранули, якщо цей розмір змінюється у бік зменшення. І фізично, і по здоровому глузду це зрозуміло: якщо в "великій" гранулі градієнт концентрацій був відсутній, то в малій він свідомо спостерігатися не буде. Константа швидкості, порядок реакції і енергія активації, визначені в дослідах, у внутрішньо-кінетичній області відображають перебіг самої хімічної реакції.
Зовнішньо-кінетична і внутрішньо-кінетична області - це, якщо можна так сказати, крайні крапки на шкалі можливих режимів реакції. "Попасти в точку" - маловірогідний успіх для експериментатора. Звичайно він має справу зі всією шкалою режимів, в яких одночасно виявляється вплив і процесів перенесення речовини усередині гранули, і його перетворення. Ця широка область носить назву внутрішньо-дифузійної. Для зовнішньо-кінетичного процесу гранула як би непрозора, і реагент усередині неї відсутній. При внутрішньо-кінетичному - гранула володіє ідеальною проникністю: у всьому об'ємі її концентрація реагенту однакова, і з однією і тією ж швидкістю протікає хімічна реакція. Розподіл концентрацій у внутрішньо - дифузійній області або, як то кажуть, глибина проникнення реакції в гранулу, залежить від співвідношення між швидкістю реакції і швидкістю дифузії реагенту. Відносно висока швидкість реакції - реагент перетворюється, не встигнувши про дифундувати углиб, реалізується майже зовнішньо-кінетичний режим. І навпаки, відносно висока швидкість дифузії - реагент встигає, хоч і нерівномірно, розподілитися за об'ємом гранули, реалізується майже внутрішньо-кінетичний режим. Змінюючи розмір гранули каталізатора, експериментатор, що вивчає перебіг хімічної реакції, переводить процес з "незручної" внутрішньо-дифузійної області в зручніші зовнішньо і внутрішньо-кінетичні. Збільшення діаметру приведе до зрушення в область зовнішньо - кінетичну, зменшення - в область внутрішньо кінетичну. Але можливості експериментатора і його апаратура обмежені і часто експериментальний перехід в "чисті" області виявляється неможливим. Доводиться вдаватися до розрахункового апарату, що дається теорією макрокінетики каталітичних реакцій, і визначати значення параметрів, що характеризують хімічну реакцію, із значень, знайдених в дослідах для змішаної внутрішньо-дифузійної області протікання процесу. Вивчаючи процес при різних швидкостях потоку, при різних температурах і на зернах різного розміру, експериментатор встановлює область протікання реакції і міняє ці умови так, щоб підвищити "якість" шуканих параметрів в ході самого експерименту або в ході подальших розрахунків.
1.2.3 Основи формальної кінетики. Швидкість хімічної реакції
При протіканні реакції:
 (1)
(1)
зліва направо концентрація речовин А
1
і А
2
зменшується, а концентрація речовин А3
і А4
збільшується.
Швидкість реакції (1) визначається зміною концентрації реагентів в одиницю часу. Для реакцій, що протікають при постійному об'ємі в закритих системах, швидкість реакції виражають рівнянням
 (2) (2)
де vi
і Сi
— відповідно стехіометричний коефіцієнт і концентрація i-го реагенту у момент часу τ.
Швидкість реакції завжди позитивна. Тому в рівнянні швидкості реакції (2) ставлять знак плюс, якщо швидкість реакції визначають по зміні концентрації кінцевої речовини в одиницю часу, і знак мінус, якщо швидкість визначається по зміні концентрації початкової речовини.
Згідно закону дії мас швидкість реакції V
пропорційна твору концентрацій реагуючих речовин в ступенях, рівних їх стехіометричним коефіцієнтам в рівнянні швидкості реакції. Для елементарної реакції (1), що протікає зліва направо (пряма реакція), швидкість реакції V
виражається рівнянням
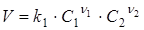 (3) (3)
де k1
— коефіцієнт пропорційності — константа швидкості прямої реакції;
С1
і C
2
— концентрації речовин A
1
і А2
.
Таким чином, рівняння швидкості масопередачи для гомогенного процесу може бути представлено у вигляді
 (4) (4)
Рівняння швидкості масопередачи гетерогенних процесів
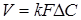 (5) (5)
де k
- коефіцієнт масопередачи;
F
- поверхня розділу фаз;
ΔC
- рушійна сила процесу.
Коефіцієнт масопередачи - це кількість речовини в кілограмах, передана з однієї фази в іншу через поверхню зіткнення фаз, яка дорівнює 1 м2
,
при рушійній силі процесу, рівній 1 кг/м3
, протягом 1 години
. При цьому розмірність коефіцієнта масопередачи буде м/год
. Коефіцієнт масопередачи в гетерогенному процесі складна величина, залежна не тільки від хімічних властивостей реагуючих речовин, але і від їх фізичних властивостей, швидкостей потоків, ступеня перемішування, а у ряді випадків від конструктивного оформлення реактора.
Найчастіше швидкість процесу V
виражають зміною кількості dNВ
вихідної речовини або її концентрації dCВ
, кількості або концентрації продукту dNП
і dCП
, а також ступені перетворення β
за час dτ:
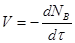   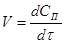 
Є відмінності в характері зміни швидкостей процесів залежно від режиму роботи реактора. У реакторах з періодичним завантаженням нової порції реагентів і відведенням продуктів реакції концентрації реагентів і швидкість процесу зменшуються у міру його здійснення. По довжині безперервно діючого проточного реактора ідеального витискування спостерігається аналогічна залежність. Що стосується реакторів ідеального змішування, то зміни концентрації в них реагуючих речовин і продуктів в часі підтримуються майже постійними від зони завантаження до зони вивантаження маси з апарату (в всьому об’ємі реактору).
Реальний процес хімічних взаємодій є підсумком протікання паралельних і послідовних простих реакцій, кожна з яких йде з швидкістю, яка визначається особливостями умов процесу в системі.
По числу молекул, що беруть участь в елементарному акті хімічного перетворення, розрізняють реакції мономолекулярні, бімолекулярні і тримолекулярні. Оскільки вірогідність одночасного зіткнення трьох молекул мала, тримолекулярні реакції зустрічаються рідко.
Одностороння хімічно зворотня елементарна реакція першого порядку може бути представлена рівнянням
А
→ Продукти реакції
Швидкість реакції першого порядку рівна:
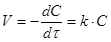 (6) (6)
де k
– коефіцієнт пропорційності (константа швидкості реакції);
C
- поточна концентрація речовини А
.
Інтегруючи рівняння (6), одержимо
 (7) (7)
де C
0
і C
—вихідна і поточна концентрації речовини А.
Рівняння (7) можна представити у вигляді
 (8) (8)
де СХ
— зміна концентрації речовини А
за час τ;
 - ступінь перетворення. - ступінь перетворення.
Якщо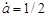 , то , то
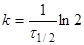 (9) (9)
 (10) (10)
де  —
час напіврозпаду, тобто час, протягом якого прореагує половина речовини. —
час напіврозпаду, тобто час, протягом якого прореагує половина речовини.
Одностороння хімічно зворотня реакція другого порядку схематично може бути представлена рівнянням
А1
+ А2
→ Продукт (продукти) реакції
Швидкість реакції другого порядку дорівнює
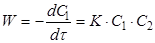 (11) (11)
де С1
і С2
– поточні концентрації А1
і А2
.
Інтегруючи рівняння (11), одержуємо
 (12) (12)
Якщо С1
=С2
=С
, то рівняння (11) прийме вигляд
 (13) (13)
і після інтегрування
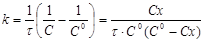 (14) (14)
при С=С0
/2
 (15) (15)
 (16) (16)
Час напівперетворення  для реакції другого порядку обратно пропорційно початкової концентрації реагуючих речовин. для реакції другого порядку обратно пропорційно початкової концентрації реагуючих речовин.
У разі односторонньої реакції п-го
порядку
А1
+ А2
+ А3
+ ... → Продукт (продукти) реакції
 то швидкість реакції дорівнює то швидкість реакції дорівнює
 (17) (17)
Інтегруючи рівняння (17), одержимо
 (18) (18)
Якщо С=С°/2
, то
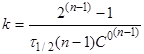 (19) (19)
 (20) (20)
Час напівперетворення реакції п-порядку
обратно пропорційно початковій концентрації реагентів в ступені (п-1).
Порядок реакції визначають, використовуючи дослідні дані про зміну концентрації реагуючих речовин з часом. Якщо в реакції бере участь декілька речовин, необхідно визначити приватні порядки по відношенню до кожної з цих речовин. Існує декілька способів знаходження приватного порядку і порядку реакції.
1.2.4 Кінетична модель топохімічних реакцій
Хімічні перетворення твердих речовин у контакті з газовою або рідкою фазами, а також поліморфні перетворення, що супроводжуються виникненням нової стабільної або метастабільної твердої фази, відносяться до топохімічних. Ці реакції можуть протікати як під дією імпульсів ззовні (термічного, магнітного, звукового, механічного, променевого і т.п.), так і внаслідок реакційної активності взаємодіючих речовин. При цьому тверда фаза, що знов утворюється, може бути стійкою або може розкладатися після деякого індукційного періоду. Прикладами топохімічних реакцій є: випал природної мінеральної сировини; розкладання кристалогідратів і інших подвійних з'єднань; обмінні гетерофазні реакції типу Г-Т
; локальна сокристалізація ізоморфних або "захоплюваних" твердих з'єднань при масовій кристалізації солей з розчинів; поліморфні перетворення кристалічних модифікацій; реакції в системах Т-Т
при дефіциті рідкої фази.
При випалі, розкладанні, обмінній реакції і деяких інших перетвореннях із усією вихідною масою речовини хід процесу інтерполюють у виді графічної залежності ступеня перетворення α
від часу τ
.
Частіше – це криві лінії, що мають S-образну форму (сигмоіда по Дельмону). На початковій ділянці 0 – 1 кривої рис. 1 швидкість перетворення (Δ β/Δτ)1
= β1
/τ1
досить висока (рис. 2.), оскільки перетворення протікає на вихідній поверхні. Потім швидкість перетворення сповільнюється й в індукційному періоді (ділянка 1 – 2 ) воно протікає із середньою швидкістю (Δβ/Δτ)2
= (β2
-β1
)/(τ2
-τ1
).
У період прискорення (ділянка 2 – 3 ) швидкість перетворення найбільша (Δβ/Δτ)3
= (β3
-β2
)/(τ3
-τ2
).
За цим періодом випливає період спаду швидкості перетворення (від значення β у т. 3 до значення β
= 1). Усі ці ділянки одночасно представляються тільки на теоретичному графіку.

Рис.2. Загальний вид зміни ступеня Рис.3. Загальний вид залежності перетворення вихідної речовини від диференціальної швидкості часу перетворення вихідної речовини від часу
На графіках, побудованих по експериментальним даним, звичайно відбивають якісно переважаючі ділянки залежності β
=
f
(τ)
, характерні для основних етапів розвитку топохімічного перетворення. Наявність переважаючої ділянки залежить від питомої поверхні, характеру перетворення, порушень кристалічних структур, співвідношення молярних об’ємів вихідної фази і фази, що утворюється, форми і числа зародків, а також від особливостей швидкості зростання числа ядер зародків від часу.
Багато топохімічних перетворень в неорганічній технології добре описуються емпіричним рівнянням Єрофеєва:
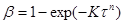 (21)
(21)
де, п
– сума числа послідовних стадій, необхідних для утворення стійкого зародка нової фази, і умовного числа, що відбиває форму цього зародка:
для сферичного – 3,
для циліндричного – 2,
для плоского – 1 [ 1 ].
При побудові графічних залежностей lg [1/(1-β)]
від lg
τ
знаходять К
и п
. У результаті перетворення рівняння (21) одержуємо:
 (22) (22)
Визначаємо кінетичний фактор п
при будь-якому відомому часі τ
з урахуванням обчисленого значення К
и при відповідному ступені перетворення ατ
.
При побудові (рис. 3) графічної залежності (1/n)lg[-ln(1-β)] =
f
(lg τ)
на ось ординат наносять значення lg(1/K), (1/n) lg (1/K)
при lg τ = 0
, потім проводять пряму лінію, тангенс кута нахилу якої дорівнює (1/n).

Рис.4. Графічний метод визначення константи і порядку топохімічної реакції
Для оцінки кінетичних особливостей топохімічних реакцій необхідно виділяти різні їхні стадії, у тому числі утворення і розвитку реакційної поверхні розділу, появи і розподілу деякого числа зародків нової фази, що кристалізується, і так далі.
1.3 Методи розрахунків
1.
3.1 Інтегральні методи розрахунку кінетичних констант
Відшукання констант швидкостей реакцій і перевірка придатності прийнятого рівняння кінетики за допомогою інтегральних методів засновані на використанні інтегральних залежностей, що пов'язують концентрацію реагуючої речовини з параметрами процесу і часом його протікання.
1.3.1.1 Одинична реакція першого порядку
Для процесу з одиничною реакцією першого порядку, швидкість якої виражена через ступінь перетворення
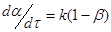 (23) (23)
інтегральна залежність має напівлогарифмічний вигляд
 (24) (24)
Графічно напівлогарифмічне рівняння представляє пряму (рис. 5).
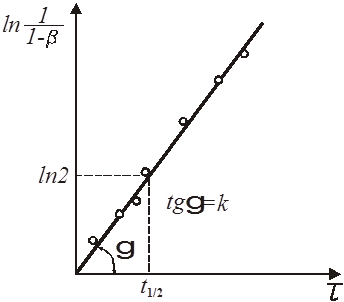
Рис. 5. Напівлогарифмічна залежність ступеня перетворення x
від часу τ для реакції першого порядку
З рівняння і його графіка знаходимо:
 (25) (25)
Якщо досліджувана реакція є дійсно реакцією першого порядку, то обчислене значення k
не повинні змінюватися із збільшенням τ,
і отже, всі точки лежатимуть на прямій.
Для попередньої оцінки величини константи швидкості реакції і придатності прийнятого рівняння можна застосувати простіший спосіб, заснований на використанні часу напівперетворення.
Час напівперетворення визначається як час, протягом якого концентрація реагуючої речовини зменшується на половину своєї первинної величини.
З напівлогарифмічного рівняння реакції першого порядку виходить, що ступінь перетворення досягає величини β=
0,5 у момент часу
 1/2
(26) 1/2
(26)
де τ1/2
– час напівперетворення (рис. 5).
Очевидно, що застосування часу напівперетворення вимагає постановки дослідів при різних температурах, при яких порядок залишався б постійним, а змінювалася б тільки величина k
.
Якщо реакція дійсно першого порядку, то різниця у величинах констант визначатиметься тільки значеннями температури.
Іноді для відшукання константи швидкості реакції першого порядку зручно застосовувати графік експоненціальної кривої (рис.6), використовуючи для цього величину так званого характеристичного часу. Воно визначається як час, необхідне для того, щоб концентрація реагуючої речовини склала від первинної величину в 1/е
разів меншу.

Рис. 6. Експоненціальна крива реакції першого порядку
Дійсно, переходячи від напівлогарифмічного рівняння реакції першого порядку до його експоненціального виразу одержуємо, що в мить, коли час τ досягає величини характеристичного часу t
 (27) (27)
Переходячи від ступеня перетворення до концентрацій, знаходимо:
 (28) (28)
Знаючи відрізок часу, протягом якого концентрація від початку відліку зменшилася в 1/е = 0,369 разу, легко визначити константу швидкості як величину зворотну характеристичному часу:
 (29) (29)
Приклад 1
.
За кінетичними даними, одержаними для реакції
А→ продукти реакції
на досвідченому проточному реакторі було знайдено:
Середній час τ
, сек
|
0,3
|
0,6
|
0,9
|
1,2
|
1,4
|
1,5
|
1,8
|
2,1
|
| Ступінь перетворення β
речовини А
, мол. долі
|
0,167
|
0,363
|
0,474
|
0,57
|
0,63
|
0,66
|
0,716
|
0,79
|
Визначити константу швидкості реакції інтегральним методом, використовуючи графічну побудову напівлогарифмічної залежності і спосіб характеристичного часу.
Рішення. Приймемо, що швидкість реакції підкоряється рівнянню першого порядку. Тоді відповідно до виразу (26) за досвідченими даними будуємо графічну залежність 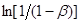 від τ (рис. 7).
від τ (рис. 7).
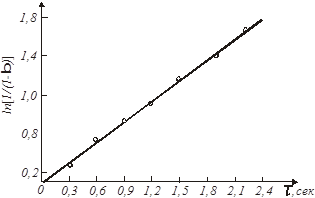
Рис.7. Експериментальна залежність  від часу τ
для реакції А→ продукти реакції
від часу τ
для реакції А→ продукти реакції
Її прямолінійний характер підтверджує правильність зробленого припущення. Тангенс кута нахилу прямої рівний
k
= tgβ = tg 350
/
0,7 с
е
к -1
Згідно рівняння (27), значенню характеристичного часу повинна відповідати величина ступеня перетворення β
= 0,631. За досвідченими даними це значення виходить при τ = 1,4 сек. Отже
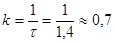 сік -1 сік -1
1.3.1.2 Одинична реакція другого порядку
Розглянемо реакцію з однією реагуючою речовиною. Її рівняння швидкості, виражене через ступінь перетворення, запишеться у вигляді
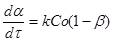 2
(30) 2
(30)
Рішенням рівняння (30) є залежність
 (31) (31)
представлена графічно на рис. 8.

Рис. 8. Залежність ступеня перетворення β
від часу τ для реакції другого порядку з одним реагуючим членом
З нього виходить, що залежність зворотної величини ступеня перетворення або концентрації від часу є пряма, нахил якої дорівнює константі швидкості реакції.
Можна уникнути побудови графіка і просто обчислити значеннями k
з рівняння
 (32) (32)
у різні моменти часу. Якщо реакція протікає по другому порядку, то значення k
,
знайдене з рівняння (31), не повинно мінятися в часі, і тоді за величину константи швидкості реакції можна прийняти її середнє значення.
Для орієнтовної оцінки константи її значення можна визначити, виходячи з часу напівперетворення. Згідно залежності (30), при β
= 0,5 знаходимо:
τ = t1/2
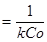 (33)
(33)
Отже, у протилежність реакції першого порядку, тут час напівперетворення залежить від вихідної концентрації реагуючої речовини. Такий результат завжди указує на те, що має місце реакція другого порядку.
Використання інтегральних залежностей для визначення констант швидкостей реакції другого порядку з двома реагуючими речовинами застосовується вельми рідко. Це пояснюється як складністю одержуваних рівнянь і, відповідно їх графічної інтерпретації, так і можливими помилками у разі сумірних по величині вихідних концентрацій реагуючих речовин. Вказані обмеження ще більшою мірою відносяться до реакцій третього порядку, особливо коли в реакції беруть участь дві або три речовини.
Приклад 2.
За кінетичними даними, одержаними для реакції
А → продукти реакції
На експериментальному проточному реакторі було знайдено:
| Середній
час τ, год.
|
0,1
|
0,2
|
0,4
|
0,8
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
| Ступінь перетворення β
речовини А
, мол. долі
|
0,224
|
0,366
|
0,538
|
0,675
|
0,775
|
0,822
|
0,851
|
0,875
|
0,89
|
Початкова концентрація вихідної речовини А С0
= 2 кмоль/м3 .
Визначити константу швидкості реакції.
Рішення. Приймемо, що швидкість реакції підкоряється рівнянню другого порядку. Відповідно до виразу (31) за досвідченими даними обчислюємо значення ординати  і наносимо їх на графік (рис. 9). і наносимо їх на графік (рис. 9).

Рис.9. Експериментальна залежність  від часу τ від часу τ
для реакції А → продукти реакції
Прямолінійний характер залежності підтверджує правильність вибору кінетичного рівняння.
Тангенс кута нахилу прямої дорівнює
k
= tg γ = tg 550 = 1,44 м3
/(кмоль*год.)
Таке ж значення константи виходить і при розрахунку її як середньої величини з урахуванням формули (32)
kср
= 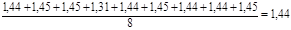 , м3
/(кмоль*год)
, м3
/(кмоль*год)
1.3.1.3 Одинична реакція n-го порядку
Для реакцій n-го порядку визначення кінетичних констант безпосередньо з виразів, що одержуються при інтеграції рівняння швидкості, не представляється можливим. Оскільки ці вирази є трансцендентними і в загальному вигляді щодо константи швидкості реакції і порядку не розв'язуються. Проте у багатьох випадках, використовуючи штучні прийоми (підстановки і графічні залежності), можна обійти утруднення, зв'язані з транцендентністю інтегральної залежності і одержати вирази, в яких порядок і константа швидкості реакції явно залежать від концентрації реагуючих речовин і часу реакції. Деякі з інтегральних методів, що використовують штучні прийоми, викладені нижче.
Метод Эмануэля-Кнорре. Припустимо, що реакція n-
ого порядку описується кінетичною залежністю
 (34) (34)
Інтегруючи цей вираз з вихідними умовами при τ
= 0, β
= 0 приводить до виразу
 (35) (35)
Для відшукання k
і n
досить мати два значення β
: β1
і β2
, відповідні яким-небудь двом моментам часу τ1
і τ2
. Тоді
 ; ; 
Розділивши одну рівність на іншу, одержимо:
 (36) (36)
Рівняння (36) трансцендентне і в загальному вигляді не розв'язується. Проте якщо в діапазоні зміни β
вибрати такі два значення β1
і β2
, щоб виконувалася рівність
 (37) то при (37) то при
 (38) і, отже (38) і, отже
 (39) (39)
рівняння (36) після деяких перетворень приводить до вигляду
 (40) (40)
Підставивши цей вираз для z
в рівняння (38) і потім про логарифмувавши, одержимо рівняння для визначення порядку:
 (41) (41)
По рівнянню (41) при різних β
і τ обчислюються значення n
і визначається їх середньоарифметична величина. Потім з рівняння (35) при знайденому середньоарифметичному значенні n
і величинах β1
, τ1
, β2
, τ2
, і т.д. визначаються значення k
при різних температурах і обчислюються енергія активації перед експоненціальний множник.
Приклад 3.
За даними кінетичних кривих 1-3 (рис.9) визначити в рівнянні швидкості реакції

Порядок реакції n
по і величину константи швидкості реакції k
. Значення 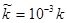 . .
Рішення. З рівняння швидкості реакції після розділення змінних і інтеграції одержуємо:

Підставивши в це рівняння замість x
значення x1
і x 2
, одержимо дві рівність. Розділивши які одне на інше, з урахуванням виразів (38) і (39) знаходимо:
 , ,
де індексами 1 і 2
при  і β
2
позначені номери крапок для значень x1
і x2
на досвідченій кінетичній кривій. і β
2
позначені номери крапок для значень x1
і x2
на досвідченій кінетичній кривій.
Логарифмуючи рівняння (38) і потім вирішуючи щодо n
, маємо:


Рис. 10. Кінетичні криві залежності ступеня перетворення β (мол. долі) від середнього часу перебування  (год.) для реакції (год.) для реакції
1 – розчинення Fe2
O3
в нітратній кислоті;
2 - розчинення NiO в нітратній кислоті;
3 - розчинення CuO в нітратній кислоті.
Вибираємо на кінетичній кривій, наприклад кривою 2, точку з координатами α1
=0,65 і  1
= =0,295.
З умови (37) знаходимо α2
= 0,88. Цьому значенню відповідає 1
= =0,295.
З умови (37) знаходимо α2
= 0,88. Цьому значенню відповідає 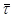 2
= 0,52. За експериментальними даними значення β
2
при швидкостях потоку рідкої фази, відповідних часу перебування 1 і 2, рівні: β21
=0,44 і β22
=0,37; концентрація розчиненого водню С20
=0,18 кмоль/м3
. 2
= 0,52. За експериментальними даними значення β
2
при швидкостях потоку рідкої фази, відповідних часу перебування 1 і 2, рівні: β21
=0,44 і β22
=0,37; концентрація розчиненого водню С20
=0,18 кмоль/м3
.
По рівнянню для z-1
знаходимо:
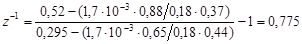
Підставляючи значення x1
і z
в рівність для n
, одержуємо:

Аналогічно визначаємо значення n
при інших α і 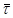 на всьому протязі досвідчених кінетичних кривих. Набутого значення n
приведене нижче: на всьому протязі досвідчених кінетичних кривих. Набутого значення n
приведене нижче:
0,78...........для кривої 1
0,757; 0,90; 1,10......для кривої 2
0,50;0,64; 0,82 ........для кривої 3
Спостережуваний розкид у величинах n
від 0,5 до 1,1 пов'язаний з погрішностями у визначенні x
і  по кінетичній кривій, особливо на ділянках з малою кривизною. по кінетичній кривій, особливо на ділянках з малою кривизною.
Розрахована по знайдених значеннях n
його середня арифметична величина з точністю до десятих рівна 0,8.
Вирішуючи рівняння швидкості реакції щодо константи k
при n
= 0,8 і величинах α1
, τ1
, α2
, τ2
. знаходимо її значення при різних температурах і потім визначаємо величини енергії активації і перед експоненціального множника:
Е = 10000 кал/моль; 
При цих значеннях 
1.3.1.4 Метод графічної інтеграції
У тих випадках, коли вибране рівняння швидкості реакції n-го
порядку аналітично не інтегрується, для визначення константи швидкості реакції можна застосувати графічну інтеграцію. Для цього необхідно від диференціального рівняння швидкості реакції перейти до рівняння в інтегральному вигляді. Для одиничних реакцій це робиться вельми просто. Так, якщо швидкість реакції описується рівнянням вигляду
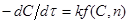 або або
То після розділення змінних і інтеграції маємо:
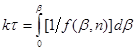 (42) (42)
Задаючись значенням порядку n
, будуємо для підінтегрального виразу в рівнянні (42) графічну залежність (рис. 11), відкладаючи на осі абсцис значення β
, а на осі ординат відповідні їм значення 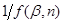 . У плавну криву цієї залежності вписуємо ступінчасту криву, вибираючи сходинки такої ширини, щоб площа під кожною з них була близька до площі під відрізком плавної кривої. Замінюючи інтеграл в рівнянні (42) сумою площ прямокутників під ступінчастою кривою і ділячи величину цієї суми на τ, знаходимо значення константи швидкості реакції k
. Очевидно, що якщо величина порядку n
вибрана вірно, то значення k
, знайдені за площами кожного з прямокутників, повинні трохи відрізнятися від значення k
, знайденого або за сумарною площею, або як середнє арифметичне від значень до для площ прямокутників. Інакше необхідно задати інші значення порядку n
і весь розрахунок повторити наново. . У плавну криву цієї залежності вписуємо ступінчасту криву, вибираючи сходинки такої ширини, щоб площа під кожною з них була близька до площі під відрізком плавної кривої. Замінюючи інтеграл в рівнянні (42) сумою площ прямокутників під ступінчастою кривою і ділячи величину цієї суми на τ, знаходимо значення константи швидкості реакції k
. Очевидно, що якщо величина порядку n
вибрана вірно, то значення k
, знайдені за площами кожного з прямокутників, повинні трохи відрізнятися від значення k
, знайденого або за сумарною площею, або як середнє арифметичне від значень до для площ прямокутників. Інакше необхідно задати інші значення порядку n
і весь розрахунок повторити наново.

Рис. 11. Графічна інтеграція
1.3.1.5 Метод постійних частин
Згідно цього методу, для одиничної реакції, швидкість якої описується рівнянням
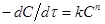 (43) (43)
Експериментальна кінетична крива на всьому своєму протязі розбивається на відрізки такої величини, щоб частка 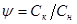 , що є відношенням кінцевого значення ординати відрізка Ск
до вихідного значення Сн
, залишаючись для всіх відрізків постійної. При цьому залежно від величини частки, вибираної абсолютно довільно, відрізки кривої або слідують один за іншим так, що кінець одного є початком іншого, або частково накладаються один на одного. , що є відношенням кінцевого значення ординати відрізка Ск
до вихідного значення Сн
, залишаючись для всіх відрізків постійної. При цьому залежно від величини частки, вибираної абсолютно довільно, відрізки кривої або слідують один за іншим так, що кінець одного є початком іншого, або частково накладаються один на одного.
Розглядаючи значення відрізків Сн
– Ск
= Сн
- Снψ
і відповідним їм значенням відрізків часу τн
- τк
як межі інтеграції рівняння швидкості

одержуємо:
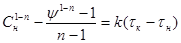 . .
Логарифмуючи це рівняння, знаходимо:
 (44) (44)
Неважко бачити, що одержане рівняння прямої лінії в координатах: ln (τк
– τн
)
– ордината, ln Cн
– абсциса. Одержавши цю пряму при довільно обраному відношенні ψ
і визначивши з графіка 1-n
і  можна розрахувати k
і n.
Для більшої точності розрахунок можна повторити при інших значеннях ψ
. можна розрахувати k
і n.
Для більшої точності розрахунок можна повторити при інших значеннях ψ
.
Приклад 4.
Застосовуючи метод постійних частин, визначити порядок і константу швидкості одиничної реакції. Значення кінетичних параметрів Сн
, τн
, τк
і відповідні їм величини логарифмів при ψ
= 0,5 і 0,9 приведені в таблиці 1.
Таблиця 1. Значення кінетичних параметрів
| ψ
|
τн
|
τк
|
Cп
|
Ск
|
ln Cп
|
(τк
– τп
)
|
ln (τк
–τп
)
|
| 0,5
|
0,00
|
10,0
|
10,0
|
5,0
|
2,30
|
10,0
|
2,30
|
| 0,5
|
1,11
|
12,2
|
9,0
|
4,5
|
2,20
|
11,1
|
2,41
|
| 0,5
|
2,50
|
15,0
|
8,0
|
4,0
|
2,08
|
12,5
|
2,53
|
| 0,5
|
4,30
|
18,6
|
7,0
|
3,5
|
1,95
|
14,3
|
2,66
|
| 0,5
|
6,,66
|
23,3
|
6,0
|
3,0
|
1,79
|
16,6
|
2,81
|
| 0,5
|
10,0
|
30,0
|
5,0
|
2,5
|
1,61
|
20,0
|
3,0
|
| 0,9
|
0,00
|
1,11
|
10,0
|
9,0
|
2,30
|
1,11
|
0,104
|
| 0,9
|
1,11
|
2,35
|
9,0
|
8,1
|
2,20
|
1,24
|
0,215
|
| 0,9
|
2,35
|
3,73
|
8,1
|
7,29
|
2,09
|
1,38
|
0,322
|
| 0,9
|
3,73
|
5,23
|
7,29
|
6,56
|
1,99
|
1,50
|
0,406
|
| 0,9
|
5,23
|
6,92
|
6,56
|
5,91
|
1,88
|
1,69
|
0,525
|
| 0,9
|
6,92
|
8,80
|
5,91
|
5,32
|
1,78
|
1,88
|
0,632
|

а б
Рис. 12. Визначення порядку реакції методом постійних частин:
а - ψ = 0,5; б - ψ = 0,9.
Рішення. Наносимо на графік (рис.12) точки, відповідно табличним значенням ln (τк
– τн
)
і ln Cн
. Через ці точки проводимо пряму і визначаємо кут її нахилу. Як при ψ = 0,5
, так і при ψ = 0,9
, γ = -450
. Тангенс цього кута tg (-450
) = 1-n = -1
. Звідки n=2.
Знаходимо значення відрізків , що відсікаються на осі ординат: , що відсікаються на осі ординат:
для ψ = 0,5
 = 3,05 = 3,05
для ψ = 0,9
 = 0,72. = 0,72.
Вирішуючи цю рівність відносно k
, при n=2
у обох випадках одержуємо k
=0,05.
1.3.2
Оцінка застосовності теоретичних рівнянь
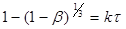 (45)
(45)
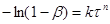 (46) (46)
 (47) (47)
де, k
– константа швидкості, що залежить від температури;
n
– константа, що залежить від присутності в тілі початкових центрів реакції при τ = 0, від форми ядер, числа проміжних стадій у процесі утворення початкових центрів і від деяких інших факторів; вона може мінятися до будь-якого цілого числа.
Рівняння (45) виведено виходячи з припущення, що топохімічна реакція, тобто реакція між газом і твердою речовиною, визначається просуванням фронту ядер твердого продукту реакції усередину зерна з обліком того, що поверхня пропорційна обсягу в ступені 2/3.
Рівняння (46) виведено в припущенні, що процес виникнення початкових центрів (ядер) реакції може бути багатостадійним, тобто що швидкість цього виникнення може залежати від часу (оскільки концентрація реагуючої речовини не залишається постійної в часі).
Рівняння (47) виведено для процесу, що лімітуеться швидкістю внутрішньої дифузії, k
у ньому може бути замінена на вираження:
k
²/ R²
,
де, R
– радіус частки твердої речовини.
Далі будують графіки, що відповідають рівнянням 45; 46; 47.

Рис.12. Обробка даних за рівнянням (45)
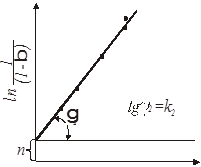
Рис.13. Обробка даних за рівнянням (46)

Рис.14. Обробка даних за рівнянням (47)
Такі залежності будують для кожної дослідженої температури.
Для висновків про застосовність того чи іншого рівняння слід провести статистичну обробку даних, для цього необхідно розрахувати середнє квадратичне виділення або (та) коефіцієнт кореляції.
Незмінність і невеликі відхилення величини К
свідчать про задовільний опис процесу відповідним кінетичним рівнянням.
Більш точні результати виходять при обробці даних на ЕОМ. За розрахунковим значенням β
,
будують криві β =
φ
(
τ
).
Розрахункова – пунктирна лінія, а експериментальна – суцільна.
1.3.3 Розрахунок енергії активації
Енергію активації Е
можна визначити двома способами:
1) за графіком β
=φ (τ)
2) по одній із залежностей, зображених на рис. 12; 13; 14.
Відповідно до останнього способу визначають константи швидкості k
1
и k
2
як тангенси кутів нахилу прямих (див. рис.12), що відповідають температурам, наприклад τ1
і τ2
. Число пар τ
і k
повинно бути не менш чотирьох. По них будують пряму в координатах ln
k
= φ(1/Т)
, відповідній логарифмічній формі рівняння Арреніуса:
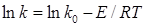 (48) (48)
Розрахунок Е
проводять по формулі:
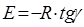 (49)
(49)
де, R
= 8.314 * 10-3
кДж/моль.

Рис.15. Графік для визначення Е
і k
0
Відрізок, що відтинається на осі ln
k
, дорівнює ln
k
0
. Підставляючи отримані дані в рівняння (45) одержують рівняння для конкретної залежності k
=φ (τ).
Орієнтовано величину Е
можна знайти безпосередньо з графіка β = φ (τ)
. Для цього знаходять значення β
для різних температур, що відповідають тому самому часу τк
Потім складають таблицю 2.
Таблиця 2. Дані для визначення Е
по залежності β = φ (τ)
| τ, хв.
|
Т, 0
С
|
βі
|
Відносна величина Квідн.

|
| |
|
|
|
В останню графу заноситься константа швидкості, отримана як результат розподілу кожної величини β
i
на максимальне значення β
max
(відповідне максимальній температурі). За отриманим значенням Квідн
будують графік, аналогічний показаному на рис. 15 і розраховують Е
и k
0.
Коефіцієнт Вант-Гоффа знаходять за формулою:
 (50)
(50)
На основі отриманих результатів роблять висновок про тип і модель кінетики.
2. ПРАКТИЧНА ЧАСТИНА
2.1 Постановка завдання
На підставі експериментальних даних процесу вилучення з'єднань натрію з відпрацьованого никель-хромового каталізатора побудувати кінетичні криві, розрахувати енергію активації, підібрати рівняння, що характеризує кінетику перетворення і підібрати модель процесу.
| Час розчинення τ, хвил.
|
Ступінь вилучення при температурі 200
С, д.о.
|
Ступінь вилучення при температурі 550
С, д.о.
|
Ступінь вилучення при температурі 85 0
С, д.о.
|
| 10
|
0,23
|
0,34
|
0,67
|
| 20
|
0,37
|
0,69
|
0,84
|
| 30
|
0,63
|
0,83
|
0,97
|
| 40
|
0,80
|
0,91
|
0,99
|
| 50
|
0,92
|
0,94
|
1,00
|
| 80
|
1,00
|
1,00
|
1,00
|
2.2 Виконання завдання
За даними таблиці будуємо кінетичні криві для заданих температур 1 - 20 0
С, 2 - 55 0
С і 3 - 85 0
С відповідно (рис. 16).

Рис. 16. Кінетичні криві
На підставі графічних залежностей ступеню перетворення початкової речовини від часу τ
(рис. 16) визначаємо швидкість процесу:

де k
– відносна швидкість реакції, хвил-1
.
По тангенсу кута нахилу прямих (рис. 16) визначаємо константу швидкості екстракції натрію з каталізатора: k20
= 0,02; k55
= 0,045; k85
= 0,11 [хвил -1
].
Для кінетичної обробки даних складаємо таблицю:
| 
|

|
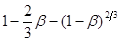
|
| 20 0
С
|
55 0
С
|
85 0
С
|
20 0
С
|
55 0
С
|
85 0
С
|
20 0
С
|
55 0
С
|
85 0
С
|
| 1,08
|
0,36
|
0,26
|
0,3
|
0,11
|
0,08
|
0,073
|
0,015
|
0,01
|
| 1,83
|
1,17
|
0,46
|
0,46
|
0,32
|
0,083
|
0,14
|
0,08
|
0,015
|
| 3,5
|
1,77
|
0,99
|
0,69
|
0,44
|
0,28
|
0,25
|
0,14
|
0,065
|
| 4,6
|
2,35
|
1,61
|
0,78
|
0,54
|
0,41
|
0,29
|
0,19
|
0,13
|
За даними таблиці будуємо графіки, які відповідають кінетичним рівнянням 45, 46, 47 (рис. 17-19).
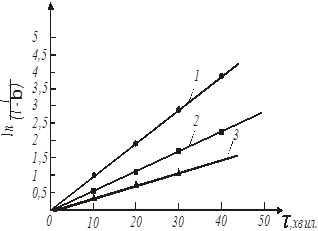
Рис. 17. Обробка даних по рівнянню 45
(1 – температура 20 0
С, 2 - температура 55 0
С, 3 - температура 85 0
С).

Рис. 18. Обробка даних по рівнянню 46
(1 – температура 20 0
С, 2 - температура 55 0
С, 3 - температура 85 0
С).
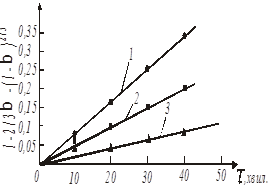
Рис. 19. Обробка даних по рівнянню 47
(1 – температура 20 0
С, 2 - температура 55 0
С, 3 - температура 85 0
С).
Вплив температури на константу швидкості процесу описується рівнянням:
 (51) (51)
 (48) (48)
Для визначення енергії активації будуємо графічну залежність lnk
від 1/Т (рис.17).
Т
, 0С
Т, К 1/T
20 293 3,41•10-3
55 328 3,05•10-3
85 358 2,79•10-3
ln k20
= ln
0,02= -3,91 ln k55
= ln
0,045= -3,1 ln k85
= ln
0,11= -2,21

Рис. 20. Залежність ln
k
від 1/T
Графічна залежність ln
k
= f(1/T)
(мал. 20) дозволяє визначити чисельне значення ln k0
енергії активації по формулі 49:
 (52) (52)
Розрахункове значення енергії активації складає 21,5 кДж/моль, а чисельне значення ln k0
= = -5,6 . В результаті, відповідно до рівняння 48, вплив температури на константу швидкості екстракції водорозчинних домішок з каталізатора описуватиметься рівнянням:
 (53) (53)
а сам процес екстракції домішок відповідно до виразів 48,49,51 рівнянням:
 (54) (54)
де βτ
– поточний ступінь вилучення натрію;
Т
– температура процесу, К;
τ– час, хвил.
ВИСНОВОК
Процеси вилужування протікають в кінетичній області мають енергію активації 40 - 300 кДж/моль, а в дифузійній 8 - 21 кДж/моль. На підставі цього можна зробити висновок, що процес екстракції натрію з никель-хромового каталізатора лежить в дифузійній області. Враховуючи, що домішки, внесені в каталізатор в процесі експлуатації, знаходяться в тонкому його зовнішньому шарі і не проникли глибоко в пори, лімітуючою стадією слід вважати дифузію іонів в прилеглому до каталізатора шарі води.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Панченков Г.М., Лебедев В.П. Химическая кинетика и катализ: Учеб. пособие для вузов. Изд. 3-е перераб. и дополн. – М.: Химия, 1985.-592 с.
2. Позин М.Е., Зинюк Р.Ю. Физико-химические основы неорганической технологии: Учеб. пособие для вузов. – Л.: Химия. 1985.-384 с.
3. Безденежных А.А. Инженерные методы составления уравнений скоростей реакций и расчета кинетических констант. – Л.: Химия, 1973.-256с.
4. Царева З.М., Орлова Е.И. Теоретические основы химической технологии. – к.: Вища шк., 1986.-271 с.
5. Зайцев О.С. Общая химия. Состояние веществ и химическое реакции. – М.: Химия. 1990.-352 с.
6. Романенко Н.В., Орлов А.Г., Никитина Г.В. Книга для начинающего исследователя- химика – Л.: Химия, 1987. – 280 с.
7. Розовский А.Я. Кинетика топохимических реакций – М.: Химия, 1974. – 274 с.
8. Курса Н.Є., Корчуганова О.М. Методичні вказівки для виконання лабораторної роботи з УНДР "Термоваговий аналіз при постійній температурі" (для студентів спеціальності 7.091602 "Хімічна технологія неорганічних речовин" очної і заочної форм навчання ) – Сєвєродонецьк: СТІ СНУ ім. Володимира Даля. 2005 – 19 с.
10. Соловьёв Г.И., Суворин А.В., Колесникова Т.Б. Методические указания к выполнению контрольных заданий по дисциплине "Кинетика и катализ в ТНВ" (для студентов заочной формы обучения специальности "Химическая технология неорганических веществ") – Северодонецк: изд-во СТИ, 2005 г., 75 стр.
|