Лабораторная работа: Обеспечение надежности энергосистемы

Государственное образовательное учреждение

высшего профессионального образования

«Томский Политехнический Университет»

Отчет по лабораторной работе №1

Обеспечение надежности энергосистемы

Выполнил студент

Патенко М.С.

Томск - 2010

Перед нами стоит инженерная задача. Правильное” решение задачи инженерного анализа “правильным” методом возможно лишь при учете ограничений, с которыми сталкивается инженер, решающий эту задачу. Задача, сведенная к конкретному вопросу, позволяет выразить получаемое решение через величины, которые можно затем вычислить или измерить. Другими словами, нужно ставить такой вопрос, на который можно получить количественный ответ. Модель представляет собой идеализированное приближение к реальной ситуации. Построение хорошей аналитической модели предполагает принятие допущений, учитывающих относительную важность различных элементов задачи. Применение физических принципов и накопление данных. После построения аналитической модели можно воспользоваться знаниями и методами научных и технических дисциплин. Для выполнения любой инженерной задачи необходимо определить основную цель, которую необходимо достичь, т.е. нужно четко определиться для чего мы собираемся выполнять те или иные действия. И каков будет результат (что мы будем иметь) при достижении поставленной цели. Будет ли в конечном итоге достигнутая цель удовлетворять решению поставленной задачи. Поэтому выполняемую лабораторную работу можно разделить на три основных этапа определение цели, ход работы, анализ и вывод. Которые в свою очередь подразделяются на подэтапы.

Определение цели

Основной задачей в нашей работе является выбор технического резерва генерирующих мощностей в электроэнергетической системе с учетом проведения планово-предупредительных ремонтов генераторов.

Для бесперебойного снабжения потребителей электроэнергией требуемого качества, суммарный уровень мощности генерирующих агрегатов должен быть не менеепрогнозируемого максимума нагрузки. При равенстве указанных мощностей любое снижение располагаемой мощности или увеличение нагрузки приводит к дефициту мощности и недоотпуску электроэнергии потребителям. Дефицитом называют превышение запроса мощности над располагаемой мощностью ЭЭС. При отсутствии резерва генерирующих мощностей прибегают к восстановлению баланса активной мощности в ЭЭС путем принудительного уменьшения нагрузки за счет отключения наименее ответственных потребителей. Случайные отклонения генерируемой или потребляемой мощностей происходят на практике очень часто. Для снижения возможного недоотпуска электроэнергии потребителям и обусловленного им экономического ущерба принято в энергосистеме создавать резерв генерирующих мощностей, т.е. некоторое превышение располагаемой мощности над прогнозируемым максимумом нагрузки. При определении резерва необходимо учесть проведение ежегодных планово-предупредительных ремонтов, вызывающих заранее планируемые простои генераторов.

Основными признаками, в соответствии с которыми осуществляется классификация составляющих резерва генерирующей мощности, являются их функциональное назначение и мобильность – время от момента возникновения потребности в резерве до момента полного использования резерва для покрытия потребности. В общем случае резерв генерирующей мощности классифицируют с точки зрения энергетической обеспеченности и в зависимости от зоны действия. По функциональному назначению резерв генерирующей мощности разделяется на две арифметически суммируемые составляющие: ремонтный резерв и оперативный резерв. Ремонтный резерв предназначается для компенсации снижения располагаемой мощности системы, вызываемого выводом генерирующего оборудования в предупредительный или плановый ремонт. Оперативный резерв предназначается для компенсации небаланса между генерированием и потреблением мощности, вызванного отказами элементов (оборудования), непредвиденным увеличением нагрузки. Поэтому при возникновении небалансов мощности оперативный резерв в свою очередь делят на аварийный и нагрузочный. Аварийный резерв служит для компенсации снижения располагаемой мощности системы, вызванного частичными или полными отказами элементов (оборудования). Нагрузочный резерв служит для компенсации покрытия непредвиденного увеличения нагрузки, включая ее случайные колебания. Все перечисленные виды резерва могут быть объединены под названием технического резерва энергетической системы.

Задача решается исходя из требований к надежности ЭЭС, определенной нормативными значениями коэффициента готовности системы (³ 0,999) и коэффициента бездефицитной работы (³ 0.996).

Полагаем ЭЭС концентрированной инеоднороднойсистемой. Концентрированной энергосистемой считаем такую, в которой связи между отдельными узлами не накладывают ограничений на потоки мощности в нормальных и аварийных режимах работы. Под неоднороднойсистемой понимаем систему, содержащую несколько групп разнотипных генераторов.

Расчетным периодом является 1 год.

Порядок расчета режимной надежности представлен логической блок-схемой (рис.1)

Исходя из вышесказанного, рассмотрим первый блок - Подготовка исходных данных: а) построение моделей зимних и летних нагрузок; б) построение годовой модели. Данные модели нам необходимы для определения грачиного варианта бездефицитной работы ЭЭС.После применения теории задача сводится к нахождению числовых результатов.

· Исходные данные

· Параметры генераторов

Рис.1 Логическая схема определения потребности ЭС в резерве генерирующей мощности.

режимная надежность генератор электроэнергетический

Таблица 2.2- Нагрузка в относительных единицах

Продолжительности периодов годового графика нагрузки

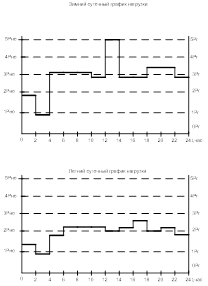
Проанализировав полученные модели можно сделать вывод, что при аварийном или плановом отключении даже одного генератора в зимний период неизбежно нарушение энергообеспечения потребителя на интервале от 2 до 4 часов. Построив годовую модель возможно определение распределения нагрузок в течение всего года.

Исходя из годовой модели нагрузок мы можем определить вероятность появления каждой нагрузки в указанный период. Что позволит перейти ко второму блоку логической схемы.

Определение вероятностей нагрузки и генерации.

Определив вероятность возникновения нагрузок и генерации мы сможем выстроить вероятностную модель соответствия генерируемой мощности требуемым нагрузкам.

Вероятность существования нагрузки в течение расчетного периода

Р, кВт	t, час	Вероятность появления нагрузки
135	548	0,062557078
94,5	1096	0,125114155
87,75	1644	0,187671233
81	2192	0,250228311
74,25	182	0,020776256
67,5	910	0,103881279
60,75	364	0,041552511
54	912	0,104109589
40,5	182	0,020776256
27	730	0,083333333
135	548	0,062557078
94,5	1096	0,125114155
итого	1

Определение вероятности существования нагрузки в течение расчетного периода.

Вероятность существования нагрузки в течение расчетного периодаопределяется как отношение (длительности потребления мощности ) к продолжительности расчетного периода T0 (24 часа – для суточного графика нагрузки, 12 месяцев или 8760 часов – для годового), т.е.

,

где i – номер интервала; N – количество интервалов, соответствующих количеству разных ступеней графика нагрузок; - суммарная длительность нагрузки с уровнем за сутки.

Определение биноминальных коэффициентов и коэффициентов готовности групп однотипных генераторов.

Ряд распределения для i-й группы имеет вид многочлена

(6)

где ni – количество агрегатов в i -й группе;

mi – отключенные агрегаты в i -й группе;

(ni-mi) – находящиеся в работе агрегатыi -й группы;

Pгi – номинальная мощность агрегатов i -й группы;

– коэффициент (вероятность) работы генераторов i -й группы с мощностью .

Генерируемая мощность – случайная величина с биномиальной функцией распределения. Для расчета коэффициентов используем формулу биноминального распределения:

, (7)

где – биномиальный коэффициент;

– коэффициент вынужденного простоя mi генераторов (справочная величина);

– коэффициент готовности генераторов i-й группы.

Определим биноминальный коэффициентдля каждой группы генераторов по формуле:

, (8)

Далее по известным коэффициенту вынужденного простоя mi генераторов и коэффициенту готовности генераторов i-й группы в степени определим коэффициент готовности генераторов мощностью. Для этого воспользуемся формулой (6).

Таким образом мы определили вероятность совпадения вырабатываемой мощности обеими группами генераторов.

Третий блок – формирование вероятностной модели ЭЭС

Совпадение процессов производства и потребления во времени выразим через вероятностные модели этих процессов полученные в предыдущем блоке логической схемы.

Данная модель точно показывает при каких сочетаниях нагрузки и генерации возникает дефицит, а при каких профицит. Заметим что бездефицитное состояние показывает положительное значение. Такое представление модели приблизит ее к практически важной оценки недоотпуска электроэнергии вследствие возникновения дефицитных состояний.

Блоки: определение коэффициента бездефицитной работы и индекса надежности.

Коэффициент бездефицитной работы определяется по вероятностной модели функционирования ЭЭС полученной путем вычленения состояний энергосистемы, в которых дефицит не возникает, т.е. при , и суммирования вероятностей возникновения этих состояний:

где - уровни располагаемой мощности энергосистемы, в составе которой G генераторов на интервале i = 0,G ; - ступени пронумерованной на интервале j = 1, N нагрузки в соответствие с графиком нагрузки.

Определение коэффициента готовности ЭС.

Коэффициент готовности определим по формуле:

К_г = ( Э – DЭ)/Э,

где Э – годовая потребность в электроэнергии; DЭ – математическое ожидание недоотпуска электроэнергии за год вследствие дефицита мощности.

Коэффициенты мощности, для которых не выполняется условие , называют коэффициентами дефицитной работы системы. Математическое ожидание недоотпуска электроэнергии за год вследствие дефицита мощности в энергосистеме определится по формуле:.

,

где - коэффициент ряда распределения дефицитных состояний, соответствующий уровню дефицита Р_{Д i} ; 8760 – количество часов в году.

Проведя необходимые расчеты получаем вероятность бездефицитных состояний К_ДБ =0,997; индекс надежности α=0,9996.

Для оценки резерва мощности используют два определенных ранее показателя:

1. Коэффициент готовности определенный через отношение отпущенной энергосистемой электроэнергии к общей ее потребности:

К_г = ( Э – DЭ)/Э,

Нормативное минимальное значение .

2. Коэффициент бездефицитной работы определенный по вероятностной модели функционирования ЭЭС путем вычленения состояний энергосистемы, в которых дефицит не возникает, и суммирования вероятностей возникновения этих состояний:

Нормативное минимальное значение .

Резерв считается достаточным, если и .

В случае недостаточности резерва, т.е. невыполнения условий и необходимо ввести дополнительные генерирующие мощности и проделать расчет сначала в аналогичной последовательности.

Поскольку полученные нами данные удовлетворяют заданным значениям, то переходим к решению следующего блока – вывод генераторов в ремонт.

Производя расчеты коэффициента К_бд и α, при выведенных генераторах в ремонт получаем результаты не удовлетворяющие нормативным требованиям, поэтому для поддержания должного уровня надежности ЭС и соблюдения нормативных значений коэффициентов К_бд и α при ремонте введем дополнительный резервный генератор на 30 МВт.

После чего производим расчеты нормативных коэффициентов повторно.

Вероятностная модель энергосистемы с учетом выведенных генераторов в ремонт в зимний период.

Вероятностная модель энергосистемы с учетом выведенных генераторов в ремонт в летний период.

Определяем среднее значение недоотпуска электрической энергии в энергосистеме за зимний период

Проведя необходимые расчеты получаем вероятность бездефицитных состояний К_ДБ =0,996; индекс надежности α=0,999.

Поскольку полученные коэффициенты соответствуют нормативным параметрам, то считаем, что уровень надежности производства электроэнергии в ЭЭС является достаточным. Следовательно, можем переходить к следующему блоку нашей логической схемы.

Составление модели ППР

Данная ЭЭС в целом рассчитана по количеству установленных агрегатов и не учитывает того, что часть агрегатов может находиться в плановом ремонте, причем количество таких агрегатов в течение года может изменяться.

Проиллюстрируем определение необходимого технического резерва генерирующих мощностей путем прямого моделирования вывода генераторов в ремонт. Исходной информацией будет служить годовой график месячных максимумов нагрузки ЭЭС с учетом сезонных колебаний.

Основная задача данного блока заключается в соответствии надежности производства электроэнергии в ЭЭС нормативным показателям при условии, что определенное число генераторов будет выведено в ремонт.

Исходя из модели зимних и летних максимумов выводим генераторы мощностью 30 МВт в и генераторы 2ой группы мощностью 25 МВт в летний период т.к. длительность планового ремонта генераторов 1ой и 2ой группы соответствует 0,5 месяца. Что позволит во временном промежутке выполнить ремонты всех генераторов в установленные сроки.

Первоначально выводим генератор 1ой группы в ремонт, следовательно мощность генерируемая наше ЭЭС снизится на мощность соответствующую мощности генератора и на время его планового ремонта. Поэтому определим вероятность бездефицитных состояний и коэффициента надежности для данной модели. Вычисление проводятся аналогично предшествующим моделям. В результате которых получаем значения К_бд =0.996 и α=0,999, что соответствует требуемым нормативам. Далее выводим в ремонт генераторы 2ой группы мощностью 25МВт. Аналогично проведя вычисления получаем К_бд =0.996 и α=0,999.

Полученные значения нормативных коэффициентов позволяют вывести в ремонт каждый из имеющихся генераторов в установленные сроки в течение года, без ущерба надежности производства электроэнергии в ЭЭС. Графическую модель можно изобразить следующим образом.

Анализ и вывод:

Теперь, когда нами получен некоторый числовой результат, его нужно оценить. Кроме того, нужно установить, можно ли сделать обобщения, которые дадут нечто большее, чем просто решение конкретной задачи.

Инженерный анализ был представлен здесь в виде последовательности этапов. Хотя потребовалось многократное решение одной и той же задачи, прежде чем будет получен удовлетворительный результат. Отметим еще раз, что на процесс решения задачи налагаются ограничения, обусловленные такими факторами, как коэффициент готовности и вероятность бездефицитной работы.

В итоге основная задача в нашей работе - выбор технического резерва генерирующих мощностей в электроэнергетической системе с учетом проведения планово-предупредительных ремонтов генераторов была выполнена. Составлен график вывода в ремонт имеющихся мощностей который, позволяет без нарушения надежности производства электроэнергии в ЭЭС и отклонения от нормативных параметров производить ППР. Также была определена надежность изначально заданной ЭЭС и введены недостающие мощности.