Задача 1
Испытываемая жидкость заливается в кольцевую щель на высоту h между цилиндрами А и В (см. рис. 1). Для вращения цилиндра В относительно цилиндра А с частотой n нему должен быть приложен момент М. пренебрегая моментом трения в опорах, определить динамический и кинематический коэффициенты вязкости жидкости с плотностью с. При расчете принять в >> D-d, где в и в – диаметры цилиндров.
| Номер варианта |
M,
H·см
|
n,
об/мин
|
D,
Мм
|
d,
мм
|
h,
мм
|
с,
г/см3
|
| 9 |
1500 |
80 |
208 |
200 |
120 |
0,72 |

Рис. 1
Решение
Возникает момент сопротивления:
dMтр
= 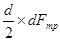 , ,
где 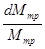 = =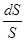 ; S – площадь цилиндра. S= р·d·h. ; S – площадь цилиндра. S= р·d·h.
По закону Ньютона (для внутреннего трения):
dFтр
= 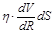 . .
Приближенно находим
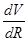 = = . .
где Vнар.
– скорость наружного цилиндра диаметра d; Vвнутр.
= 0 – скорость внутреннего цилиндра диаметра D.
Vнар.
= 2 р·n·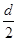 . .
Получаем численно:
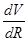 = = 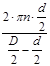 = = 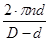 . .
Получаем для нашего случая, сила трения действующая на внутренний цилиндр:
Fтр
= з·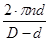 ·S. ·S.
Вращающий момент силы трения:
Mтр
= Fтр
·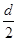 . .
Получаем,
Mтр
= з·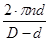 · р·d·h· · р·d·h·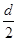 . .
При установившимся движении М = Mтр
:
М = з·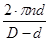 · р·d·h· · р·d·h·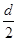 . .
Находим динамический коэффициент вязкости:
з = 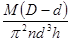 , ,
з =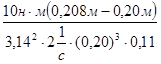 = = 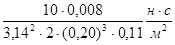 = 4,610 Па·с. = 4,610 Па·с.
Находим кинематическую вязкость жидкости (кинематический коэффициент вязкости жидкости):
д = 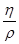 = =  = 6,40·10-3 = 6,40·10-3
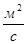 . .
Ответ: динамический коэффициент вязкости – з = 4,978 Па·с; кинематический коэффициент вязкости д = 6,40·10-3
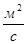 . .
Задача 2
Определить разность давлений в точках А и В, заполненных водой резервуаров (см. рис. 2), если известны показания ртутного дифманометра Д h= 20 см и расстояние между точками Н =0,7 м. Плотность воды св
= 1000 кг/м3
; ртути срт
= 13,544·103
кг/м3
.
вращение цилиндр вязкость давление

Рис. 2
Решение
Давление на уровне О- О можем определить так:
Ро
= РА
+ сВ
g (Н + Дх + Дh),
Ро
= РА
+ сВ
·g·Дх +срт
·g·Дh).
Получаем из полученных выражений:
РА
+ сВ
g (Н + Дh)+ сВ
·g·Дх = сВ
·g·Дх+срт
·g·Дh+РА
– РВ
= срт
·g·Дh– сВ
g (Н + Дh) = 13,544·103
кг/м3
·9,8 м/с2
· 0,2 м – 1000 кг/м3
· 9,8 м/с2
· 0,9 м = 17726,24 Па.
Ответ: разность давлений между точками А и В составляет 17726,24 Па.
Задача 3
Прямоугольное отверстие высотой h= 300 мм и шириной b = 800 мм в вертикальной стенке заполненного водой закрытого резервуара закрыто щитком, вращающимся вокруг горизонтальной оси О (см. рис. 3). Щит прижимается грузом, подвешенным на рычаге длиной r = 1000 мм. Определить минимальный вес груза и построить эпюру давлений на щит, если известны глубина погружения нижней кромки отверстия под водой Н = 1000 мм, расстояние от верхней кромки отверстия до оси вращающегося щита а= 90 мм и показание пружинного манометра со
= 1,1·104
Па. Весом рычага и трением в опоре пренебречь. Плотность воды св
= 1000 кг/м3
. момент инерции прямоугольника относительно центральной оси определяется по формуле J = b·h3
/12.

Рис. 3
Решение
Манометр показывает избыточное давление по отношению к атмосферному.
Сила давления суммарная, действующая на щит с внутренней стороны щита равна:
F = [Po
+ с·g (H-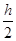 )]·b·h. )]·b·h.
Находим ее приложение (давление рассчитываем для центра тяжести т. площадки). Сила давления не приложена в центре тяжести площадки, т.е. в точке А.
Сила давления в точке В, где АВ = J/b·h·HA
;
НА
= 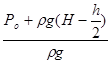 = = 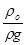 + (H- + (H- 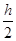 ). ).
Находим минимальный подвешенный груз, чтобы щит не раскрылся:
Q ·Г ≥ F·(a+ 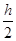 + АВ). + АВ).
Qmin
= 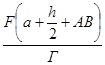 = = 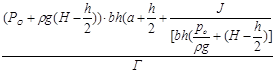 = =
=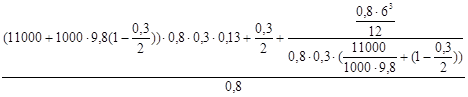 = =
= 3898,69 H
Ответ: минимальный вес груза 3898,69 Н, эпюра давлений на щит показана на рис. 3.
Задача 4
Открытый вертикальный цилиндрический сосуд (рис. 4) радиусом R = 1,2 м с жидкостью равномерно вращается вокруг вертикальной оси со скоростью щ = 80 об/мин. Определить высоту жидкости ho
после остановки сосуда и глубину воронок h2
, если известна высота жидкости h1
= 1,5 м.

Рис. 4
Решение
Скорость вращения:
щ = 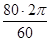 = 8,37 с-1
. = 8,37 с-1
.
Высота параболоида (глубина воронки):
h2
= 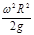 = = 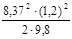 = 5,1 м. = 5,1 м.
Объем параболоида вращения равен:
Vпар
= р·R2
· 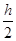 . .
Высота покоящейся жидкости:
ho
= h1
– 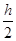 =1,5 – =1,5 – 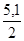 = 1,05 м. = 1,05 м.
Ответ: высота жидкости после остановки сосуда ho
= 1,05 м.
Задача 5
Вода вытекает из резервуара, в котором поддерживается постоянный уровень, через трубопровод при атмосферном давлении в конце трубопровода. Пренебрегая сопротивлениями, определить уровень в резервуаре, расход воды Q и построить напорную и пьезометрическую линию, если известны показания ртутного дифференциального пьезометра h, диаметры трубопроводов D1
= 200 мм, D2
=190 мм, в = 150 мм, плотность ртути и воды соответственно срт
= 13,5 ·103
кг/м3
; св
= 1000 кг/м3
. Атмосферное давление Ра
= 105
Па.

Рис. 5
Решение
Давление статическое в сечении трубки диаметром D1
:
P1
= Pa
+ сgH– 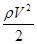 . .
Давление статическое в сечении трубки диаметром d:
P = Pa
+ сgH– 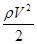 . .
Используя дифференциальный пьезометр, находим:
P1
– P = (срт
– св
) gh,
т.е.  = (срт
– св
) gh(1) = (срт
– св
) gh(1)
при выходе из трубы имеем:
Pa
+ сgH– 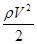 = Pa
(2) = Pa
(2)
Исходя из неразрывности струи, имеем:
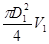 = = 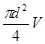 = = 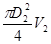 . .
После сокращения получаем:
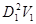 = d2
·V = = d2
·V = 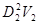 (3). (3).
На основании выражения (3), можем записать:
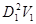 = d2
·V. = d2
·V.
V1
= 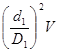 . .
Подставляем полученное выражение в выражение (1), получаем:
V2
-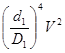 = = 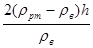 . .
V= 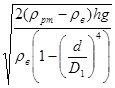 = = 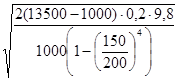 = 71,67 м/с. = 71,67 м/с.
Находим расход воды:
Q = 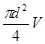 = = 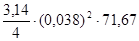 = 0,081240 м3
/с = 81,24 л/с. = 0,081240 м3
/с = 81,24 л/с.
Находим высоту столба воды Н в резервуаре:
сgH = 
gH = 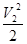 ; H = ; H = 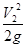 . (атмосферное давление не учитывается). . (атмосферное давление не учитывается).
Из уравнения (3), имеем:
V2
= 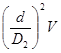 . .
Получаем:
Н = 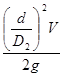 = = 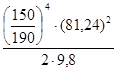 = 130,48 м. = 130,48 м.
Ответ: высота воды в резервуаре Н = 130,48 м; расход воды Q = 81,24 л.
Задача 6
В водопроводной сети имеется участок АВ с тремя параллельными ветвями (см. рис. 6). Определить потерю напора h на этом участке и расходы ветвей Q1
, Q2
, и Q3
, если расход магистрали Q = 110 л/с, диаметры и длины участков D1
= 275 мм; D2
= 175 мм; D3
= 200 мм; l1
= 500 м; l2
= 1100 м; l3
= 1300 м. Трубы нормальные.

Рис. 6
Решение
В соответствии с уравнением неразрывности потока расход жидкости по данному трубопроводу будет:
Q = Q1
+ Q2
+ Q3
(1)
Рассчитаем потери напора в каждом трубопроводе:
Нпот.1
= б1
·Q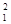 , где Q1
= , где Q1
= 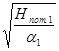 , ,
Нпот.2
= б1
·Q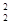 , где Q2
= , где Q2
= 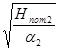 , (3) , (3)
Нпот.3
= б1
·Q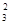 , где Q3
= , где Q3
= 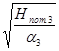 . .
Потери напора в любом из простых трубопроводов, а также общие потери напора в рассматриваемом сложном трубопроводе будут равны разности полных напоров в сечениях А иВ:
НА
– НВ
= Нпот.1
= Нпот.2
= Нпот.2
= Нпот.
(4).
Подставляем в выражение (1) выражение (3) получаем:
Q = 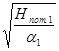 = = 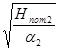 = = 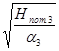 = =  . (5) . (5)
Поскольку местными сопротивлениями можно пренебречь, сопротивления отдельных простых трубопроводов могут быть найдены по одной из формул:
А = Адл
·l; a= 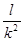 . .
Из формулы (5) имеем:
Нпот
= 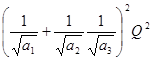 . .
Из таблицы для нормальных труб, имеем:
D1
= 275 мм;  0,613 м6
/с. 0,613 м6
/с.
D2
= 175 мм;  0,212 м6
/с. 0,212 м6
/с.
D3
= 200 мм;  0,116 м6
/с. 0,116 м6
/с.
Находим потери напора по формуле (5):
а1
= 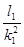 = = 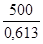 = 815,66 = 815,66
а2
= 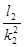 = = 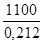 = 5188,67 = 5188,67
а1
= 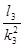 = = 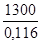 = 11206,89 = 11206,89
Нпот
= 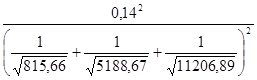 = 6,032 = 6,032
Q1
=  = 0,085 м3
/с = 85 л/с. = 0,085 м3
/с = 85 л/с.
Q2
= 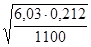 = 0,0340 м3
/с = 34 л/с. = 0,0340 м3
/с = 34 л/с.
Q3
= 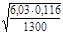 = 0,0231 м3
/с = 23,1 л/с. = 0,0231 м3
/с = 23,1 л/с.
Q1
+ Q2
+ Q3
= 0,14 м3
/с = 142,1 л/с.
Ответ: потеря напора на участке АВ составляет 6,032 м. рт. столба, а расходы Q1
= 85 л, Q2
= 34 л/с; Q3
= 23,1 л/с.
Задача 7
Вода под давлением Po
подводится по трубе диаметром dc
= 13 мм, в котором происходит увеличение скорости и понижение давления (см. рис. 7). Затем в диффузоре поток расширяется до диаметра d= 50 мм. Вода выходит в атмосферу на высоте Н2
= 1,3 м и поднимается из нижнего резервуара на высоту Н1
= 2,5 м. определить минимальное давление Ро
перед эжектором с учетом потерь напора в сопле (ос
= 0,06), диффузоре (одиф
= 0,25), коленах (ок
= 0,25).
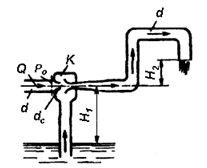
Рис. 7
Решение
Запишем уравнение Бернулли (перед соплом и на выходе):
1) Ро
+ 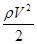 = Ра
+ = Ра
+ 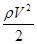 +сg(H1
+ H2
) +(0,06+2·0,25) +сg(H1
+ H2
) +(0,06+2·0,25) 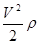 . .
Давление в струе после сопла будет:
2) Рс
£ Ра
– сgH1.
Запишем уравнение Бернулли (перед соплом и после сопла в сечениях):
3) Ро
+ 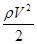 = Ра
– сgH1
+ = Ра
– сgH1
+ 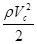 +0,06 +0,06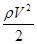 . .
Уравнение неразрывности струи:
4)  = = 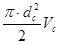 ; d2
V = ; d2
V = 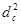 Vc
; Vc
= Vc
; Vc
=  ·V. ·V.
Численная связь Vc
= 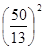 ·V. ·V.
Решаем систему:
Из уравнения (1) отнимаем уравнение (3) и находим
0=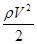 + сg(2H1
+ H2
) + + сg(2H1
+ H2
) + 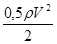 – с – с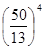 · · 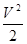 . .
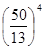 · · 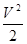 – – 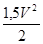 = g(2H1
+ H2
). = g(2H1
+ H2
).
V2
= 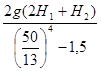 = = 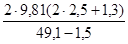 = 0,56 м2
/с2
. = 0,56 м2
/с2
.
Из первого уравнения имеем:
Р0
³ Ра
+ сg(H1
+ H2
) + 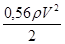 = Ра
+ 1000·9,81 (2,5+1,3) + = Ра
+ 1000·9,81 (2,5+1,3) + 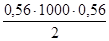 = Ра
+ 37434,8 Па. = Ра
+ 37434,8 Па.
Ответ: минимальное давление перед инжектором Po
= Pa
+ 37434,8 Па.
Литература
1. Р.Р. Чугуев. Гидравлика. М., 1991 г.
2. В.Г. Гейер, В.С. Дулин, А.П. Заря. Гидравлика и гидропривод. М. «Недра», 1991 г.
3. К.Г. Асатур. Гидравлика, конспект лекций, Л., ЛГИ., ч. 1 и 2.
|