Асимптотические методы исследования интегралов с параметром
Курсовая работа
Выполнил: ст-т 4 курса Бутаев Г.Н.
Дагестанский государственный университет
Махачкала 2006
Введение
Многочисленные задачи математики, математической физики,механики,техники приводят к необходимости исследовать интегралы вида
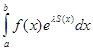
при больших значениях параметра  . .
Можно по пальцам пересчитать те случаи,когда такие интегралы явно вычисляются.
С другой стороны,при больших значениях параметра вычисление значений таких интегралов не под силу даже самым современным ЭВМ.Единственное,что остается – это попытаться воспользоваться асимптотическими методами.
Асимптотические методы, к сожалению, также имеют свои границы. Не следует думать, что асимптотику любого интеграла вышеприведенного вида можно вычислить. Но в ряде случаев получающиеся асимптотические формулы настолько просты,что сомневаться в применении именно этих методов не приходится.
1.Основные формулы
Интегралами Лапласа называются интегралы вида
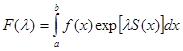 , (1.1) , (1.1)
где 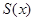 -вещественнозначная функция, -вещественнозначная функция, -большой положительный параметр.Функция -большой положительный параметр.Функция
 может принимать комплексные значения.Будем считать для простоты,что может принимать комплексные значения.Будем считать для простоты,что 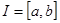 конечный отрезок и что конечный отрезок и что  -достаточно гладкие при -достаточно гладкие при  функции.Тривиальный функции.Тривиальный
случай 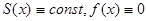 не рассматривается. не рассматривается.

рис.1
Пусть  и достигается только в точке и достигается только в точке  .Тогда функция .Тогда функция  имеет максимум в точке имеет максимум в точке  ,который тем резче,чем больше ,который тем резче,чем больше  (рис.1).Интеграл (рис.1).Интеграл 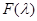 можно приближенно заменить интегралом по малой окрестности точки максимума можно приближенно заменить интегралом по малой окрестности точки максимума  , и это приближение будет тем точнее,чем больше , и это приближение будет тем точнее,чем больше  .В этой окрестности функции .В этой окрестности функции  можно приближенно заменить по формуле Тейлора,и мы получим интеграл,асимптотика которого легко вычисляется.Этот метод был предложен Лапласом. можно приближенно заменить по формуле Тейлора,и мы получим интеграл,асимптотика которого легко вычисляется.Этот метод был предложен Лапласом.
Пусть  .Тогда .Тогда  ;пусть для простоты ;пусть для простоты 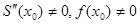 .Тогда .Тогда
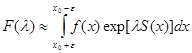 , ,
где 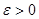 - малое фиксированное число,и - малое фиксированное число,и
 , ,  . .
Следовательно,
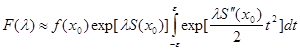 . .
Заметим,что 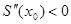 .Последний интеграл равен .Последний интеграл равен
 ( ( ), ),
так как
 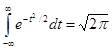 . .
Итак,мы получили асимптотическую формулу
 ( ( ). (1.2) ). (1.2)
Пример 1.Вычислим интеграл
 . ( . ( ). ).
Здесь функция  на отрезке [-1,1] имеет максимум в точке на отрезке [-1,1] имеет максимум в точке  ;также ;также
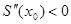 .Все вышеперечисленные условия выполняются, следовательно можно использовать формулу (1.2). .Все вышеперечисленные условия выполняются, следовательно можно использовать формулу (1.2).
 . .
Получили формулу:
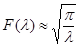 . ( . ( ). ).
Пример 2.Получим асимптотическое разложение гамма-функции Эйлера
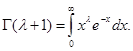
Метод Лапласа непосредственно неприменим к этому интегралу, так как функция  не имеет максимума на данном интервале. не имеет максимума на данном интервале.
Представим подинтегральную функцию в виде

и сделаем замену переменной, положив  .Тогда имеем: .Тогда имеем:
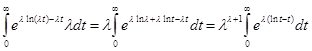 . .
Наш интеграл примет вид:
 . .
Это интеграл Лапласа: здесь  и и 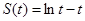 .Функция .Функция  достигает максимума при достигает максимума при  , причем , причем  Поэтому по формуле (1.2) получаем Поэтому по формуле (1.2) получаем
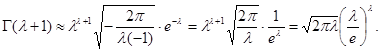
Получили формулу:
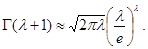
Из этой формулы непосредственно следует формула Стирлинга
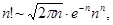
так как 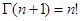 для любого натурального для любого натурального  . .
Пусть теперь  совпадает с одним из концов отрезка, например совпадает с одним из концов отрезка, например  ,и пусть для простоты ,и пусть для простоты  .Заменяя .Заменяя 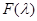 интегралом по отрезку интегралом по отрезку 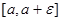 и заменяя приближенно на этом отрезке функции и заменяя приближенно на этом отрезке функции
 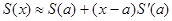 , получаем,что , получаем,что
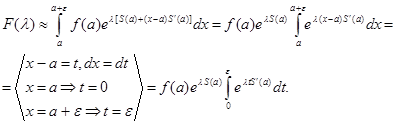
Заметим,что 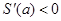 .Вычисляя последний интеграл,получаем .Вычисляя последний интеграл,получаем
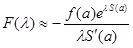 , ( , (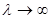 ) (1.3) ) (1.3)
Пример 3.Вычислим интеграл

Здесь функция  на отрезке [0,2] имеет максимум в точке на отрезке [0,2] имеет максимум в точке  ; также ; также
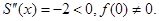 Следовательно, можно применить формулу (1.3): Следовательно, можно применить формулу (1.3):

Получили формулу:
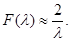
По существу эти две формулы являются основными асимптотическими формулами для интегралов Лапласа.Нам удалось получить простые асимптотические формулы по двум следующим причинам:
1).Подытегральная функция имеет при больших  резкий максимум (т.е. интеграл по отрезку I можно приближенно заменить интегралом по малой окрестности точки максимума). резкий максимум (т.е. интеграл по отрезку I можно приближенно заменить интегралом по малой окрестности точки максимума).
2).В окрестности точки максимума подынтегральную функцию можно заменить более простой (например,такой,что интеграл от нее берется или его асимптотика легко вычисляется).
2.Простейшие оценки Лемма 1.1. Пусть
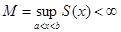
и при некотором 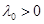 интеграл (1.1) сходится абсолютно: интеграл (1.1) сходится абсолютно:
 . .
Тогда имеет место оценка
 . .
3.Лемма Ватсона
Рассмотрим интеграл Лапласа,в котором S-степенная функция
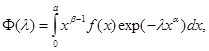 (1.4) (1.4)
где 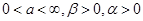 .Так как в окрестности точки максимума S(x) можно приближенно заменить степенной функцией (вообще говоря),то вычисление асимптотики интегралов Лапласа (1.1) сводится к вычислению асимптотики эталонных интегралов (1.4). .Так как в окрестности точки максимума S(x) можно приближенно заменить степенной функцией (вообще говоря),то вычисление асимптотики интегралов Лапласа (1.1) сводится к вычислению асимптотики эталонных интегралов (1.4).
Получим асимптотические оценки для  при при  . Лемма 1.2 (Ватсона).Пусть . Лемма 1.2 (Ватсона).Пусть  .Тогда при .Тогда при  справедливо асимптотическое разложение справедливо асимптотическое разложение
 (1.5) (1.5)
Главный член асимптотики имеет вид
 (1.5´) (1.5´)
Пример 4.Вычислим интеграл
 ( (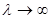 ) )
Здесь 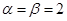 , функция , функция  непрерывна на [0, непрерывна на [0, ] .Применим формулу (1.5´): ] .Применим формулу (1.5´):

Получили формулу:
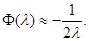 ( (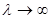 ) )
4.Вклад от граничной точки максимума (основной случай)
Рассмотрим интеграл Лапласа 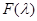 (см.(1.1)). (см.(1.1)).
Теорема 1.1. Пусть  - конечный отрезок и выполнены условия: - конечный отрезок и выполнены условия:
1º.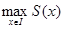 достигается только в точке достигается только в точке 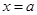 . .
2º. . .
3º.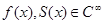 при при 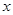 ,близких к ,близких к 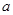 ,и ,и 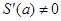 . .
Тогда при  справедливо разложение справедливо разложение
 (1.6) (1.6)
Коэффициенты 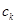 имеет вид имеет вид
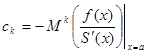 , , 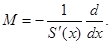 (1.7) (1.7)
Главный член асимптотики имеет вид
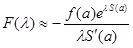 , ( , (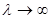 ). ).
Рассмотрим интеграл
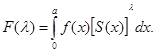 ( (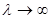 ). ).
Пусть при 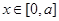 имеем имеем 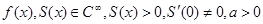 и функция и функция 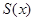 достигает максимума только в точке достигает максимума только в точке  .Тогда при .Тогда при 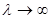 справедлива формула справедлива формула
 . (1.8) . (1.8)
Пример 5.Вычислим интеграл
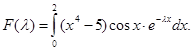
Функция 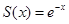 положительна для любого положительна для любого 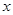 ; ;  и и 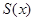 достигает максимума на этом отрезке в точке 0.Применяя формулу (1.8), получим достигает максимума на этом отрезке в точке 0.Применяя формулу (1.8), получим
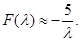
Пусть [a,b]- конечный отрезок  и пусть функция и пусть функция 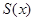 достигает достигает
максимума только в точке  .Тогда для интеграла .Тогда для интеграла
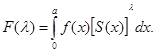 ( (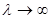 ). ).
справедлива формула

где  , если , если  ; ;  , если , если  совпадает с одним из концов отрезка. совпадает с одним из концов отрезка.
Пример 6. Найдем асимптотику при 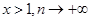 полинома Лежандра полинома Лежандра

где 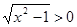 . .
В данном случае  . Функция . Функция 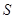 достигает максимума при достигает максимума при
 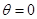 и и  По последней формуле По последней формуле
находим, что
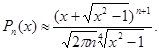
Пример 7.Покажем, что при 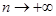

Здесь 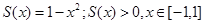 , , .Применяя последнюю формулу, .Применяя последнюю формулу,
получим
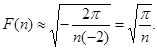
5.Вклад от внутренней невырожденной точки максимума
Теорема 1.2. Пусть  - конечный отрезок и выполнены условия: - конечный отрезок и выполнены условия:
1º.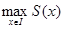 достигается только в точке достигается только в точке  . .
2º. . .
3º.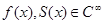 при при 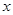 ,близких к ,близких к 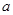 ,и ,и 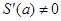 . .
Тогда при  справедливо разложение справедливо разложение
 (1.9) (1.9)
Коэффициенты 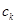 имеет вид имеет вид
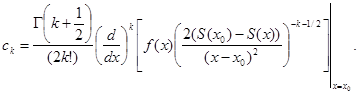 (1.10) (1.10)
Главный член асимптотики (1.9) имеет вид
 ( ( ). ).
Теорема 1.3. Пусть все условия теоремы 1.2 выполнены, за исключением одного: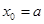 . .
Тогда при  справедливо разложение справедливо разложение
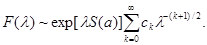 (1.11) (1.11)
Главный член асимптотики имеет вид
 . (1.12) . (1.12)
Пример 8.Покажем, что при 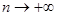
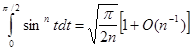 . .
Имеем  , так что интеграл имеет вид интеграла Лапласа (1.1), , так что интеграл имеет вид интеграла Лапласа (1.1),
где 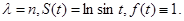 Функция Функция  достигает максимума при достигает максимума при 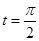 , причем , причем

Интеграл выяисляется по формуле (1.12):
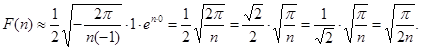
Получили формулу:

Пример 9. Покажем, что при 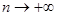
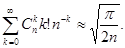
Воспользуемся тождеством
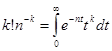 . .
Тогда сумма примет вид
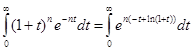 . .
В данном случае  ; остается применить теорему 1.3. ; остается применить теорему 1.3.
6.Программа и численные результаты
Следующая программа вычисляет интеграл по формуле Симпсона и методом Лапласа:
unit Main;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls, ComCtrls;
type
TForm1 = class(TForm)
GroupBox1: TGroupBox;
Label1: TLabel;
Edit1: TEdit;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Edit2: TEdit;
Edit3: TEdit;
Edit4: TEdit;
Label5: TLabel;
StatusBar1: TStatusBar;
Button1: TButton;
Button2: TButton;
GroupBox2: TGroupBox;
Panel1: TPanel;
Panel2: TPanel;
Label6: TLabel;
Label7: TLabel;
procedure Edit1MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
procedure Edit2MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
procedure Edit3MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
procedure Edit4MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
procedure FormMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button1MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
procedure Button2MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
x,v,a,b,r,r2,h,eps,lam,lap: extended;
n: integer;
implementation
{$R *.dfm}
procedure TForm1.Edit1MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
StatusBar1.SimpleText:='Введитенижнююграницу';
end;
procedure TForm1.Edit2MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
StatusBar1.SimpleText:='Введитеверхнююграницу';
end;
procedure TForm1.Edit3MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
StatusBar1.SimpleText:='ВведитеточностьдляметодаСимпсона';
end;
procedure TForm1.Edit4MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
StatusBar1.SimpleText:='ВведитепараметрвинтегралеЛапласа';
end;
procedure TForm1.FormMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
StatusBar1.SimpleText:='';
end;
function f(x,lam:extended):extended; //Подинтегральнаяфункция
begin
f:=(sin(x)+4)*exp(-2*lam*x);
end;
function simpson(a,b:extended;n:integer):extended;
var s,h:extended;
m,mn:integer;
begin
h:=(b-a)/n;
s:=f(a,lam)+f(b,lam);
mn:=4;
for m:=1 to n-1 do begin
s:=s+mn*f(a+h*m,lam);
if (mn=4) then mn:=2 else mn:=4;
end;
simpson:=s*h/3;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
a:=StrToFloat(Edit1.Text);
b:=StrToFloat(Edit2.Text);
eps:=StrToFloat(Edit3.Text);
lam:=StrToFloat(Edit4.Text);
n:=3;
r:=simpson(a,b,n);
repeat r2:=r;
n:=n+2;
r:=simpson(a,b,n); h:=(b-a)/n;
until (abs(r-r2)<eps);
Panel1.Caption:=FloatToStr(r);
lap:=2/lam;
Panel2.Caption:=FloatToStr(lap);
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
Close;
end;
procedure TForm1.Button1MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
StatusBar1.SimpleText:='Вычислениеинтеграла';
end;
procedure TForm1.Button2MouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
StatusBar1.SimpleText:='Выходизпрограммы';
end;
end.

Пример 3.Для интеграла

при  получены результаты: получены результаты:

Пример 1.Для интеграла

получены результаты:

Пример 4.Для интеграла

получены результаты:

Список литературы
Федорюк М.В. «Асимптотика: интегралы и ряды». М.:Наука, 1977.
|