Введение
Гидростатика – это раздел гидравлики (механики жидкости), изучающий покоящиеся жидкости. Она изучает законы равновесия жидкости и распределения в ней давления. Основные величины, используемые в гидростатике, – это давление p
и напор H
.
В гидравлике при изучении законов равновесия и движения широко пользуются различными физическими характеристиками жидкости (например, плотность, вязкость, удельный вес, удельный объём). Студенту нужно уметь определять основные физические характеристики жидкости, знать единицы этих характеристик. Следует также рассмотреть основные физические свойства капельных жидкостей: сжимаемость, тепловое расширение и др.
1. Физические свойства жидкости
Существуют следующие физические свойства жидкости:
1) Плотность 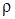 – это масса единицы объёма жидкости (кг/м3
): – это масса единицы объёма жидкости (кг/м3
):
r =
m
/
V
,
где m
– масса, кг;
V –
объём, м3
.
Плотность воды при температуре +4°С равна 1000кг/м3
. Легко заметить, что плотность воды зависит от температуры незначительно. В большинстве гидравлических расчётов свойствами сжимаемости и температурного расширения жидкостей пренебрегают, например, для воды считают плотность постоянной и равной 1000 кг/м3
.
2) Удельный вес – это вес единицы объёма жидкости (Н/м3
):
g =
G
/
V
,
где G
– вес (сила тяжести), Н
;
V –
объём, м3
.
Связаны удельный вес и плотность через ускорение свободного падения (g =
9,81 » 10 м/с2
) так:
g=
rg
.
3) Коэффициент объёмного сжатия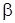 w
(Па-1
) –
это относительное изменение объёма жидкости при изменении давления на единицу: w
(Па-1
) –
это относительное изменение объёма жидкости при изменении давления на единицу:
 , ,
где D
W
– изменение объёма W
;
Dr– изменение плотности r, соответствующее изменению давления на величину Dp
.
Величина, обратная коэффициенту объёмного сжатия, называется модулем упругости жидкостей E
ж
(Па):
Е
ж
=
1/ 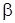 W
. W
.
Значение модуля упругости жидкостей зависит от давления и температуры. Если принять, что приращение давления D
p
=
p
–
p
0
, а изменение объёма D
W
=
W
-
W
0
, то:
W
=W
0
·(1-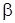 W
·Dp
), W
·Dp
),
r =r0
·(1-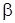 W
·Dp
). W
·Dp
).
4) Коэффициент температурного расширения 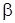 t
(0
С)-1
выражает относительное изменение объёма жидкости при изменении температуры на один градус: t
(0
С)-1
выражает относительное изменение объёма жидкости при изменении температуры на один градус:
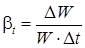 , ,
где DW
– изменение объёма W
, соответствующее изменению температуры на величину D t
.
Коэффициент температурного расширения воды увеличивается с возрастанием температуры и давления; для большинства других капельных жидкостей bt
с увеличением давления уменьшается. Если принять, что приращение температуры D
t = t – t0
, а изменение объёма D
W = W – W
0
, то:
W
=
W
0
(1+
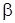 t
-Dt
), t
-Dt
),
r =
r0
(1+
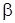 t
·Dt
). t
·Dt
).
5) Вязкость –
это свойство жидкости проявлять внутреннее трение при её движении, обусловленное сопротивлением взаимному сдвигу её частиц. В покоящейся жидкости вязкость не проявляется. Количественно вязкость может быть выражена в виде динамической или кинематической вязкости, которые легко переводятся одна в другую.
Вязкость динамическая m, Па·
с =
Н·
с/м2
. Динамический коэффициент вязкости µ не зависит от давления и от характера движения, а определяется лишь физическими свойствами жидкости и её температурой.
В практике для характеристики вязкости жидкости чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости 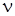 (м2
/с). Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости: (м2
/с). Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости:
Вязкость кинематическая 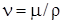 , м2
/с. , м2
/с.
Вязкость проявляется в том, что при движении жидкости возникает сила внутреннего трения Т
между перемещающимися один относительно другого слоями с площадью соприкосновения S
.
определяется законом Ньютона:
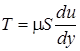 , ,
где S –
площадь соприкасающихся слоёв, м2
;
du –
скорость смещения слоя «b
» относительно слоя «a
», м/с;
dy –
расстояние, на котором скорость движения слоёв изменилась на du
, м;
du
/
dy
–
градиент скорости, изменение скорости по нормали к направлению движения (с
-1
).
Если силу трения T
отнести к единице площади соприкасающихся слоёв, то получим величину касательного напряжения 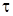 , которую можно определить по формуле: , которую можно определить по формуле:
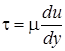 . .
Вязкость жидкости определяют при помощи вискозиметра Энглера и выражают в градусах Энглера (0
Е). Градус Энглера (0
Е) есть отношение времени истечения испытуемой жидкости ко времени истечения дистиллированной воды. Для перехода от вязкости в градусах Энглера к коэффициенту кинематической вязкости
применяется формула Убеллоде:
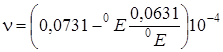 . .
Вязкость также определяют капиллярным вискозиметром Оствальда. Коэффициент кинематической вязкости определяют по формуле:
n =
c
·
T
ж
·
10-4
,
где с
– постоянная прибора;
T
ж
– время истечения жидкости, с.
2. Гидростатическое давление
Гидростатическое давление p –
это скалярная величина, характеризующая напряжённое состояние жидкости. Давление равно модулю нормального напряжения в точке: p =
/s /.
Давление в системе СИ измеряется в паскалях: Па = Н/м2
.
Связь единиц давления в различных системах измерения такая:
100 000 Па = 0,1 МПа = 1 кгс/см2
= 1 ат = 10 м вод. ст.
Два свойства гидростатического давления:
1. Давление в покоящейся жидкости на контакте с твёрдым телом вызывает напряжения, направленные перпендикулярно к поверхности раздела.
2. Давление в любой точке жидкости действует одинаково по всем направлениям. Это свойство отражает скалярность давления.
2.1 Гидростатический парадокс
Суммарное давление на горизонтальное дно зависит только от глубины погружения дна h
0
и величины площади последнего и не зависит от формы сосуда, а следовательно, и от веса налитой в эти сосуды жидкости. На рис. 1 показано несколько сосудов личных форм с плоским дном площадью 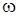 глубиной жидкости в них h
,одинаковыми для всех сосудов. глубиной жидкости в них h
,одинаковыми для всех сосудов.

Рис. 1. Гидростатический парадокс
Различные формы стенок сосудов и различные веса жидкости в этих сосудах не оказывают никакого влияния на величину суммарного давления на их дно, равного для всех сосудов согласно:
p
= 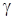 h h .
.
Это кажущееся противоречие известно под названием гидростатического парадокса. Объясняется это явление тем, что разность между силой давления на горизонтальное дно.
2.2 Основное уравнение гидростатики
Основное уравнение гидростатики гласит, что полное давление в жидкости p
равно сумме внешнего давления на жидкость p
0
и давления веса столба жидкости p
ж
, то есть
p
=
p
0
+
p
ж
=
p
0
+
gh
,
где h
– высота столба жидкости над точкой (глубина её погружения), в которой определяется давление (рис. 2).
Из уравнения следует, что давление в жидкости увеличивается с глубиной и зависимость является линейной.

Рис. 2. Схема к основному уравнению гидростатики
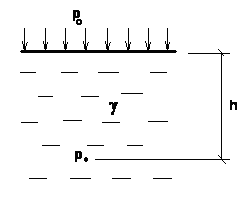
Рис. 3. Изменение давления: 1 – открытый резервуар; 2 – пьезометр
В частном случае для открытых резервуаров, сообщающихся с атмосферой (рис. 3), внешнее давление на жидкость равно атмосферному давлению p
o
= p
атм
= 101 325 Па 1 ат. Тогда основное уравнение гидростатики принимает вид: 1 ат. Тогда основное уравнение гидростатики принимает вид:
p
=
p
атм
+
gh
.
Открытые резервуары –
это не только баки, ёмкости, сообщающиеся с атмосферой, но также любые канавы с водой, озёра, водоёмы и т.д.
Избыточное давление (манометрическое) есть разность между полным и атмосферным давлением. Из последнего уравнения получаем, что для открытых резервуаров избыточное давление равно давлению столба жидкости:
p
изб
=
p
ман
=
p
-
p
атм
=
gh
.
3. Вакуум
Рассмотрим два сосуда I и II (риc. 4), соединённые между собой. Сосуд II заполнен жидкостью и имеет давление на свободной поверхности, равное атмосферному P
A
. Из сосуда I, постепенно откачивая воздух, создадим разрежение с давлением Р
РАЗР
меньше атмосферного. Тогда жидкость из сосуда II начнёт подниматься (всасываться) по трубке.

Рис. 4. Определение величины вакуума
Пусть при каком-то Р
разр
уровень в трубке поднялся на величину hV
.
Рассмотрим равновесие частиц жидкости в трубке на уровне а – а
. Так как частицы жидкости в трубке на уровне а – а
находятся в равновесии, то это значит, что давление со стороны сосуда I
, равное Р
разр
+ г hV
, и давление состороны сосуда II
, равное PA
,между собой равны.
В этом случае можно написать, что Р
разр
+ г hV
= PA
.
отсюда:
PA
– Р
разр
= г hV
= PV
.
Разность между атмосферным PA
и абсолютным давлением Р
разр
, когда оно меньше атмосферного, называется вакуумметрическим давлением,
или вакуумом.
Иначе, вакуум – это недостаток давления до атмосферного.
Вакуум измеряется в тех же единицах, что и гидростатическое давление. Вакуум можно измерить и высотой столба жидкости. Вакуум встречается в насосах и иных гидравлических аппаратах и сооружениях, например в сифонах, и т.п.
Теоретически наибольшая величина вакуума может быть равна 1 кгc/см2
, или 10,33 м вод. ст., или 101,3 кН/м2
. Практически такой величины вакуума добиться нельзя, так как абсолютное разрежение над жидкостью создать невозможно, потому что в пространстве над жидкостью неизбежно будут пары жидкости и выделяющийся из жидкости растворённый воздух. Поэтому при перекачке холодной воды величина вакуума практически в насосах бывает не более 7 м вод. ст., при перекачке горячей воды и лёгких жидкостей – значительно меньше.
4. Приборы для измерения давления
Давление в жидкости измеряется приборами:
– пьезометрами;
– манометрами;
– вакуумметрами.
Пьезометры и манометры измеряют избыточное (манометрическое) давление, то есть они работают, если полное давление в жидкости превышает величину, равную одной атмосфере p =
1кгс/см2
=
0,1МПа. Эти приборы показывают долю давления сверх атмосферного. Для измерения в жидкости полного давления p
необходимо к манометрическому давлению p
ман
прибавить атмосферное давление p
атм
, снятое с барометра. Практически же в гидравлике атмосферное давление считается величиной постоянной p
атм
=
101325»
100000Па.
Пьезометр обычно представляет собой вертикальную стеклянную трубку, нижняя часть которой сообщается с исследуемой точкой в жидкости, где нужно измерить давление (например, точка А на рис. 3), а верхняя её часть открыта в атмосферу. Высота столба жидкости в пьезометре hp
является показанием этого прибора и позволяет измерять избыточное (манометрическое) давление в точке по соотношению:
жидкость гидростатический вакуум давление
p
изб
=
ghp
.
где hp
– пьезометрический напор (высота), м.
Упомянутые пьезометры применяются главным образом для лабораторных исследований. Их верхний предел измерения ограничен высотой до 5 м, однако их преимущество перед манометрами состоит в непосредственном измерении давления с помощью пьезометрической высоты столба жидкости без промежуточных передаточных механизмов.
В качестве пьезометра может быть использован любой колодец, котлован, скважина с водой или даже любое измерение глубины воды в открытом резервуаре, так как оно даёт нам величину hp
.
Манометрычаще всего применяются механические, реже – жидкостные. Все манометры измеряют не полное давление, а избыточное:
p
ман
=
p
изб
=
p
-
p
атм
.
Преимуществами их перед пьезометрами являются более широкие пределы измерения, однако есть и недостаток: они требуют контроля их показаний. Манометры, выпускаемые в последнее время, градуируются в единицах СИ: МПа или кПа. Однако ещё продолжают применяться и старые манометры со шкалой в кгс/см2
, они удобны тем, что эта единица равна одной атмосфере. Нулевое показание любого манометра соответствует полному давлению p
, равному одной атмосфере.
Вакуумметр по своему внешнему виду напоминает манометр, а показывает он ту долю давления, которая дополняет полное давление в жидкости до величины одной атмосферы. Вакуум в жидкости – это не пустота, а такое состояние жидкости, когда полное давление в ней меньше атмосферного на величину p
в
, которая измеряется вакуумметром. Вакуумметрическое давление p
в
, показываемое прибором, связано с полным и атмосферным так:
p
в
=
p
атм
–
p
.
Величина вакуума p
в
не может быть больше 1 атм, то есть предельное значение p
в
 100000Па, так как полное давление не может быть меньше абсолютного нуля.
100000Па, так как полное давление не может быть меньше абсолютного нуля.
Приведём примеры снятия показаний с приборов:
– пьезометр, показывающий hp
=
160см вод. ст., соответствует в единицах СИ давлениям p
изб
=
16000Па и p=
100000+ 16000= =116000 Па;
– манометр с показаниями p
ман
=
2,5кгс/см2
соответствует водяному столбу hp
=
25 м и полному давлению в СИ p =
0,35МПа;
– вакуумметр, показывающий p
в
=
0,04МПа, соответствует полному давлению p=
100 000–40 000=60 000Па, что составляет 60% от атмосферного.
5. Эпюры давления жидкости
Эпюра давления жидкости – это графическое изображение распределения давления жидкости по твёрдой поверхности, соприкасающейся с ней. Примеры эпюр для плоских и криволинейных поверхностей приведены на рис. 5 и 6. Стрелками на эпюре показывают направление действия давления (вернее, направление нормальных напряжений, возникающих от действия давления, так как по 2-му свойству давление скалярно). Величина стрелки (ордината) откладывается в масштабе и количественно показывает величину давления.

Рис. 5. Эпюры давления жидкости на плоские поверхности

Рис. 6. Эпюры давления жидкости на криволинейную поверхность
Эпюры давления жидкости на плоские поверхности служат исходными данными для проведения расчётов на прочность и устойчивость конструкций, взаимодействующих с жидкостями: стенок плавательных бассейнов, баков, резервуаров, цистерн. Расчёты ведутся методами сопротивления материалов и строительной механики.
В большинстве случаев строят эпюры избыточного давления вместо полного, а атмосферное не учитывают из-за его взаимного погашения с той и другой стороны ограждающей конструкции. При построении таких эпюр для плоских и криволинейных поверхностей (см. рис. 5 и 6) используют линейную зависимость давления от глубины p
изб
= gh
и 1-е свойство гидростатического давления.
Библиографический список
1. Тимченко, В.И. Гидравлика: практикум для студентов / В.И. Тимченко; Южно-Рос. гос. ун-т экономики и сервиса. – Шахты: ЮРГУЭС, 2010. – 41 с.
2. Гидравлика. Гидравлические и пневматические системы: практикум / В.И. Тимченко. – Шахты: Изд-во ЮРГУЭС, 2008. – 53 с.
3. Гидравлика. Гидравлические и пневматические системы в автомобилях и гаражном оборудовании: практикум / В.И. Тимченко, И.К. Гугуев, А.И. Шилин, А.Г. Илиев. – Шахты: Изд-во ЮРГУЭС, 2008. – 53 с.
4. Гидравлика, гидромашины и гидропневмопривод: учеб. пособие для вузов / Т.В. Артемьева [и др.]; под ред. С.П. Стесина. – М.: Академия, 2009. – 336 с.
5. Сологаев, В.И. Механика жидкости и газа: конспекты лекций / В.И. Сологаев; СибАДИ. – Омск, 2010. – 56 с.
6. Механика жидкости и газа: пособие / К.Г. Донец; Южно-Рос. гос. ин-т экономики и сервиса (филиал). – Шахты: ЮРГУЭС, 2008. – 48 с.
7. Башта, Т.М. Гидравлика, гидромашины и гидроприводы: учебник для вузов / Т.М. Башта, С.С. Руднев, Б.Б. Некрасов [и др.]. – 2-е изд., перераб. – М.: Машиностроение, 2010. – 423 с.
8. Сапронов, А.Г. Энергосбережение на предприятиях бытового обслуживания: учеб. пособие / А.Г. Сапронов, В.А. Шаповалов; под ред. А.Г. Сапронова. – Шахты: Изд-во ЮРГУЭС, 2009. – 115 с.
9. Гидравлика, гидромашины и гидропневмопривод: учеб. пособие для вузов / Т.В. Артемьева [и др.]; под ред. С.П. Стесина. – 3-е изд., стер. – М.: Академия, 2008. – 336 с.
|