Цепи Маркова
Содержание
Введение
§ 1. Цепь Маркова
§ 2. Однородная цепь Маркова. Переходные вероятности. Матрица перехода
§3. Равенство Маркова
§4. Стационарное распределение. Теорема о предельных вероятностях
§5. Доказательство теоремы о предельных вероятностях в цепи Маркова
§6. Области применения цепей Маркова
Заключение
Список использованной литературы
Введение
Тема нашей курсовой работы цепи Маркова. Цепи Маркова названы так в честь выдающегося русского математика, Андрея Андреевича Маркова, который много занимался случайными процессами и внес большой вклад в развитие этой области. В последнее время можно услышать о применении цепей Маркова в самых разных областях: современных веб-технологиях, при анализе литературных текстов или даже при разработке тактики игры футбольной команды. У тех, кто не знает что такое цепи Маркова, может возникнуть ощущение, что это что-то очень сложное и почти недоступное для понимания.
Нет, все как раз наоборот. Цепь Маркова это один из самых простых случаев последовательности случайных событий. Но, несмотря на свою простоту, она часто может быть полезной даже при описании довольно сложных явлений. Цепью Маркова называют такую последовательность случайных событий, в которой вероятность каждого события зависит только от предыдущего, но не зависит от более ранних событий.
Прежде чем углубиться, нужно рассмотреть несколько вспомогательных вопросов, которые общеизвестны, но совершенно необходимы для дальнейшего изложения.
Задача моей курсовой работы – более подробно изучить приложения цепей Маркова, постановку задачи и проблемы Маркова.
§1. Цепь Маркова
Представим, что производится последовательность испытаний.
Определение.
Цепью Маркова называют последовательность испытаний, в каждом из которых появляется одно и только одно из 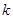 несовместных событий несовместных событий  полной группы, причем условная вероятность полной группы, причем условная вероятность 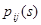 того, что в того, что в  -м испытании наступит событие -м испытании наступит событие  , при условии, что в , при условии, что в  -м испытании наступило событие -м испытании наступило событие  , не зависит от результатов предшествующих испытаний. , не зависит от результатов предшествующих испытаний.
Например, если последовательность испытаний образует цепь Маркова и полная группа состоит из четырех несовместных событий  , причем известно, что в шестом испытании появилось событие , причем известно, что в шестом испытании появилось событие 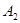 , то условная вероятность того, что в седьмом испытании наступит событие , то условная вероятность того, что в седьмом испытании наступит событие  , не зависит от того, какие события появились в первом, втором, …, пятом испытаниях. , не зависит от того, какие события появились в первом, втором, …, пятом испытаниях.
Заметим, что независимые испытания являются частным случаем цепи Маркова. Действительно, если испытания независимы, то появление некоторого определенного события в любом испытании не зависит от результатов ранее произведенных испытаний. Отсюда следует, что понятие цепи Маркова является обобщением понятия независимых испытаний.
Часто при изложении теории цепей Маркова придерживаются иной терминология и говорят о некоторой физической системе 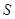 , которая в каждый момент времени находится в одном из состояний: , которая в каждый момент времени находится в одном из состояний:  , и меняет свое состояние только в отдельные моменты времени , и меняет свое состояние только в отдельные моменты времени  то есть система переходит из одного состояния в другое ( например из то есть система переходит из одного состояния в другое ( например из 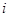 в в  ). Для цепей Маркова вероятность перейти в какое-либо состояние ). Для цепей Маркова вероятность перейти в какое-либо состояние  в момент в момент  зависит только от того, в каком состоянии система находилась в момент зависит только от того, в каком состоянии система находилась в момент  , и не изменяется от того, что становятся известными ее состояния в более ранние моменты. Так же в частности, после испытания система может остаться в том же состоянии («перейти» из состояния , и не изменяется от того, что становятся известными ее состояния в более ранние моменты. Так же в частности, после испытания система может остаться в том же состоянии («перейти» из состояния 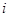 в состояние в состояние 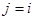 ). ).
Для иллюстрации рассмотрим пример.
Пример 1.
Представим, что частица, находящаяся на прямой, движется по этой прямой под влиянием случайных толчков, происходящих в моменты 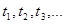 . Частица может находиться в точках с целочисленными координатами: . Частица может находиться в точках с целочисленными координатами:  ; в точках ; в точках  и и  находятся отражающие стенки. Каждый толчок перемещает частицу вправо с вероятностью находятся отражающие стенки. Каждый толчок перемещает частицу вправо с вероятностью  и влево с вероятностью и влево с вероятностью  , если только частица не находится у стенки. Если же частица находится у стенки, то любой толчок переводит ее на единицу внутрь промежутка между стенками. Здесь мы видим, что этот пример блуждания частицы представляет собой типичную цепь Маркова. , если только частица не находится у стенки. Если же частица находится у стенки, то любой толчок переводит ее на единицу внутрь промежутка между стенками. Здесь мы видим, что этот пример блуждания частицы представляет собой типичную цепь Маркова.
Таким образом, события называют состояниями системы, а испытания – изменениями ее состояний.
Дадим теперь определение цепи Маркова, используя новую терминологию.
Цепью Маркова с дискретным временем называют цепь, изменение состояний которой происходит в определенные фиксированные моменты времени.
Цепью Маркова с непрерывным временем называют цепь, изменение состояний которой происходит в любые случайные возможные моменты времени.
§2. Однородная цепь Маркова. Переходные вероятности. Матрица перехода
Определение.
Однородной называют цепь Маркова, если условная вероятность 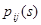 (переход из состояния (переход из состояния 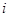 в состоянии в состоянии  ) не зависит от номера испытания. Поэтому вместо ) не зависит от номера испытания. Поэтому вместо 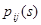 пишут просто пишут просто 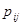 . .
Пример 1.
Случайное блуждание. Пусть на прямой 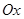 в точке с целочисленной координатой находится материальная частица. В определенные моменты времени частица испытывает толчки. Под действием толчка частица с вероятностью в точке с целочисленной координатой находится материальная частица. В определенные моменты времени частица испытывает толчки. Под действием толчка частица с вероятностью  смещается на единицу вправо и с вероятностью смещается на единицу вправо и с вероятностью  – на единицу влево. Ясно, что положение (координата) частицы после толчка зависит от того, где находилась частица после непосредственно предшествующего толчка, и не зависит от того, как она двигалась под действием остальных предшествующих толчков. – на единицу влево. Ясно, что положение (координата) частицы после толчка зависит от того, где находилась частица после непосредственно предшествующего толчка, и не зависит от того, как она двигалась под действием остальных предшествующих толчков.
Таким образом, случайное блуждание − пример однородной цепи Маркова с дискретным временем.
Далее ограничимся элементами теории конечных однородных цепей Маркова.
Переходной вероятностью 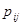 называют условную вероятность того, что из состояния называют условную вероятность того, что из состояния 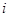 (в котором система оказалась в результате некоторого испытания, безразлично какого номера) в итоге следующего испытания система перейдет в состояние (в котором система оказалась в результате некоторого испытания, безразлично какого номера) в итоге следующего испытания система перейдет в состояние  . .
Таким образом, в обозначении 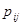 первый индекс указывает номер предшествующего, а второй − номер последующего состояния. Например, первый индекс указывает номер предшествующего, а второй − номер последующего состояния. Например,  – вероятность перехода из второго состояния в третье. – вероятность перехода из второго состояния в третье.
Пусть число состояний конечно и равно 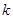 . .
Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

Так как в каждой строке матрицы помещены вероятности событий (перехода из одного и того же состояния 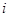 в любое возможное состояние в любое возможное состояние  ), которые образуют полную группу, то сумма вероятностей этих событий равна единице. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице: ), которые образуют полную группу, то сумма вероятностей этих событий равна единице. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице:
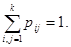
Приведем пример матрицы перехода системы, которая может находиться в трех состояниях 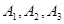 ; переход из состояния в состояние происходит по схеме однородной цепи Маркова; вероятности перехода задаются матрицей: ; переход из состояния в состояние происходит по схеме однородной цепи Маркова; вероятности перехода задаются матрицей:

Здесь видим, что если система находилось в состоянии 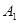 , то после изменения состояния за один шаг она с вероятностью 0,5 останется в этом же состоянии, с вероятностью 0,5 останется в этом же состоянии, с вероятностью 0,2 перейдет в состояние , то после изменения состояния за один шаг она с вероятностью 0,5 останется в этом же состоянии, с вероятностью 0,5 останется в этом же состоянии, с вероятностью 0,2 перейдет в состояние 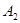 , то после перехода она может оказаться в состояниях , то после перехода она может оказаться в состояниях  ; перейти же из состояния ; перейти же из состояния 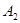 в в 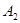 она не может. Последняя строка матрицы показывает нам, что из состояния она не может. Последняя строка матрицы показывает нам, что из состояния  перейти в любое из возможных состояний с одной и той же вероятностью 0,1. перейти в любое из возможных состояний с одной и той же вероятностью 0,1.
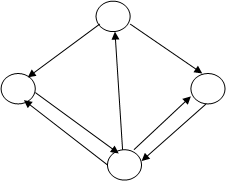
На основе матрицы перехода системы можно построить так называемый граф состояний системы,его еще называют размеченный граф состояний. Это удобно для наглядного представления цепи. Порядок построения граф рассмотрим на примере.
Пример 2.
По заданной матрице перехода построить граф состояний.

Т.к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния.
S1
0,2 0,7
S2 0,4 S4
0,6 0,5
0,1 0,5
S3
На графе не отмечаются вероятности перехода системы из одного состояния в то же самое. При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы.
§3. Равенство Маркова
Определение.
Обозначим через  вероятность того, что в результате вероятность того, что в результате  шагов (испытаний) система перейдет из состояния шагов (испытаний) система перейдет из состояния 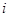 в состояние в состояние  . Например, . Например,  – вероятность перехода за 10 шагов из второго состояния в пятое. – вероятность перехода за 10 шагов из второго состояния в пятое.
Подчеркнем, что при  получим переходные вероятности получим переходные вероятности
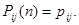
Поставим перед собой задачу: зная переходные вероятности 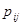 найти вероятности найти вероятности  перехода системы из состояния перехода системы из состояния 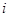 в состояние в состояние  за за  шагов. шагов.
С этой целью введем в рассмотрение промежуточное (между 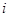 и и  ) состояние ) состояние  . Другими словами, будeм считать, что из первоначального состояния . Другими словами, будeм считать, что из первоначального состояния 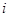 за за  шагов система перейдет в промежуточное состояние шагов система перейдет в промежуточное состояние  с вероятностью с вероятностью 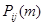 , после чего за оставшиеся , после чего за оставшиеся 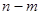 шагов из промежуточного состояния шагов из промежуточного состояния  она перейдет в конечное состояние она перейдет в конечное состояние  с вероятностью с вероятностью 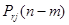 . .
По формуле полной вероятности, получим
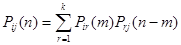 . (1) . (1)
Эту формулу называют равенством Маркова.
Пояснение.
Введем обозначения:
 – интересующее нас событие (за – интересующее нас событие (за  шагов система перейдет из начального состояния шагов система перейдет из начального состояния 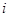 в конечное в конечное  ), следовательно, ), следовательно,  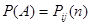 ; ; 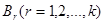 − гипотезы( за − гипотезы( за  шагов система перейдет из первоначального состояния шагов система перейдет из первоначального состояния 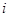 в промежуточное состояние в промежуточное состояние  ), следовательно, ), следовательно,  − условная вероятность наступления − условная вероятность наступления  при условии, что имела место гипотеза при условии, что имела место гипотеза 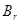 (за (за 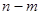 шагов система перейдет из промежуточного состояния шагов система перейдет из промежуточного состояния  в конечное в конечное  ), следовательно, ), следовательно, 
По формуле полной вероятности,
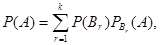 ( (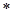 ) )
Или в принятых нами обозначениях
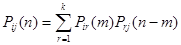
что совпадает с формулой Маркова (1).
Зная все переходные вероятности  т.е зная матрицу т.е зная матрицу  перехода из состояния в состояние за один шаг, можно найти вероятности перехода из состояния в состояние за один шаг, можно найти вероятности  перехода из состояния в состояние за два шага, следовательно, и саму матрицу перехода перехода из состояния в состояние за два шага, следовательно, и саму матрицу перехода  ; по известной матрице ; по известной матрице  можно найти матрицу можно найти матрицу  перехода из состояния в состояние за три шага, и т.д. перехода из состояния в состояние за три шага, и т.д.
Действительно, положив  в равенстве Маркова в равенстве Маркова
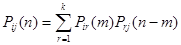 , ,
Получим
цепь марков случайный вероятность
 , ,
Или
 (2) (2)
Таким образом, по формуле (2) можно найти все вероятности  следовательно, и саму матрицу следовательно, и саму матрицу  . Поскольку непосредственное использование формулы (2) оказывается утомительным, а матричное исчисление ведет к цели быстрее, напишу вытекающие из (2) соотношение в матричной форме: . Поскольку непосредственное использование формулы (2) оказывается утомительным, а матричное исчисление ведет к цели быстрее, напишу вытекающие из (2) соотношение в матричной форме:

Положив 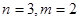 в (1), аналогично получим в (1), аналогично получим

В общем случае

Теорема 1.
При любых s, t
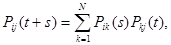  (3) (3)
Доказательство. Вычислим вероятность  по формуле полной вероятности ( по формуле полной вероятности (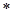 ), положив ), положив 
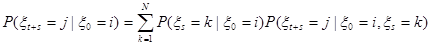 (4) (4)
Из равенств
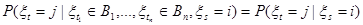
и 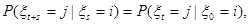 
следует
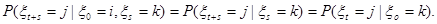
Отсюда из равенств (4) и
 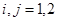
получим утверждение теоремы.
Определим матрицу  В матричной записи (3) имеет вид В матричной записи (3) имеет вид
 (5) (5)
Так как 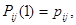 то то  где где  − матрица вероятности перехода. Из (5) следует − матрица вероятности перехода. Из (5) следует
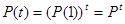 (6) (6)
Результаты, полученной в теории матриц, позволяют по формуле (6) вычислить  и исследовать их поведение при и исследовать их поведение при  
Пример 1.
Задана матрица перехода 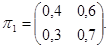 Найти матрицу перехода Найти матрицу перехода 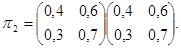
Решение. Воспользуемся формулой 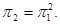
Перемножив матрицы, окончательно получим:
 . .
§4. Стационарное распределение. Теорема о предельных вероятностях
Распределение вероятностей  в произвольной момент времени в произвольной момент времени  можно найти, воспользовавшись формулой полной вероятности можно найти, воспользовавшись формулой полной вероятности
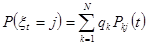 (7) (7)
Может оказаться, что 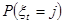 не зависит от времени. Назовем стационарным распределением
вектор не зависит от времени. Назовем стационарным распределением
вектор 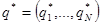 , удовлетворяющий условиям , удовлетворяющий условиям
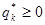 , , 
 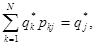 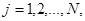 (8) (8)
где  вероятности перехода. вероятности перехода.
Если в цепи Маркова  то при любом то при любом 
 
Это утверждение следует по индукции из (7) и (8).
Приведем формулировку теоремы о предельных вероятностях для одного важного класса цепей Маркова.
Теорема 1.
Если при некотором 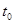 >0 все элементы матрица >0 все элементы матрица  положительны, то для любых положительны, то для любых 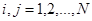 , при , при 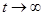
 , (9) , (9)
где 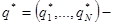 стационарное распределение с стационарное распределение с   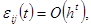 а а  некоторая постоянная, удовлетворяющая неравенством 0<
h
<1. некоторая постоянная, удовлетворяющая неравенством 0<
h
<1.
Так как  , то по условию теоремы из любого состояния можно попасть в любое за время , то по условию теоремы из любого состояния можно попасть в любое за время 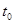 с положительной вероятностью. Условия теоремы исключает цепи, являющиеся в некотором смысле периодическими. с положительной вероятностью. Условия теоремы исключает цепи, являющиеся в некотором смысле периодическими.
Если выполнить условие теоремы 1, то вероятность того, что система находится в некотором состоянии  , в пределе не зависит от начального распределение. Действительно, из (9) и (7) следует, что при любом начальном распределении , в пределе не зависит от начального распределение. Действительно, из (9) и (7) следует, что при любом начальном распределении 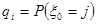 , , 
  
Рассмотрим несколько примеров цепи Маркова, которых условия теоремы 1, не выполнены. Нетрудно проверить, что такими примерами является примеры . В примере 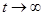 вероятности перехода имеют приделы, но эти приделы зависят от начального состояния. В частности, при вероятности перехода имеют приделы, но эти приделы зависят от начального состояния. В частности, при 
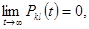 0< 0< < < , ,  
 
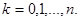
В других примеров приделы вероятностей 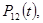  при при 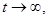 очевидно, не существуют. очевидно, не существуют.
Найдем стационарное распределение в примере 1. Нужно найти вектор 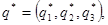 удовлетворяющий условиям (8): удовлетворяющий условиям (8):
  , ,
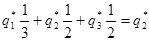 , ,
 ; ;
  
Отсюда,   Таким образом, стационарное распределение существует, но не все координаты векторы Таким образом, стационарное распределение существует, но не все координаты векторы  положительны. положительны.
Для полиномиальной схемы были введены случайные величины, равные чесу исходов данного типа. Введем аналогичные величины для цепей Маркова. Пусть  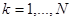 − число попадания системы в состояние − число попадания системы в состояние 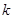 за время за время  . Тогда . Тогда  частота попаданий системы в состояние частота попаданий системы в состояние 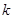 . Используя формулы (9), можно доказать, что . Используя формулы (9), можно доказать, что 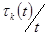 при при 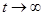 сближается с сближается с  . Для этого нужно получить асимптотические формулы для . Для этого нужно получить асимптотические формулы для 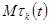 и и  и воспользоваться неравенством Чебышева. Приведем вывод формулы для и воспользоваться неравенством Чебышева. Приведем вывод формулы для  . Представим . Представим 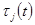 в виде в виде
 (10) (10)
где  , если , если  , и , и 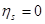 в противном случае. Так как в противном случае. Так как
 , ,
то, воспользовавшись свойством математического ожидания и формулой (9), получим
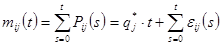 . .
Втрое слагаемое в правой части этого равенства в силу теоремы 1 является частной суммой сходящегося ряда. Положив  , получим , получим
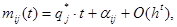 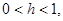 (11) (11)
Поскольку
 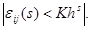
Из формулы (11), в частности, следует, что
 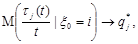 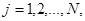 при при 
Так же можно получить формулу для  которая используется для вычисления дисперсии. которая используется для вычисления дисперсии.
§5. Доказательство теоремы о предельных вероятностях в цепи Маркова
Докажем сначала две леммы. Положим
 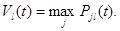
Лемма 1.
При любых 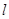 существуют пределы существуют пределы
  и и  
Доказательство. Используя уравнение (3) с  получим получим

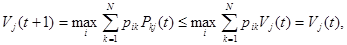
Таким образом, последовательности  и и  монотонны и ограничены. Отсюда следует утверждение леммы 1. монотонны и ограничены. Отсюда следует утверждение леммы 1.
Лемма 2.
Если выполнены условия теоремы 2, то существуют постоянные 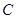 , , 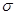  такие, что такие, что
 
Для любых 
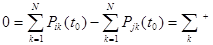 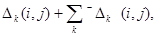
где  , ,  означает суммирование по всем означает суммирование по всем 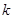 , при которых , при которых  положительно, а положительно, а 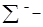 суммирование по остальным суммирование по остальным 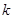 . Отсюда . Отсюда
 . (12) . (12)
Так как в условиях теоремы 1 вероятности перехода  при всех при всех  , то при любых , то при любых 
 (13) (13)
И в силу конечности числа состояний
 (14) (14)
Оценим теперь разность  . Используя уравнение (3) с . Используя уравнение (3) с  , , 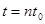 , получим , получим

=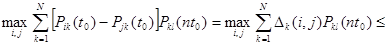
 . .
Отсюда, используя (8)-(10), найдем
 
=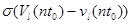 . .
Объединяя это соотношение с неравенством (14) , получим утверждение леммы.
Перейти к доказательству теоремы. Так как последовательности 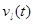 , ,  монотонны, то монотонны, то
0<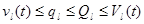 . (15) . (15)
Отсюда и из леммы 1 находим

Следовательно, при  получи получи 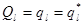 и и
 (16) (16)
Положительность  следует из неравенства (15). Переходя к пределу при следует из неравенства (15). Переходя к пределу при 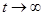 и и  в уравнении (3), получим, что в уравнении (3), получим, что  удовлетворяет уравнению (12). Теорема доказана. удовлетворяет уравнению (12). Теорема доказана.
§6. Области применения цепей Маркова
Цепи Маркова служат хорошим введением в теорию случайных процессов, т.е. теорию простых последовательностей семейства случайных величин, обычно зависящих от параметра, который в большинстве приложений играет роль времени. Она предназначена, главным образом, для полного описания как долговременного, так и локального поведения процесса. Приведем некоторые наиболее изученные в этом плане вопросы.
Броуновское движение и его обобщения - диффузионные процессы и процессы с независимыми приращениями.
Теория случайных процессов способствовала углублению связи между теорией вероятностей, теорией операторов и теорией дифференциальных уравнений, что, помимо прочего, имело важное значение для физики и других приложений. К числу приложений относятся процессы, представляющие интерес для актуарной (страховой) математики, теории массового обслуживания, генетики, регулирования дорожного движения, теории электрических цепей, а также теории учета и накопления товаров.
Мартингалы.
Эти процессы сохраняют достаточно свойств цепей Маркова, чтобы для них оставались в силе важные эргодические теоремы. От цепей Маркова мартингалы отличаются тем, что когда текущее состояние известно, только математическое ожидание будущего, но необязательно само распределение вероятностей, не зависит от прошлого. Помимо того, что теория мартингалов представляет собой важный инструмент для исследования, она обогатила новыми предельными теоремами теорию случайных процессов, возникающих в статистике, теории деления атомного ядра, генетике и теории информации.
Стационарные процессы.
Самая старая из известных эргодических теорем, как отмечалось выше, может быть интерпретирована как результат, описывающий предельное поведение стационарного случайного процесса. Такой процесс обладает тем свойством, что все вероятностные законы, которым он удовлетворяет, остаются инвариантными относительно сдвигов по времени. Эргодическую теорему, впервые сформулированную физиками в качестве гипотезы, можно представить как утверждение о том, что при определенных условиях среднее по ансамблю совпадает со средним по времени. Это означает, что одну и ту же информацию можно получить из долговременного наблюдения за системой и из одновременного (и одномоментного) наблюдения многих независимых копий той же самой системы. Закон больших чисел есть не что иное, как частный случай эргодической теоремы Биркгофа. Интерполяция и предсказание поведения стационарных гауссовских процессов, понимаемых в широком смысле, служат важным обобщением классической теории наименьших квадратов. Теория стационарных процессов - необходимое орудие исследования во многих областях, например, в теории связи, которая занимается изучением и созданием систем, передающих сообщения при наличии шума или случайных помех.
Марковские процессы (процессы без последействия) играют огромную роль в моделировании систем массового обслуживания (СМО), а также в моделировании и выборе стратегии управления социально-экономическими процессами, происходящими в обществе.
Также цепь Маркова можно использовать для генерации текстов. На вход подается несколько текстов, затем строится цепь Маркова с вероятностями следования одних слов за другими и на основе данной цепи создается результирующий текст. Игрушка получается весьма занятной!
Заключение
Таким образом, в нашей курсовой работе речь шла о схеме цепей Маркова. Узнали, в каких областях и как она применяется, независимые испытания являются доказали теорему о предельных вероятностях в цепи Маркова, приводили примеры для типичной и однородной цепи Маркова, а так же для нахождения матрицы перехода.
Мы убедились в том, что схема цепей Маркова является непосредственным обобщением схемы независимых испытаний.
Список использованной литературы
1. Чистяков В.П. Курс теории вероятностей. 6-е изд., испр. − СПб.: Издательство «Лань», 2003. − 272 с. − (Учебник для вузов. Специальная литература).
2. Гнеденко Б.В. Курс теории вероятностей.
3. Гмурман В.Е. Теория вероятностей и математическая статистика.
4. Вентцель Е.С. Теория вероятностей и ее инженерные приложения.
5. Колмогоров А.Н., Журбенко И.Г., Прохоров А.В. Введение в теорию вероятностей. − Москва-Ижевск: Институт компьютерных исследований, 2003, 188 стр.
6. Кац М. Вероятность и смежные вопросы в физике.
|