Министерство образования Российской Федерации
Архангельский государственный технический университет
Факультет промышленной энергетики ПТЭIII-2
Кафедра теплотехники
Реферат
Распределение температуры по сечению балки.
Руководитель работы: С.И. Осташев
Студент Шафоростов А.В.
Архангельск
2009
Содержание
Задание
Расчет распределения температуры по сечению балки явным методом
Расчет распределения температуры по сечению балки неявным методом
Список литературы
Необходимо нагреть груз прямоугольного сечения. Теплота с помощью нагревателя подводится с одной из сторон. Нагреватель должен работать до тех пор, пока температура противоположной стороны не достигнет заданного значения Tk
. Первоначально груз имел температуру Tн
. Остальные 3 поверхности окружены воздухом с температурой T∞.
Коэффициент теплоотдачи от этих поверхностей α. Температура нагревания TS
.
Сколько времени должен работать нагреватель, чтобы минимальная температура на противоположной стороне бруса составила Tк
. Расчёты выполнить явным и неявным методом.

распределение температура сечение балка
Методика численного решения задач нестационарной теплопроводности аналогична рассмотренной методике решения задач стационарной теплопроводности. При решении нестационарных задач для каждого узла необходимо дополнительно учесть аккумулирование энергии - в материале, величина которой определяется теплофизическими свойствами материала. Принцип метода заключается в определении температуры в узле в момент времени τ+Δτ, зная температуру в этом узле и в соседних узлах в предыдущий момент времени τ, поэтому этот метод и называется явным.
Чтобы решить задачу нестационарной теплопроводности численным методом необходимо знать начальное распределение температуры в твердом теле (временные граничные условия). Обычно в качестве такого условия тело рассматривают изотермичным, а температуры во всех узлах - равными начальной температуре тела. Затем, после расчета всех температур в момент времени Δτ процесс повторяют и рассчитывают температур в момент времени 2Δτ. Эту процедуру повторяют до тех пор, пока не будет достигнут момент времени, для которого требуется знать распределение температуры.
Следует также иметь в виду,что для выделения единственности решения дифференциального уравнения в частных производных вводят дополнительные условия, при этом:
1. для избежания противоречивости в условиях постановки задачи убеждаются в решении данной задачи при рассматриваемых условиях путем доказательства теоремы существования решения.
2. для исключения получения бесчисленного множества решений также убеждаются в единственности решения при рассматриваемых условиях путем доказательства теоремы о единственности решения.
3. для исключения противоречивости решения проверяют задачу на устойчивость. Устойчивой называется задача математической физики, в которой при достаточно малом изменении аргумента наблюдается сколь угодно малое изменение решения. Из изложенного следует, что в данном методе выбор расстояния между узламиΔxи временного интервала Δτ не является произвольным. В противном случае решение не будет устойчивым, а следовательно можно получить результаты, противоречащие основным законам термодинамики.
Явные разностные уравнения баланса и критерии устойчивости для десяти узлов поверхности балки имеют следующий вид:
















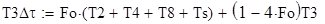
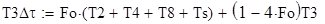


где Bi=α·Δx/λ - число Био, где a - коэффициент теплоотдачи от среды к омываемой поверхности, Вт/ (м К);
Δх - шаг по пространству, м;
λ - коэффициент теплопроводности материала стенки, Вт/ (м-К);
Принимаю Δх=0,05 м (см. рис.1), тогда критерий: Био Bi=84·0,05/69,2=0,06069. Принимаю Δτ=5,248с, тогда критерий Фурье: Fo=69,2·5,248/ (0,052
·465·7860) =0,03974. Условие устойчивости, удовлетворяющее всем десяти уравнениям: Fo (l+Bi) <0,25 Проверяем условие устойчивости: 0,03974· (1+0,06069) = 0,04216<0,25
Условие выполняется, решаем уравнения.
Распределение температуры по сечению балки
.
| Время |
Температура, град С, в узле |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 0 |
54 |
54 |
54 |
54 |
54 |
54 |
54 |
54 |
54 |
54 |
| 5,248 |
72,367 |
72,521 |
72,521 |
72,521 |
72,367 |
53,691 |
53,846 |
53,846 |
53,846 |
53,691 |
| 10,5 |
89,185 |
89,558 |
89,564 |
89,558 |
89,185 |
54,882 |
55,17 |
55,177 |
55,17 |
54,882 |
| 15,74 |
104,65 |
105,28 |
105,3 |
105,28 |
104,65 |
57,315 |
57,733 |
57,749 |
57,733 |
57,315 |
| 20,99 |
118,93 |
119,85 |
119,9 |
119,85 |
118,93 |
60,77 |
61,324 |
61,356 |
61,324 |
60,77 |
| 26,24 |
132,16 |
133,4 |
133,47 |
133,4 |
132,16 |
65,063 |
65,766 |
65,817 |
65,766 |
65,063 |
| 31,49 |
144,48 |
146,03 |
146,14 |
146,03 |
144,48 |
70,037 |
70,905 |
70,979 |
70,905 |
70,037 |
| 36,74 |
155,98 |
157,85 |
158 |
157,85 |
155,98 |
75,56 |
76,609 |
76,711 |
76,609 |
75,56 |
| 41,98 |
166,75 |
168,94 |
169,14 |
168,94 |
166,75 |
81,519 |
82,766 |
82,901 |
82,766 |
81,519 |
| 47,23 |
176,88 |
179,39 |
179,65 |
179,39 |
176,88 |
87,819 |
89,279 |
89,452 |
89,279 |
87,819 |
| 52,48 |
186,43 |
189,26 |
189,57 |
189,26 |
186,43 |
94,379 |
96,066 |
96,282 |
96,066 |
94,379 |
| 57,73 |
195,46 |
198,6 |
198,97 |
198,6 |
195,46 |
101,13 |
103,06 |
103,32 |
103,06 |
101,13 |
| 62,98 |
204,02 |
207,47 |
207,9 |
207,47 |
204,02 |
108,02 |
110,2 |
110,51 |
110,2 |
108,02 |
| 68,22 |
212,16 |
215,9 |
216,4 |
215,9 |
212,16 |
114,99 |
117,43 |
117,8 |
117,43 |
114,99 |
| 73,47 |
219,91 |
223,95 |
224,51 |
223,95 |
219,91 |
122,01 |
124,71 |
125,15 |
124,71 |
122,01 |
| 78,72 |
227,32 |
231,63 |
232,26 |
231,63 |
227,32 |
129,05 |
132,02 |
132,51 |
132,02 |
129,05 |
| 83,97 |
234,4 |
238,99 |
239,68 |
238,99 |
234,4 |
136,06 |
139,31 |
139,87 |
139,31 |
136,06 |
| 89,22 |
241,18 |
246,04 |
246,8 |
246,04 |
241,18 |
143,03 |
146,56 |
147, 19 |
146,56 |
143,03 |
| 94,46 |
247,69 |
252,81 |
253,64 |
252,81 |
247,69 |
149,95 |
153,75 |
154,45 |
153,75 |
149,95 |
| 99,71 |
253,95 |
259,32 |
260,22 |
259,32 |
253,95 |
156,79 |
160,86 |
161,64 |
160,86 |
156,79 |
| 105 |
259,97 |
265,59 |
266,55 |
265,59 |
259,97 |
163,53 |
167,89 |
168,74 |
167,89 |
163,53 |
| 110,2 |
265,77 |
271,63 |
272,66 |
271,63 |
265,77 |
170,18 |
174,81 |
175,74 |
174,81 |
170,18 |
| 115,5 |
271,36 |
277,47 |
278,56 |
277,47 |
271,36 |
176,72 |
181,62 |
182,63 |
181,62 |
176,72 |
| 120,7 |
276,77 |
283,1 |
284,26 |
283,1 |
276,77 |
183,14 |
188,32 |
189,4 |
188,32 |
183,14 |

И так из результатов расчёта явным методом следует, что следует работать 73,47 сек, чтобы минимальная температура на противоположной стороне балки (узлы 6 и 10) была равна Tк
=122˚С.
Основной недостаток явного численного метода состоит в том, что разностные уравнения баланса энергии для каждого узла должны удовлетворять критерию устойчивости. Чтобы удовлетворять критерию устойчивости в практике приходится выбирать очень маленький шаг по времени, и это приводит к значительному возрастанию объёма расчётов. Рассмотрим другой метод, который является устойчивым при любых значениях чисел Biи Fo. Суть его заключается в том, что уравнение баланса, полученное для явного метода, модифицирует, выражая через температуру в момент времени τ+Δτ. В этом методе разностные уравнения необходимо записывать для всех узлов, поэтому метод получил название неявного. Данный метод в математике называют методом использования левых производных, т.к. производная по времени опраксимируется разностью. Очевидно, что существенное преимущество неявного метода - это отсутствие критериев устойчивости, а недостаток - необходимость решения системы алгебраических уравнений (в отличие от неявного метода в явном можно решать разностные уравнения отдельно для каждого узла).
1. (1+2Fo· (2+Bi)) · (T1
) τ+
Δτ
-2·Fo· (1/2· (T6
) τ+
Δτ
+ (T2
) τ+
Δτ
+ Bi·T∞
+ 1/2·Ts
) - (T1
) τ
=0
2. (1+4Fo) · (T2
) τ+
Δτ
- Fo· ( (T1
) τ+
Δτ
+ (T3
) τ+
Δτ
+ (T7
) τ+
Δτ
+ Ts
) - (T2
) τ
=0
3. (1+4Fo) · (T3
) τ+
Δτ
- Fo· ( (T2
) τ+
Δτ
+ (T4
) τ+
Δτ
+ (T8
) τ+
Δτ
+ Ts
) - (T3
) τ
=0
4. (1+4Fo) · (T4
) τ+
Δτ
- Fo· ( (T3
) τ+
Δτ
+ (T5
) τ+
Δτ
+ (T9
) τ+
Δτ
+ Ts
) - (T4
) τ
=0
5. (1+2Fo· (2+Bi)) · (T5
) τ+
Δτ
-2·Fo· (1/2· (T10
) τ+
Δτ
+ (T4
) τ+
Δτ
+ Bi·T∞
+ 1/2·Ts
) - (T5
) τ
=0
6. (1+4Fo· (1+Bi)) · (T6
) τ+
Δτ -
4·Fo· (1/2· (T1
) τ+
Δτ
+ 1/2· (T7
) τ+
Δτ
+ Bi·T∞
) - (T6
) τ
=0
7. (1+2Fo· (2+Bi)) · (T7
) τ+
Δτ
-2·Fo· (1/2· (T6
) τ+
Δτ
+1/2· (T8
) τ+
Δτ
+Bi·T∞
+ (T2
) τ+
Δτ
) - (T7
) τ
=0
8. (1+2Fo· (2+Bi)) · (T8
) τ+
Δτ
-2·Fo· (1/2· (T7
) τ+
Δτ
+1/2· (T9
) τ+
Δτ
+Bi·T∞
+ (T3
) τ+
Δτ
) - (T8
) τ
=0
9. (1+2Fo· (2+Bi)) · (T9
) τ+
Δτ
-2·Fo· (1/2· (T8
) τ+
Δτ
+1/2· (T10
) τ+
Δτ
+Bi·T∞
+ (T4
) τ+
Δτ
) - (T9
) τ
=0
10. (1+4Fo· (1+Bi)) · (T10
) τ+
Δτ -
4·Fo· (1/2· (T5
) τ+
Δτ
+ 1/2· (T9
) τ+
Δτ
+ Bi·T∞
) - (T10
) τ
=0
1.95-0.460.000.000.00-0.230.000.000.000.00 120,21
0.231.92-0.230.000.000.00-0.230.000.000.00 119,6
0.00-0.231.92-0.230.000.000.00-0.230.000.00 119,6
0.000.00-0.231.92-0.230.000.000.00-0.230.00 119,6
0.000.000.00-0.461.950.000.000.000.00-0.23 120,21
0.460.000.000.000.001.98-0.460.000.000.00 1,23
0.00-0.460.000.000.00-0.231.95-0.230.000.00 0,61
0.000.00-0.460.000.000.00-0.231.95-0.230.00 0,61
0.000.000.00-0.460.000.000.00-0.231.95-0.23 0,61
0.000.000.000.00-0.460.000.000.00-0.461.98 1,23
шаг по пространству - 0.05
шаг по времени - 30.00
начальная температура - 54.0
Распределение температуры по сечению балки
| Время |
Температура, град С, в узле |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 0 |
54 |
54 |
54 |
54 |
54 |
54 |
54 |
54 |
54 |
54 |
| 30 |
129,13 |
130,78 |
130,98 |
130,78 |
129,13 |
75,75 |
76,88 |
77,04 |
76,88 |
75,75 |
| 60 |
184,96 |
188,34 |
188,84 |
188,34 |
184,96 |
107,37 |
109,88 |
110,28 |
109,88 |
107,37 |
| 90 |
228,22 |
233,21 |
234,06 |
233,21 |
228,22 |
141,71 |
145,64 |
146,44 |
145,64 |
141,71 |
| 120 |
262,88 |
269,29 |
270,5 |
269,29 |
262,88 |
175,23 |
180,64 |
181,83 |
180,64 |
175,23 |
| 150 |
291,32 |
298,98 |
300,53 |
298,98 |
291,32 |
206,32 |
213,14 |
214,73 |
213,14 |
206,32 |
| 180 |
315,07 |
323,81 |
325,68 |
323,81 |
315,07 |
234,35 |
242,48 |
244,46 |
242,48 |
234,35 |
| 210 |
335,14 |
344,82 |
346,98 |
344,82 |
335,14 |
259,23 |
268,53 |
270,87 |
268,53 |
259,23 |
| 240 |
352,23 |
362,73 |
365,15 |
362,73 |
352,23 |
281,08 |
291,43 |
294,11 |
291,43 |
281,08 |
| 270 |
366,87 |
378,08 |
380,72 |
378,08 |
366,87 |
300,17 |
311,44 |
314,42 |
311,44 |
300,17 |
| 300 |
379,45 |
391,27 |
394,11 |
391,27 |
379,45 |
316,78 |
328,86 |
332,1 |
328,86 |
316,78 |
| 330 |
390,28 |
402,63 |
405,64 |
402,63 |
390,28 |
331,2 |
343,98 |
347,45 |
343,98 |
331,2 |
| 360 |
399,62 |
412,43 |
415,59 |
412,43 |
399,62 |
343,69 |
357,1 |
360,77 |
357,1 |
343,69 |

И так из результатов расчёта неявным методом следует, что следует работать 73,47 сек, чтобы минимальная температура на противоположной стороне балки (узлы 6 и 10) была равна Tк
=122˚С.
1. Лекции “Моделирование процессов теплообмена”.
|