Содержание
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Список используемой литературы
Задание 1
Построить таблицу значений функции алгебры логики, найти все существенные переменные: 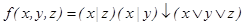
Решение
Распишем данную функцию по действиям и для всех наборов значений 3 переменных, посчитаем их результаты:
| xyz
|
x|z
|
x|y
|
x V y V z
|
(x|z)( x|y)
|
f
|
| 000 |
1 |
1 |
0 |
1 |
0 |
| 001 |
1 |
1 |
1 |
1 |
0 |
| 010 |
1 |
1 |
1 |
1 |
0 |
| 011 |
1 |
1 |
1 |
1 |
0 |
| 100 |
1 |
1 |
1 |
1 |
0 |
| 101 |
0 |
1 |
1 |
0 |
0 |
| 110 |
1 |
0 |
1 |
0 |
0 |
| 111 |
0 |
0 |
1 |
0 |
0 |
Функция тождественно принимает значение 0 при любых значениях переменных x,y,z. Поэтому в данной функции существенных переменных нет.
Задание 2
Построить полином Жегалкина функции:
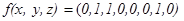
Решение
Записываем таблицу значений функции
| xyz |
f |
| 000 |
0 |
| 001 |
1 |
| 010 |
1 |
| 011 |
0 |
| 100 |
0 |
| 101 |
0 |
| 110 |
1 |
| 111 |
0 |
Находим СДНФ функции по единицам:
СДНФ функции: 
Полином Жегалкина:
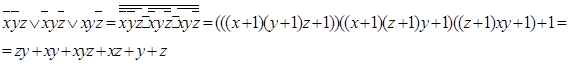
Задание 3
Найти СКНФ и СДНФ функции:
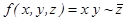
Решение
Найдем с помощью таблицы значений:
| xyz |
xy |
 |
f |
| 000 |
0 |
1 |
0 |
| 001 |
0 |
0 |
1 |
| 010 |
0 |
1 |
0 |
| 011 |
0 |
0 |
1 |
| 100 |
0 |
1 |
0 |
| 101 |
0 |
0 |
1 |
| 110 |
1 |
1 |
1 |
| 111 |
1 |
0 |
0 |
Получим СДНФ (единицы функции) и СКНФ (нули функции):
СДНФ (единицы): 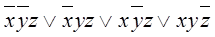
СКНФ (нули): 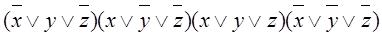
Задание 4
С помощью карт Карно найти минимальную КНФ и ДНФ функции:

Решение
Запишем карту Карно:
| zt |
00 |
01 |
11 |
10 |
| xy |
| 00 |
1 |
1 |
0 |
0 |
| 01 |
1 |
0 |
0 |
0 |
| 11 |
1 |
0 |
0 |
1 |
| 10 |
0 |
0 |
1 |
0 |
Минимальные формы:
КНФ (покрытия по нулям): 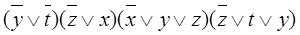
ДНФ (покрытия по единицам): 
Задание 5
Придумать связный ориентированный граф из пяти вершин и не менее чем семи ребер (ориентированы могут быть не все ребра). Для данного графа составить структурную матрицу, по ней (методами булевой алгебры) найти все пути и сечения между двумя любыми несмежными вершинами на ваш выбор
Решение
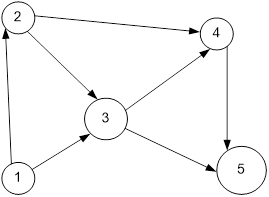
Таблица:
| 1 |
2 |
3 |
4 |
5 |
| 1 |
0 |
1 |
1 |
0 |
0 |
| 2 |
0 |
0 |
1 |
1 |
0 |
| 3 |
0 |
0 |
0 |
1 |
1 |
| 4 |
0 |
0 |
0 |
0 |
1 |
| 5 |
0 |
0 |
0 |
0 |
0 |
Пути из 1 в 4:
1. 1-3-4
2. 1-2-4
Задание 6
Придумать связный взвешенный граф из восьми вершин и не менее чем 14 ребер (нумерация ребер – слева направо, веса от 1 до 20). Для этого графа построить минимально островное дерево с помощью алгоритма Прима, и найти расстояние между вершинами 1 и 8 с помощью алгоритма Дейкстры. Реализовать алгоритм на любом языке программирования.
алгебра логика графполином дейкстра
Решение
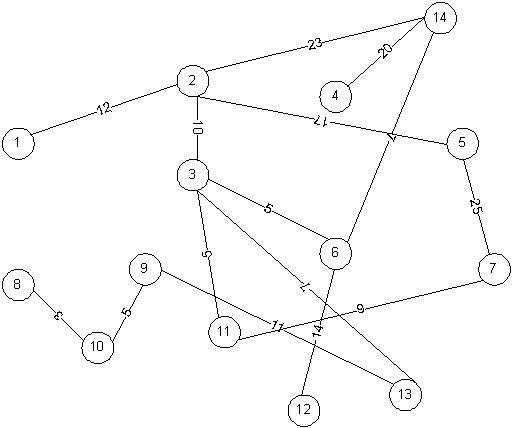
Текст программы для алгоритма Дейкстра
//---------------------------------------------------------------------------
#include <clx.h>
#pragma hdrstop
//---------------------------------------------------------------------------
#pragma argsused
//Нахождение расстояния от источника до всех вершин в графе
//с неотрицательными весами (метод Дейкстры).
//Нахождение кратчайшего пути из S в T.
#include <iostream.h>
#define MaxNodes 14
#define B 1000 //Машинный эквивалент бесконечности.
//Описание типа узла стека.
typedef struct Zveno *svqz;
struct Zveno
{
int Element;
svqz Sled;
};
class Spisok
{
private:
int A[MaxNodes][MaxNodes]; //Матрицавесовдуг.
int D[MaxNodes]; //Матрица расстояний от источника до
//всех вершин графа.
svqz Stack; //Указатель на рабочий стек.
void UDALENIE (svqz *, int *);
void W_S (svqz *, int);
int Pusto_Q (int *);
public:
Spisok() {Stack = NULL;}
void Vvod_Ves();
void Reshenie ();
};
void main ()
{
Spisok A;
A.Vvod_Ves();
A.Reshenie();
}
int Spisok::Pusto_Q (int *Q)
{
for (int i=0;i<MaxNodes;i++)
if ( *(Q+i)!=0 ) return 0; //Ложь - непусто!
return 1; //Истина - пусто!
}
void Spisok::Reshenie ()
{
int S; // Начальная вершина пути (источник).
int T; // Конечная вершина пути.
int u,v,Min;
int i,j,k;
svqz UkZv;
int Q[MaxNodes];
cout << "input source : ";
cin >> S; S--;
//Инициализация.
for (i=0;i<MaxNodes;i++) { D[i] = A[S][i]; Q[i] = 0; }
D[S] = 0;
for (i=0;i<MaxNodes;i++) Q[i] = 1;
Q[S] = 0;
//Вычисление матрицы расстояний от
//источника до всех вершин графа.
while (!Pusto_Q(&Q[0])) //Пока Q не пусто.
{
Min = B;
for (i=0;i<MaxNodes;i++)
if (Q[i]==1 && D[i]<Min) { Min = D[i]; u = i; }
Q[u] = 0;
for (i=0;i<MaxNodes;i++)
if (Q[i] == 1)
if ( D[i] > D[u]+A[u][i] ) D[i] = D[u] + A[u][i];
}
//Вывод матрицы расстояний от источника
//до всех вершин графа.
cout << "matrix of distanses: \n";
for (i=0;i<MaxNodes;i++) cout << D[i] << " ";
cout << endl;
// -----------------------------------------------------
// Нахождение кратчайшего пути из S в T с использованием
// построенной матрицы расстояний.
// -----------------------------------------------------
cout << "Inpute finish node: ";
cin >> T; T--;
W_S (&Stack,T); v = T;
while ( v!=S )
{
for (i=0;i<MaxNodes;i++)
if ( D[v]==D[i]+A[i][v] ) u = i;
W_S (&Stack,u);
v = u;
}
//Вывод кратчайшего пути на экран дисплея.
cout << "Minimal path: ";
UkZv = Stack;
while ( UkZv != NULL )
{ cout << (UkZv->Element+1) << " ";
UkZv = UkZv->Sled; }
cout << endl;
}
void Spisok::Vvod_Ves()
//Вводматрицывесовдугзаданногографа.
{
cout << "Inppute the elements of edge matrix by strings:\n";
for (int i=0;i<MaxNodes;i++)
for (int j=0;j<MaxNodes;j++)
{
cout << "Inpute A[" << (i+1) << "," << (j+1) << "]: ";
cin >> A[i][j];
if ( A[i][j]==0 ) A[i][j] = B;
}
}
void Spisok::W_S (svqz *stk, int Elem)
//Помещение Elem в стек stk.
{
svqz q=new (Zveno);
(*q).Element = Elem;
(*q).Sled = *stk; *stk = q;
}
void Spisok::UDALENIE (svqz *stk, int *Klad)
//Удаление звена из стека, заданного указателем *stk.
//Значение информационного поля удаляемого звена сохраня-
//ется в параметре Klad.
{
svqz q;
if (*stk==NULL) cout<<"try to select from the empty stack!\n";
else
{ *Klad = (**stk).Element;
q = *stk; *stk = (**stk).Sled; delete q; }
}
АлгоритмПрима://---------------------------------------------------------------------------
#include <clx.h>
#pragma hdrstop
//---------------------------------------------------------------------------
#pragma argsused
#include <iostream.h>
#define TRUE 1
#define FALSE 0
typedef int Boolean;
typedef unsigned int SubInt;
typedef struct Uzel *Ref;
struct Uzel
{
SubInt X; //Началодуги.
SubInt Y; //Конец дуги
int Pay; //Стоимость дуги.
Ref Left; //Указатель на левого сына.
Ref Right;//Указатель на правого сына.
};
typedef struct zveno *svqz;
struct zveno
{
unsigned int Element[256];
svqz Sled;
zveno();
};
zveno::zveno()
{
for(int k=0;k<256;Element[k++]=0);
}
class Spisok
{
private:
Ref Root;
void Search (int, int, int, Ref *);
void Poisk (svqz, SubInt, svqz *);
void Postroenie (svqz *);
void Udalenie (svqz *, svqz);
public:
Spisok() { Root = NULL;} //Вначаледеревопусто.
void Reshenie();
void Postr();
};
void Spisok::Search (int A, int B, int C, Ref *p)
//Добавление вершины, содержащей поля A,B,C, в дерево *p.
{
if ( (*p) == NULL )
{
(*p) = new (Uzel); (**p).X = A; (**p).Y = B; (**p).Pay = C;
(**p).Left = (**p).Right = NULL;
}
else
if ( C<=(**p).Pay ) Search (A,B,C,&((**p).Left));
else
if ( C>(**p).Pay ) Search (A,B,C,&((**p).Right));
}
void Spisok::Postroenie (svqz *UkStr)
//Постpоение линейного однонапpавленного списка
//с заглавным звеном, содержащего вершины графа.
{
svqz UkZv;
int el;
(*UkStr) = new (zveno);
UkZv = (*UkStr); UkZv->Sled = NULL;
cout << "Input nodes: \n";
cin >> el;
while ( el!=0 )
{
UkZv->Sled = new (zveno); UkZv = UkZv->Sled;
UkZv->Element[el] = 1; UkZv->Sled = NULL;
cin >> el;
}
}
void Spisok::Postr()
//Постpоение деpева, содержащего все ребра графа.
{
int A,B,C;
cout << "For every nodes input input start and finish\n";
cout << "node and cost of edge:\n";
cin >> A >> B >> C;
while ( A!=0 )
{ Search (A,B,C,&Root);
cin >> A >> B >> C;
}
}
void Spisok::Poisk (svqz st, SubInt MENT, svqz *Res)
{
svqz q;
(*Res) = NULL; q = st->Sled;
while ( q != NULL && (*Res) == NULL )
{
if ( q->Element[MENT]==1 ) (*Res) = q;
else q = q->Sled;
}
}
void Spisok::Udalenie (svqz *zv, svqz UkStr)
//Удаление из однонапpавленного списка с заглавным звеном
//элемента, на который указывает указатель zv.
{
svqz Z; //"Стаpый" указатель.
svqz UkZv1; //"Hовый" указатель.
if ( (*zv)->Sled != NULL ) (**zv) = *((**zv).Sled);
else
{ Z = UkStr; UkZv1 = UkStr->Sled;
while (UkZv1 != (*zv))
{ Z = UkZv1; UkZv1 = UkZv1->Sled; }
Z->Sled = NULL; delete UkZv1;
}
}
void Spisok::Reshenie()
{
svqz UkStr; //Указательнасписок.
Ref UkUzel; //Рабочий указатель на узел дерева.
Ref UkUzel1; //Рабочий указатель на узел дерева.
SubInt T1,T2;
svqz Res1,Res2;
//Построение первоначальных множеств вершин графа.
Postroenie (&UkStr);
cout <<"Edges with minimsl cost: ";
while ( UkStr->Sled->Sled != NULL )
{
UkUzel1 = Root; //"Отстающий" указатель.
UkUzel = Root->Left; //"Опережающий" указатель.
if ( UkUzel== NULL )
{ //Выбор в дереве ребра наименьшей стоимости и ...
T1 = Root->X; T2 = Root->Y;
//... удаление этого ребра из дерева.
Root = Root->Right; delete UkUzel1;
}
else
{ //Выбор в дереве ребра наименьшей стоимости и ...
while ( UkUzel->Left != NULL )
{
UkUzel1 = UkUzel1->Left;
UkUzel = UkUzel->Left;
}
T1 = UkUzel->X; T2 = UkUzel->Y;
//... удаление этого ребра из дерева.
UkUzel1->Left = UkUzel->Right;
delete UkUzel;
}
//Если v и w принадлежат различным
//множествам W1 и W2 из VS ...
Res1 = Res2 = NULL;
Poisk (UkStr,T1,&Res1);
Poisk (UkStr,T2,&Res2);
if ( Res1!=Res2 )
{
for (int k=0;k<256;k++)
if ( Res1->Element[k]==1 || Res2->Element[k]==1 )
Res1->Element[k]=1;
Udalenie (&Res2,UkStr);
cout << "(" << T1 << " " << T2 << ") ";
}
}
}
void main ()
{
Spisok Tree;
Tree.Postr();
Tree.Reshenie();
}
Список используемой литературы
1. Нефедов В.Н., Осипова В.А. Курс дискретной математики / МАИ. М., 1992.
2. Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978.
3. Уилсон Р. Введение в теорию графов. М.: Мир, 1977.
4. Берзтисс А.Т.Структуры данных.1974 |