Содержание
1. Введение
2. Теоретическая часть
а) Основные понятия теории графов
б) Понятия смежности, инцидентности, степени
в) Маршруты и пути
г) Матрицы смежности и инцедентности
3. Алгоритм http://hghltd.yandex.com/yandbtm?url=http%3A//www.fos.ru/matemat/9228.html&text=%CF%EE%E8%F1%EA+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE+%EF%F3%F2%E8+%E2+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC+%E3%F0%E0%F4%E5+%2C+%F0%E5%F4%E5%F0%E0%F2&reqtext=%28%CF%EE%E8%F1%EA%3A%3A783+%26+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE%3A%3A22975+%26%26/%28-3+3%29+%EF%F3%F2%E8%3A%3A5309+%26+%E2%3A%3A0+%26+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC%3A%3A42191+%26+%E3%F0%E0%F4%E5%3A%3A31618+%26%26/%28-3+3%29+%F0%E5%F4%E5%F0%E0%F2%3A%3A6724%29//6&dsn=530&d=2003257 - YANDEX_28поиска минимального пути из 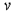 в в 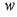 в http://hghltd.yandex.com/yandbtm?url=http%3A//www.fos.ru/matemat/9228.html&text=%CF%EE%E8%F1%EA+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE+%EF%F3%F2%E8+%E2+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC+%E3%F0%E0%F4%E5+%2C+%F0%E5%F4%E5%F0%E0%F2&reqtext=%28%CF%EE%E8%F1%EA%3A%3A783+%26+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE%3A%3A22975+%26%26/%28-3+3%29+%EF%F3%F2%E8%3A%3A5309+%26+%E2%3A%3A0+%26+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC%3A%3A42191+%26+%E3%F0%E0%F4%E5%3A%3A31618+%26%26/%28-3+3%29+%F0%E5%F4%E5%F0%E0%F2%3A%3A6724%29//6&dsn=530&d=2003257 - YANDEX_31ориентированном орграфе (алгоритм фронта волны) в http://hghltd.yandex.com/yandbtm?url=http%3A//www.fos.ru/matemat/9228.html&text=%CF%EE%E8%F1%EA+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE+%EF%F3%F2%E8+%E2+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC+%E3%F0%E0%F4%E5+%2C+%F0%E5%F4%E5%F0%E0%F2&reqtext=%28%CF%EE%E8%F1%EA%3A%3A783+%26+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE%3A%3A22975+%26%26/%28-3+3%29+%EF%F3%F2%E8%3A%3A5309+%26+%E2%3A%3A0+%26+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC%3A%3A42191+%26+%E3%F0%E0%F4%E5%3A%3A31618+%26%26/%28-3+3%29+%F0%E5%F4%E5%F0%E0%F2%3A%3A6724%29//6&dsn=530&d=2003257 - YANDEX_31ориентированном орграфе (алгоритм фронта волны)
4. Листинг программы
5. Примеры выполнения программы
6. Использованная литература
Введение
Развитие теории графов в основном обязано большому числу всевозможных приложений. По-видимому, из всех математических объектов графы занимают одно из первых мест в качестве формальных моделей реальных систем.
Графы нашли применение практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, лингвистике, социальных науках, технике и т.п. Наибольшей популярностью теоретико-графовые модели используются при исследовании коммуникационных сетей, систем информатики, химических и генетических структур, электрических цепей и других систем сетевой структуры.
Благодаря своему широкому применению, теория о нахождении кратчайших путей в последнее время интенсивно развивается.
Нахождение кратчайшего пути - жизненно необходимо и используется практически везде, начиная от нахождения оптимального маршрута между двумя объектами на местности (напр. кратчайший путь от дома до академии),также используется в системах автопилота, используется для нахождения оптимального маршрута при перевозках коммутации информационного пакета Internet и мн. др.
Кратчайший путь рассматривается при помощи графов.
Цель курсовой работы:
Разработать программу поиска оптимального пути в ненагруженном ориентированном графе на любом языке программирования.
Теоретическая часть:
а) Основные понятия теории графов
Теория графов как теоретическая дисциплина может рассматриваться как раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами. Как прикладная дисциплина теория графов позволяет описывать и исследовать многие физические, технические, экономические, биологические, социальные и другие системы. Например, графом, изображенным на рис. 1, в котором точки − вершины графа − города, линии, соединяющие вершины − ребра − дороги, соединяющие города, описывается так называемая транспортная задача (задача нахождения кратчайшего пути из одного города- пункта в другой).
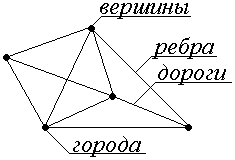
Рис. 1.
Формальное определение графа таково. Пусть задано конечное множество V, состоящее из n элементов, называемых вершинами графа, и подмножество X декартова произведения V×V, то есть 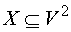 , называемое множеством дуг, тогда ориентированным графом в называется совокупность (V,X). Неориентированным графом G называется совокупность множества V и множества ребер − неупорядоченных пар элементов, каждый из которых принадлежит множеству V. , называемое множеством дуг, тогда ориентированным графом в называется совокупность (V,X). Неориентированным графом G называется совокупность множества V и множества ребер − неупорядоченных пар элементов, каждый из которых принадлежит множеству V.
Одинаковые пары - параллельные или кратные ребра;
Кратностью ребер называют количество одинаковых пар.

Рис.2.
Например, кратность ребра {v1,v2} в графе, изображенном на рис. 2, равна двум, кратность ребра {v3,v4} − трем.
Псевдограф − граф, в котором есть петли и/или кратные ребра.
Мультиграф − псевдограф без петель.
Граф − мультиграф, в котором ни одна пара не встречается более одного раза.
Граф называется ориентированным, если пары (v,w) являются упорядоченными.
Ребра ориентированного графа называются дугами.
Итак, используемые далее обозначения:
V – множество вершин;
X – множество ребер или дуг;
v (или vi)– вершина или номер вершины;
G, G0 - неориентированный граф;
D, D0 – ориентированный;
{v,w} − ребра неориентированного графа;
{v,v} – обозначение петли;
(v,w) − дуги в ориентированном графе;
v,w - вершины, x,y,z – дуги и ребра;
n(G), n(D) количество вершин графа;
m(G) - количество ребер, m(D) - количество дуг.
Примеры
1) Ориентированный граф D=(V, X), V={v1, v2, v3, v4},
X={x1=(v1,v2), x2=(v1,v2), x3=(v2,v2), x4=(v2,v3)}.

Рис. 3.
2) Неориентированный граф G=(V, X), V={v1, v2, v3, v4, v5},
X={x1={v1,v2}, x2={v2,v3}, x3={v2,v4}, x4={v3,v4}}.

Рис. 4.
б) Понятия смежности, инцидентности, степени
Если x={v,w} - ребро, то v и w − концы ребер.
Если x=(v,w) - дуга ориентированного графа, то v − начало, w – конец дуги.
Вершина v и ребро x неориентированного графа (дуга x ориентированного графа) называются инцидентными, если v является концом ребра x (началом или концом дуги x ).
Вершины v, w называются смежными, если {v,w}ÎX.
Степенью вершины v графа G называется число в (v) ребер графа G, инцидентных вершине v.
Вершина графа, имеющая степень 0 называется изолированной, а степень 1 – висячей.
Полустепенью исхода (захода) вершины v ориентированного графа в называется число d+(v) (d-(v)) дуг ориентированного графа D, исходящих из v (заходящих в v).
Следует заметить, что в случае ориентированного псевдографа вклад каждой петли инцидентной вершине v равен 1 как в d+(v), так и в d-(v).
в) Маршруты и пути
Последовательность v1x1v2x2v3...xkvk+1, (где k³1, viÎV, i=1,...,k+1, xiÎX, j=1,...,k), в которой чередуются вершины и ребра (дуги) и для каждого j=1,...,k ребро (дуга) xj имеет вид {vj,vj+1} (для ориентированного графа (vj,vj+1)), называется маршрутом, соединяющим вершины v1 и vk+1 (путем из v1 в vk+1).
Длина маршрута (пути) − число ребер в маршруте (дуг в пути).
г) Матрицы смежности и инцидентности
Пусть D=(V,X) ориентированный граф, V={v1,...,vn}, X={x1,...,xm}.
Матрица смежности ориентированного графа в − квадратная матрица
A(D)=[aij] порядка n, где
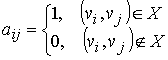
Матрица инцидентности − матрица B(D)=[bij] порядка n´m, где

Матрицей смежности неориентированного графа G=(V,X) называется квадратная симметричная матрица A(G)=[aij] порядка n, где
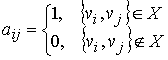 . .
Матрица инцидентности графа G называется матрица B(G)=[bij] порядка n´m, где
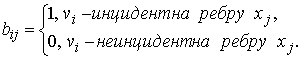
Алгоритм
http://hghltd.yandex.com/yandbtm?url=http%3A//www.fos.ru/matemat/9228.html&text=%CF%EE%E8%F1%EA+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE+%EF%F3%F2%E8+%E2+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC+%E3%F0%E0%F4%E5+%2C+%F0%E5%F4%E5%F0%E0%F2&reqtext=%28%CF%EE%E8%F1%EA%3A%3A783+%26+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE%3A%3A22975+%26%26/%28-3+3%29+%EF%F3%F2%E8%3A%3A5309+%26+%E2%3A%3A0+%26+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC%3A%3A42191+%26+%E3%F0%E0%F4%E5%3A%3A31618+%26%26/%28-3+3%29+%F0%E5%F4%E5%F0%E0%F2%3A%3A6724%29//6&dsn=530&d=2003257 - YANDEX_28поиска минимального пути из 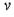 в в 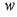 в
http://hghltd.yandex.com/yandbtm?url=http%3A//www.fos.ru/matemat/9228.html&text=%CF%EE%E8%F1%EA+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE+%EF%F3%F2%E8+%E2+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC+%E3%F0%E0%F4%E5+%2C+%F0%E5%F4%E5%F0%E0%F2&reqtext=%28%CF%EE%E8%F1%EA%3A%3A783+%26+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE%3A%3A22975+%26%26/%28-3+3%29+%EF%F3%F2%E8%3A%3A5309+%26+%E2%3A%3A0+%26+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC%3A%3A42191+%26+%E3%F0%E0%F4%E5%3A%3A31618+%26%26/%28-3+3%29+%F0%E5%F4%E5%F0%E0%F2%3A%3A6724%29//6&dsn=530&d=2003257 - YANDEX_31ориентированном орграфе (алгоритм фронта волны) в
http://hghltd.yandex.com/yandbtm?url=http%3A//www.fos.ru/matemat/9228.html&text=%CF%EE%E8%F1%EA+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE+%EF%F3%F2%E8+%E2+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC+%E3%F0%E0%F4%E5+%2C+%F0%E5%F4%E5%F0%E0%F2&reqtext=%28%CF%EE%E8%F1%EA%3A%3A783+%26+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE%3A%3A22975+%26%26/%28-3+3%29+%EF%F3%F2%E8%3A%3A5309+%26+%E2%3A%3A0+%26+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC%3A%3A42191+%26+%E3%F0%E0%F4%E5%3A%3A31618+%26%26/%28-3+3%29+%F0%E5%F4%E5%F0%E0%F2%3A%3A6724%29//6&dsn=530&d=2003257 - YANDEX_31ориентированном орграфе (алгоритм фронта волны)
1) Помечаем вершину 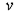 индексом 0, затем помечаем вершины Î образу вершины индексом 0, затем помечаем вершины Î образу вершины 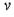 индексом 1. Обозначаем их FW1 (v). Полагаем k=1. индексом 1. Обозначаем их FW1 (v). Полагаем k=1.
2) Если 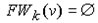 или k=n-1, и одновременно или k=n-1, и одновременно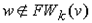 то вершина то вершина 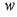 не достижима из не достижима из 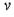 . Работа алгоритма заканчивается. . Работа алгоритма заканчивается.
В противном случае продолжаем:
3) Если 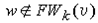 , то переходим к шагу 4. , то переходим к шагу 4.
В противном случае мы нашли минимальный путь из 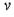 в в 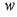 и его длина равна k. Последовательность вершин и его длина равна k. Последовательность вершин
теория орграф матрица алгоритм
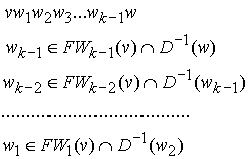
есть этот минимальный путь. Работа завершается.
4) Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин c индексом k. Множество вершин с индексом k+1 обозначаем 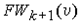 . Присваиваем k:=k+1 и переходим к 2). . Присваиваем k:=k+1 и переходим к 2).
Замечания
Множество 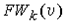 называется фронтом волны kго уровня. называется фронтом волны kго уровня.
Вершины 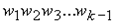 могут быть выделены неоднозначно, что соответствует случаю, если могут быть выделены неоднозначно, что соответствует случаю, если 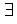 несколько минимальных путей из несколько минимальных путей из 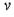 в в 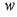 . .
Чтобы найти расстояния в ориентированном графе, необходимо составить матрицу
http://hghltd.yandex.com/yandbtm?url=http%3A//www.fos.ru/matemat/9228.html&text=%CF%EE%E8%F1%EA+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE+%EF%F3%F2%E8+%E2+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC+%E3%F0%E0%F4%E5+%2C+%F0%E5%F4%E5%F0%E0%F2&reqtext=%28%CF%EE%E8%F1%EA%3A%3A783+%26+%EC%E8%ED%E8%EC%E0%EB%FC%ED%EE%E3%EE%3A%3A22975+%26%26/%28-3+3%29+%EF%F3%F2%E8%3A%3A5309+%26+%E2%3A%3A0+%26+%EE%F0%E8%E5%ED%F2%E8%F0%EE%E2%E0%ED%ED%EE%EC%3A%3A42191+%26+%E3%F0%E0%F4%E5%3A%3A31618+%26%26/%28-3+3%29+%F0%E5%F4%E5%F0%E0%F2%3A%3A6724%29//6&dsn=530&d=2003257 - YANDEX_34
минимальных расстояний R(D)между его вершинами. Это квадратная матрица размерности 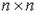 , элементы главной диагонали которой равны нулю ( , элементы главной диагонали которой равны нулю (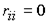 , i=1,..,n). , i=1,..,n).
Сначала составляем матрицу смежности. Затем переносим единицы из матрицы смежности в матрицу минимальных расстояний (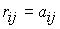 , если , если 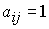 ). Далее построчно заполняем матрицу следующим образом. ). Далее построчно заполняем матрицу следующим образом.
Рассматриваем первую строку, в которой есть единицы. Пусть это строка − i-тая и на пересечении с j-тым столбцом стоит единица (то есть 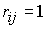 ). Это значит, что из вершины ). Это значит, что из вершины 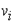 можно попасть в вершину можно попасть в вершину 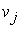 за один шаг. Рассматриваем j-тую сроку (строку стоит вводить в рассмотрение, если она содержит хотя бы одну единицу). Пусть элемент за один шаг. Рассматриваем j-тую сроку (строку стоит вводить в рассмотрение, если она содержит хотя бы одну единицу). Пусть элемент 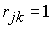 . Тогда из вершины . Тогда из вершины 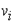 в вершину в вершину 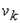 можно попасть за два шага. Таким образом, можно записать можно попасть за два шага. Таким образом, можно записать 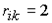 . Следует заметить, что если в рассматриваемых строках две или более единиц, то следует прорабатывать все возможные варианты попадания из одной вершины в другую, записывая в матрицу длину наикратчайшего из них. . Следует заметить, что если в рассматриваемых строках две или более единиц, то следует прорабатывать все возможные варианты попадания из одной вершины в другую, записывая в матрицу длину наикратчайшего из них.
Листинг программы:
#include<stdio.h>
#include<iostream>
using namespace std;
int main()
{
int N=0,n=0,c=0,i=0,k=0;
cout<<" ----------------------------------------------"<<endl;
cout<<" |Poisk optimalnogo puti v nenagrujennom orgrafe|"<<endl;
cout<<" ----------------------------------------------"<<endl;
case1:
cout<<"Vvedite chislo vershin v orgrafe: ";
cin>>N;
if(N<=1)
{
cout<<"Kolichestvo vershin doljno bit'>1!!!"<<endl;
goto case1;
}
///МАТРИЦАсмежности::
cout<<"Zapolnite matricu smejnosti (esli puti net,vvedite 0; esli put' est',vvedite 1):";
float** A = new float*[N];
for(i;i<N;i++)
A[i] = new float[N];
for(i=0;i<N;i++)
for(int k=0;k<N;k++)
{
cout<<"V";
printf("%d",i+1);
cout<<"->V";
printf("%d",k+1);
cout<<'=';
scanf("%f", &A[i][k]);
if((A[i][k]!=0)&&(A[i][k]!=1))
{
cout<<"Vvodite tol'ko 0 ili 1!"<<endl;
return 0;
}
if((i==k)&(A[i][k]==1))
{
cout<<"Na glavnoi diagonali doljni bit' nuli!"<<endl;
return 0;
}
}
////Откуда и куда?(Начальная и конечная вершина в графе!!)
case2:
cout<<"Vvedite nachalnuiu vershinu: ";
cin>>n;
if(n>N)
{
cout<<"Net takoi vershini!"<<endl;
goto case2;
}
if(n==0)
{
cout<<"Net takoi vershini!"<<endl;
goto case2;
}
case3:
cout<<"Vvedite konechnuyu vershinu: ";
cin>>c;
if(c>N)
{
cout<<"Net takoi vershini!"<<endl;
goto case3;
}
if(c==0)
{
cout<<"Net takoi vershini!"<<endl;
goto case3;
}
///Массив,где записывается число шагов
int h=1;
float*B= new float[N];
for(i=0;i<N;i++)
{
B[i]=0;
}
//В массиве B[N-1] ищем вершины,которые достжимы из начала пути
//т.е за один шаг
for(k=0;k<N;k++)
{
if(A[n-1][k]==1)
B[k]=1;
}
//Элементы фронта волны
while(h<50)
{
for(i=0;i<N;i++)
{
for(k=0;k<N;k++)
{
if((B[i]==h)&&(A[i][k]==1)&&(B[k]==0))
B[k]=h+1;
}
}
h++;
}
B[n-1]=0;
if(B[c-1]!=0)
{
///Выводнаэкрантаблицу
cout<<"\nTablica stoimosti minimalnogo puti:"<<endl;
for(i=0;i<N;i++)
{
printf("%f ",B[i]);
}
//Поискобратногопути
cout<<"\n\nOptimal'nii put'(v obratnom poryadke):\n"<<"V";
printf("%d",c);
h=c-1;
int b=B[c-1];
while(b>0)
{
for(i=0;i<N;i++)
if((A[i][h]==1)&&(B[i]==B[h]-1))
{
cout<<"V";
printf("%d",i+1);
h=i;
b--;
}
}
cout<<"\n";
}
else
{
cout<<"\nPuti net!\n";
}
delete A,B;return 0;
}
Примеры выполнения программы:
1.

2.

3.

Использованная литература:
1. «Теория графов». Методические указания по подготовке к контрольным работам по дисциплине «Дискретная математика». Сост.: Н.И. Житникова, Г.И. Федорова, А.К. Галимов. - Уфа, 2005 -37 с.
2. Курс лекций по дискретной математике Житникова В.П.
3. «Самоучитель С++», Перевод с англ. –3 изд.. – СПб.: БХВ-Петербург, 2005 – 688 с.
4. «Дискретная математика для программистов», Ф.А.Новиков.
5. «Введение в дискретную математику», Яблонский.
6. «Курс дискретной математики», Неферов, Осипова.
7. «Информатика» Л.З.Шауцукова.
|